基于GRU神经网络的自相关过程残差控制图

周昊飞

(郑州航空工业管理学院 管理工程学院，河南 郑州 450046)

监控过程波动对于确保过程稳定，提升产品质量水平具有重要意义[1]。控制图作为统计过程控制(statistical process control，SPC)中的有效工具，已被广泛应用于工业过程监控与诊断[2-3]。然而，随着物联网、无线传感等技术的迅猛发展，数据采集的速率越来越高，许多工业自动化生产过程中的数据通常具有强相关性[4]。然而，这些强相关数据流通常并不符合数据独立性的统计假设，直接应用常规休哈特控制图对其进行监控会产生较多的漏判和误判，引起无效的停机排查等问题，进而增加生产成本[5]。因此，如何构造合适的控制图对自相关过程进行监控是当前制造型企业亟待解决的现实问题。

目前，有关自相关过程监控的研究主要集中于基于时间序列模型的控制图[6]、基于机器学习的过程监控[7]等方面。基于时间序列模型的控制图主要是使用时间序列模型对观测数据进行拟合，而后运用常规控制图对形成的残差数据序列进行监控。孙静[8]使用一阶自回归AR (1)模型对实际观测值进行拟合，而后采用休哈特控制图对形成的残差进行监控，建立残差控制图来解决自相关过程的监控问题。Alshraideh等[9]采用时间序列模型中的隐马尔可夫模型 (hidden Markov model，HMM)获取监控变量的残差，而后采用残差控制图对自相关过程进行监控。Albarracin 等[10]采用广义自回归移动平均 (generalized autoregressive integrated moving average，GARMA)模型构建残差累计和控制图对计数时间序列数据进行监控。肖艳等[11]针对多阶自相关的问题，运用蒙特卡洛仿真方法，研究不同自回归阶数的自回归模型对残差控制图性能的影响。上述研究需要对过程变量数据序列选取出一个严格的时间序列模型，对过程数据拟合的限制性假设较多，要求质量人员应当具备较强的数据分析专业能力。基于机器学习的监控方法直接从过程数据中学习得到某些特定的非线性关系，进而对未知的过程数据进行分类或预测，解决上述方法中限制性假设多，应用不灵活等问题[12-13]。White等[14]利用支持向量回归对自相关过程数据预测，而后应用累计和控制图对实测值与预测值的残差进行监控，构建了基于支持向量回归的累计和控制图。Issam等[15]在存在自相关的情况下，比较人工神经网络、自回归综合移动平均ARIMA和支持向量回归模型3种方法的预测性能。上述这些研究主要是应用抗干扰能力强、预测精度高的机器学习算法来形成更具区分力的残差数据序列，进而提升自相关控制图的监控能力。因此，引入具有更强数据学习能力的机器学习方法是进一步提升自相关控制图监控效率的关键问题。

近年来，深度学习的相关算法在自相关过程监控中得以应用。Chen等[16]采用深度学习的循环神经网络 (recurrent neural network，RNN)对自相关过程数据进行预测，构建基于RNN的残差控制图，取得良好的监控效果。RNN纳入序列相关，在学习过程中包含先前时间序列的所有历史信息，是一种处理时间序列数据的神经网络。但是，标准RNN结构在训练过程中存在梯度消失或者爆炸等问题，难以对序列长期依赖关系进行有效的学习[17]。然而，由长短期记忆网络 (long short term memory, LSTM)简化而来的门控循环单元 (gated recurrent unit，GRU)神经网络，不仅解决了序列的长期依赖问题，且网络结构简单、计算速度快，在机械故障诊断中表现出较好的预测能力[18]。因此，为了进一步提升自相关过程监控的效率，本文应用GRU神经网络对自相关过程数据进行预测，提出基于GRU神经网络的自相关残差控制图，并形成自相关过程的在线监控方法。通过仿真实验与基于AR (1)模型残差控制图、基于BPN残差控制图、基于SVR残差控制图的平均运行链长 (average run length，ARL)进行对比分析，验证了所提方法对自相关过程均值阶跃监控的有效性。

1 循环神经网络

循环神经网络RNN是深度学习方法中的一种，其当前状态兼顾了整个时序数据的先前信息，适宜于对时序信号进行分析预测。RNN最显著的特点是隐层自连接，当前t时刻隐层的状态是由前t-1时刻隐层状态更新而来的，网络结构如图1所示。

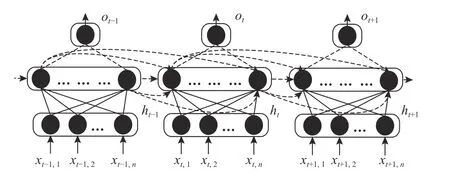
图1 循环神经网络的基本结构Figure 1 Basic structure of recurrent neural network

对于长度为T的时间序列，选取其交叉熵误差作为RNN的损失函数，具体可表示为

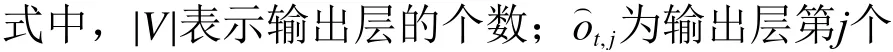
2 门控循环单元神经网络

长短时记忆网络LSTM是RNN的一种变体，该网络正是为了解决RNN出现梯度消失以及梯度爆炸问题而提出的[19]。LSTM 采用记忆体替换RNN隐层中的神经元，能够对时间序列的信息进行保留和长期记忆。单个时间步的LSTM网络结构如图2所示。

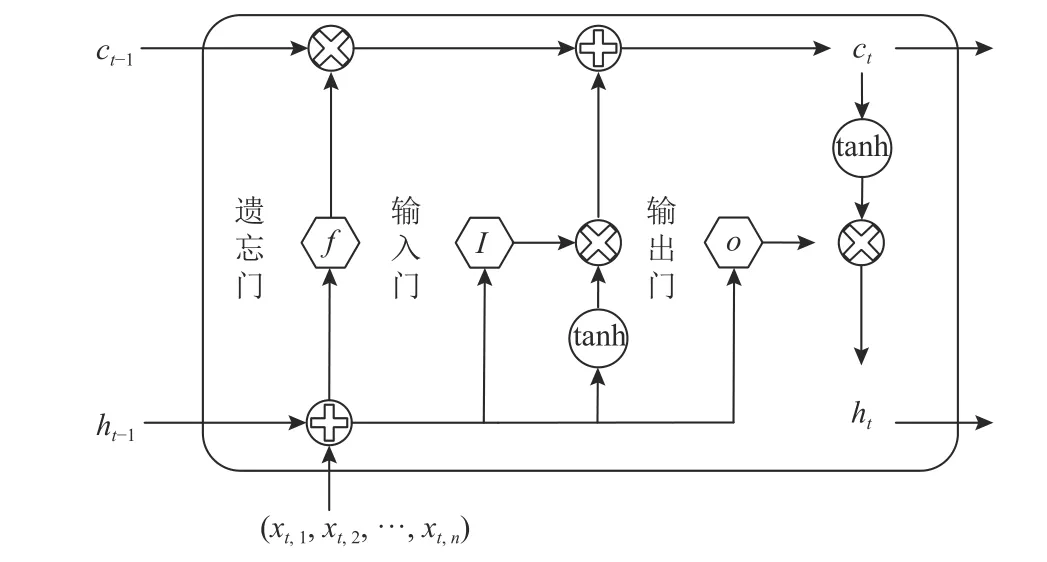
图2 单个时间步的LSTM网络结构Figure 2 Network structure of LSTM with single time step

LSTM通过遗忘门 (forget gate，FG)、输入门(input gate，IG)和输出门 (output gate，OG)实现对数据序列的保留和长期记忆。FG决定当前时刻网络的状态有多少信息需要保存到内部状态中，而输入门则决定过去的状态信息有多少需要丢弃。最后，由输出门决定当前时刻的内部状态有多少信息需要输出给外部状态。

3 自相关过程的在线监控

3.1 数据说明

在训练阶段，采用自相关过程受控状态下的正常时序数据对GRU网络进行离线训练。在测试阶段，采用自相关过程不同阶跃幅值的时序数据测试基于GRU网络的残差控制图的监控性能。应用蒙特卡罗仿真自相关过程受控状态下的正常时序数据，可表示为

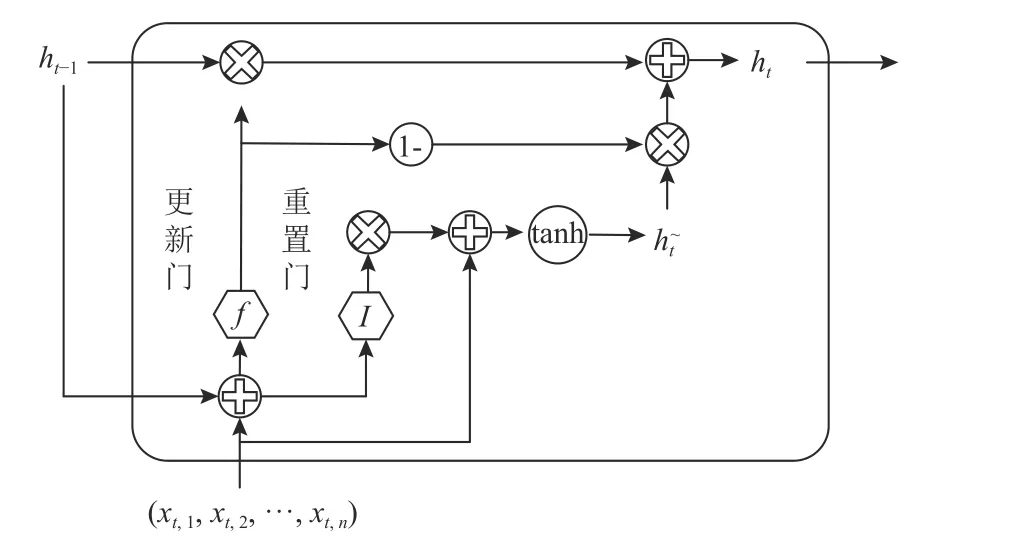
图3 单个时间步的GRU网络结构Figure 3 Network structure of GRU with single time step

3.2 基于GRU网络的残差控制图

采用处于受控状态的时序数据对GRU网络进行离线训练与测试，在不同时刻滑动窗口的向量作为GRU网络的输入，当前时刻的下一实测值为输出目标。对自相关过程时序数据进行预测的GRU网络循环计算过程如图4所示。

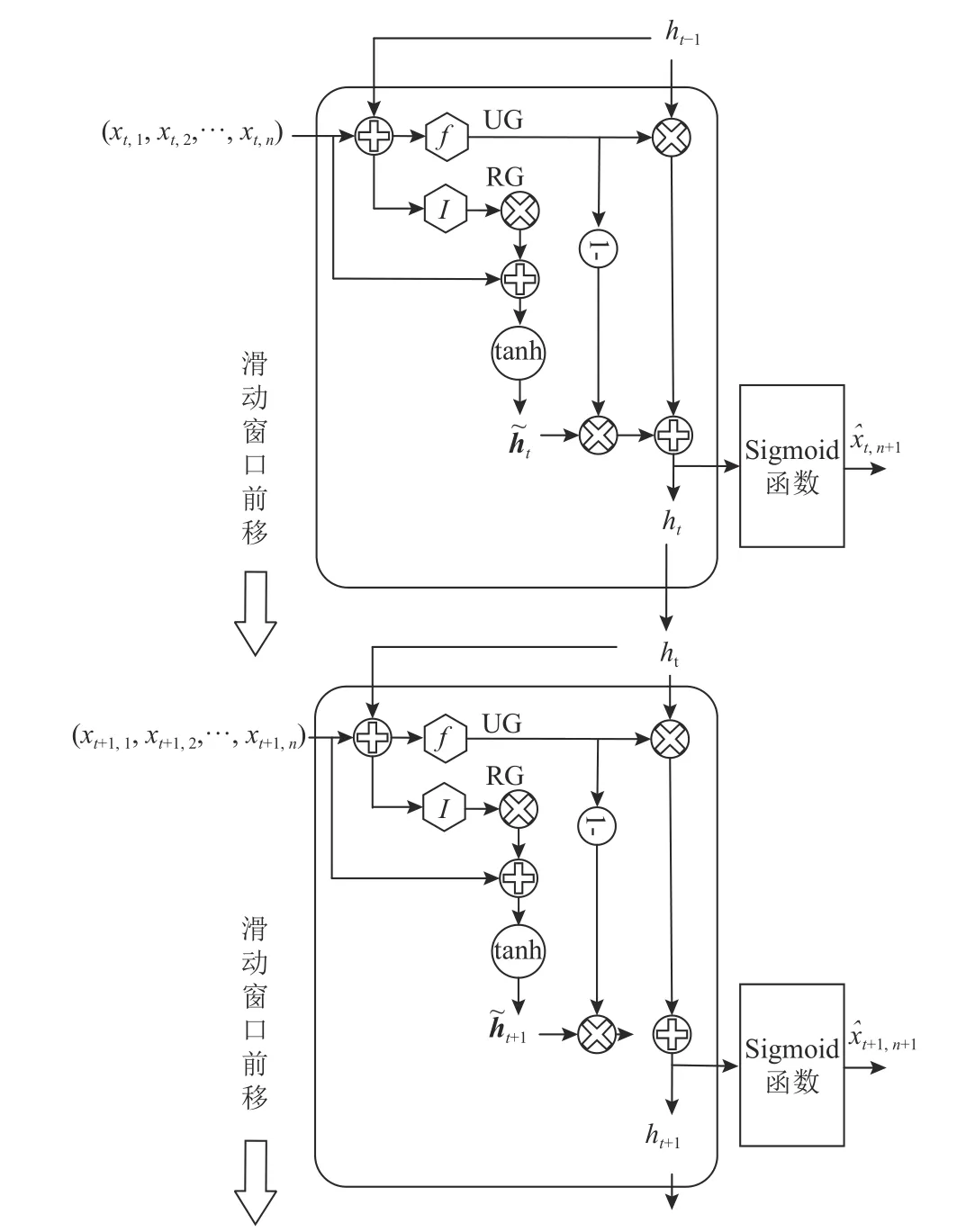
图4 时序预测GRU网络的循环计算过程Figure 4 Cycle calculation process of GRU network for time series prediction

采用滑动窗口方法获取GRU网络的训练和测试数据集。在训练阶段，学习得到窗口向量与输出向量间的映射关系，而后在测试阶段预测出当前时刻的下一个测量值。依据不同时刻的预测值，构建基于GRU网络的自相关残差控制图，具体的构建步骤如下。

步骤1 收集自相关过程处于统计受控状态下的时间序列数据；

步骤2 采用滑动窗口方法形成GRU网络的训练、测试样本数据集；

步骤3 初始化GRU网络的参数，利用训练样本数据集对其进行离线训练；

步骤4 当预测误差满足预定要求时，形成训练良好的GRU；

步骤5 计算预测值与实际值间的预测误差，选取该误差作为残差控制图中的监控变量；

步骤6 依据第1类错误为0.27%，即受控ARL为370的原则，确定残差控制图的控制限。

3.3 在线监控流程

应用基于GRU网络的残差控制图对自相关过程进行在线监控，包括分析用残差控制图的离线构建和控制用残差控制图的在线过程监控两个阶段。具体的应用流程如图5所示。离线阶段，训练GRU网络对受控状态下的时序数据进行非线性拟合，通过预测误差构建出分析用残差控制图。在线监控阶段，测试数据被输入到训练好的GRU网络以预测过程波动，然后采用控制用残差控制图判定当前过程是否失控。

图5 基于GRU网络的残差控制图在线监控Figure 5 Online monitoring of residual control chart based on GRU network

在图5中，虚线上方为分析用残差控制图的构建过程，其具体的实现步骤见3.2节中的步骤1 ～ 6。虚线下方为构建控制用残差控制图的构建过程，具体过程如下。

步骤1 采用滑动窗口取值形成自相关过程的测试样本数据集；

步骤2 针对测试样本数据集采用离线训练好的GRU网络对其进行预测；

步骤3 将分析用残差控制图的控制限赋值于控制用残差控制图，并将预测误差绘制到残差控制图中；

步骤4 若残差超过控制限或在控制限内排列非随机，则进行失控报警，否则执行步骤1。

4 仿真实验及分析

4.1 数据的产生

采用式 (8)蒙特卡洛仿真公式仿真自相关过程受控状态下的时序数列数据X(t)，并依据监控窗口大小为25，采用式 (9)将时序数列数据整理为GRU网络的训练样本数据。其中，自相关系数Φ分别取值为0.25、0.45和 0.75。针对每种自相关系数分别产生500组滑动窗口为25的训练样本数据。采用式(10)仿真自相关过程阶跃状态下的时序数据。其中，阶跃幅度δ取值为0.5、1.0、2.0和3.0。

4.2 性能分析

1) 受控过程的ARL分析。

根据监控独立观测值的休哈特控制图原理, 如果被监控变量是相互独立的, 受控过程的平均运行链长应当近似等于370。因此，为验证采用GRU网络构建残差控制图的有效性，分别采用一阶自回归模型AR (1)、BP神经网络以及支持向量回归3种不同方法进行预测，而后对预测误差采用休哈特控制图进行监控，连续运行100次，取所有在受控状态下链长的总平均得到ARL，见表1。

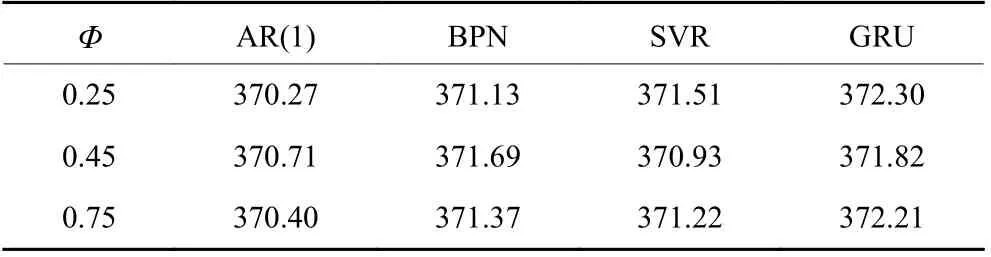
表1 受控过程的ARL对比Table 1 ARL comparison of in-controlled process

由表1可知，休哈特控制图监控上述3种方法产生预测误差的ARL都较接近于理论值370。其中，基于机器学习方法的受控状态下ARL比基于AR (1)模式的受控状态下ARL要大，说明采用机器学习方法进行预测，而后应用残差控制图进行监控对自相关过程发生误报的概率要小。有GRU网络预测的受控状态下ARL值可知，采用GRU网络构建残差控制图对自相关过程进行监控是有效的。

2) 失控过程的ARL分析。

为进一步验证基于GRU网络残差控制图的监控能力，对不同均值阶跃幅值的自相关过程对比基于不同机器学习方法和不同时间序列模型的残差控制图的失控ARL。其中，过程均值阶跃的幅度值以被监控误差的标准差为基本单位。基于不同机器学习方法残差控制图，基于不同时间序列模型残差控制图的失控ARL，分别见表2和表3。

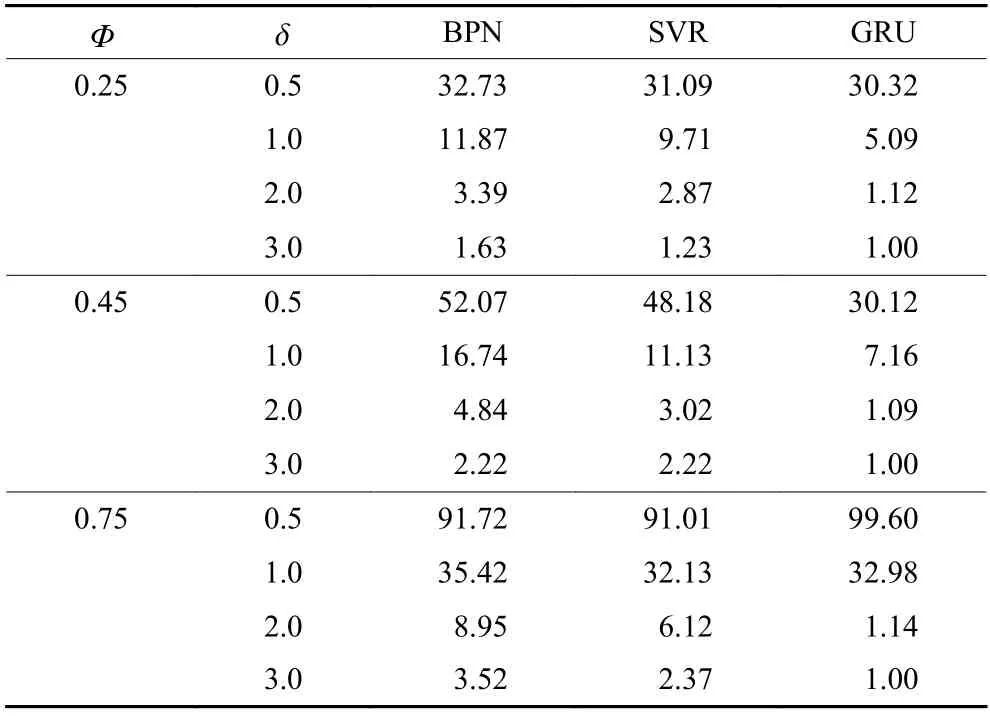
表2 不同机器学习方法的ARL对比Table 2 ARL comparison with different machine learning methods

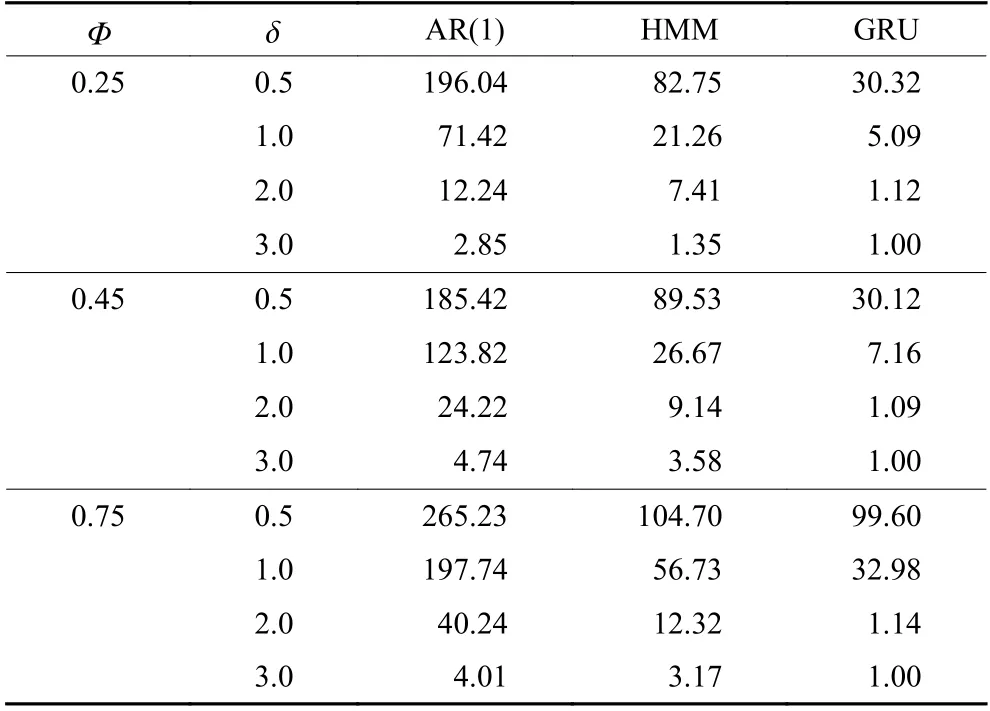
表3 不同预测方法的ARL对比Table 3 ARL comparison with different prediction methods

由表2和表3可知，在均值阶跃幅值超过1倍标准差的情况下，基于机器学习方法残差控制图的失控ARL值均小于基于时间序列模型残差控制图的失控ARL值。这说明基于机器学习方法的残差控制图对自相关过程监控时，对过程均值阶跃较为灵敏。其中，在均值阶跃幅值等于或大于2倍标准差的情况下，基于GRU网络残差控制图的失控ARL值都比较接近于1。这充分验证了所提残差控制图对自相关过程监控的有效性。

5 结论

为了进一步提升自相关过程监控的效率，应用GRU神经网络对受控状态下的自相关过程数据进行预测，提出基于GRU神经网络的自相关残差控制图，并详细说明应用所提残差控制图的在线监控方法。利用深度门控循环单元神经网络，该方法能够识别具有不同自相关系数的各种相关过程的均值漂移。通过与基于一阶自回归模型AR (1)、BP神经网络以及支持向量回归3种不同方法残差控制图的ARL性能对比，所提的基于GRU神经网络的残差控制图对自相关过程均值偏移具有良好的监控性能。本文的研究能有效应用于多变量自相关过程运行状态的监控中。另外，应用深度学习方法对自相关过程进行异常原因诊断仍需进一步深入研究。