基于联合典型变量矩阵的多阶段发酵过程质量相关故障监测

高学金，何紫鹤，高慧慧，齐咏生

（1 北京工业大学信息学部，北京 100124； 2 计算智能与智能系统北京市重点实验室，北京 100124；3 内蒙古工业大学电力学院，内蒙 古呼和浩特 010051）

引 言

间歇生产方式以其多品种、小批量、高附加值的优势成为保证产品高质量的重要手段[1-4]。在间歇过程中，操作条件的异常容易引起过程故障，如果影响到产品质量，则认为是发生质量相关的故障，可能造成重大经济损失。例如，发酵过程作为间歇过程的一种典型过程，由于生产进程是不可人为逆转的，并且发现故障往往有一定的延迟时间，一旦没有及时检测并排除故障，极易导致不必要的成本浪费。所以，建立一个合理、有效的监控体系，对生产过程进行实时、精确的故障监测，最大限度地抑制质量下降和重大经济损失，就显得至关重要[5-6]。合理的质量相关的故障监测方法能够保证间歇过程的安全性、产品质量的稳定性和生产的高效性，主流方法包括典型相关分析(CCA)[7-8]以及偏最小二乘(partial least squares,PLS)[9-12]等。

多阶段特性是发酵过程中的一个典型特性[13-14]，传统的单一模型应用于连续过程时能取得良好的效果，但是并不适用于间歇过程。因此，许多国内外专家针对阶段划分问题进行了探索。Yu 等[15]提出基于高斯混合模型(Gaussian mixture model, GMM)的方法，达到分阶段建模的目标。Lu 等[16]提出基于K-means 聚类的阶段划分方法，对时间片归类并建立监控模型。以上方法均将过渡阶段硬性归属到每个稳定阶段中，不能很好地反映过渡阶段的特性，相邻两个阶段切换期间的过渡，是一种渐变的动态趋势。针对阶段划分中的硬分类问题，Zhao等[17]提出一种阶段软划分方法，在K 均值方法的基础上利用负载矩阵区分阶段和阶段间过渡的变化，揭示了过程潜在特性的行为规律。Ng 等[18]提出基于重叠PCA 的分段监测方法，通过模糊C均值得到的隶属度信息划分稳定阶段与过渡阶段。上述方法解决了硬划分造成的监控性能低下的问题，但均建立在过程数据服从静态独立分布的假设下，忽略了实际过程变量的测量点前后相互关联的特性，因此对过程动态特征变化的捕捉不够灵敏。针对划分阶段中的动态性问题，李征等[19]提出基于信息增量的阶段划分方法，利用信息增量结合滑动窗技术捕获系统的动态特性。Zhao 等[20-21]提出一系列步进有序的阶段划分方法，以过程特征对故障监测性能的影响来捕捉过程的动态特征变化。但是以上方法仅对时序相关性进行解析，缺乏对过程数据变化的充分解析和判断，无法区分过程强动态变化与正常阶段切换，往往得到粗糙甚至错误的划分结果，导致监测结果跳变点控制限异常的情况。以上大多数阶段划分方法仅依据过程变量信息划分阶段，忽略了质量变量信息，对于阶段内变量信息描述不完全，进一步导致划分结果不理想，在质量相关故障监测的过程中可能给出错误的结论。在同一生产阶段内的不同时刻，过程变量与质量变量间的相关关系具有较高的相似性，不同时段间则是有差异的[22]。因此，质量变量是无法忽略的关键因素，也是客观反映间歇过程多阶段特性的重要指标。

针对以上问题，本文提出一种基于联合典型变量矩阵的两步阶段划分方法，并在子阶段建立CCA故障监测模型。该方法首先将沿批次展开的二维数据矩阵划分为不同的时间片，利用对每个时间片矩阵进行典型相关分析得到的原始典型变量矩阵构建联合典型变量矩阵，之后对联合典型变量矩阵进行K 均值聚类，实现基于静态特征的第1 步划分；然后采用慢特征分析(SFA)算法提取表征过程动态性的慢特征，并用K 均值算法对其进行第2 步划分，综合分析两步划分结果确定最终的稳定阶段和过渡阶段，最后建立分阶段CCA 监测模型。

1 基本理论

1.1 典型相关分析

典型相关分析由Hotelling[23]提出，CCA 是研究两组变量X与Y相关性的一种统计方法。给定一组从生产过程操作中收集到的数据，其中矩阵X是过程变量，矩阵Y是质量变量。

在建立CCA 模型时，为了研究X与Y这两组变量的相关性，需找到投影方向A和B，通过研究投影ATX与BTY的相关关系来确定两组原始变量间的相关关系。

CCA 方法的核心思想就是寻找最优的正交投影方向A和B，使得原始变量X和Y在此方向的投影的Person 系数最大化，其目标最大化准则函数为：

式中，E为与BTY弱相关的噪声信号，但是与ATX不相关。

CCA 将X和Y看成整体，通过构造新的典型变量矩阵U=ATX，V=BTY，分析两个变量组之间的联系。在同一生产阶段内的不同时刻，过程变量与质量变量间的相关关系具有较高的相似性。典型变量矩阵U和V在分别包含过程变量与质量变量信息的同时可以确保特征之间的关联最大化[24]，从而突出和增强过程变量与质量变量之间关系的变化对划分阶段的重要影响，因此典型变量矩阵的相似性可以表征生产过程的阶段变化，从而提高阶段划分精度。

1.2 慢特征分析

慢特征分析是一种提取动态信息的方法[25]。SFA通过特征映射可以将输入的时间序列转变为缓慢变化的输出信号，即输入信号所隐含的慢特征(slow feature, SF)。给定一个m维输入信号x(t)=[x1(t),x2(t),…,xm(t)]T，SFA 的目标是找到一个特征映射g(x)=[g1(x),g2(x),… ,gQ(x)]T，使得慢特征s(t)=[s1(t),s2(t),… ,sQ(t)]T，sq(t)=gq(x(t))变化最慢，SFA 的优化问题表达式如下：

发酵过程数据具有非线性特征，为了从非线性的过程数据中提取慢特征信息，众多学者分别提出了多种基于SFA的非线性算法。其中比较典型的是二项式的非线性扩展方法[25]和核SFA[26]。核SFA 虽然在一定程度上解决了非线性问题，但其主要缺点在于算法容易退化导致过拟合，且难以选择合适的核函数进行有效的非线性变换。因此，为丰富特征空间、兼顾算法可行性。本文采用二项式的非线性扩展方法。给定输入为x(t)={x1,x2,…,xm}，二次扩展函数为v͂(x)=[x1,x2,…,xm,x1x1,x1x2,…,xmxm]，然后中心化扩展后的数据v͂(x)使其均值为0 得到v(x)，其维度为m+m(m+1)/2，这样就将非线性情况转化成了扩展空间里的线性情况。

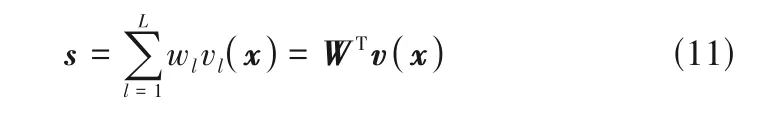
对式(9)求取广义特征值时，为了方便计算，利用奇异值分解进行白化操作以满足约束式(7)，SFA的二维几何解释如图1 所示。输入x(t)及其一阶导数ẋ(t)的协方差矩阵用实线椭圆和虚线椭圆标示于图1(a)中，白化矩阵z(t)及其一阶导数ż(t)的各向同性协方差用实线圆圈和虚线椭圆标示于图1(b)中，经过白化的慢特征s满足各向同性高斯分布，ṡ满足各向异性高斯分布。因此，慢特征体现了发酵过程的动态变化[27]。

图1 SFA的二维几何解释示意图Fig.1 The geometrical interpretation of SFA in two dimensions

发酵过程是一个缓慢时变的生化反应，其运行轨迹在同一间歇操作周期内部呈现出局部动态性，由于间歇过程受相同操作重复执行的影响，初始培养基容量逐渐增长使得批次运行轨迹在批次间逐渐变化，观测数据产生慢时变特性，导致各个批次间亦呈现明显的动态变化。图2 为运行轨迹的示意图。

图2 慢时变发酵过程轨迹示意图Fig.2 Illustration of slow-varying fermentation process trajectory

SFA 可以将快速变化的成分摒弃，提取出时序样本中变化最缓慢的本质特征，这些特征包含着批次间缓慢波动的动态演化信息，这种动态信息不仅能够表征导致过程动态时变的潜在驱动力，而且能够真实地反映过程变量随时间变化的总体趋势，因此SFA 能更加充分地提取发酵过程的动态特征。

2 基于联合典型变量矩阵的多阶段发酵过程质量监测

2.1 基于联合典型变量矩阵的两步阶段划分

发酵过程的训练集包括历史过程数据和历史质量数据，分别以三维矩阵X(I×Jx×K)和Y(I×Jy×K)表示。其中，I为批次数；Jx、Jy分别为过程、质量变量个数，质量变量包括菌体浓度和产物浓度等；K为每个批次的采样时刻数。本文假设建模所需的各批次操作时间都是等长的。

为考虑质量变量对生产过程阶段划分的影响，本文结合过程变量的典型变量矩阵U和质量变量的典型变量矩阵V，构建联合典型变量矩阵。将每个时间片的联合典型变量矩阵使用K-means 聚类算法进行初步划分，由于每个联合典型变量矩阵是对每个独立时间片采用CCA 算法得到的，同时传统的CCA 算法是静态的，所以得到的结果忽略了每个时间片的动态特征，因此认为使用K-means 聚类算法是对原始数据的静态特征进行的聚类，得到的聚类结果只能反映出原始数据大致的分布特征。发酵过程的动态性往往与生产阶段密切相关，因此有必要将能表征过程动态性的动态特征提取出来进行再次划分。

使用SFA 进行动态特征提取，最小化时间片矩阵在每个采样时刻上不同批次间的变化，然后将所有批次得到的慢特征进行组合得到慢特征时间片，使用K-means 聚类算法对所有时间片进行再次划分。为了精确地区分过程强动态变化时刻与阶段切换时刻，利用DPRF(differential phase recognition factor)指标观测动态波动情况，有效综合利用静动态划分结果，对阶段切换点精准定位，依据切换点对应的采样时刻k，实现间歇过程的阶段划分。图3 为基于联合典型变量矩阵的两步阶段划分方法的流程图，具体步骤如下。

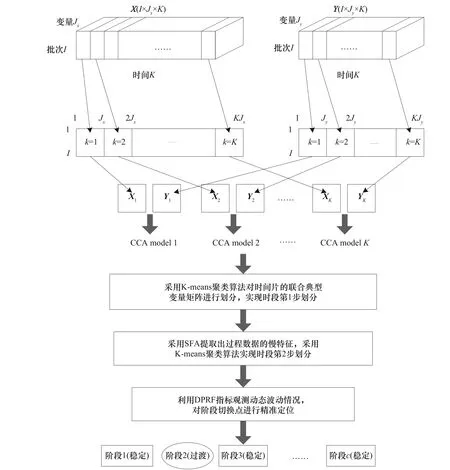
图3 基于联合典型变量矩阵的两步阶段划分Fig.3 Two-step phase partition based on joint canonical variable matrix

(1) 将三维过程测量数据X(I×Jx×K)沿批次方向展开为K个二维时间片矩阵Xk(I×Jx)，k=1,2,…,K。同理，将质量测量数据Y(I×Jy×K)进行相同的处理得到Yk(I×Jy)。

(2)将沿批次展开后得到的二维时间片矩阵Xk(I×Jx)进一步进行中心化和归一化：

式中，j=1,2,…,Jx；k=1,2,…,K；xˉk,j为第k采样时刻第j个过程变量的均值；xk,j为第k采样时刻第j个过程变量；Sk,j为第k采样时刻第j个过程变量的标准差。

(3)对每个标准化时间片数据进行典型相关分析，得到相应的Xk的典型变量矩阵Uk和Yk的典型变量矩阵Vk，Uk和Vk分别完整表达了Xk、Yk的每个特征之间的联系，以及分别对Xk、Yk整体相关关系的影响，形式如式(13)和式(14)所示：

式中，Ak为第k时刻过程数据Xk(I×Jx)的投影矩阵；Bk为第k时刻质量数据Yk(I×Jy)的投影矩阵。

为了最大程度地融合原始数据的基本信息，同时确保特征之间关联最大化。针对每个采样时刻k(k=1,2,…,K)，将质量变量的典型变量矩阵Vk扩展到过程变量的典型变量矩阵Uk中，由于Uk和Vk有最大的Person 相关系数，因此构建相应联合典型变量矩阵Tk，得到式(15)：

(4) 对联合典型变量矩阵使用K-means 聚类算法进行划分，实现生产过程的初步划分。K-means算法原理如下。

K-means 算法的输入是数据点之间的相似度，考虑到第1 步划分是基于数据的静态特征，因此测量数据常常包含噪声或奇异值，可能会导致把当前阶段的数据错分到其他阶段中的现象，在线监测时产生漏报和误报，为此将采样时间k扩展到联合典型变量矩阵Tk(k=1, 2, … ,K)中得到扩展联合典型变量矩阵T̂k=[Tkk]。本文利用数据集的相似度指标[28]定义每个扩展联合典型变量矩阵T̂k与其他时刻扩展联合典型变量矩阵T̂i(i=1,2,…,K，且k≠i)的相似度：

(5) 计算标准化时间片矩阵X͂k的慢特征，首先进行非线性扩展，即对标准化数据中的输入样本进行二阶非线性扩展并中心化扩展后的数据得到v，用v替换式(8)中的x，即实现了非线性情况向线性情况的转化，之后的步骤与线性求解相同，需要分别计算矩阵M和N，并根据式(9)做广义特征值分解，求得向量矩阵W。采用式(11)求出所有的慢特征s={si,i=1,2,…,Jx+Jx(Jx+1)/2}，将不同时刻每个批次的慢特征组合成为慢特征时间片Sk(k=1,2,…,K)。通过剔除比所有输入变量变化都快的慢特征信息[29]，从而确定所要提取的慢特征数目D，计算方法如下：

(6)间歇过程与另一种重要生产过程——连续过程相比，具有其特殊性，主要区别在于始终处于操作条件改变频繁和非稳定工作状态下，即同一个生产批次中不存在稳态工作点，产品和操作改变频繁。如图4 所示，讨论了动态波动的两种正常情况。一种是不同阶段之间的正常切换，另一种是由于原料变化、外部操作环境等因素引起的某一阶段呈现强动态变化。这种动态波动是一种不同于阶段切换的随机行为。因此，为了提供更精确的划分结果，需要对这两种情况进行区分。阶段识别因子(phase recognition factor, PRF)[30]指标度量不同批次运行轨迹在相同采样时刻上的变化快慢。

图4 间歇过程动态波动的两种正常情况Fig.4 Two normal cases for the dynamic deviations of batch process

利用慢特征分析得到的慢特征矩阵Sk,D计算不同批次在第k个采样时刻上的缓慢变化程度：

PRF 值越大，不同的批次轨迹在相同采样时刻上变化越快。相较于发酵过程的稳定阶段平稳的运行模式，过渡阶段呈现出更强的过程波动和更高的不确定性，因此不同的批次在稳态阶段的相似性更显著，也就是稳态阶段的PRF 值通常远小于过渡阶段的PRF 值。为了观测动态波动情况，定义两个相邻时间切片之间的DPRF(differential PRF)指标：

式中，k=2,3,…,K。基于DPRF 指标，能够观测动态波动情况。当DPRF 出现明显变化时，其对应的采样时刻既可能是同一个阶段内的强动态变化点，也可能是处于不同阶段切换期间的阶段切换点。

(7)为了精准区分过程强动态变化点与阶段切换点，结合两步划分结果实现对跳变点的判断：①两步划分结果重叠区域中间不会存在阶段切换点，可能会出现强动态变化点；②阶段切换点均分布于两步划分结果非重叠区域。因此，忽略隶属于两次划分结果的重叠区域的DPRF 跳变点，将隶属于两次划分结果非重叠区域的DPRF 跳变点确定为阶段切换点。依据切换点对应的采样时刻k，将生产过程分为稳定阶段和过渡阶段。

2.2 离线建模

在完成基于联合典型变量矩阵的阶段划分结束后，需要分别对每个阶段数据建立监测模型，计算出相应统计量的控制限，用于后续的过程在线监测。

(1)首先以批次展开的方式将每个阶段的历史过程数据Xc(I×Jx×K)转换成Xc(I×KcJx)，其中Kc是阶段c对应的采样时刻；其次对Xc(I×KcJx)按式(12)做标准化处理，再沿变量方向展开得到Xc(Jx×KcI)。对质量数据Yc(I×Jy×K)做相同处理得到质量数据矩阵Yc(Jy×KcI)。

(2)对以变量展开后每个阶段的二维过程数据和质量数据，建立CCA监测模型，模型表达式如下：

式中，Ac、Bc为投影方向；Λκ,c为对角阵；Ec为残差矩阵。

(3)分别计算正常操作条件下的质量无关故障的监测统计量Tx2统计量、质量相关故障的监测统计量Ty

2统计量及样本控制限。

2.3 在线监测

(1)在新批次的采样时刻k，采集过程变量数据xnew,k(1×Jx)和质量变量数据ynew,k(1×Jy)，采用离线建模的均值和方差对其标准化。

(2)根据采样时刻k对应的阶段，选择相应的监控模型，计算此时刻的统计量控制限：

若Tx2未超出控制限，Ty2超出控制限，则说明生产过程发生质量有关的故障，过程数据未发生故障，质量受到除了过程数据以外的因素影响造成故障；

若Tx2、Ty2均超出控制限，则说明生产过程发生质量相关的故障，过程数据发生故障且会导致质量故障。

3 实验结果与分析

3.1 仿真实验

青霉素发酵过程是典型的间歇过程，整个发酵过程，一般最为关注的质量变量为青霉素浓度，过程监测的焦点集中于影响最终产品质量的故障。本文基于青霉素仿真平台Pensim[31-32]进行实验仿真，表1为初始值和参数值的取值范围，具体设定步骤为：设定每批次发酵时间为400 h，采样时间间隔为1 h，按照表1 对初始条件和参数值随机取值，10 个过程变量和2 个质量变量用于监测，如表2 所示。为了模拟青霉素实际发酵过程，对变量均进行白噪声处理。本文选取40批正常数据组成样本集，其中包括过程测量数据X(40×10×400)和质量数据Y(40×2×400)，另外2 个故障批次用于测试，故障设置如表3所示。

表1 初始条件及控制参数设置Table 1 Initial condition and control parameter settings

表2 建模所用变量Table 2 Variables used for modeling

表3 故障设置信息Table 3 Fault settings

图5 为采用本文方法得到的划分结果，本文用CCA 处理数据时，根据95%的累计方差贡献率[33]选取主元数目为2。按式(16)计算相似度指标Sk(k=1,2,…,400)，作为K-means 算法的输入样本。观察划分结果可明显看出整个生产过程被明显地初步划分为4 个阶段：1～86 h，87～200 h，201～286 h，287～400 h。

图5 青霉素发酵过程阶段划分结果Fig.5 Phase partition result in penicillin fermentation process

采用SFA 提取慢特征，通过式(18)确定最佳的慢特征个数，最终选取前5 个慢特征。然后按式(19)计算相似度指标S′k(k=1,2,…,400)，输入Kmeans 算法进行再次划分。观察结果可知，过程被再次划分为4 个阶段：1～23 h，24～174 h，175～238 h，239～400 h。上述两步划分结果不一定严格与菌体生长阶段一致，但能够获得分阶段建立故障监测模型时注重的数据特征。为了区分强动态变化点与阶段切换点，利用DPRF 指标观测动态波动情况。为清晰地呈现DPRF 指标于两步阶段划分的当前结果图中，此处将所有DPRF 值垂直向上平移了2 个单位。DPRF 绝对值越大表示波动水平越高，最大值对应的采样时刻是最可能的切换点。为了合理判定波动水平高低，通过多次实验将采样点DPRF 指标绝对值的平均值作为临界值，在该仿真实验中将临界值确定为1。如果DPRF 的绝对值比1 大则认为波动水平很高，并且隶属于两次划分结果的非重叠区域，则可以定位阶段切换点，图5 中使用虚线椭圆标出了6 个阶段间的切换点，分别是32、58、180、191、262、275 h 时刻，最后综合分析划分1～31 h，59～179 h，192～261 h，276～400 h时刻为稳定阶段，32～58 h，180～191 h，262～275 h时刻为过渡阶段。

本文将提出的算法与其他阶段划分方法进行比较，包括步进有序时段划分(step-wise sequential phase partition, SSPP)方法[20]和基于信息增量矩阵-偏最小二乘(information increment matrix-partial least square, IIMPLS)方法[19]。对于SSPP 算法，当容忍因子值α=4 时，整个过程被分为三个阶段，即1～38 h，39～179 h，180～400 h。但是划分结果并没有反映出过渡阶段的特性，并不符合实际的物理过程。图6 为限制因子θ=3.3 和3.0 时，IIMPLS 的阶段划分结果。限制因子θ取值为3.0 时，46、67、149 和231 h 被确定为切换点。然而IIMPLS和SSPP 的阶段数目均随可调参数变化，需要根据先验知识选择合适的参数取值才能保证合理的划分结果。相比之下，本文提出的算法可以获得更准确、更可靠的结果，并且克服了可调参数的影响。

图6 IIMPLS方法对青霉素发酵过程的阶段划分结果Fig.6 Phase partition result using the IIMPLS method in penicillin fermentation process

为了更好地表明本文方法的可行性和有效性，将监控效果与不分阶段的CCA 方法(CCA)、不考虑质量变量只用过程变量的时间片矩阵求相似度进行两步阶段划分的CCA、用SSPP 进行阶段划分的CCA 方法(SSPP-CCA)和用IIMPLS 进行阶段划分的CCA 方法(IIMPLS-CCA)进行了对比验证，其中，SSPP 算法的容忍因子α取值为4，IIMPLS 算法的限制因子θ取值为3.0。用故障检测率和故障误报率定量衡量本文方法的有效性。

首先，考虑的阶跃故障1 是人为将搅拌速率变量降低10%，故障发生时间为200～400 h。这种故障是模拟青霉素进入发酵后期可能发生的搅拌电机故障，搅拌速率的降低致使供氧情况改变，但是此阶段需氧量减少，溶氧率超过了需氧率，这种故障引起溶氧下降的幅度对菌体浓度和产物浓度的影响甚小，因此这种故障是质量不相关的。

其次，考虑的斜坡故障2 是人为将底物流加速率变量降低15%，故障发生时间为200～400 h。这种故障是模拟青霉素发酵后期可能发生的进料泵泄漏故障，底物流加速率减小，直接导致青霉素培养基含量急剧下降，青霉素的产量明显地受这种故障引起的基质浓度下降幅度的影响，因此该故障为质量相关的故障。

从图7 展示的故障批次2 的监测结果中可以发现，总地来说五种方法的Tx2统计量有相近的有效检测率，但是在故障发生阶段Ty2统计量较容易产生漏报，主要原因是与阶跃式故障相比，斜坡式的故障发生比较缓慢，不是突变故障。图7(a)、(c)和(d)质量相关故障检测率低下。相比较图7(e)来看，图7(b)Ty2统计量对200 h 加入的15%斜坡故障在286 h 才监测到，存在很大的延迟，原因在于图7(b)在阶段划分时未考虑质量变量信息，因此在质量相关的故障监测时存在较多漏报。从图7(e)的监测结果可以发现，Ty2统计量故障检测率明显高于其他四种方法，本文所提方法更及时地显示质量相关故障的发生，减小了因传统对整个批次建模而引起的偏差，从而保证了对质量相关故障的及时检出。表5 为五种方法在故障批次2 下误报与检测率的对比结果。

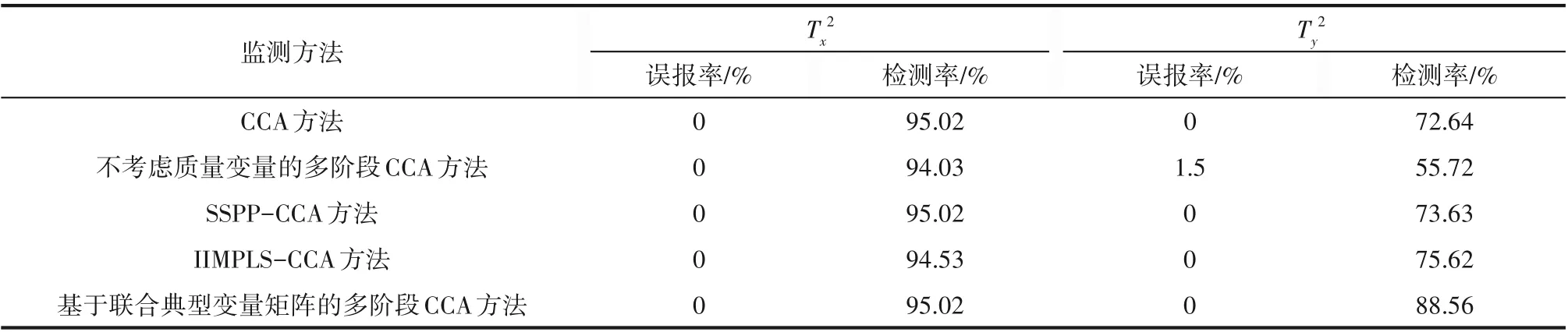
表5 故障批次2的误报率和检测率对比结果Table 5 False alarm rate and fault detection rate of false batch 2

3.2 算法实际验证

白介素-2 是治疗肿瘤癌症等疾病的药物，是通过大肠杆菌发酵获得的，其生产过程属于多阶段间歇过程。为了更多更好地获取具有医药价值的白介素-2，对大肠杆菌发酵过程采取精细化质量控制非常重要。本文选取北京某生物制药厂的大肠杆菌发酵过程实际生产数据进行算法验证，现场发酵过程的持续时间为6.5 h，每隔10 min 进行一次采样。与仿真实验相比，现场实验更易遭受外界环境的干扰，使得变量面临的不确定性因素增加，表现出更为强烈的动态特性，因此实际生产数据验证更突显所提方法的实际意义和效果。实验中，选取8 个过程变量(酸碱度、溶解氧、浓度罐压、温度、搅拌速率、补碳、补氮、通风速率)和1 个质量变量(菌体浓度)。在实际发酵过程中，各批次实际操作的不同导致批次间数据长度不相等。对于这种情况，有两种简单的处理方法。第一种为最短长度法，即找到最短的一批数据，将其余批次的数据进行截取使得它们也具有这个最短的长度[34]；第二种方法为利用最长批次的数据进行建模，将较短批次所缺的那部分数据当作“缺损数据”来处理[35]。本实验采用最短长度法，即找到最短的一批数据，将其余批次的数据进行截取使得它们也具有这个最短的长度，将数据处理成周期为390 min，即每个批次具有39 个采样点。采集20 批实际生产正常数据组成历史训练集，即过程测量数据X(20×8×39)和质量数据Y(20×1×39)。在实际的工业发酵现场，大肠杆菌发酵过程有3 个阶段：种子培养阶段、快速生长阶段和产物合成阶段，其中第13 和21 个采样点为阶段转换时刻，对应菌体生长和产物合成的时刻[36]。另外由于测量条件的限制，只有在第10～39 个采样点之间人为引入通风速率的阶跃故障批次数据，减少幅度为5%。

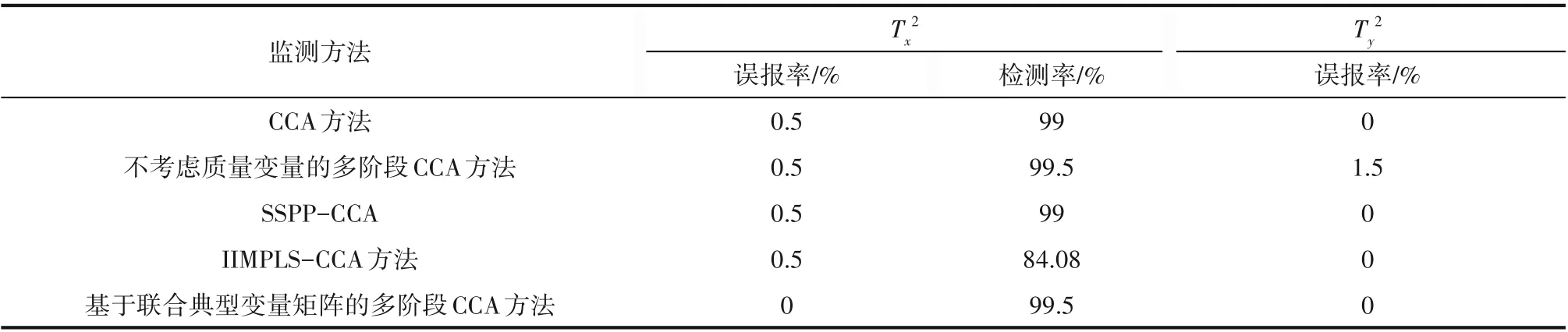
表4 故障批次1的误报率和检测率Table 4 False alarm rate and fault detection rate of false batch 1

本文所提方法的阶段划分结果如图8 所示，首先对大肠杆菌数据的联合典型变量矩阵采用式(16)计算相似度指标Sk(k=1,2,…,39)，之后利用Kmeans 算法进行第一步划分。第二步划分采用同青霉素发酵过程第二步划分相同的方法即可。然后利用DPRF 指标观测动态波动情况。为清晰地呈现DPRF 指标于两步阶段划分的当前结果图中，此处将所有DPRF 值垂直向上平移了0.03 个单位。为了合理判定波动水平高低，通过多次实验，将采样点DPRF 指标绝对值的平均值作为临界值，在该实际验证中将临界值确定为0.0351。忽略隶属于两次划分结果的重叠区域的DPRF 值跳变点，图8中使用虚线椭圆标出了4 个阶段间的切换点，分别是第12、14、21、23 个采样点，结合两步划分的结果，得到最终的划分结果为1～11，15～20，24～39 采样点为稳定阶段，12～14,21～23 采样点为过渡阶段。

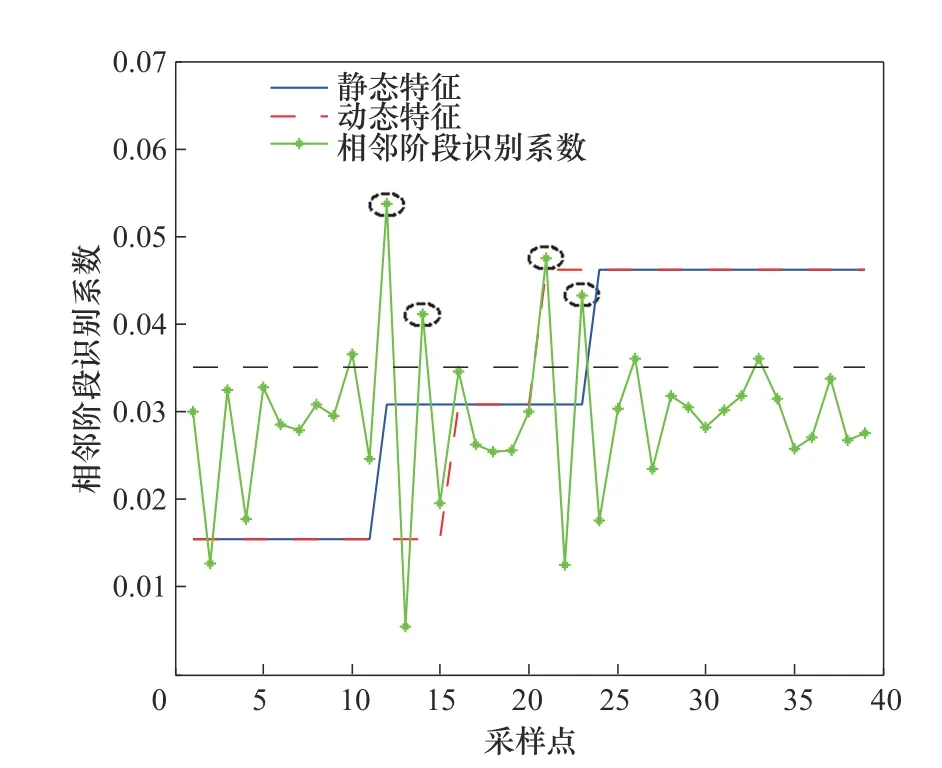
图8 大肠杆菌发酵过程阶段划分结果Fig.8 Phase partition result of E.coli fermentation process

表6 列出了采用IIMPLS(θ=2.1)和本文所提算法得到的划分结果的比较，其中实际切换点之前的划分点表示为误差。从表6 可以看出，IIMPLS 算法划分的第三阶段即产物合成阶段存在显著延迟，相比之下，本文所提算法给出的划分结果更合理，并且显著减少延迟。

表6 大肠杆菌发酵过程阶段划分的对比结果Table 6 Comparison of partition results of E.coli fermentation process

为使实验结果更具说服力，将监控效果与不分阶段的CCA 方法(CCA)、不考虑质量变量只用过程变量的时间片矩阵求相似度进行两步阶段划分的CCA方法进行了对比验证。

故障批次是在发酵中期即产物开始大量产生的阶段人为引入通风速率故障，通风速率变量从第10～39 采样点发生阶跃式降低，降低幅度为5%。通风速率的降低致使供氧情况改变，产物合成阶段需氧量增加，引起溶氧率下降，该故障会导致发酵罐内需氧小于溶氧，导致溶氧率的急剧降低，成为合成大肠杆菌的限制因素，最终影响产物的数量与质量。因此该故障为质量相关的故障。

图9 是三种方法对故障批次监测结果。图9(a)在故障起始阶段的漏报较多，图9(b)故障发生阶段存在较多漏报，对比之下，图9(c)中Tx

图9 大肠杆菌发酵过程故障批次的在线监测结果Fig.9 The online monitoring result of false batch of E.coli fermentation process

2统计量的故障检测率显著提高。说明本文所提阶段划分方法和监测模型的有效性。表7为三种方法在故障批次下误报率的对比结果。

表7 故障批次的误报率和检测率对比结果Table 7 False alarm rate and false detection rate of false batch

根据仿真数据和实际数据的阶段划分结果与在线监控效果，一方面证实了本文所提方法可以将整个发酵生产过程准确地划分为不同的稳定和过渡阶段，另一方面证明了本文所提方法可以显著提高质量相关的故障检测率，针对多阶段发酵过程的质量相关故障监测提供了合理和有效的解决思路。

4 结 论

大多数阶段划分方法仅依据过程变量信息将整个生产过程划分为多个子阶段，忽略了质量变量信息，且很少考虑过程的动态性。本文提出一种基于联合典型变量矩阵的阶段划分方法实现发酵过程质量相关故障监测，与前人工作相比，本文方法主要有以下优点：(1)构建的联合典型变量矩阵能合理融合原始过程变量和质量变量的特征信息，同时确保二者关联最大化，解决了由于忽略质量变量造成的划分结果不理想的问题，提高了质量相关故障检测率;(2)在利用传统CCA 提取静态特征的基础上，采用SFA 提取表征过程动态性的慢特征，通过动静协同的思想，分析原始数据的静态特征和动态特征实现两步划分，克服了因为不考虑数据动态性而导致的划分灵敏度下降的缺陷;(3)为了精确地区分过程强动态变化与正常阶段切换，引入相邻阶段识别系数(DPRF)指标观测动态波动情况，有效综合利用静动态划分结果，精准定位阶段切换点，从而将整个操作阶段划分为稳定阶段和过渡阶段，使得划分结果符合实际生产过程。青霉素仿真平台与大肠杆菌实际生产数据证明该方法具有可行性和有效性，为发酵过程的质量相关故障监测提供了一种可行方案。

符 号 说 明

F——F分布

g(·)——慢特征分析的特征映射

H——保留的慢特征集合

s——慢特征

ṡ——慢特征的一阶导数

x——输入信号

ẋ——输入信号的一阶导数

λ——特征值

ρ——Person系数

v(x)——零均值的二次扩展函数

v͂(x)——二次扩展函数

·t——时间平均

下角标

c——阶段

m——输入信号的维数

new——当前运行批次

Q——慢特征分析特征映射的维数

α——显著性水平

κ——主元个数