一种Web三维地形表面积测量方法

廖洋洋, 陈建华, 张 倩, 刘 帅, 粟 解

(1.成都理工大学 地球物理学院，成都 610059；2.阿坝州自然资源与科技信息研究所，汶川 623000)

0 引言

传统的地形测量由于其自身的局限且存在高危险性的隐患，在一些人不能到达的区域无法进行测量。随着地理信息技术与互联网技术的快速发展，三维实景地形模型已经能够在浏览器中呈现。在浏览器中最受欢迎的三维地理信息库是Cesium，它通过JavaScript封装的三维地理信息可视化的库，内部有大量的接口方便使用。三维WebGIS受到了越来越多的关注，其中对地形测量是其中的一个热点。Michael等[1]使用新的Web技术(如HTML5、WebGL)，实现高效的客户端分析，旨在推动基于Web的3D地理空间分析发展；Leila等[2]考虑到计算地形可见性问题，概述了在规则网格和不规则网格解决地形表面的算法；王恒[3]基于Cesium对地方大地测量平台数据库进行设计，提供了三维大地测量数据的展示、定位和查询；范俊甫[4]对Cesium框架多源电子地图瓦片方案进行设计，为地理信息系统与遥感技术项目应用提供了一种高灵活、低成本的解决方案；朱栩逸等[5]在GIS框架和Web服务的基础上，提出了一种基于Cesium的三维WebGIS搭建方案，并简单地实现了绘制功能；李伟等[6]使用ArcGIS软件的三维分析功能，通过建立数字高程模型，使用不规则三角网(TIN)，对鄱阳湖洪水淹没面积进行测量。

上述研究取得了较好的效果，但是目前的方法还无法满足Web环境下三维地形面积测量的现实需求。这里以三维开源地理信息库(Cesium)和地形切片技术为基础，重点针对真实三维地形模型的表面积测量进行研究，为地形测量提供一种有效、可靠的测量手段。

1 系统架构

系统架构图见图1。采用浏览器到服务器再到数据层的方式获取基本数据。根据Cesium官方文档说明，加载的地形格式数据可以为.terrain格式，使用CesiumLab开源工具，可以将数字高程数据格式转换为Cesium能识别的.terrain数据格式。使用IIS发布地形数据，Cesium内置有读取加载.terrain的方法，使用CesiumTerrainProvider方法可以加载已经发布的地形数据。将遥感影像数据使用Geoserver数据进行发布，使用Cesium内置imageryProvider方法加载发布好的影像数据，以便在有起伏的影像数据上绘制需要测量的区域。Cesium内置有许多方便的接口供我们使用，其中提供的接口方法sampleTerrainMostDetailed，可以快速地获取任何分辨率下地形切片任意一点最大精细程度的高度，而不必重新写一种前后端交互的新方法，也不需要后端操作DEM方法，这一种专门读取.terrain的方法，考虑到实现的复杂程度，所以采用前端计算的方式来实现整个算法，该方法主要针对Cesium提供一种计算思路。

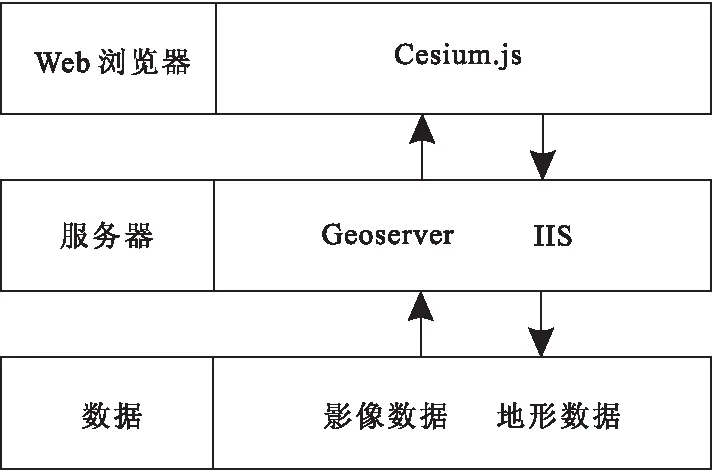
图1 系统架构

2 具体算法

2.1 算法流程

算法的整体流程如图2所示，通过绘制需要测量的区域，可以得到一个任意形状多边形，将多边形分解成为多个三角形，使用双线性插值的方法分别在每个三角形的最小边界矩形中插值，每个三角形各自判断插值过后的哪些点在自己内部，排除掉不在自己内部点，然后获取各自内部点的高度，将这些在内部的点重新连接起来构成新的三角网，从而计算每个小三角形的面积，以此类推，直到分割过后所有的三角形都计算完面积，最后累加求和，得到整个区域的面积。

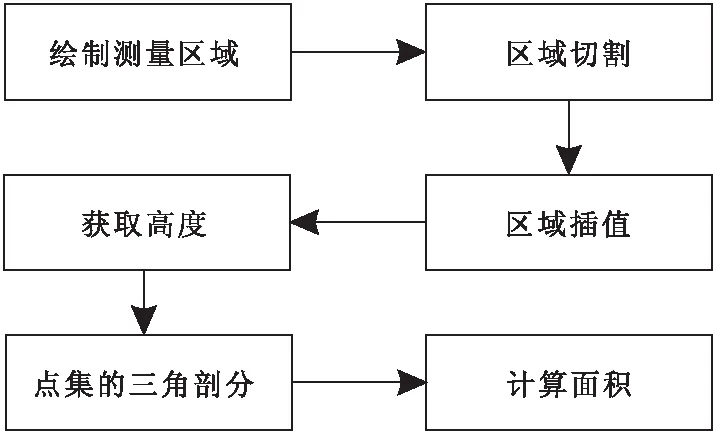
图2 算法流程

2.2 区域切割

利用Cesium的ScreenSpaceEventHandler方法，用来捕捉我们绘制区域的事件。考虑到绘制的区域可能是任意形状的多边形，这里使用耳切法(Ear Clipping)对区域进行切割。

耳切法：连续顶点V1、V2、V3组成的内部不包含其他任意顶点的三角形，将其称为简单多边形的耳朵(内角小于180°)[7]。V1与V3之间连接的线段称之为多边形对角线，点V2称为耳朵顶点。虽然可以认为三角形任何一个顶点都能是耳朵，但是原理上认为一个三角形只有一个耳朵。一个由4个以上顶点组成的多边形至少有2个不重叠的耳朵。根据这个理论特性，可以利用递归思想来解决三角形切割的方法。针对包含由n个顶点组成的简单多边形，找到其第一个耳朵，移除该耳朵顶点，此时剩余顶点将组成一个n-1个点的多边形。重复这个操作，直到剩余三个顶点，递归结束。

2.3 区域插值

若绘制区域不是三角形则区域切割后会形成至少两个以上的三角形，对每个三角形求取最小边界矩形。最小边界矩形是以三角形三个顶点(xk，yk)为基准，寻找出xmin、ymin、xmax、ymax4个值，然后以(xmin，ymin)、(xmin，ymax)、(xmax,ymax)、(xmax,ymin)4个点构成最小边界矩形。

当获取到每个三角形最小边界矩形的时候，使用线性插值方法，对每个最小边界矩形进行等间距插值。线性方程即线性插值的核心，使用线性插值的原因是因为其操作简单，并且能均匀地对地区进行插值覆盖。其已知两个点的坐标(x0，y0)与(x1，y1)，假设存在未知函数f，则函数上的一点可以表示为式(1)。

f(x,y)=f(x0)=w(f(x1)-f(x0))

(1)

其中w的比率为式(2)。

(2)

按照自定义精度在矩形范围内进行线性插值，精度越高，计算时间越长，然后将每个点与三角形进行判断，判断点是否在三角形内部。

获取到所有在三角形内部的点后，使用Cesium提供Sample Terrain Most Detailed方法就能获取每个内部的点的最大细化程度的高程值，。然后使用哈希表来存储每个点高程信息。

2.4 点集的三角剖分

将任意多边形区域切割成互相独立的三角形，然后再对每个三角形的内部进行插值，由此每一个三角形对应了插值后一个点的集合。每一个集合要做一个三角格网化，笔者使用Delaunay三角剖分算法对点集合进行三角格网创建。

实现Delaunay三角格网有Lawson算法和Bowyer-Watson算法等。Lawson算法是由Lawson在1977年提出，该算法具有思路简单明了、编程简单并且容易实现的优点，同时被称为逐点插入法[8]。Lawson的基本原理为首先创建一个包含散点集合中所有散点的简单多边形，将散点集合中未插入的散点逐一插入到三角格网中，并对新插入的点做空外接圆检测和局部调整，要求重新生成的三角格网均符合Delaunay准则，最后移除包含初始化的多边形顶点的三角形。

笔者使用改进的Lawson算法Bowyer-Watson算法实现地形三角格网剖分。Bowyer-Watson算法描述如下：

1)创建一个包含所有散点多边形或者三角形，放入链表中。

2)按顺序将集合中的散点插入到第一步创建的多边形或者三角形中，在链表中找出外接圆包含插入散点的三角形，删除外接圆的公共边，形成Delaunay空腔。

3)插入的散点连接Delaunay空腔上的顶点，形成新的三角格网。

4)重复步骤2)、步骤3)，直到所有散点插入完毕。

2.5 区域面积求和

根据前面步骤能获取到每个插值点的高度的信息，可以利用海伦公式(3)对三角格网中的每个三角形进行面积的计算。

(3)

其中：a、b、c分别代表三角形三个边的长度；p代表的是三角形的周长。每一个边的边长可以使用欧式距离公式来计算，n维欧式距离表示为式(4)。

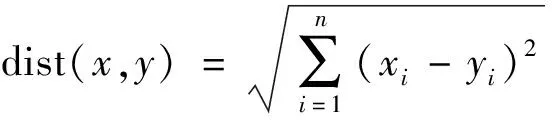
(4)

其中：n表示维度；x、y为在同一维度上的值。最后将三角格网中三角形的面积逐一相加，得到三维地形表面积测量的结果。

3 实例分析

笔者以Cesium.js作为3D WebGIS前端框架，IIS服务器为地形服务提供数据响应，用CesiumLab处理30 m分辨率的DEM数据产生.terrain格式的地形切片数据，以GeoServer为影像地图服务器，本文所有的计算均是由浏览器内核计算，无后台服务器提供计算。实验环境是采用的win10操作系统，Cpu为i5-3470，浏览器是谷歌浏览器。

Cesium是由JavaScript脚本语言编写的前端轻量级开源WebGIS框架，也是开源三维地图引擎。Cesium不需要其他任何浏览器插件支持，只需要浏览器支持WebGL功能即可，并且具有跨平台、跨浏览器的优点[9]。GeoServer是开源地图服务器，能方便用户快速的发布地图影像数据。IIS是由微软公司开发的Web服务程序。

在笔者研发的三维平台上，分别选取地势较为平坦、地势较为陡峭、大面积区域、小面积区域、凸多边形陡峭区域、凹多边形陡峭区域、凸多边形平坦区域、凹多边形平坦区域共计8组相同控制点区域，利用传统的投影方式与本文提出的三维地形面积测量方法来进行实验，以15 m为插值点之间的间距来计算贴地面积。最终实验对比结果见表1。

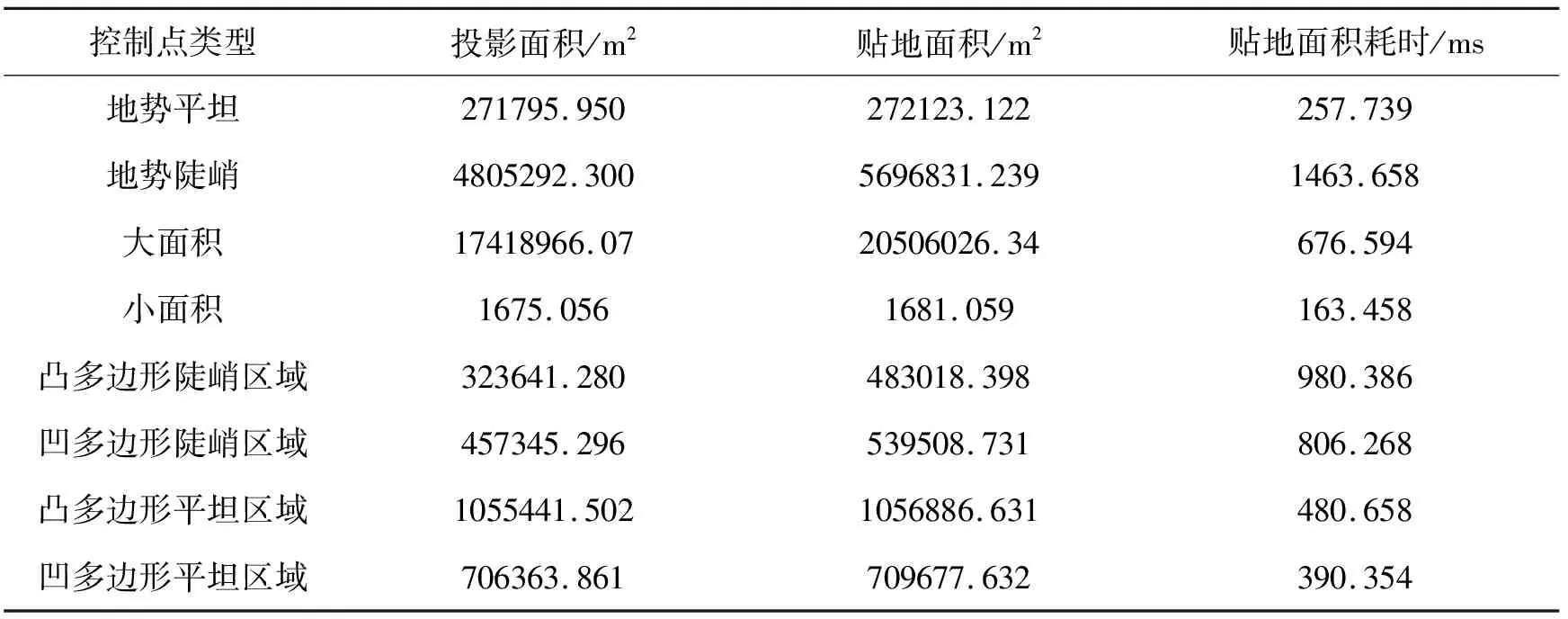
表1 面积测量结果对比分析

实验在地势陡峭区域的投影面积效果图如图3所示，贴地表面积如图4所示，投影面积为4 805 292.3 m2，贴地表面积为5 696 831.239 m2。

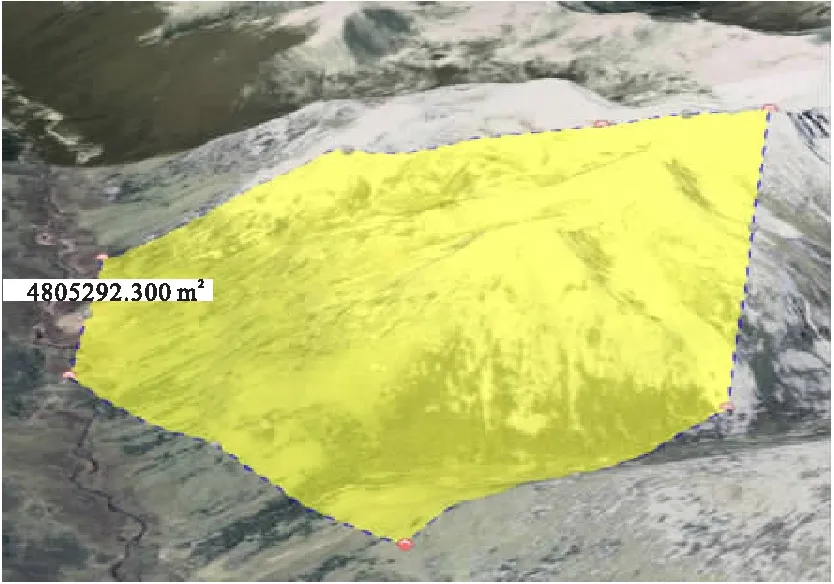
图3 投影面积

图4 贴地面积

由表1可知，在选择同样的控制点的情况下，投影面积始终小于贴地表面积，符合实验的预期结果。在地势较为平坦的情况下，投影面积和贴地表面积相差不是很大，在地势较为陡峭的区域，投影面积和贴地表面积相差较大，这两者从侧面验证了本文提出方法的可靠性。

4 结论

笔者提出了一种基于Web的三维地形表面积测量方法，其具有无需后台服务器计算，依靠浏览器内核计算，同时能够快速嵌入前端的特点。该方法在Cesium库的基础上结合耳切法、Delaunay三角网算法与线性插值构建区域三角网，然后利用海伦公式来求取三维地形表面积。其中耳切法、Delaunay三角网算法具有比较成熟且应用较广的特点，能有效解决三维三角形格网面积的计算。该方法可以辅助人们在地势陡峭难以测量的区域进行测量，例如滑坡面积测量以及露头岩层面积的测量，一定程度上减少了人们到高危险区域的危险性以及费时、费力的局限性，同时也具有高度灵活测量的优点。