基于灵敏度加权的带地形直流电阻率布极方式及2.5D反演研究

李清坤, 曹 辉, 曹礼刚, 邢雯淋, 张朝晖

(成都理工大学 地球勘探与信息技术教育部重点实验室，成都 610059)

0 引言

作为一种高灵活性且实用性的地球物理勘探方法，直流电阻率法常用于各大工程领域中,因此直流电阻率法的正反演研究工作一直备受关注[1-3]。自20世纪70年代以来，有限元法被应用到地球物理正演计算。Coggon[4]提出的方法为有限单元法在地球物理中的应用奠定了正演理论基础；BIBBY[5]在Coggon工作的基础上给出了轴对称体直流电阻率模型计算方法，这大大地增加了直流电法在复杂地形的应用的可能性；Dey等[6]将有限差分方法引入点源二维任意地电剖面电阻率法正演计算中；周熙襄等[7]在Dey等提出的方法上加入了混合边界条件进行正演计算并给出试算结果，提高了正演计算的效率和精度，进一步证明了有限差分法的实用价值；徐世浙[8]在书中详细介绍了对于直流电阻率二维的正演有限元法数值计算过程；底青云[9]运用直流电场有限元方法进行了二维线源正演模拟，探讨了改进复杂结构下的有限元正演模拟的实效性；阮百尧等[10]提出了具有高精度的有限元方法数值解，解决了二维地电断面电阻率测深的变分问题；Greenhalgh等[11]介绍了一种基于高斯正交网格(GQG)的新型电阻率建模方法的理论，可以在具有任意地形条件下对2.5D/3D各向异性模型中计算出电势；汤井田等[12]运用非结构化三角形网格,对起伏地形下2.5D直流电阻率进行正演模拟,并利用比较法来消除地形的影响，获得了良好的效果。

在反演研究中，Loke和Barker[13-14]采用拟牛顿方法对高斯-牛顿方法进行了改进，使得反演的精度得到了保证；阮百尧等[15]提出了一种二维直流电阻率测深的快速反演方法，在实际的生产工作取得了很好的效果；吴小平等[16]采用共轭梯度迭代法，实现了直流电阻率测量数据的三维最小构造反演；Singh等[17]提出了基于神经网络的二维电阻率测深快速优化反演算法，并应用实际的电阻率测深数据反演中，使得数据解释更为快速、高效、准确；冯德山等[18]采用有限单元法对超高密度电法的全四极装置进行正演模拟，采用广义最小二乘正则化反演,较好地刻画出复杂地形条件下的异常体的形态及地下电性的分布；吴小平等[19]基于非结构化四面体网格，采用不完全Gauss-Newton反演法，实现了对任意地形条件下偶极-偶极视电阻率数据的三维反演；周勇等[20]使用了基于模型敏感度信息的非结构化自适应网格算法来生成满足反演要求的高质量网格，并使用了稳定的双共轭梯度法来求解Gauss-Newton方程以实现三维直流电阻率稳定反演法。

笔者在前人研究的基础上，研究了起伏地形条件下直流电阻率2.5D反演算法，为直流电阻率法的数据处理解释提供理论支持。首先，将有限体积法引入二维正演线性方程组中求解，提高了正演数值模拟的精度和速度；然后，将反演中常用的正则化Tikhonov反演思想引入其中，并在反演算法中采用多线程并行计算求解矩阵，大大节省了内存和时间的消耗，最后，对pole-dipole和dipole-pole和dipole-dipole装置的反演效果进行了对比分析。

1 正演算法

假设地下全空间电导率为σ，点电流源位于地表，则满足直流电阻率法的2.5维偏微分方程(PDEs)及其边界条件(BC)公式为式(1)[21]。

(1)

式中：φ为电位向量,V；σ为电导率,S/m；I为供电电流强度,A·m-3；rs+为供电电极正极位置；rs-为供电电极负极位置。在直流电阻率法中，使用接收电极对电位场中的差异进行采样，以收集观测数据。为了模拟该偏微分方程(PDEs)(或一组PDEs，如果存在多个电流源位置)，必须将该方程离散化到计算网格上。

此方程在地表空气边界满足Newman边界条件，在无穷远处满足混合边界条件，通过使用交错网格有限体积法(FVM)，我们将系统离散化为：

(2)

Aφ=-q

(3)

其中

(4)

式中：A为系数矩阵；q为场源向量，采用不完全的LU分解法解方程[22-23]，即可得到电位U和视电阻率值ρs

(5)

其中：ε为接收电极处电位向量；ΔU为电位差；K为装置系数。

2 反演算法

地球物理中反演一直是一项复杂而艰巨的任务，由于反演问题本身就存在多解性和不确定性，基于此笔者采用Tikhonov正则化反演方法[24-26]，建立目标函数为式(6)。

φ(m)=φd(m)+βφm(m)

(6)

式中：φ为正则化因子;φ(m)为数据目标函数项；φm(m)为模型目标函数项。

这里采用基于模型与先验信息mref的最小二范数

(7)

式中：Wm为模型权重，是x、y和z方向上一阶平滑度的矩阵。每个Wm矩阵可以用整数离散表示。正则化Wm是应用为每个单元格具有不同权重的标量或对角矩阵加权总和α*的矩阵。

将数据目标函数写为式(8)[24]。

(8)

式中：Wd为数据的权重矩阵，该矩阵为对角矩阵，其元素为Wdii=1∈i，其中εi是第i个标准偏差；F(m)为正演函数；m为模型参数；d为观测所得的数据。

则其梯度为：

(9)

式中：J[m]为灵敏度矩阵;J[m]ij为第i个基准点相对于第j个模型参数的变化方式；在第k次迭代中，从模型mk开始搜索扰动δm以减少目标函数，可以给出反演模型所需要的公式：

F[mk+δm]≈F[mk]+J[mk]

(10)

求解该扰动，将梯度设为0

(11)

更新的模型由mk+1=mk+γδm给出，其中γ∈(0,1]，该系数可以通过一维搜索找到，其默认值设为“1”。直到达到合适的停止标准方可停止迭代优化过程。反演流程图如图1所示。

图1 反演并行算法流程图

3 灵敏度

对于灵敏度的求解，我们参考文献[24]，直流电阻率法的正演问题为对形如式(12)的偏微分方程进行求解：

c(m,u)=A(m)u-q=0

(12)

其中:m为正演模型；u表示需要求解的场。对于给定的模型m，可以计算出场u(m)，由于求解得到的数据是场的子集，因此可以由线性投影P来从模型中创建投影数据

dpred=Pu(m)

(13)

其中P是字段在数据空间上的投影。

对于反演问题，主要是解决如何通过改变模型来转换数据。将式(13)泰勒展开得式(14)。

O(h2‖v‖)

(14)

根据式(14)，改变模型得到相应反演数据，也是我们所求的解的方程。基于此离散化，我们得出离散化空间中的灵敏度。灵敏度矩阵可以写成式(15)。

J=-PA-1G

(15)

从而可以对偏微分方程(PDE)进行求导

(16)

将式(16)代入式(15)中可以得到灵敏度矩阵为式(17)。

J=-P(uc(m,u))-1mc(m,u)

(17)

4 正确性验证

为了验证该直流电阻率法正演算法的准确性与可行性，设置了一个场源在地面的均匀全空间模型，其电阻率为100 Ω·m。图2为均匀全空间模型偶极装置数值模拟结果，从图3可知，在靠近坐标轴原点区域，解析解与数值计算的结果出入较大，其余计算区域的正演模拟结果与解析解吻合较好，总体平均误差小于0.1%。证明了该正演算法是准确可靠的，可以为反演的模型做进一步地准备。

图2 偶极装置解析解与数值模拟计算结果对比图

图3 解析解与数值模拟计算结果误差图

5 算例分析

5.1 算例一

构建的模型如图4所示,长为200 m，深为60 m，包含高阻和低阻不同形状异常体的二层带地形模型，浅层为1 000 Ω·m的圆形高阻体，异常体的中心坐标(100 m，-20 m)，其半径为10 m；另设两个10 Ω·m的长方形形高阻体，异常体的长为40 m，宽10 m，围岩电阻率为100 Ω·m。网格剖分密度为1 m×1 m，测线沿着X轴方向布设20个供电电极，测点布设间隔为10 m。AB极距为10 m，MN极距为10 m。

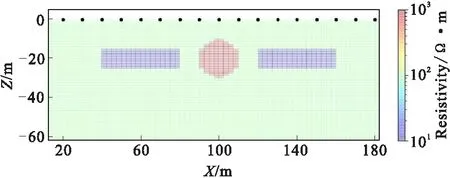
图4 平地形模型

如图3建立的数值计算模型，进行直流电阻率法的四极和三极装置进行正演数值计算。首先对模型分别采用偶极-偶极(dipole-dipole)、单极-偶极(pole-dipole)、偶极-单极(dipole-pole)、三种布极方式，对构建的模型进行直流电阻率法正演计算，得到视电阻率拟剖面(图5)。可以看到，dipole-dipole方式能较好分辨出高阻体和低阻体的存在，pole-dipole和dipole-pole方式虽能反映出分别存在高低阻体，但对于埋深和方位的理解存在较大偏差。

图5 视电阻率拟剖面

图6为视电阻率直方图。由图6可以看到，三种布极方式描述的视电阻率直方图能够较好地反映出视电阻率的集中分布情况，对于高阻体的存在给出了明确的信息，但对于低阻体的反映则不明显。

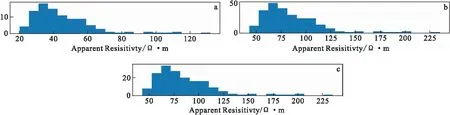
图6 视电阻率直方图

采用灵敏度加权反演后，得到灵敏度如图7所示。由图7可以看到，三种布极方式对于浅层有着较高的灵敏度，随着地层变深而灵敏度降低，当存在高阻体时，灵敏度存在较明显地降低，而存在低阻体时，灵敏度降低相对周围围岩存在明显地变缓。

图8为恢复电导率反演结果，图8中黑色实心倒三角为布设的20个电极。本次通过建立模型进行数值模拟，正演过后的视电阻率带入反演算法中，通过对比反演成像之后的结果图与原始模型可以发现，建立的模型与反演结果吻合得很好，证明了本文算法的可靠性。可以看到，对于高阻体，三种布极方式均能正确反演出来，其中dipole-dipole方式反演结果较为理想。而对于pole-dipole和dipole-pole低阻体则在图8反演图中可以看出，对低阻体的形态有所偏差。在平地形模型下，dipole-dipole装置的视电阻率异常也是明显大于三极装置的视电阻率异常，dipole-dipole装置的分辨率比pole-dipole和dipole-pole装置的分辨率高。

5.2 算例二

异常体组合模型的三个电阻率分别是1 000 Ω·m、10 Ω·m和1 000 Ω·m。背景电阻率为均匀介质值为100 Ω·m，图9为起伏地形电阻率模型。在凹地形的一侧埋有1 000 Ω·m的条形高阻体。长为60 m，宽为10 m，另一侧凸地形同样埋深条形高阻体，中间设有一个10 Ω·m的圆形低阻体。对比图11三种装置的反演结果图，从这三个装置的反演结果，可以看出三种布极方式都可以准确地反映异常体的埋藏深度和形态。通过比较不难发现dipole-dipole装置反演得到的异常幅值大小以及边界范围与真实模型更为贴近。对于低阻体的刻画相对于diploe-pole和pole-dipole更为真实准确。

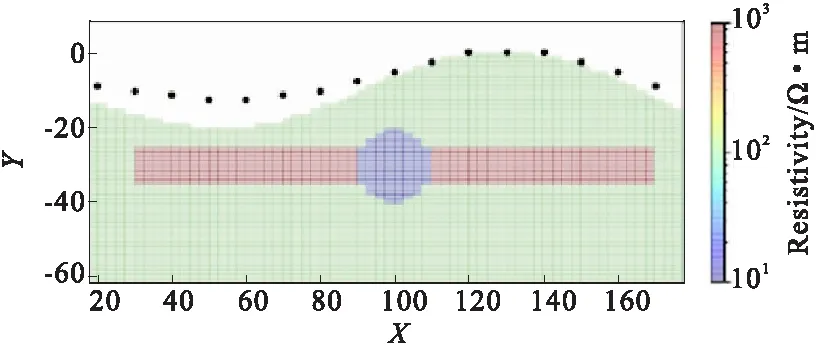
图9 起伏地形电阻率模型

图10 灵敏度分析

图11 反演结果

图10表明在相同的条件下，dipole-dipole装置比pole-dipole和dipole-pole装置对异常体更灵敏，异常响应明显较大。在近地表对异常的响应，dipole-dipole装置相对比pole-dipole和dipole-pole装置更为集中，主要表现为富集在地表能量的响应更强。结合图8与图11可以看出，地形对三种布极方式的影响会使得装置对地下异常体的形态变形，从而产生假的异常给后续的解释带来困难，dipole-dipole装置反映异常的能力均强于pole-dipole和dipole-pole装置，且随着地表场源的位置靠近异常体，dipole-dipole装置的异常幅值明显增大，而pole-dipole和dipole-pole装置的异常幅值相对较小，在凹地形异常体埋深较浅，三种布极方式对异常体的形态都可以较为明显刻画出来，在凸地形中由于异常体的埋深较深，dipole-dipole相对于pole-dipole和dipole-pole表现更为出色，对起伏地形中低阻异常体也可以看出，dipole-dipole具有更好的分辨率以及对异常体形态的刻画更为准确。

6 结论

基于前人的基本理论，利用有限体积法对起伏地形的直流电阻率法进行正演，计算出大小相同，位置、电阻率不同的高阻和低阻圆形异常体的视电阻率值。利用加权正则化Tikhonov反演方法实现起伏地形2.5D电阻率反演成像算法，模型计算结果表明，该反演算法较稳定、快速，反演结果良好；在正演算法中，利用多线程并行计算大型稠密矩阵，为反演算法中快速回代求解提供了条件；反演算法中构建了带地形和高、低阻异常体的二层模型，实现了灵敏度加权的2.5D反演方法，研究了直流电阻率法三种布极方式对反演结果的影响，得出结论不同的布极方式对地下导体反演的效果不同，三种布极方式反演结果表明，dipole-dipole装置对地下异常体的响应更为明显，探测的能力更好，分辨率也同样比dipole-pole、pole-dipole两种布极方式要好。