空间动力装置用内可逆Brayton循环功率优化
2022-03-24戈延林陈林根冯辉君
王 倓 ,戈延林 ,陈林根 ,冯辉君
(1.武汉工程大学 热科学与动力工程研究所,武汉 430205;2.湖北省绿色化工装备工程技术研究中心,武汉 430205;3.武汉工程大学 机电工程学院,武汉 430205)
自有限时间热力学(Finite Time Thermodynamics,FTT)理论用于不同的热力装置研究以来,相关研究取得了一系列成果[1-7]。由于闭式Brayton循环有着功率密度大、工作性能稳定等特点,众多学者以经典热力学[8-10]和有限时间热力学[11-15]理论分析和优化了闭式Brayton循环的性能。
与地面用的热力系统相比,空间用的热力系统呈现出一系列新特点[16-23]:由于太空中环境温度比较低,低温热源产生的废热须经由专门的散热器与环境进行辐射换热,以提高循环的输出功率;为提高空间动力装置的输出功率,需要在较短的时间内将最多的废热投射到空间环境,这就需要辐射体与空间环境的温差比较大,并要求有更大的散热面积,但前者意味着更小的热电转换效率,后者意味着更大的质量。为了保证整个装置具有足够的输出功率,就需要更大的反应堆,这进一步恶化了循环乃至整个空间动力装置的质量特性。
众多学者研究了如何提高空间动力装置的性能,他们以闭式Brayton循环为基础,用经典热力学[16-19]和FTT[20-23]理论分析和优化了空间闭式Brayton循环的性能。Barrett[16-17]对核空间闭式Brayton循环的换热器的设计和模型的保真性进行了研究,为空间动力装置的设计提供了最低的保真度;Liu等[18]对闭式Brayton循环空间动力装置的性能进行了优化研究,通过优化系统组件的关键参数使动力装置的总质量最小;Toro等[19]分析了空间闭式Brayton循环在不同工质空间运行情况下主要运行参数对功率和效率与散热器面积比关系的影响;文献 [20-23]基于低温热源和环境之间的传热服从辐射传热规律,建立了核空间闭式简单和回热式Brayton循环模型,并给定高、低温热源之间换热器的热导率来预测能量转换性能,分析了换热器热导率对动力装置功率和效率的影响。此外还有学者对其他空间动力装置热力循环的性能进行了优化[20],Toro等[19]用经典热力学理论分析了斯特林和朗肯循环在不同工质空间运行情况下主要运行参数对功率和效率与散热器面积比关系的影响。
本文将运用FTT理论,建立仅考虑热阻损失的空间用内可逆闭式Brayton循环模型,首先给定高温侧和中间侧换热器的有效度,分析循环各参数对功率最优性能的影响;然后给定整个装置3个换热器的总热导率,以功率作为优化目标对换热器热导率分配进行优化,得到循环的最大功率,进一步优化低温热源温度,得到了二次功率最大值,分析高温热源温度、换热器总热导率和空间环境温度对循环性能的影响,所得结果对实际空间动力装置的设计优化有一定指导作用。
1 循环模型和性能分析
图1为空间用内可逆Brayton循环T-s图,图中1→2和3→4是两个绝热过程,2→3和4→1是两个等压过程,2→3为工质从高温热源吸热的过程,4→1为工质向低温热源放热的过程(TH和TL分别为高、低温热源温度)。设压气机和涡轮机中实现理想的能量转换,即ηc=ηf=1。空间用内可逆Brayton循环除了在工质与热源之间采用热管式换热器外(工质吸热和放热过程分别通过高温侧和中间换热器完成),还需要在低温热源与空间环境之间采用辐射散热器,用于向空间散热。
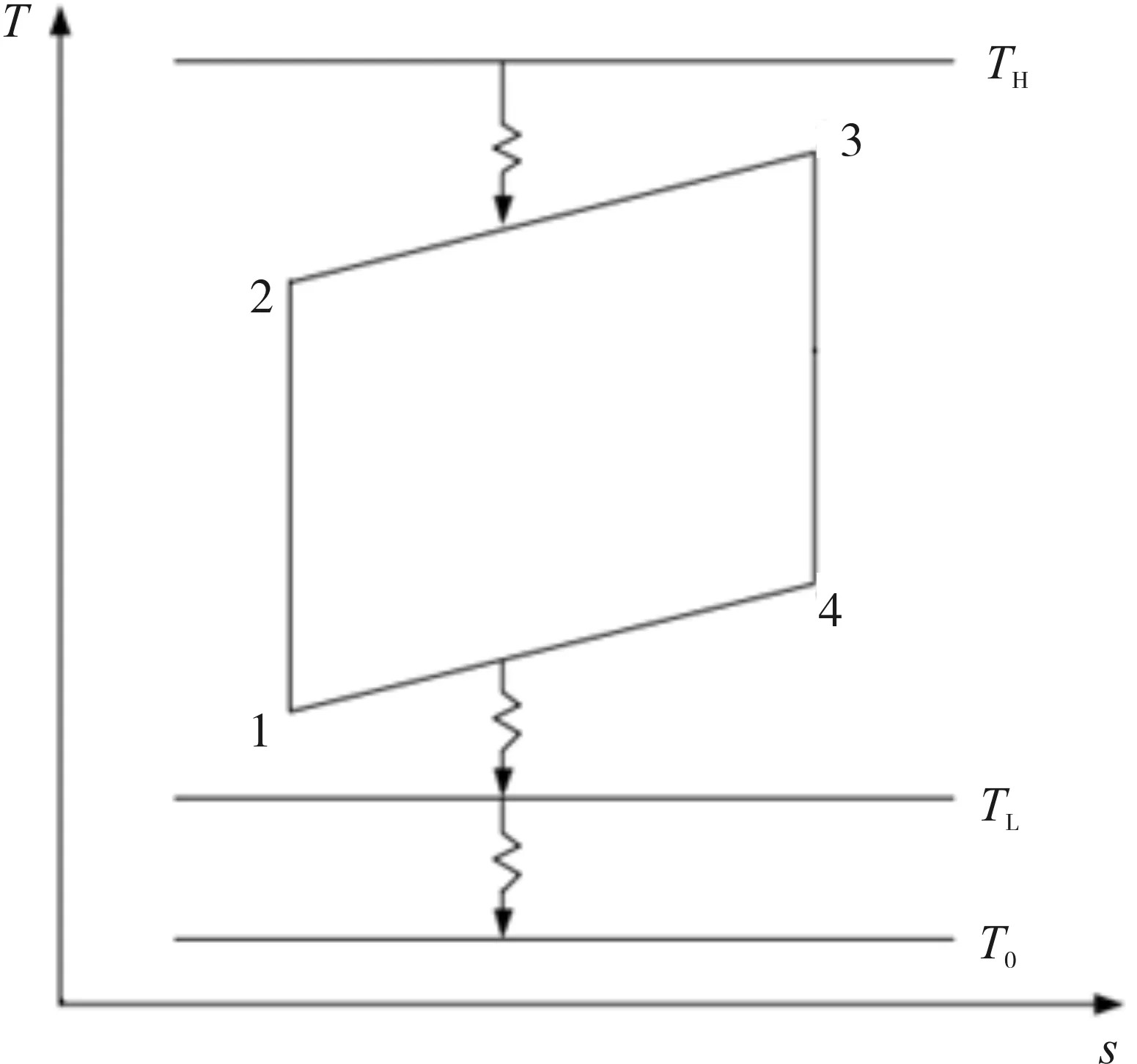
图1 空间用闭式Brayton循环T-s图
工质热容率为Cwf,高温侧和中间换热器热导率分别为UH和UL。由工质的性质和换热器理论可得循环的吸、放热率分别为:
Q1=Cwf(T3-T2)=CwfEH(TH-T2)
(1)
Q2=Cwf(T4-T1)=CwfEL(T4-TL)
(2)
式中:EH和EL分别为高温侧和中间换热器的有效度。二者可以分别写为:
EH=1-exp(-NH)
EL=1-exp(-NL)
(3)
式中:NH和NL分别为高温侧和中间换热器的传热单元数。二者可以分别写为:
NH=UH/Cwf,NL=UL/Cwf
(4)
根据内可逆条件,循环4个温度间的关系为:T1T3=T2T4。定义压气机的压比为π,则有:
(5)
式中:m=(k-1)/k,k为绝热指数。
散热器把来自中间换热器的热量辐射到空间环境,热导率(黑度系数ε与辐射体面积Ar的乘积)为UR,其辐射散热的热流率为:
(6)
式中:σ为Boltzmann常数;ηf为翅片效率;T0为空间环境温度。
由式(1)和(2)分别可得:
T3=(1-EH)T2+EHTH
(7)
T1=(1-EL)T4+ELTL
(8)
由式(5)、(7)和(8)可得:
T2π-m=(1-EL)T4+ELTL
(9)
T4πm=(1-EH)T2+EHTH
(10)
由式(9)可得:
(11)
由式(2)和(10)可得:
(12)
由热力学第一定律可得:
Q2=Q3
(13)
即:
(14)
由式(14)可得:
(15)
由式(15)可得:

(EH-EL(EH-1))]-1
(16)
将式(16)代入式(11)可得:

(17)
将式(15)和(17)分别代入式(1)和(2)可得:

(CwfEL)]+TL}-1·
[EH-EL(EH-1)]-1}
(18)
(19)
循环输出功率和热效率分别为:
P=Q1-Q2
(20)
η=P/Q1
(21)
2 数值计算与分析
2.1 换热器热导率给定时循环性能分析
根据文献[14-15,23]确定相关参数:σ=5.67×10-11kW/(m2·K4);ηf=0.9,Ar=122.4 m2;EH=EL,为0.7~0.9;T0=190~210 K;TH=1 100~1200 K;Cwf=1.0;k=1.4。
图2至图5给出了高温侧换热器、中间换热器和辐射体散热器热导率给定情况下,TH和T0对Pmax-TL、Pmax-π的影响。由图2和图3可知:P-TL、P-π曲线均呈类抛物线型,即存在一个最佳的低温热源温度TLopt(或者最佳压比πopt)使循环达到最大功率Pmax。计算还表明,P-η的曲线也呈类抛物线型。
图2和图3给出了高温热源温度TH对P-TL和P-π性能特性的影响。由图2和图3可知,随着TH的增加,Pmax、TLopt和压比πopt均增加,数值计算表明,当TH从1 100 K增加到1 200 K时,Pmax从128.092 kW增加到153.79 kW,增加了约20.1%;TLopt从407.2 K增加到418.8 K,增加了约2.8%;πopt从9.61增加到10.13,增加了约5.4%。计算还表明,随着TH的增加,Pmax对应的效率ηP也增加。当TH从1 100 K增加到1 200 K时,ηP从0.468增加到0.484,增加了约3.4%。
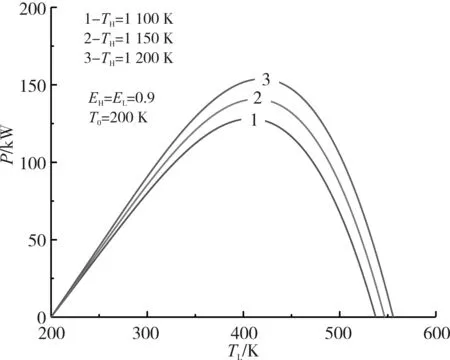
图2 TH对循环P-TL特性的影响

图3 TH对循环P-π特性的影响
图4和图5给出了环境温度T0对P-TL、P-π特性的影响。由图4和图5可知,随着T0的降低,Pmax增加,而TLopt和πopt减少,数值计算表明,当T0从210 K减少到190 K时,Pmax从140.14 kW增加到141.26 kW,增加了约0.8%;TLopt从414.39 K减少到了411.8 K,减少了约0.63%;πopt从9.73减小到9.68,减小了约0.6%。计算还表明,随着T0的降低,ηP增加。当T0从210 K减少到190 K时,ηP从0.475增加到0.478,增加了约0.63%。

图4 T0对循环P-TL特性的影响

图5 T0对循环P-π特性的影响
由数值计算还可得到高温侧和中间换热器有效度EH和EL对P-TL、P-π和P-η性能特性的影响。计算表明,当EH=EL时,随着EH和EL增加,Pmax和TLopt均增加,ηP和πopt减小。数值计算表明,当EH和EL从0.6增加到0.9时,Pmax从90.243 kW增加到140.74 kW,增加了56%;ηP从0.506减小到0.476,减小了约6%;TLopt从362.4 K增加到413.2 K,增加了约14%;πopt从11.83减小到9.61,减小了约18.8%。计算还表明,当EH≠EL时,随着EL的增加,Pmax和TLopt均增加,而ηP和πopt减少。当EL从0.6增加到0.9时,Pmax从109.25 kW增加到140.74 kW,增加了约28.8%,ηP从0.494减少到0.476,减少了约3.6%,TLopt从382.9 K增加到413.1 K,增加了约7.9%,πopt从10.86减小到9.61,减小了约11.5%。
2.2 换热器热导率分配优化
以功率为优化目标,通过给定高温侧换热器、中间换热器以及辐射体散热器热导率之和,即UT=UH+UL+UR,对换热器和散热器的热导率分配进行优化。定义换热器和散热器的热导率分配以及热导率需要满足的约束关系分别为:
uiii=Uiii/UT(iii=H,L,R)
(22)
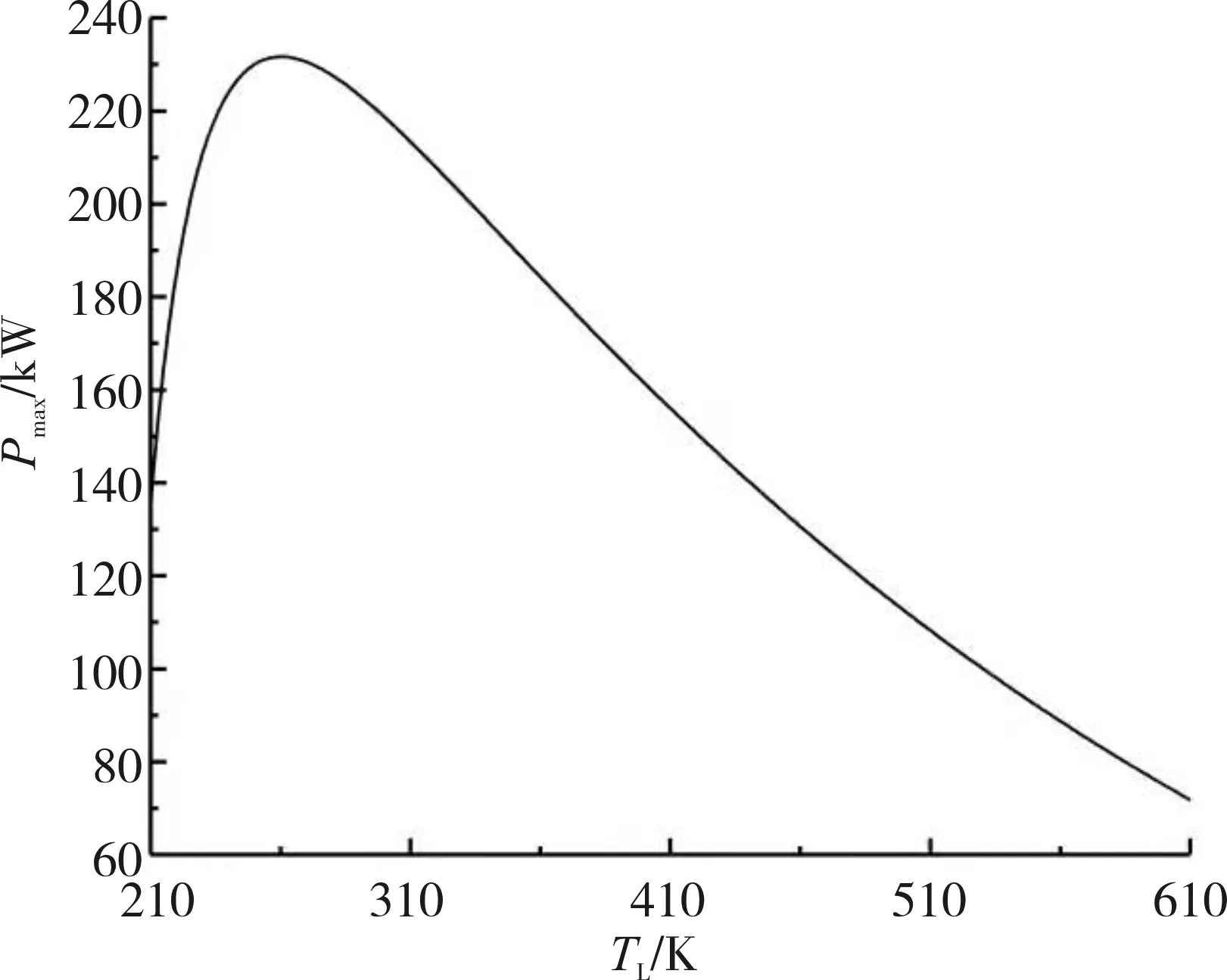
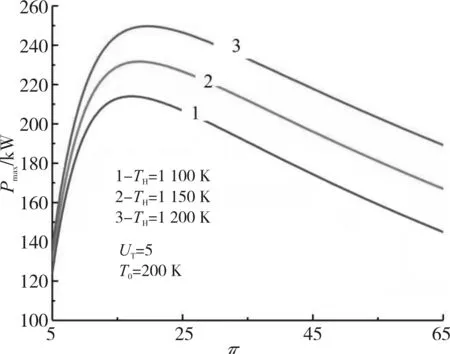
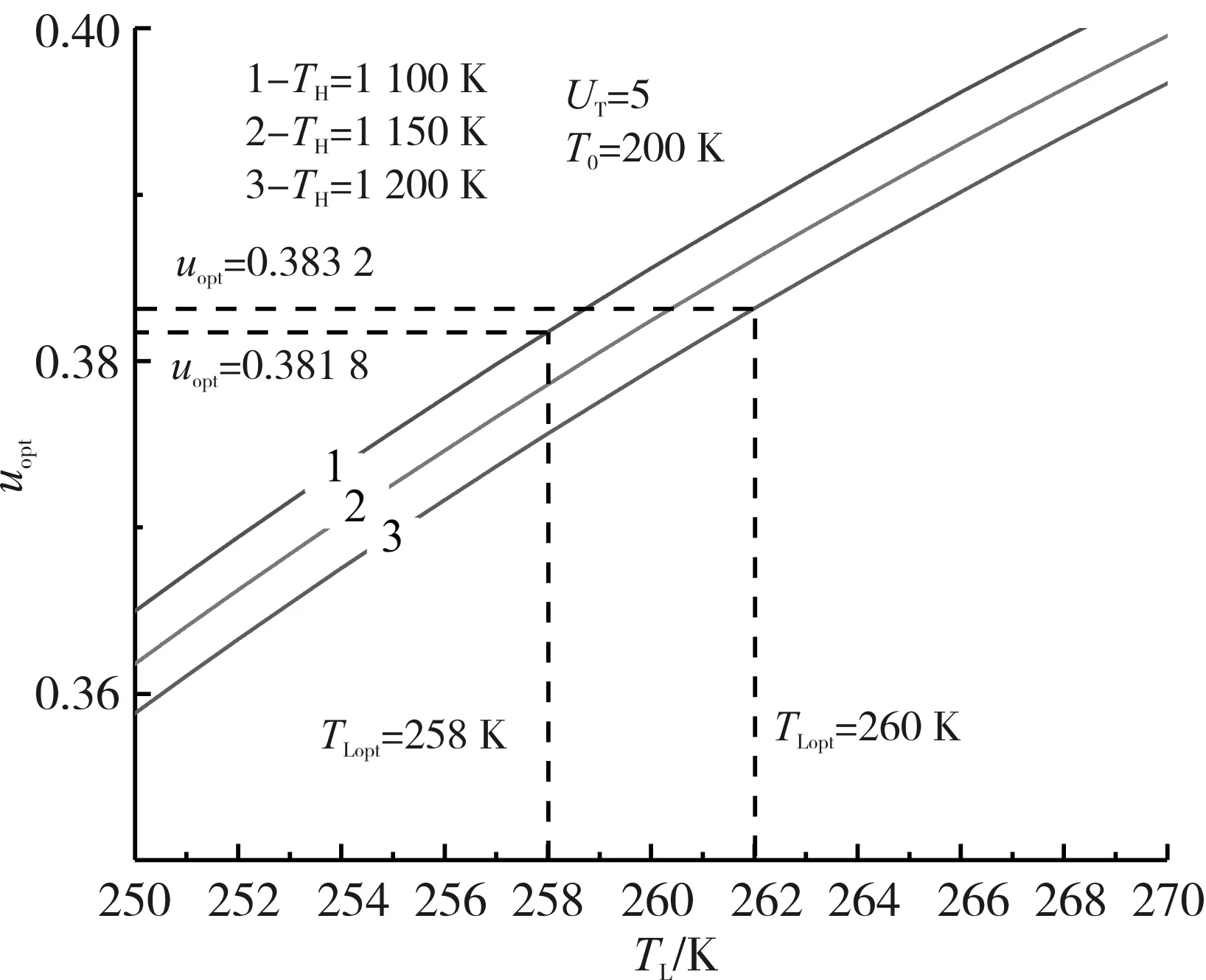
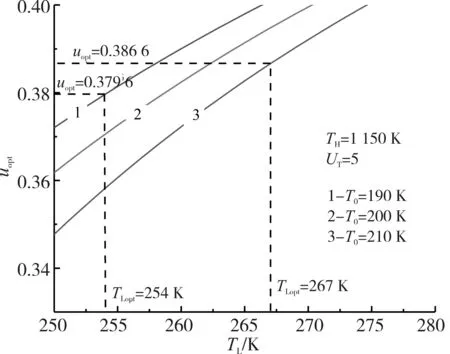
∑uiii=1,0 (23) 本文对功率的优化结果采取数值计算的方式,相关参数取值与2.1节相同,给定换热器总热导率UT为3~9 kW/K。 图6和图7给出了UT=5 kW/K、TH=1 150 K、T0=200 K时,功率与高温侧和中间换热器热导率分配uH和uL以及最大功率Pmax与低温热源温度TL的关系。从图6中可以看出,随着uH、uL的增大,功率P呈现先增大后减小然后逐渐趋于平稳的类抛物线型变化。对于一定的低温热源温度,存在一个uHopt和uLopt使得功率最大,达到Pmax,同时对于一定的热导率分配uH和uL,存在一个低温热源温度TLopt也使得功率最大,达到Pmax,因此同时存在一对最佳低温热源温度TLopt和最佳热导率分配uHopt和uLopt,使得功率达到二次功率最大值,即Pmax,max。 图6 P与uH和uL之间的关系 图7 Pmax与TL之间的关系 图8至图11分别给出了TH、UT和T0对Pmax-π和uopt-TL(uopt=uHopt=uLopt)的影响。高温侧、中间换热器热导率的最佳分配随着低温热源温度的增加而增加;最大功率与压比的关系曲线呈类抛物线型。计算还表明,最大功率与效率的关系曲线也呈类抛物线型。 图8和图9分别给出了UT=5 kW/K,T0=200 K时,高温热源的温度TH对Pmax-π和uopt-TL的影响。随着TH的增加,Pmax,max、TLopt、uopt的压比πopt均增加。当TH从1 100 K增加到1 200 K时,Pmax,max从214.0 kW增加到了249.66 kW,增加了约16.7%;uopt从0.381 8增加到0.383 2,增加了0.37%;πopt从17.16增加到19.76,增加了15.2%;TLopt从258 K增加到262 K,增加了1.6%。计算还表明,随着TH的增加,ηPmax增加。当TH从1 100 K增加到1 200 K时,ηPmax从0.556增加到0.591,增加了6.3%。 图8和图9分别给出了TH=1150 K,T0=200 K时,UT对Pmax-π和uopt-TL的影响。随着UT的增加,Pmax,max和πopt增加,而uopt和TLopt减少。当UT从3 kW/K增加到9 kW/K时,Pmax,max从158.38 kW增加到310.12 kW,增加了约95.8%;uopt从0.396 6减少到0.348 9,减少了12%;πopt从17.49增加到19.71,增加了12.7%;TLopt从273 K减少到239 K,减少了12.5%。计算还表明,随着UT的增加,ηPmax增加。当UT从3 kW/K增加到9 kW/K时,ηPmax从0.559增加到0.573,增加了2.5%。 图8 TH对循环Pmax-π特性的影响 图9 TH对循环uopt-TL特性的影响 图10和图11分别给出了TH=1 150 K,UT=5 kW/K时,T0对Pmax-π和uopt-TL的影响。随着T0的减少,Pmax,max和πopt增加,而uopt和TLopt减少。当T0从210 K减少到190 K时,Pmax,max从227.84 kW增加到235.27 kW,增加了约3.3%;uopt从0.386 6减少到0.379 6,减少了1.8%;πopt从17.21增加到19.59,增加了13.8%;TLopt从267 K减少到254 K,减少了4.9%。计算还表明,随着T0的减少,ηPmax增加。当T0从210 K减少到190 K时,ηPmax从0.556增加到0.573,增加了3.1%。 图10 T0对循环Pmax-π特性的影响 图11 UT对循环uopt-TL特性的影响 本文运用FTT理论,建立了仅考虑热阻损失的空间用内可逆闭式Brayton循环模型,导出了循环功率和热效率与低温热源温度的表达式,对循环的功率进行了分析和优化。结果表明: 1)对于一定的低温热源温度,存在一组uHopt和uLopt使得功率最大,达到Pmax,同时对于一定的热导率分配uH和uL,存在一个TLopt也使得功率最大,达到Pmax,因此存在一组最佳TLopt、uHopt和uLopt,使得功率达到二次最大值Pmax,max; 2)随着高温热源温度TH的增加,Pmax,max及其对应的uHopt(或者uLopt)、TLopt、ηPmax和πopt增加;随着高温热源温度T0的减少,Pmax,max、ηPmax和压比πopt增加,而Pmax,max对应的uHopt、uLopt和TLopt减少; 3)随着UT的增加,Pmax,max及其对应的效率ηPmax和压比πopt增加,而Pmax,max对应的uHopt、uLopt和TLopt减少。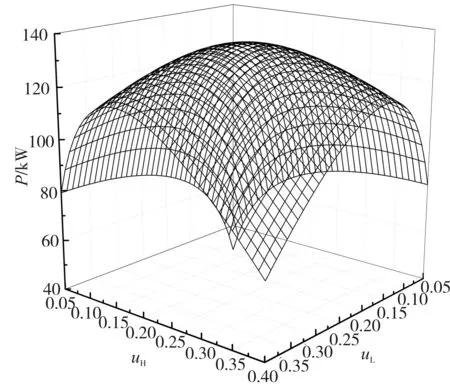

3 结 论
