非对称调制下物理层网络编码系统设计及性能分析

方太彬，唐 猛，陈庆豪，陈建华，曾国峰

(云南大学 信息学院，云南 昆明 650500)

网络编码（Network Coding，NC）[1]技术通过在中继节点对信息进行比特异或以提高系统的吞吐量. 物理层网络编码（Physical-layer Network Coding，PNC）[2]技术是在NC 技术的基础上，根据电磁信号的叠加特性提出的，PNC 系统的吞吐量相比NC系统提升了50%.

在实际的双向中继通信系统中，上下行阶段的信道条件处于动态变化中，为了提升系统数据传输的可靠性等性能，需要随着信道条件的变化调整系统的通信方案. 文献[3-6]基于非对称信道条件，提出了异构物理层网络编码方案，源节点根据信道条件和信息交换的业务负载比例选择不同的调制方式进行数据传输，可改善系统的误码率性能. 文献[7]提出了基于可变QAM 调制的PNC 系统，设计了两阶段搜索算法实现最优映射，从而得到较低的误码率. 文献[8]提出了双正交物理层网络编码方案，在中继节点采用正交组合，提高了非对称通信系统的传输可靠性. 文献[9-11]提出了基于分层调制的物理层网络编码方案，确保在各种信道条件下系统的高速率传输和可靠性. 文献[12]在莱斯衰落信道中，推导出了4/16-QAM 分层调制下PNC系统的平均符号差错率的解析表达式，减少中继节点的欧式距离计算的数量，系统吞吐量得到提升.文献[13]在非对称调制的物理层网络编码系统中，提出了一种聚类最大化算法和标记约束策略，有效降低译码错误概率，提高中继的解码转发性能. 当叠加星座点不满足排他律和标记约束时，启发式最近邻去噪映射算法表现较差.

针对非对称双向中继信道（Two-Way Relay Channel，TWRC），通过调整系统源节点两端的功率分配方案能够有效改善系统性能. 文献[14]提出了将分层调制技术、低密度奇偶校验（Low-Density Parity-Check，LDPC）码、功率优化策略与PNC 技术联合进行研究，提升了整个系统的通信性能. 文献[15]在物理层网络编码系统中提出了自适应功率分配方案，在上行阶段，最大化中继节点接收的网络编码符号的欧氏距离，在下行阶段，中继节点以源节点间的最小互信息最大化为目标函数，使用窄范围方法选择最佳的天线组，并根据算法分配功率，该方案虽然改善了系统误码率性能，但增加了系统的复杂度.

基于非对称信道，本文构建了正交相移键控（Quadrature Phase Shift Keying，QPSK）和二进制相移键控（Binary Phase Shift Keying，BPSK）联合调制的物理层网络编码系统模型，设计了系统中继节点的解调映射规则和译码映射算法. 在实验中对PNC 系统在不同功率分配比下的性能进行分析，得到最优功率分配方案. 实验仿真结果表明，在最优的功率分配比下，联合LDPC 码的非对称调制PNC 系统能够有效改善信号传输的误码率性能.

1 系统模型

1.1 非对称双向中继信道模型 本文基于3 节点双向中继通信系统展开研究，系统通信过程包括上行阶段和下行阶段，节点包括2 个源节点A、B 和1 个中继节点R. 而在实际通信场景中，系统的信道条件是动态变化的，根据信道条件不相等的情况，可分为阶段非对称、下行非对称、上行非对称以及节点非对称[16].

本文以上行非对称信道为例展开分析. 如图1所示，在上行非对称通信模型中，上行阶段节点A到中继R 和节点B 到中继R 两条信道的噪声不同，即nAR≠nBR，其中nAR、nBR分别为节点A、B 到中继R 的信道噪声. 下行阶段的信道条件完全相同，即中继R 到节点A、B 间的信道噪声均为nR. 文中假定上行阶段节点A 到中继R 的信道条件较优，采用QPSK 调制，节点B 到中继R 的信道条件较差，采用BPSK 调制，即QPSK-BPSK 调制. 下行阶段的信道条件较优，采用QPSK 调制进行实验仿真.

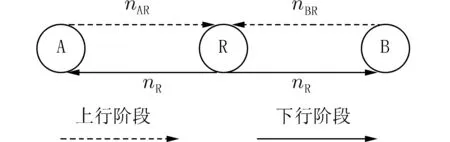
图1 上行非对称通信模型Fig. 1 Uplink asymmetric communication model

在上行非对称通信模型中，各节点的调制星座图如图2 所示. A 节点初始信息流的每个符号含有2 个比特{00，01，10，11}，经QPSK 调制后得到{1+i,1-i,-1+i,-1-i}，其星座图如图2（a）所示；B 节点初始信息流的每个符号只含有1 个比特{0，1}，经BPSK 调制后得到{1，-1}，其星座图如图2（b）所示；A、B 节点的初始信息流通过理想信道后在中继R 叠加后的星座图如图2（c）所示.

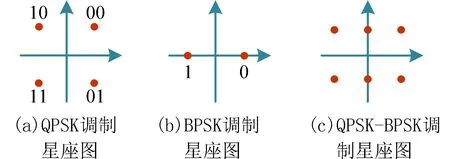
图2 星座图Fig. 2 constellation maps

通信系统两端采用不同的调制方式时，中继R 将调制后的信息流进行叠加，对叠加结果进行解调映射，然后通过广播发送到目的节点. 在下行阶段，目的节点按照设计的规则进行比特异或，实现通信系统两端的信息交互.

1.2 QPSK-BPSK 调制下联合LDPC 码的PNC 系统模型 在双向中继通信系统中，基于QPSKBPSK 调制的物理层网络编码系统联合LDPC 码的上、下行阶段模型框图分别如图3 和图4 所示.

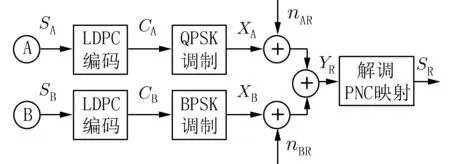
图3 上行通信阶段Fig. 3 Uplink stage

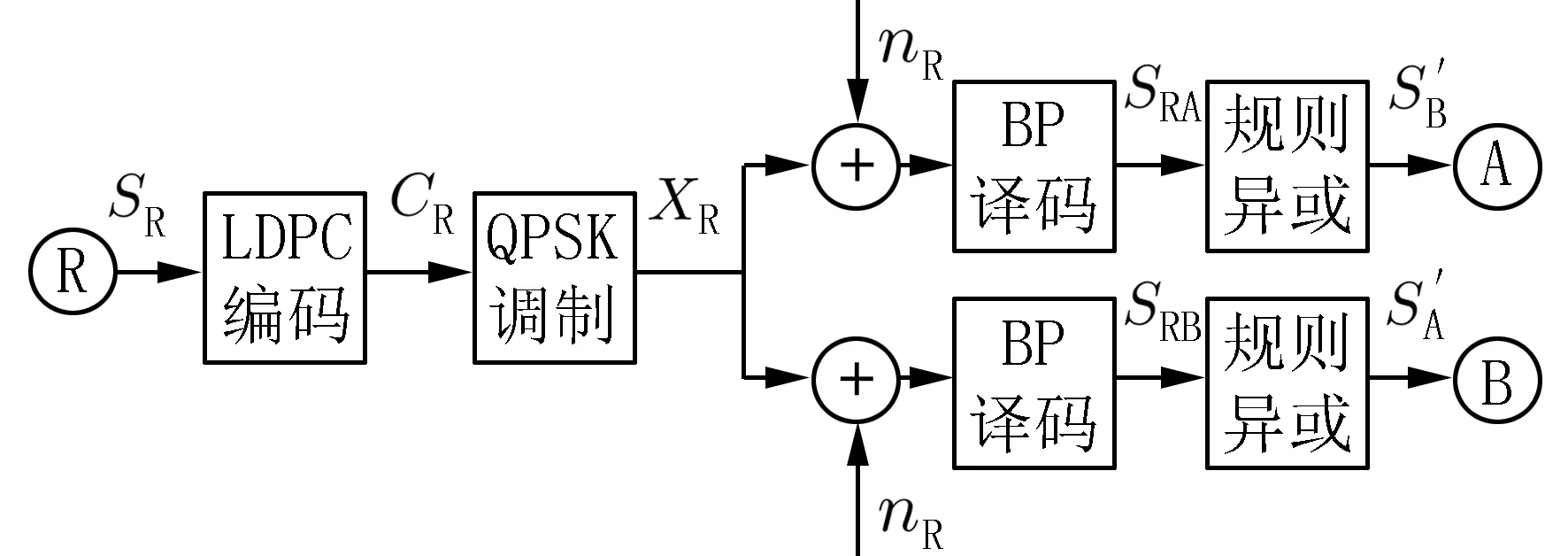
图4 下行通信阶段Fig. 4 Downlink stage

上行阶段：节点A、B 分别将信息长度为2K和K的初始信息流SA∈{0,1}2K和SB∈{0,1}K与K×N维的生成矩阵相乘，进行LDPC 编码，即可得到信息长度为2N和N的信息流CA∈{0,1}2N和CB∈{0,1}N. 根据调制方式的星座图，节点A 将CA∈{0,1}2N→CA∈{00,01,10,11}N，再 对CA进 行QPSK 调制，得到XA∈{1+i,1-i,-1+i,-1-i}N；节点B 的信息流CB经BPSK 调制后得到XB∈{1,-1}N.XA和XB通过加性高斯白噪声信道传输至中继R，中继R 收到的信息流YR为XA、XB和信道噪声的叠加，即：

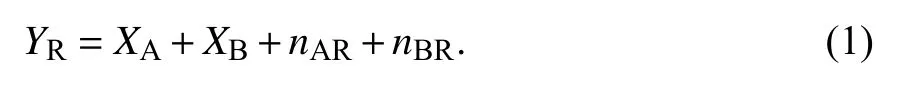
中继R 将接收到的叠加值YR采用对数似然比置信传播（Log Likelihood Ratio Belief Propagation，LLR-BP）算法进行译码，得到映射结果SR∈{0,1,2,3}2K.

2 系统中继映射方案

矩阵M与矩阵G中的值为一一对应关系，并根据行列坐标形成映射关系. 即当中继接收的值为-j时，得到矩阵M中对应-j的行列坐标（1，4）、（2，2），然后得到矩阵G中相应位置的值G（1，4）=G（2，2）=3，从而实现映射关系.

中继R 得到叠加结果后，根据最小距离算法划分判决区域. 首先计算中继收到的实际叠加信息与矩阵M中每个值的欧式距离，得到其中的最小值，将叠加值判决为欧氏距离最小值在矩阵M中所对应位置的值，得到对应值在矩阵M中的行列坐标 (m,n)（m=1,2；n=1,2,3,4），然后根据行列坐标与矩阵G进行映射，得到唯一确定的PNC 映射值.

在下行阶段，由于系统两端交换的初始信息流长度不相等，因此需要在目的节点设计相应的规则将解调映射结果与初始信息流进行比特异或得到交换信息，实现系统两端的信息交互.

A 节点：初始信息流的奇数位和PNC 映射值的奇数位进行比特异或得到交换信息.

B 节点：初始信息流和PNC 映射值的奇数位进行比特异或得到交换信息的奇数位；PNC 映射值的偶数位与0 进行比特异或得到交换信息的偶数位.

2.2 系统在不同功率分配比下的分析 针对上行非对称通信模型，为充分发挥PNC 系统的性能优势，减少系统功率浪费，带功率分配的QPSK-BPSK调制PNC 系统在中继R 接收到的叠加值为：

同理，矩阵M′与矩阵G中的值为一一对应关系，并根据行列坐标形成映射关系，再根据最小距离算法划分判决区域，得到带功率分配的PNC 系统中继解调映射方案.

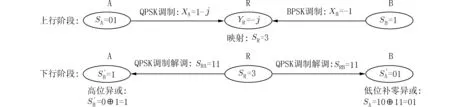
图5 QPSK-BPSK 调制PNC 系统实例Fig. 5 An example of the QPSK-BPSK-PNC system

2.4 QPSK-BPSK 调制下联合LDPC 码的PNC 系统译码算法 在QPSK-BPSK 调制PNC 系统中引入LDPC 码只会改变初始信息流的长度，不会改变其结构. 同理，根据表1 中的实部信息与高位信息、虚部信息与低位信息一一对应的关系，可以得到QPSK-BPSK 调制下联合LDPC 码的PNC 系统中继节点的译码映射方案. 根据映射方案可以将式（1）表示为复数形式，即：

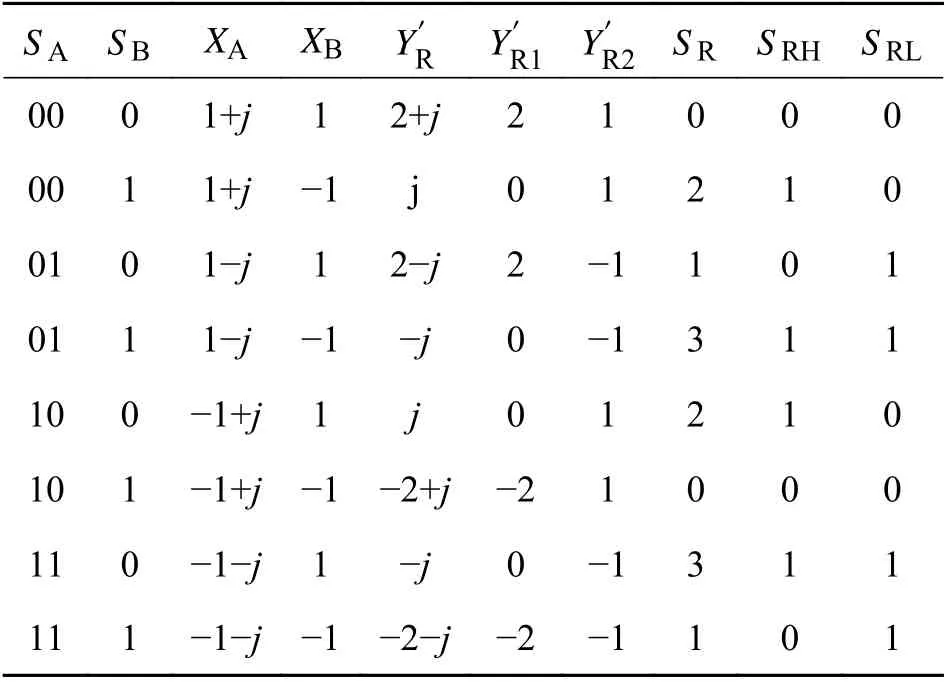
表1 非对称调制下PNC 系统中继映射方案Tab. 1 The relay mapping scheme of PNC system under asymmetric modulation

中继接收值的实部信息YR1与A、B 节点的初始信息流都相关，而中继接收值的虚部信息YR2与B 节点的初始信息流不存在相关性，只与A 节点的初始信息流相关. 因此在上行阶段进行编码时，需要将A 节点的初始信息流分为奇数位和偶数位两路信号，分别进行LDPC 编码，然后合成一路信号进行调制，再与B 节点处理后的信息在中继R 进行叠加，以保证中继接收值与初始信息流的相关性.

中继R 得到叠加信息后，由于系统采用非对称调制，使用LLR-BP 算法进行译码时，需要根据中继接收值与初始信息流的相关性，分别计算中继接收值实部和虚部的初始软信息.

根据文献[17-18]，在加性高斯白噪声信道中采用LLR-BP 译码算法，实部YR1的初始软信息为：

在下行阶段，对PNC 映射值进行LDPC 编码、QPSK 调制后，通过广播发送到目的节点，并对接收到的信息流进行LLR-BP 译码，此时目的节点端的初始软信息与中继接收值虚部的初始软信息相等，将初始软信息输入译码器后得到译码映射结果SRA、SRB， 其中SRA为节点A 收到的信息，SRB为节点B 收到的信息.

在系统中引入LDPC 码同样不会影响目的节点接收映射结果. 同理，在下行阶段QPSK-BPSK调制下联合LDPC 码的PNC 系统与QPSK-BPSK调制PNC 系统在目的节点的比特异或规则相同.

A 节点的比特异或规则为：

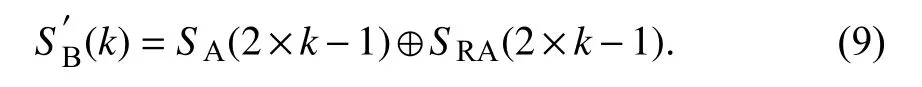
B 节点的比特异或规则为：

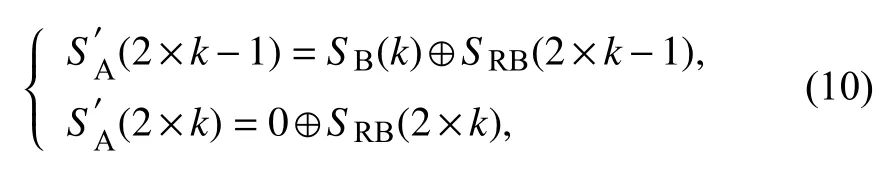
其中，k=1,2,3,···,K.

3 系统性能仿真分析

本节使用Matlab 开发平台进行仿真，实验假设系统两端交互的信息具有良好的同步性，传输信道为标准加性高斯白噪声信道，不考虑信号衰落等问题，仿真时节点A 总数据量为24 000 比特，信道编码采用码长为256，有效信息位长224 的LDPC码，LLR-BP 译码算法的最大迭代次数为40 次.

3.1 QPSK-BPSK 调制PNC 系统仿真 图6 为上行非对称信道下采用QPSK-BPSK 调制的PNC 系统的误比特率（Bit Error Rate，BER）性能. 在0～6 dB低信噪比区域内，系统BER 曲线的减小量不到10-1数量级，变化较为平缓；在6～12 dB 信噪比区域内，随着信道条件转好，系统的BER 值也从10-1数量级降到10-3，变化趋势明显. 虽然节点A、B 两端采用不同的调制方式，但A 到B 端、B 到A 端两条端到端的BER 性能曲线仅存在略微区别，整体变化趋势基本一致，因此在后续仿真中，只选取A到B 端的BER 性能进行比较.

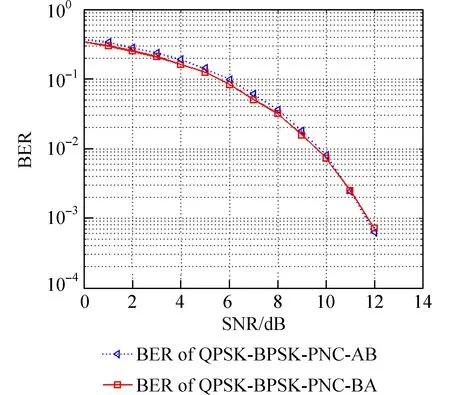
图6 QPSK-BPSK 调制PNC 系统BER 性能Fig. 6 The BER performance of QPSK-BPSK-PNC system

3.2 QPSK-BPSK 调制下PNC 系统和NC 系统仿真 图7 为基于QPSK-BPSK 调制的NC 系统和PNC 系统的BER 性能. 从曲线整体变化看，NC 系统的端到端误码率性能优于PNC 系统. 从信噪比与误码率性能之间的相互关系看，在0～6 dB 低信噪比区域内，NC 系统的BER 性能稍好于PNC 系统，在6 dB 以上的高信噪比区域，BER 性能曲线变化趋势明显，在BER 为10-3数量级时，QPSK-BPSK调制PNC 系统的性能比QPSK-BPSK 调制NC 系统的性能损失约1.8 dB.

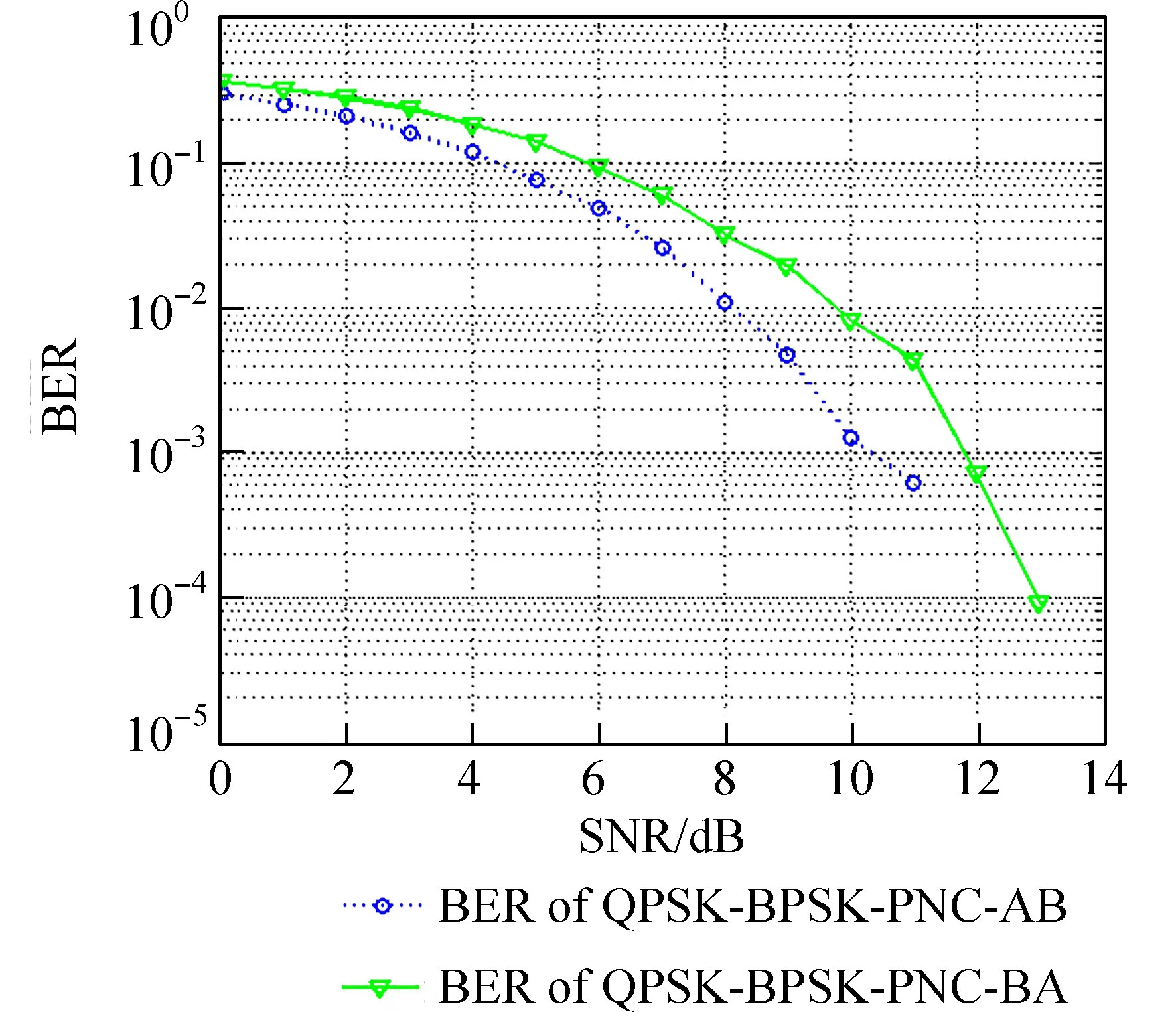
图7 QPSK-BPSK 调制PNC 系统、NC 系统BER 性能Fig. 7 The BER performance of QPSK-BPSK-PNC，QPSKBPSK-NC system

综上所述，NC 系统比PNC 系统的误码率性能较优，但是在双向中继信道中采用NC 技术完成一次信息交互需要3 个时隙，而采用PNC 技术只需要2 个时隙. 因此系统以一定的误码率性能为代价，采用PNC 技术的系统吞吐量能够提高50%.

3.3 BPSK 调制、QPSK-BPSK 调制、QPSK 调制下PNC 系统仿真 图8 为基于BPSK 调制、QPSK调制和QPSK-BPSK 调制的PNC 系统的BER 性能. 从曲线整体变化看，BPSK-PNC 系统端到端误码率性能较优，QPSK-BPSK 调制PNC 系统端到端误码率性能次之，QPSK-PNC 系统端到端误码率性能较差. 从信噪比与误码率性能之间的相互关系看，在0～4 dB 低信噪比区域内，3 个PNC 系统的BER 性能相差较小，在4 dB 以上的高信噪比区域，在BER 为10-3数量级时，QPSK-PNC 系统的性能比BPSK-PNC 系统和QPSK-BPSK 调制PNC 系统的性能分别损失约2.9、1 dB；在BER 为10-4数量级时，QPSK-PNC 系统的性能比BPSK-PNC 系统和QPSK-BPSK 调制PNC 系统的性能分别损失约5、3 dB.

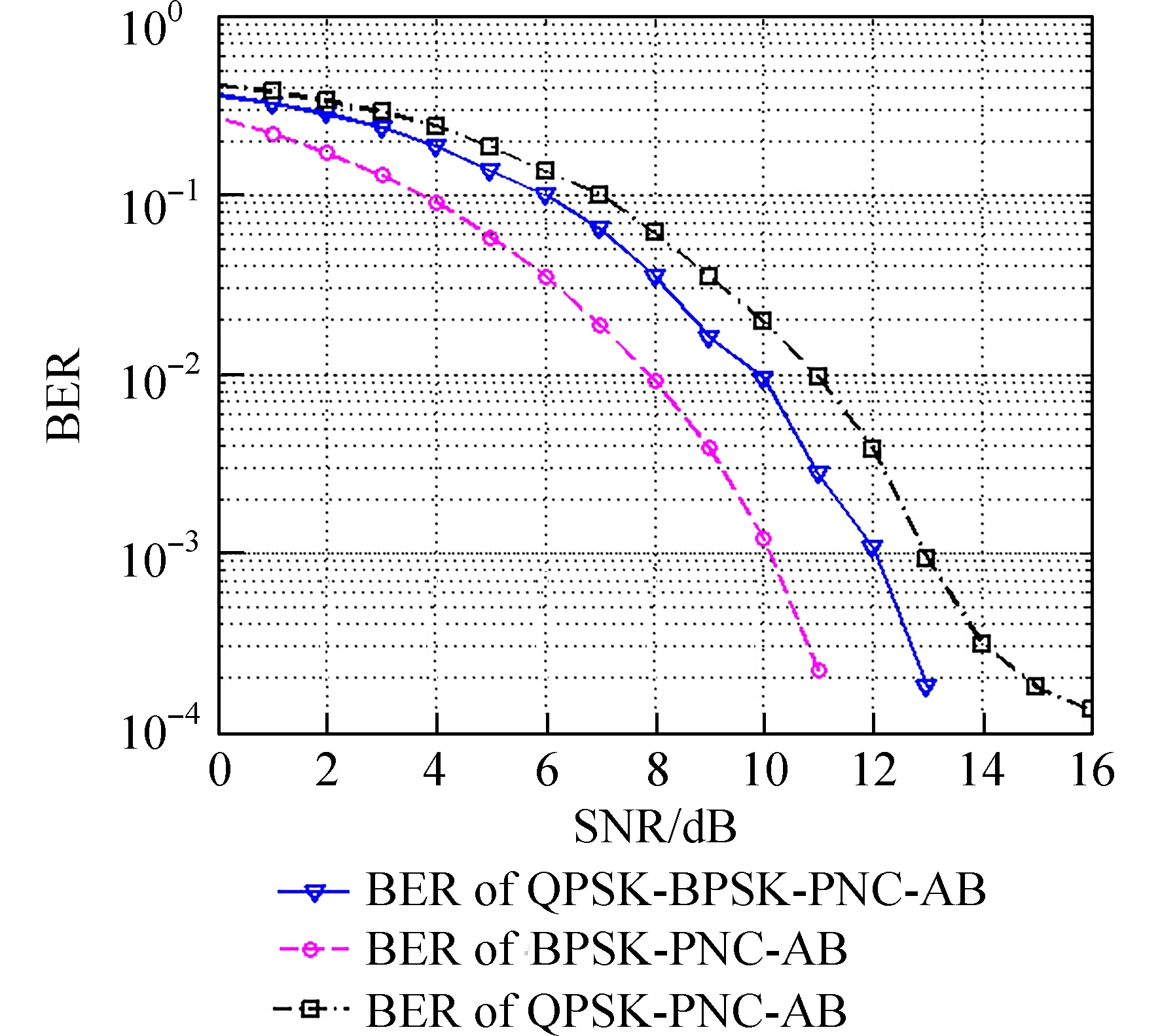
图8 BPSK 调制、QPSK-BPSK 调制与QPSK 调 制 下PNC 系统BER 性能Fig. 8 The BER performance of BPSK-PNC，QPSK-BPSKPNC and QPSK- PNC system

在图8 中，对3 种PNC 系统的传输性能进行对比可知，QPSK-PNC 系统一次信息交换可传输4个比特数据，其传输效率最高，BER 性能最差.BPSK-PNC 系统一次仅传输2 个比特，传输效率最差，BER 性能最好. 而QPSK-BPSK-PNC 系统一次可传输3 个比特，相比BPSK-PNC 系统而言，传输效率有50%的提升，BER 性能介于前两者之间. 当信噪比优于13 dB 时，QPSK-BPSK-PNC 系统的BER 性能，与QPSK-PNC 系统相比，有7.6%以上的改善.

3.4 不同功率分配比下QPSK-BPSK 调制PNC系统仿真 图9 为在不同功率分配方案下QPSKBPSK 调制的PNC 系统的BER 性能. 通过对图9中6 条BER 性能曲线的比较，当功率分配比值在1 附近时，BER 性能曲线相差较小. 当系统功率分配比为0.25、0.5、0.75、1、2、4 时，信噪比分别约在19.3、14.4、12.4、11.9、15.7、21.6 dB 时BER 性能达到10-3数量级. 通过对不同功率比下的PNC系统误码率性能对比，当系统功率分配比为1 时，系统的BER 性能最优.

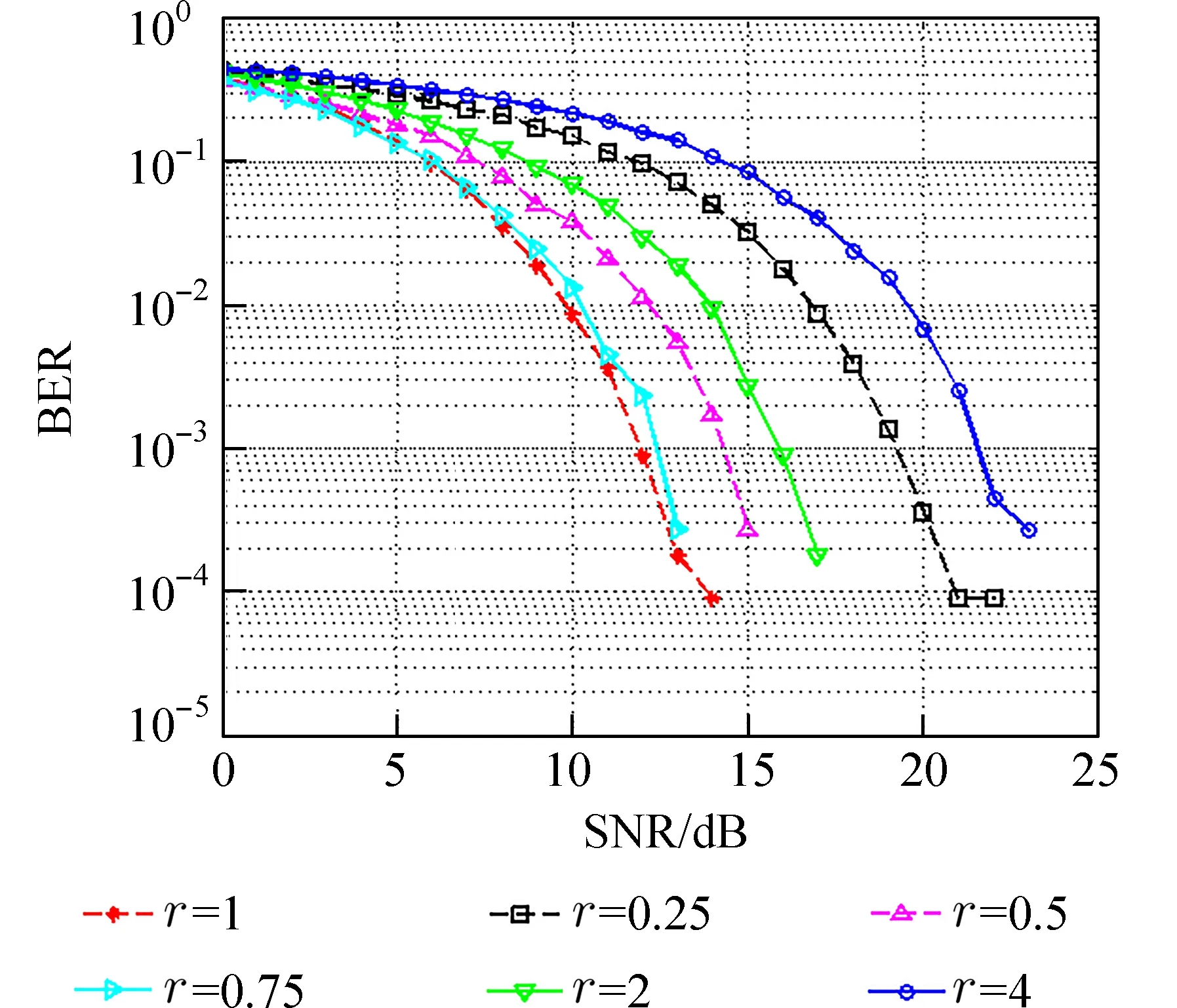
图9 不同功率分配比下的QPSK-BPSK 调制PNC 系统BER 性能Fig. 9 The BER performance of QPSK-BPSK-PNC system under different power allocation

3.5 QPSK-BPSK 调制下联合LDPC 码的PNC 系统仿真 图10 为QPSK-BPSK 调制PNC 系统与QPSK-BPSK 调制下联合LDPC 码的PNC 系统BER性能. 在0～10 dB 低信噪比区域内，此时信道条件较差，加入信道编码前后的两个PNC 系统BER 性能曲线变化趋势较为缓慢且极其接近，通过调整LDPC 码的参数也不能很好地改善系统的BER 性能. 当信噪比大于10 dB 时，此时信道条件较优，BER 性能随着信噪比的增大呈现出联合LDPC 码的PNC 系统BER 性能较优的趋势. QPSK-BPSK调制PNC 系统与QPSK-BPSK 调制下联合LDPC码的PNC 系统分别约在11.2、12 dB 时，BER 性能达到10-3数量级，联合LDPC 码的PNC 系统比PNC系统的BER 性能提升约0.8 dB.

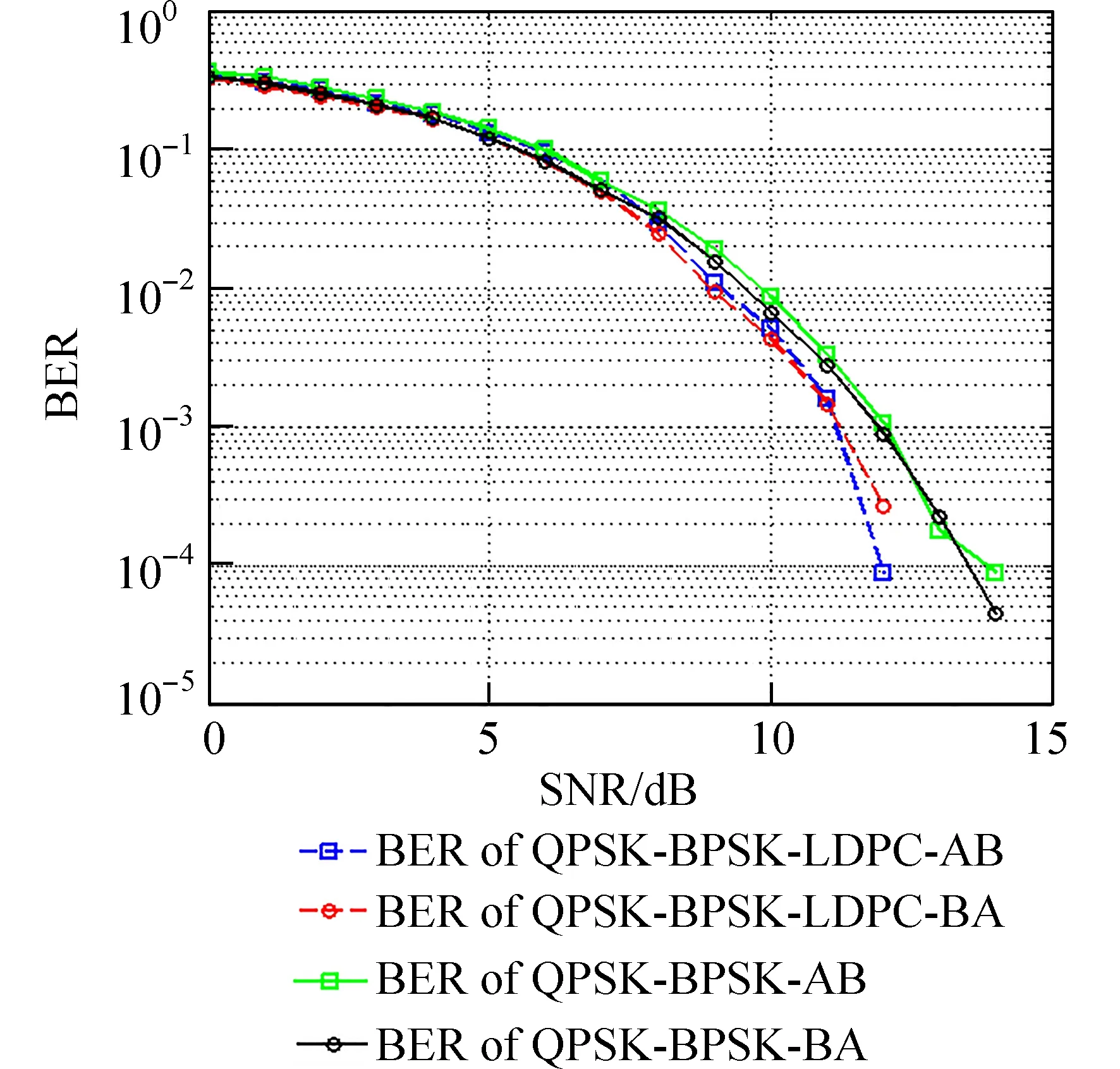
图10 加入LDPC 码前后PNC 系统BER 性能Fig. 10 The BER performance of PNC system before and after joint LDPC code

根据上述分析，PNC 技术会导致一定的性能损失，但是可以通过采用信道编码技术来改善系统的BER 性能，减小性能损失. 因此QPSK-BPSK 调制下联合LDPC 码的PNC 系统在保证吞吐率性能的同时，能够进一步改善系统的BER 性能.

4 结语

在物理层网络编码系统中，针对上行非对称信道，在源节点两端采取QPSK-BPSK 调制，中继节点制定解调映射算法，并在目的节点设计比特异或规则，解决了终端进行异或时位数不相等的问题，从而实现系统两端的信息交互过程. 相较于传统对称调制方案，在保证系统传输效率的前提下，采用QPSK-BPSK 调制的PNC 系统能够改善系统的信息传输性能. 而在功率优化分配方案下加入LDPC编码，能够进一步改善系统的误码率性能.

本文仅以上行非对称信道条件展开分析，而在实际通信过程中信道条件是复杂多变的. 因此，接下来的研究将采用更高效的调制技术和功率分配策略，以应对复杂多变的信道条件，进一步提升系统传输的有效性与可靠性.