重尾条件下现代保险风险模型的破产概率模拟计算及分析

郭红财

(安徽扬子职业技术学院 基础数学部，安徽 芜湖 241080)

一、引言

随着人民生活水平不断提高及社会保障体制的逐步完善，现代保险业成为日常生活中不可缺少的一部分[1]。保险精算对于现代保险企业来说是核心技术，保险精算学主要应用统计模拟与计算、概率论、现代数学分析、风险理论、极值理论、金融和保险学理论及方法，在经营管理中，对保险公司各环节做出准确测算、数量分析，从而为保险公司经营管理、战略抉择提供依据[2-4]。风险理论在保险精算学中属于最关键部分之一，它是保险人实行责任储备金的科学合理计提、保险公司产品差异化科学合理计价、偿债能力的有效管理、再保险资金合理配置、保险公司风险管理、企业破产准确预警等重要理论基石，是保险公司工作人员对其企业保险业务开展风险管理的重要理论依据和有高效运营理论基础保证[5]。对保险公司而言，最大风险是偿付能力的缺乏[6]。在保险公司偿付能力风险预测中，破产理论属于重要理论，其是风险理论核心部分，运用随机过程，应用概率论、极值理论等工具，基于一系列合乎现实情况假设，通过模型的构建进行推导、分析，最终获得保险公司收益的过程，并进行保险公司破产前盈余及破产概率的计算等[7]。破产学说从理赔视角展开风险因素对保险人偿债能力影响的研究，偿债能力属于一项受各种风险和不确定性原因直接影响的变量，而偿债能力在经营风险理论研究中则被视为一种随机过程。就保险公司来说，当其需偿还的投资亏损，索赔额超过其初始准备金，投资收益，保费收入后，则有净损失为正值出现时，保险公司则面临破产。破产概率是评估保险公司经营状况的重要指标。

风险是造成个人身体伤害、社会责任等风险事件产生，损失的可能性。风险通常采用概率作为可能性测度进行量化。个别的风险事件产生具有偶然性，当通过观察大量的风险事件后发现，风险会有规律地出现，并利用统计分析方法进行对大量且相互独立的偶发风险事件的处理时，其结论可将风险规律较精确地表现出来，而通过以往资料，再结合数理统计方法、概率论等，可将风险事件的损失幅度和出现机率等估计出来，并实现了损失分布，模型的建立[8]。保险是为了转移分散风险，得到风险损失必要补偿而产生的。保险问题属于非常重要的现实理论问题，保险风险理论主要是利用随机过程理论、概率论进行数学模型的构建，由此可实现对各类经营风险行业业务的定义，并着重对资产盈余等有关指标进行概率统计，如对破产概率等加以分析研究，由此可为保险公司长期稳健运营提供理论支持。经营风险理论是对决策部门实行危险性预测，定性研究的基本理论，在这一基础理论中，风险经营稳定性分析方法占据了主要地位，通过破产理论开展经营风险的稳定性分析，许多学者构建数学模型解决此类问题[9]。破产概率在风险理论中属于热点的课题。有限时间破产及最低偿付能力概率的重尾部分存在直接联系，其本质与破产概率分布分位数相当。在理论和实践上，研究重尾风险模型破产概率均有重要意义，特别是在模型中要对保险风险对偿付能力，保险公司金融风险的影响同时考虑。因而，文章在重尾条件下，对现代保险风险模型的破产概率进行模拟计算及分析。

二、经典风险模型

其中，保费收入率是单位时间内的收入，用c表示；初始准备金用u表示，ct为保险公司到t时刻为止收入的总保费；第k次索赔到达时间为{Tk,k>0}，00}，{Xk,k>0}独立同分布；到时间t为止的索赔次数为{Nt,t>0}；索赔时间间隔为{Yk,k>0}，Yk=Tk-Tk-1,k=1,2,…。

近年来，一些学者改进完善经典风险模型，其中在索赔额{Xk,k>0}属于小额索赔时，服从指数分布的随机变量序列。但实际上造成保险公司破产通常是非常严重的大额索赔，在极短时间内，巨灾风险事件强烈冲击保险市场和保险业，并引发连锁理赔反应，进而使保险企业破产潮进一步加剧。美国在1969年到1998年因巨灾损失约造成6%的保险公司破产。因而，巨灾大额索赔越发成为学者关注的焦点。这种现象实质上在风险理论中较为普遍，被称为“二八现象”，即在十次理赔中，有两次大额理赔索赔额的总和占索赔总额的80%。在1997年，Embrechts等将索赔额分布推广到重尾分布上，重尾分布是指矩母函数不存在的分布[10]。

引理1：

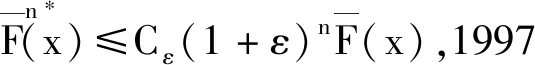
引理2：

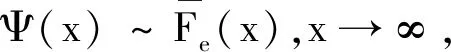
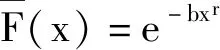
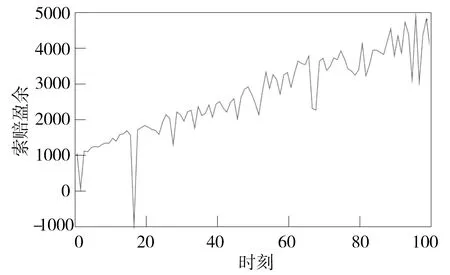
图1 剩余过程的示例路径

三、具有潜在索赔风险模型的破产概率及数值

在进行模拟时，将分布族扩大到比L∩D族更大的S族，索赔额序列{Bk:k=1,2,……}为独立同分布(i.i.d)的随机变量序列，从而获得破产概率渐近表达式，并采用MATLAB进行该结果的数值模拟。

在进行模型的破产概率的渐近表达式的研究时，需要进行如下的假设：

定理2：

(2)

表1 破产概率理论值与模拟值的比较

由表1得知，理论值、模拟值随着初始资金x的增大渐渐接近，这说明定理2合理。选取T=205，对以上步骤进行重复，从而得到表2所示的T=205时的模拟结果。

表2 T=205时的模拟结果

由表2得知，模拟值和理论值存在一定差别，这可能和实验参数、次数选取有关。

四、上尾独立情形下潜在索赔风险模型的有限

在很多实际案例中，风险间不是相互独立，因此，研究索赔额不独立风险具有一定的实际意义。在概率极限理论中，随机变量的不独立性长期受到概率统计学家的关注，对随机变量的应用和性质的讨论从未间断[11]，有学者得到相依随机变量两个极限定理[12]。Chen对更新风险模型负相依重尾索赔破产概率进行研究[13]。本研究讨论的是潜在索赔额是上尾独立L∩D族随机变量序列时，潜在索赔额风险模型有限时间的破产概率。上尾独立相依性结构是对随机变量右尾间的负相依(ND)、相依性、负相伴(NA)是上尾独立的特殊情形的描述。相比检验整个序列随机变量间相依性，检验上尾独立检验随机变量两两间相依性更容易，关于索赔额的破产概率渐近等价公式上尾独立性不敏感。

(一)上尾独立的定义及相关性质定理

设定一个边际分布为F、G的联合分布函数为H，则有一个Copula函数C存在，对全部的x,y∈R，均存在H(X,Y)=C(F(x),G(y))。两个随机变量X、Y的边际分布为F(x)、G(y)，由一个二元Copula函数C确定X、Y间相依性构。

定义1(上尾相依)

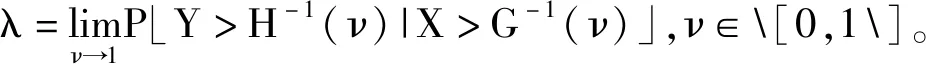
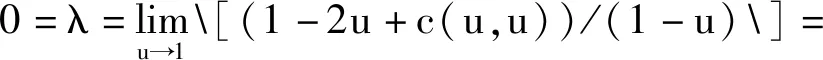
其中，极值出现小概率事件通过上尾独立结构来描述，当极值无穷大时，第二个极值的概率接近零；当X、Y表示索赔随机变量时，上尾独立性表示已知一个保单索赔为最大时，另一个保单索赔为最大的概率趋于零；在{Xk,k=1,2,……}同分布时，如果ND相依，则上尾独立。

(二)上尾独立情形下潜在索赔风险模型的破产概率

引理3:

如果随机变量序列{Xk:k≥1}为上尾独立，则{IkXk:k≥1}为上尾独立。证明：对任意的k≥0，则存在如下关系：

从而可知，{IkXk:k≥1}为上尾独立。通过L、D族定义可知，{IkBk:k≥1}的分布属于L∩D，且存在{IkXk-(1+ρ)μ:k≥1}分布属于L∩D。

引理4：

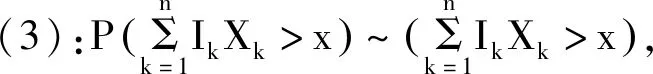
在n≥2时，

通过引理4可获得

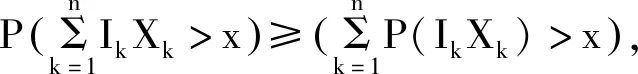
对A1进行处理，乘积IkXk∈L，因此，

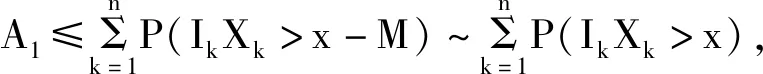
结合引理4和D族的定义可获得如下关系：

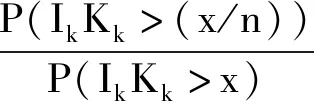
五、结论

巨灾等类极端事件一旦发生势必会给保险业务来带重大风险，导致保险公司面临财务危机，严重时会造成其破产。文章在重尾条件下，运用数理统计、概率论基础知识，对现代保险风险模型的破产概率进行模拟计算及分析，得出如下结论。

第一，在不同分布族上，通过分析潜在的索赔风险模型破产概率，从而得出破产概率的渐近表示。在重尾分布条件，通过进行对潜在理赔风险模型破产概率及数值模拟，在对潜在理赔额排序满足S族假定下，得出了有限时间的破产概率渐近表达式，得出理论值、模拟值比较接近，模拟结果合理。

第二，在上尾独立性情况下，分析潜在的理赔风险模型受限时期破产概率，若假定与上尾独立性相同分布的重尾随机变量顺序为理赔总额顺序，则潜在的理赔总额顺序将服从于L∩D族，从而得到有限时间破产概率的渐近表达式。

第三，在今后研究中，应改变索赔额间的关系，在数值模拟中将索赔额序列间关系由独立推广到各种相依，联系实际情况。在进行重尾检验时，将理论和实际通过联系实际数据联系起来，力求做到数学服务于生活。