可见，让计算思维真正落地

徐钢强

摘要：本文以程序设计教学为研究阵地，针对程序设计教学中从数学思维到计算思维、现实问题与计算机结构化问题之间的“断桥”现象，从问题界定、对象抽象、子问题分解、模式识别和建模自动化实现等方面，将计算思维过程可视化，将头脑中模糊的、随性的思维碎片，变成可见的、清晰的、系统的思维流程，让学生通过可视化分析，亲历计算思维的整个过程，从而透析计算思维的内在实质，让计算思维培养落到实处。

关键词：计算思维;程序设计;可视化

中图分类号：G434  文献标识码：A  论文编号：1674-2117（2022）06-0000-04

作为信息技术学科核心素养的重要组成部分，计算思维让信息技术学科的思维培养有了明确的指向，广大一线教师也在教学中纷纷渗透计算思维培养的意识。但不可否认，更多的计算思维培养还停留在教师理念和教学设计层面，真正让学生亲身演绎计算思维的过程还较缺乏。针对这种现状，笔者从程序设计教学领域出发，尝试通过将计算思维过程可视化，让学生在可视化分析中去感受、演绎计算思维的过程，从而透析计算思维的内在实质，在潜移默化中实现计算思维的培养。

● 程序设计教学中的思维“断桥”现象

1.现实问题与计算机结构化问题之间的“断桥”

信息技术之所以能够应用于现实，推动人类社会发展，是因为它能够对现实问题进行计算机化的处理，也就是让现实中的问题变得可计算。而这就需要对现实问题进行结构化分析，并抽象和建模。对学生而言，由于固有思维的影响，对现实问题描述的结构化分析和抽象建模是他们所面临的一个短板。

2.从数学思维到计算思维之间的“断桥”

计算机处理的很多问题其实都是数学问题，尤其是对于程序设计初学者而言，由于其数学思维的先入为主，因此看待问题很容易从数学层面去分析，用数学方法去解决，这就使得他们的思维停留在数学思维层面，而无法跨越到计算思维层面。例如，同样是计算1+2+3+…+100的和，学生自然而然地会想到应用等差数列的方式求解，而且确实能够直接通过公式利用计算机进行解决，并且从效率上来讲，确实优于计算机利用循环累加的方式进行求和，但是这样就限制了学生利用计算思维方式去看待问题，对于培养他们的计算思维，是存在一定缺陷的。

以上“断桥”现象，归根结底就是计算思维培养离真正落地还有距离。

● 从编程工具可视化到计算思维可视化

1.编程工具的可视化

作为编程语言，从纯代码的Basic、Pascal、C语言等，到基于所见即所得的Visual Basic、Visual C++，乃至积木式、图形化的，编程工具的可视化极大地简化了程序代码的编写难度，对程序设计的普及有着极大的促进作用，但从某种程度上来讲，这只是一种形式上的简化，并非思维层面的实质提升。

2.计算思维的可视化

计算思维的可视化并非只是简单地呈现出来，其实质是让学生从计算思维的视角去分析、解决问题。因为程序设计要求的思维程度较高，而初学者对问题进行分解抽象、再加工的能力有限，所以容易造成无从下手的局面，而让头脑中的思维过程通过某种形式表现出来，演绎整个思维过程，能让初学者对对象、子问题、规律等有效把握，进而完成抽象加工和数学建模。

● 计算思维可视化在程序设计教学中的探索

1.问题界定可视化

程序设计就是在计算思维下解决某个实际问题的过程，但现实中的问题往往缺乏一定的结构性，而且在描述上会有很多其他干扰性因素，也可能会有一些隐含因素，导致学生对问题看不懂、看不全，其实质就是问题界定环节缺失。教师可通过对问题的结构化分析，明确需要解决什么、隐含条件或限制条件是什么，这对学生准确把握要解决的问题的实质非常重要。

例如，有问题描述如下：双休日，陶陶打算帮爸爸做点事。爸爸对陶陶说：“仓库中有一批长短不一的钢管，需要切割成等长的小管，本着节约的原则不能有零头浪费，同时因为切割也很麻烦，要让切割的次数尽量少一些，你能不能帮我计算一下每根多长最合适。”陶陶犯难了，你能通过编程帮他解决这个问题吗？

该问题通过情境化的描述，将问题的条件隐含在描述中，这就需要学生根据描述对问题进行界定，教师可引导学生进行结构化分析（如表1）。

通过问题界定的可视化，将问题的需求一一罗列，同时对每个需求进行相应分析，形成分析表，最后得出分析结论，这样一方面有助于促进学生对问题描述的把握，另一方面也为学生分析思维过程提供了支架，降低了难度。

2.对象抽象可视化

利用计算机解决实际问题，从某种程度上来讲，就是为了解决“谁做什么”的问题，这里的“谁”指的就是计算思维中的对象，“做什么”就是算法。从现实问题中的“谁”到程序设计中的数据结构，需要对对象进行抽象，而这个抽象过程，就是对对象进行结构化加工。对于程序设计的初学者而言，如何建立起具体事物到数据结构对象之间的抽象至关重要，这是利用计算思維解决实际问题的关键。

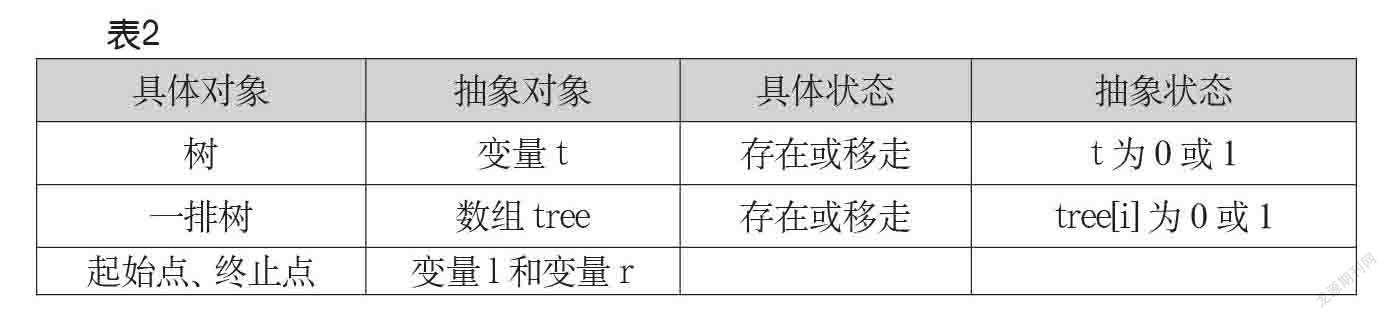
例如，问题“校门外的树”，描述如下：某校大门外，长度为L的马路上有一排树，每两棵相邻的树之间的间隔都是1米。由于马路上有一些区域要用来建地铁，这些区域在数轴上用起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数，区域之间可能有重合的部分。现在要把这些区域中的树（包括区域端点处的两棵树）移走，你的任务是计算“将这些树都移走后，马路上还有多少棵树”。

在表2中，通过将具体对象和抽象对象、具体状态和抽象状态结合分析，在可视化状态下呈现出来，很容易完成从具体到抽象的过渡，从而建立起问题的数据结构，为后面的算法设计打下基础。

3.规律抽象可视化

规律永远是程序设计的重要内涵，而规律的背后，就是利用计算思维对现实问题的可计算加工，也就是发现“自动化”点，这个过程往往是最有难度的。规律抽象可视化通过两个步骤来实现：一是发现规律;二是规律的抽象提炼，进而完成数学建模，实现计算思维的自动化表达。

例如，数组数据转置问题，即将原数组n个单元首尾倒置存放。可视化过程如下图所示。通过图中的规律抽象可视化分析，其思维过程从具体到抽象完整地体现了出来，算法的设计就是临门一脚的事情了。

4.模式识别可视化

当问题具有相同的特征时，它们的解决会变得更简单，因为当存在共同模式时，可以用相同的方法解决此类问题，这就是模式识别。

当面对一个程序问题时，引导学生通过对问题的分析、分解，识别哪些特征是熟悉的，可以用什么数据结构来表示;哪些过程似曾相识，可以用之前学过的哪些方法来解决;哪些问题是目前尚无已有经验可以解决的，它们就是学习新知或进行探索的重点。通过模式识别分析，一方面有助于学生敏锐地发现问题中的抽象特征，学会对已有经验进行迁移应用，另一方面也有助于学生发现未知领域，触发探究动力。

例如，求n个数在数轴上的最大间隙问题，其模式分析如表3所示。

5.优化处理可视化

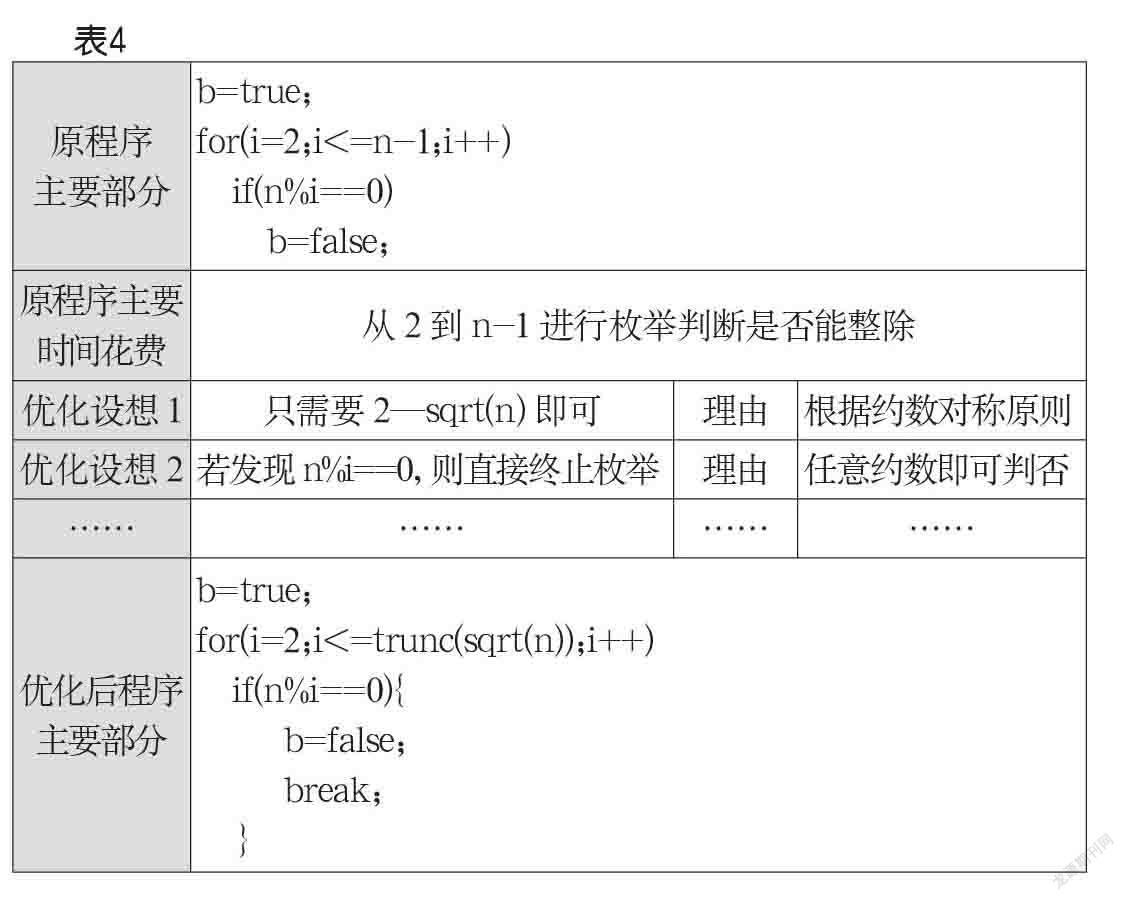
优化处理实质上是对现有程序的迭代和再加工，是建立在对现有算法充分分析的基础上进行的，是对原有算法的全面反刍。可优化就意味着现有算法存在着一定的冗余，发现冗余并提出相应的改进，是算法思维的进阶和迭代。同时，这也对编程者提出了更高的要求，优化处理的可视化分析就是帮助编程者对原有算法进行全面复盘，进而发现可优化点。例如，素数判断算法，如表4所示。

表4中的原始算法是根据素数定义进行模拟得到的。通过对比分析，提出优化设想，从而实现对原程序的优化，使得整个思维的反刍和迭代过程可视化，让思维的每一次进阶和迭代都有借力的支点。

总之，从问题界定、对象抽象，到子问题分解、模式识别，进而优化迭代，其思维过程的可视化就是让学生真正融入到思维的演绎中去，让学生成为思维过程的主宰者，而不是仅仅停留在师生交互的一问一答中。只有让学生沉浸在计算思维的浪潮中，才能使其真正发现计算思维的深邃魅力，让整个过程充满挑战与乐趣。

参考文献：

[1]王荣良.基于思维视角的计算思维教育落实[J].中小学数字化教学，2020（01）：20-23.

[2]费海明.计算归简，分合衍变——计算思维内涵探析与教学创意[J].中国信息技术教育，2020（20）：85-88.