电-热综合能源系统概率潮流计算
2022-03-23廖星星李华昌
廖星星,李华昌
(中国电建集团江西省电力设计院有限公司能源规划研究中心,江西 南昌 330096)
0 引言
为解决煤炭、石油等化石能源的紧缺问题,综合能源系统应运而生[1]。近年来,随着热电联产机组的逐步应用,电-热综合能源系统得到了快速发展[2]。并且,随着风电等新能源的大规模接入,电-热综合能源系统面临着大量的不确定性,这给系统安全稳定运行带来了巨大挑战。为解决该问题,相关学者引入了概率潮流(Prababilistic Power Flow,PPF)的计算方法。
PPF 计算思想由国外学者于1974 年首次提出[3],发展至今,其计算方法主要有:模拟法、近似法、解析法。其中,模拟法中主要有蒙特卡罗模拟(Monte Carlo Simulation,MCS)等相应改进算法[4]。近似法主要包括两点估计法和三点估计法[5]。解析法主要代表为半不变量法(Cumulant Method,CM),因其计算效率较高而得到了广泛应用[6-7]。
目前,在综合能源系统的概率潮流研究中,文献[8]首次采用MCS 对电-气互联综合能源系统概率能量流进行分析。文献[9]采用聚类和多段线性化的方法提高计算效率和精确度,但其本质上仍为模拟法。此外,也有部分学者采用拉丁超立方采样法对综合能源系统概率潮流进行求解,在保证精度的同时也提高了计算效率[10]。文献[11]基于最大熵原理对电-气互联综合能源系统概率潮流进行计算。而在上述概率潮流计算中其对象多集中于电-气综合能源系统或所提算法计算效率较低,因此需提出一种精度高、速度快的电-热综合能源系统概率潮流计算。
基于上述分析,文中提出了一种基于半不变量法的电-热综合能源系统概率潮流计算方法。首先,采用截断通用分布模型和有界正态分布分别拟合风电出力和负荷的随机波动。其次,针对电-热综合能源系统中的随机性问题,提出半不变量法对其概率潮流进行求解。最后,采用不同概率拟合方法进行概率分布函数拟合。在此基础上,以巴厘岛电-热综合能源系统进行测试分析,验证了所提方法在该领域概率潮流计算中的有效性和快速性。
1 电-热综合能源系统模型
电-热综合能源系统主要由3 部分组成:热力系统水力模型、热力系统热平衡模型、电力系统潮流模型。其中,每个组成部分之间通过相应的电-热耦合元件进行连接[10]。
1.1 热力系统水力模型
热力系统水力模型包含以下方程:

式中:A为网络关联矩阵;m为热网管道流量;mq为节点流入负荷流量;B为回路关联矩阵;hf为管道压降;K为管道阻力系数。
1.2 热力系统热平衡模型
热平衡模型主要方程如下:
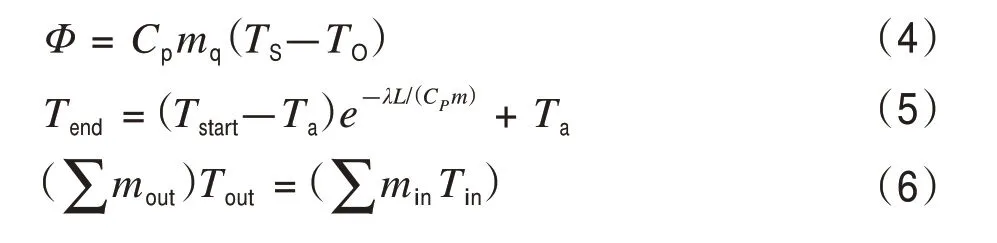
式中:Φ为热负荷;TS和TO分别为供水温度和回水温度;Cp为水的比热容;Tend和Tstart分别为管道首端温度和末端温度;Ta为环境温度;L为管道长度;λ为传热系数;mout和min分别为流出和流入节点的管道流量;Tin和Tout分别为输入管道末端的温度和节点混合温度。
1.3 电力系统潮流模型
电力系统潮流模型可表示为:
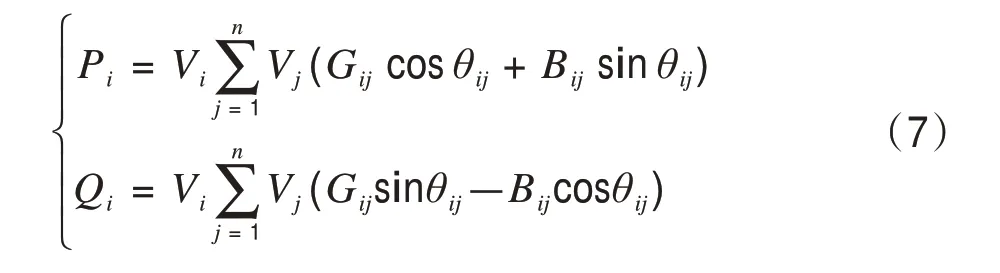
式中:Vi和Vj分别为节点i和j的电压幅值;Gij和Bij分别为节点导纳矩阵中的电导和电纳;θij为节点i和j的相角差。
1.4 电-热综合能源系统稳态潮流
热平衡模型主要包含以下方程:采用牛顿拉夫逊法进行联合迭代求解式(1)至式(7)可得到稳态潮流,其修正方程表示如下:

式中:ΔP和ΔQ分别为电力系统有功和无功修正量;ΔΦ和ΔT分别为热负荷修正量和节点温度修正量;J为雅克比矩阵;Δθ和ΔV分别为相角修正量和节点电压幅值修正量;Δm为管道流量修正量。
2 风电出力和负荷不确定性模型
电-热综合能源系统中接入风电导致其随机性加剧。同时,系统电、热负荷本身也存在一定的波动性。因此,文中主要考虑风电出力、电负荷和热负荷的不确定性。
2.1 负荷的有边界正态分布模型
电、热负荷不确定性通常可用正态分布函数描述,但由于实际负荷存在最小值和最大值,因此文中采用有边界的正态分布函数对其不确定性进行建模,表示如式(9)、式(10)[12]:
式中:Pmin和Pmax分别为电负荷的最小和最大值;μP和σP分别为电负荷的期望和标准差;Φmin和Φmax分别为热负荷的最小和最大值;μΦ和σΦ分别为热负荷的期望和标准差。
2.2 风电出力的截断通用分布模型
相比采用正态分布、威布尔分布函数拟合新能源出力,截断通用分布模型可以更加灵活地拟合各种出力曲线,且存在有界定义域,与标幺化后的风电出力区间保持一致。基于上述优点,文中采用截断通用分布模型拟合风电出力[13],其概率密度函数f(x)具体表达如式(11)、式(12):
式中:α、β、γ分别为垂直参数、偏度参数和水平参数;M为标准化系数;x和x分别为风电出力区间上限和下限。
3 基于半不变量法的电-热综合能源系统概率潮流分析
针对电-热综合能源系统中的随机性性问题,提出半不变量法对其概率潮流进行求解,并在得到输出变量各阶半不变量后,采用不同概率拟合方法对其概率密度函数进行拟合。
3.1 电-热综合能源系统半不变量法计算模型
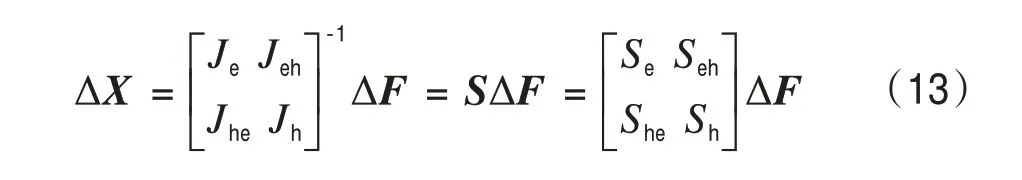
将式(8)进行变换后,即可得到基于灵敏度矩阵的电-热互联综合能源系统潮流计算修正方程式(13)。式中:S为灵敏度矩阵;Se、Seh、She、Sh、为各子阵对应的灵敏度矩阵;ΔX表示输出变量即电压、管道流量等存在的误差;ΔF表示输入变量即电热负荷、风电出力等。
基于式(13)则可建立起电-热互联综合能源系统半不变量概率潮流求解模型,对系统变量的概率特性进行求解,其计算方程如式(14)所示:
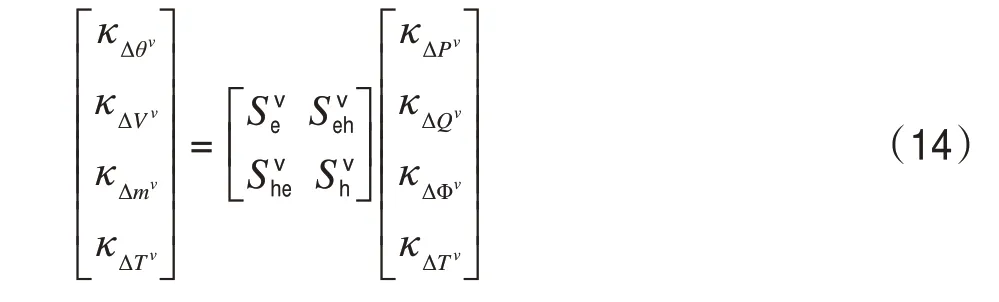
式中:κΔθv、κΔVv为相角和电压的v阶半不变量;κΔPv、κΔQv表示有功和无功的v阶半不变量;κΔmv表示管道流量的ν 阶半不变量;κΔTv表示温度的v阶半不变量;κΔΦv表示热负荷的v阶半不变量。
将所求变量写成标准化的格式:

式中:X0表示输出变量的基值,ΔX表示其所存在的误差。
由半不变量的性质并结合式(15),可将其写成如下形式:
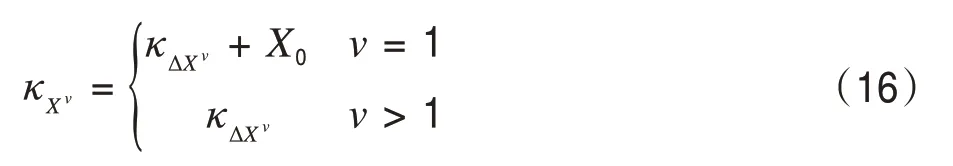
式中:κXv表示变量X的v阶半不变量;κΔXv表示ΔX的v阶半不变量。
为方便进一步对系统变量进行准确分析,可通过相应的级数拟合方法求得其概率密度函数。
3.2 概率分布函数拟合方法
采用半不变量法得到输出变量的各阶半不变量后,为方便进一步分析,通常需要对其概率密度函数进行拟合。下面介绍三种不同的函数拟合方法。
3.2.1 Cornish-Fisher级数展开
假设随机变量x的均值和标准差分别为μ和σ,将其标准化,即令δ=(x-μ)/σ,则采用Cornish-Fisher级数展开的概率密度函数为:
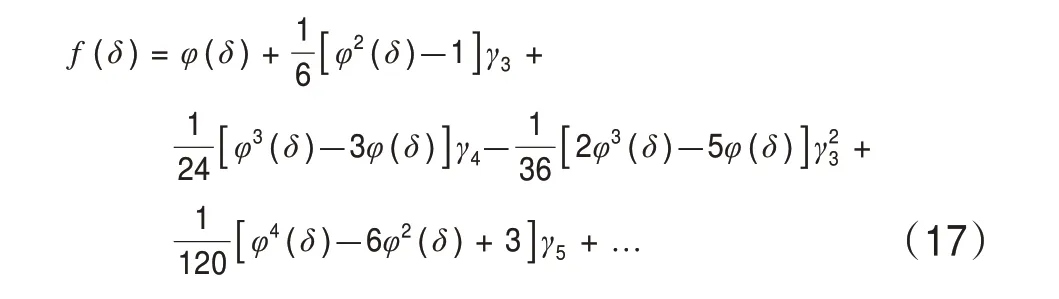
式中:f(δ)为标准化后的随机变量概率密度函数;φ(δ)为δ的概率密度函数;γi(i= 1,2,3,…)为各阶半不变量。
3.2.2 Gram-Charlier级数展开
Gram-Charlier级数展开又称正交展开式,其展开式为[5]:
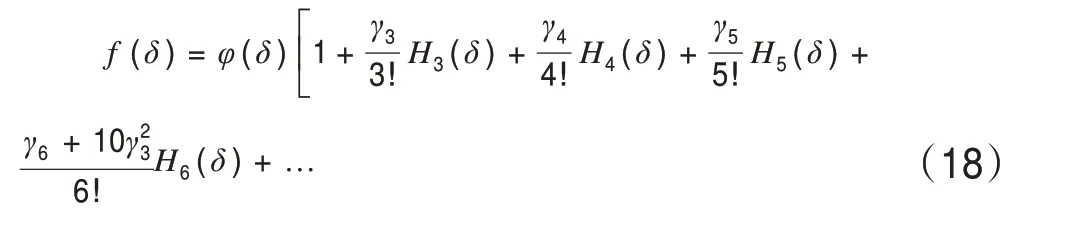
式中:Hi(δ)为Hermite多项式。
3.2.3 最大熵法
最大熵算法可以在已知随机变量各阶矩的情况下得到最优拟合概率密度函数,其数学模型可以表示为:
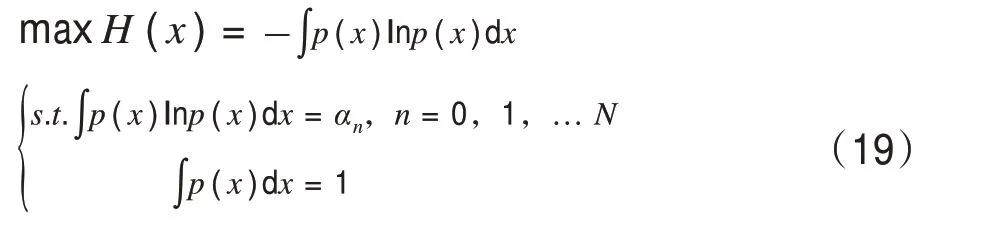
式中:H(x)为信息熵;p(x)为变量的概率密度函数;φn(x)=xn(n=0,1,…,N);αn为变量的n阶原点矩,其可与半不变量进行相互转换。
3.3 计算流程
综上所述,考虑电-热综合能源系统中所接风电及电、热负荷的不确定性,基于广义半不变量法对其概率潮流进行计算,其具体计算流程如图1所示。
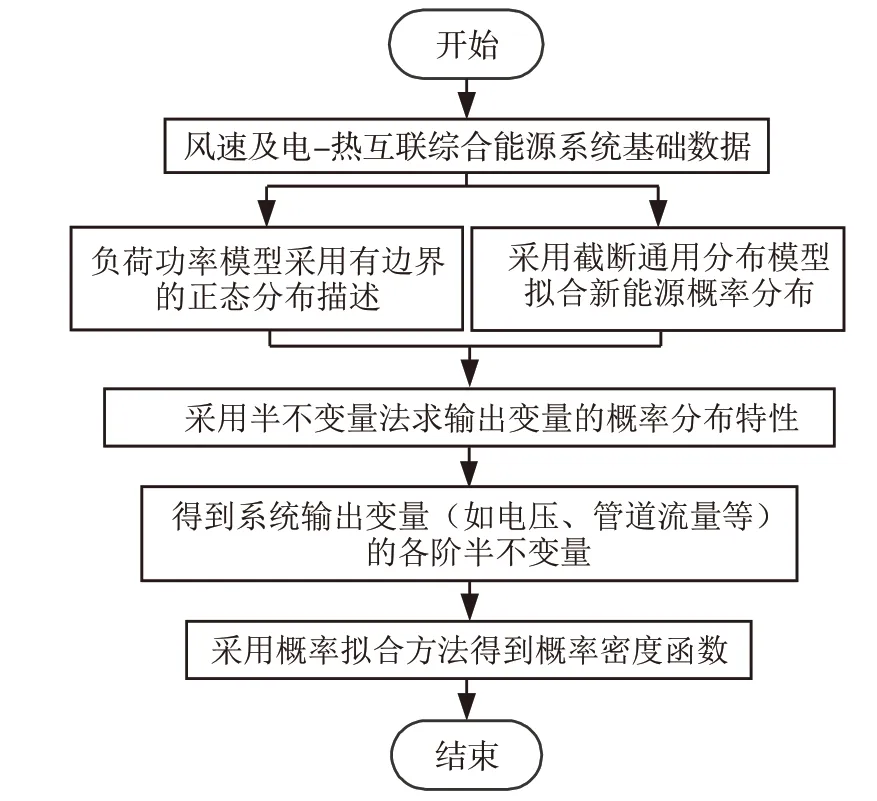
图1 概率潮流计算流程图
4 算例分析
为验证所提方法的有效性,采用巴厘岛电-热综合能源系统[10]进行测试分析,测试仿真平台为MATLAB R2014b。
为保证所提方法计算精度的准确性,将50000次蒙特卡洛模拟法潮流计算结果作为基准值,以相对误差指标表征输出变量统计数字特征的精度,以方差和的根均值(Average Root Mean Square,ARMS)指标表征概率分布的精度。
1)期望值和标准差的相对误差值:

2)输出变量的方差和的根均值指标:
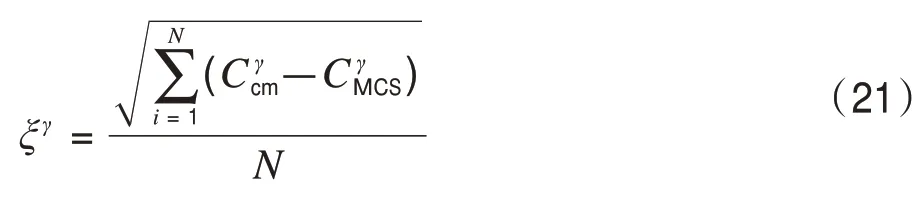
式中:ξγ为ARMS指标;和分别为采用和MCS所得概率密度曲线上第i点的值;N为取点个数。
4.1 巴厘岛电-热综合能源系统测试分析
巴厘岛电-热综合能源系统拓扑图如图2 所示,具体网络参数详见参考文献[10]。电网和热网之间通过CHP和P2H(电锅炉)进行耦合,其类型如表1所示。在电网节点4 和6 均接入额定功率为0.5 MW 的风力发电机,其相关系数设为0.5,风电出力的概率分布参数如表2所示。负荷期望值取为预测值,标准差取为期望的10%,相关性系数取为0.4[10]。
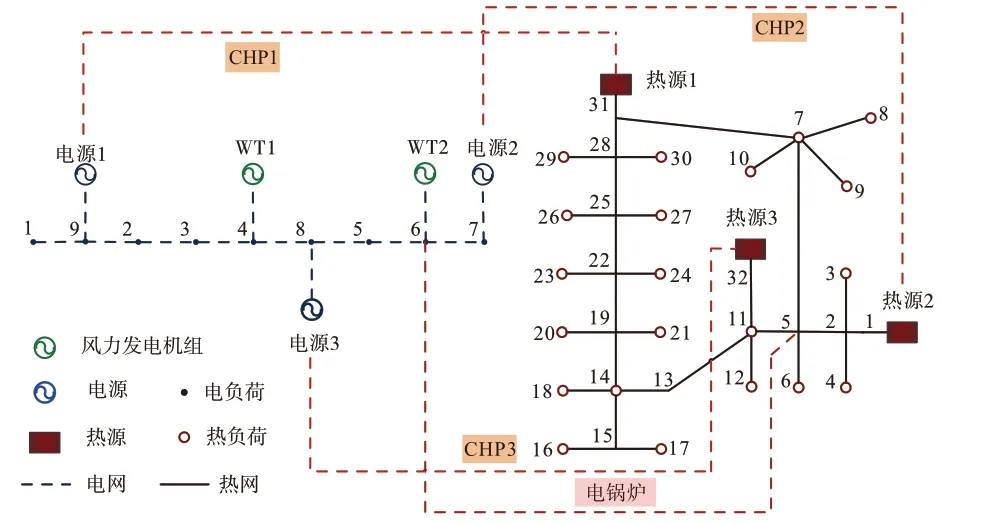
图2 巴厘岛电-热综合能源系统图

表1 CHP机组类型

表2 风电出力概率分布参数
将采用半不变量法的概率潮流计算结果与蒙特卡洛模拟法所得结果进行对比,从而进一步验证所提方法的有效性。表3 中εμ.mean和εμ.max分别为期望的平均相对误差和最大相对误差,εσ.mean和εσ.max分别为标准差的平均相对误差和最大相对误差。由表3 分析可得,期望最大误差为0.746%,标准差最大误差为3.746%,因此,从结果分析可得所提方法在数字特征精度的准确性。
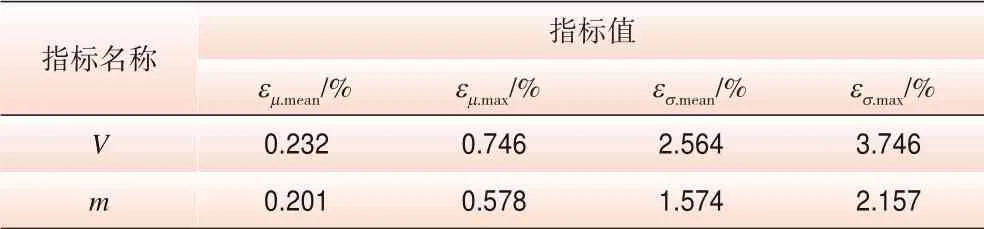
表3 电压、流量相对误差指标
表4中ξmean、ξmax分别为ARMS指标的平均值和最大值,其中ARMS 指标最大值为1.306%,这表明所提方法在概率分布方面的精确性。进一步分析其计算效率,蒙特卡洛模拟法计算时间为2120.72 s,文中所提半不变量计算方法为2.37 s,其计算效率得到较大提高。

表4 电压、流量ARMS指标
4.2 不同拟合方法对比
在得到输出变量的概率分布特性后,为方便后续分析,需要对其概率分布函数进行拟合。表5为采用Cornish-Fisher(CF)级数展开、Gram-Charlisher(GC)级数展开、最大熵法拟合概率密度函数得到的ARMS指标平均值和最大值,其中,采用最大熵法拟合的ARMS 指标最小,即拟合精度更高。图3 为采用不同拟合方法得到的流量概率分布曲线,从图中分析可得,采用Gram-Charlisher 级数展开进行拟合时在首尾两端与蒙特卡洛模拟结果相差较大,其主要原因在于输出随机变量的三阶矩或四阶矩超出一定范围,使所得的概率密度函数出现负值,导致结果不满足基本的概率公理,这将带来较大拟合误差,而采用Cornish-Fisher 级数展开和最大熵法拟合时精度明显更高。
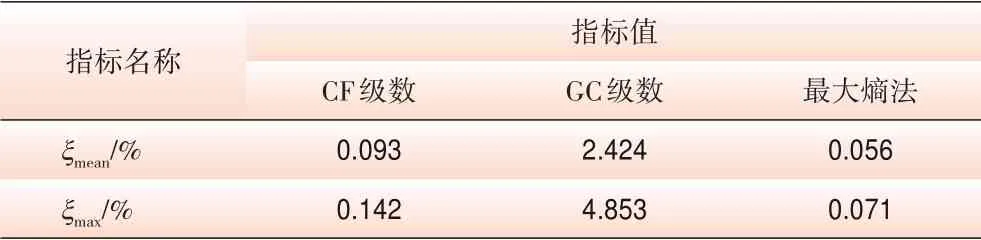
表5 采用不同方法拟合的ARMS指标
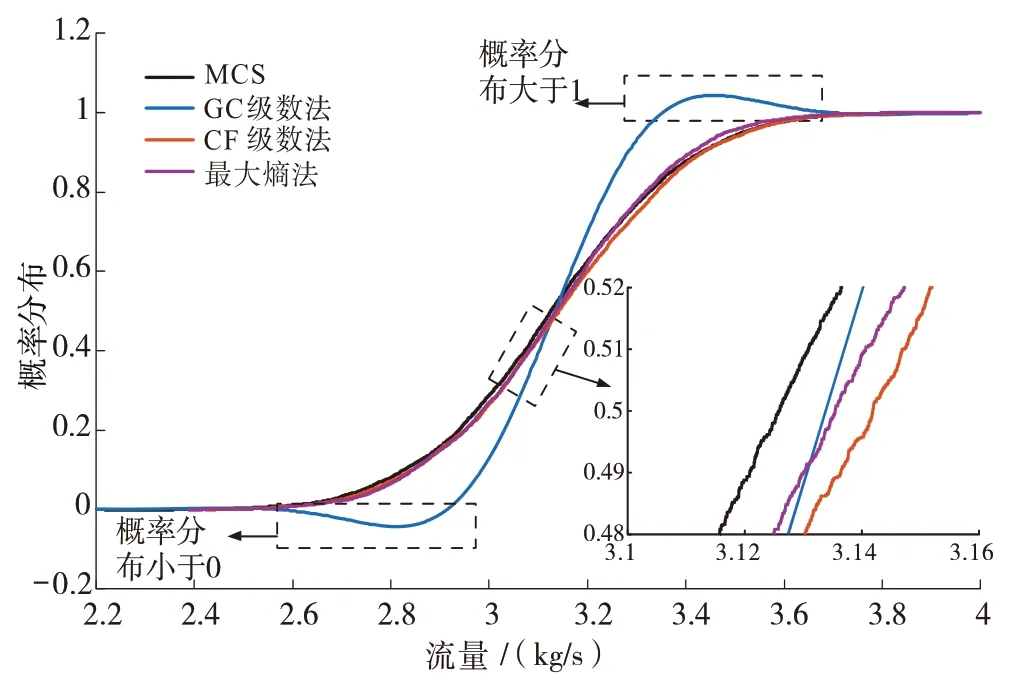
图3 不同方法拟合流量概率分布曲线
4.3 不同概率潮流计算方法对比
将文中所提广义半不变量法与现有同类概率潮流计算方法进行对比,系统参数设置与4.1节相同,其他算法包括拉丁超立方采样LHS[4]和点估计法PEM[5],所得结果对比如表6所示。
由表6 中数据分析可得,文中所提半不变量法的ARMS 指标最大为0.543%,拉丁超立方采样法、点估计法ARMS 指标值最大分别为0.322%和3.526%,其中拉丁超立方采样计算方法精度最高,但是其计算时间远远高于其他两种方法,因此,综合分析计算精度和计算效率两方面,文中所提半不变量法优势较为明显。
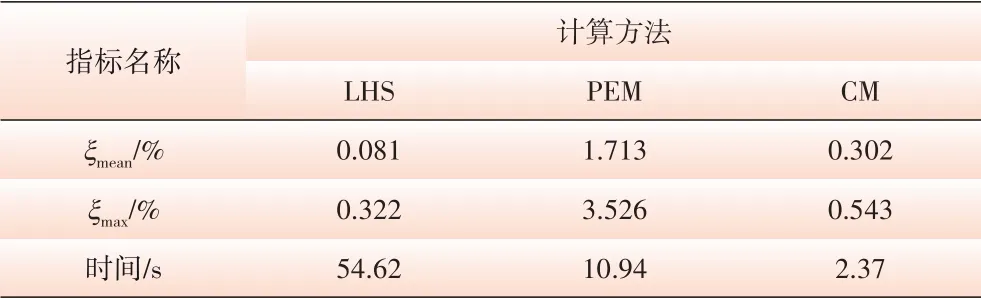
表6 不同方法计算精度及效率对比
4.4 P2H对新能源消纳的影响
随着新能源渗透率不断提高,对其全额消纳将面临巨大挑战。P2H 装置相当于将一部分电能转换为热能存储起来,从而减小了新能源随机性对电网的影响,同时又不造成大规模弃风弃光现象。
图4 为不同功率转化率(即电转热功率与风力发电功率之间的比值)时的电压概率分布曲线。在转化率为0 时,越限概率为47.33%;转化率为0.25时,越限概率为8.01%;转化率为0.5 时,越限概率为0.82%。当提高转化率时,可以明显降低新能源的波动对电压越限的影响,从而可进一步提高新能源的消纳能力。
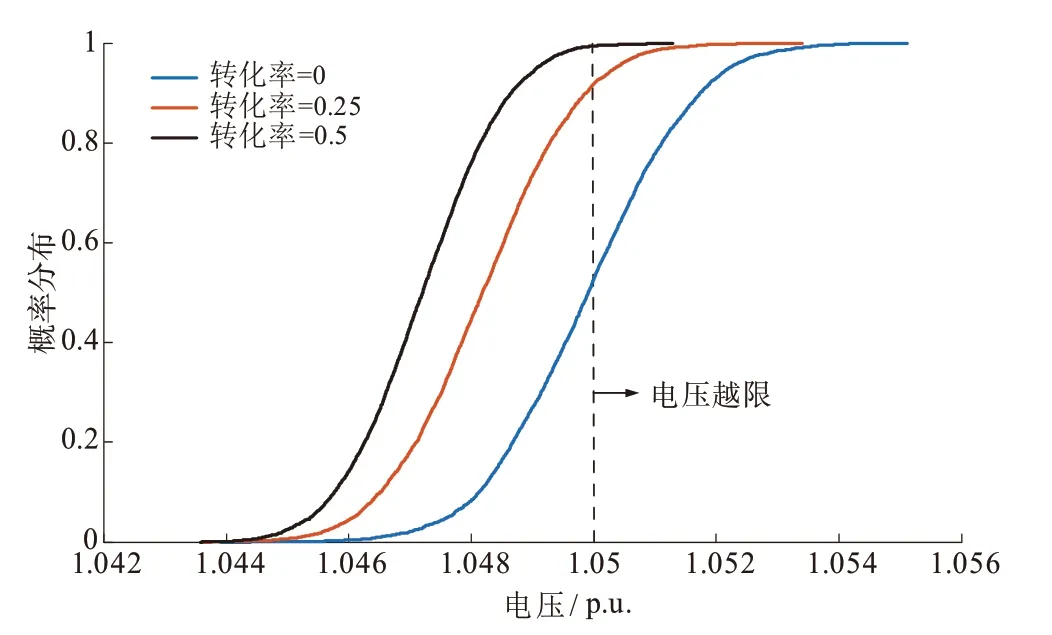
图4 不同P2H转化率时的电压概率分布曲线
5 结语
文中构建了电-热综合能源系统稳态潮流模型,考虑了接入风电和负荷随机性对系统输出变量的影响,提出了一种考虑输入变量随机性的电-热综合能源系统概率潮流计算方法,并在巴厘岛和改进的电热综合能源系统中进行了测试分析。主要结论如下:
1)所提半不变量法在电-热综合能源系统概率潮流计算中具有准确、高效的优点。
2)相对于GC 级数展开和CF 级数展开,采用最大熵法拟合输出变量的概率密度函数更加精确。这为选择最优拟合方法提供理论参考。
3)当提升P2H 的电转化率时,可有效的减小新能源波动给电网带来的影响,从而可促进新能源的进一步消纳。
4)通过文中方法能准确获得电-热综合能源系统输出变量的概率特性,这为进一步研究,如风险评估、鲁棒优化等,提供了有力的理论支撑。
