脉动输出型大功率级联储能变流器的新型拓扑研究
2022-03-23张新刚范瑞祥
张新刚,王 潇,安 昱,张 扬,范瑞祥
(1.特变电工股份有限公司,新疆 昌吉 831100;2.南昌工程学院电气工程学院,江西 南昌 330099;3.国网江西省电力有限公司电力科学研究院,江西 南昌 330096)
0 引言
高压大功率脉冲动力变换器是一种特殊的储能变流器,一般应用于磁悬浮装置、电磁弹射器和电磁轨道炮等需要瞬间加速的工业场合。这类场合的电机一般为永磁同步直线电机,功率可达到100 MVA以上;功率因数较低,无功功率远远大于有功功率;加速过程应当保持恒转矩,以达到更平稳的瞬态特性。以上特点决定了高压大功率脉冲动力变换器的技术与常规采用超级电容的储能变流器[1-2]在拓扑结构和控制上存在较大区别。
现有的储能变流器有多种拓扑结构。近年来,基于多电平技术高压大容量的变流器在我国工业市场中应用越来越广泛,显著提高了工业生产的效率[3]。传统三电平背靠背变流器的控制系统需要分为两部分,即三电平的整流器控制和逆变器控制,这使控制方式变得复杂[4]。文献[5]提到的基于二极管箝位型三电平变换器因其控制效果较好、控制方法较为成熟、实现简单等优点而被广泛应用于轧钢、铁路、矿井等中压大功率场合。但是由于二极管特性参数不一致会导致所串联的二级管电压存在偏差,而偏差太大会造成二极管器件损坏[6-7],因而需要均压措施和RC吸收电路,但这又导致系统体积庞大,成本增加。
这些拓扑结构从原理上也可以应用于高压大功率储能变流器,但是由于功率过大,传统拓扑不区分有功功率和无功功率,电池容量极大、数量极多,造成经济性和可靠性都很低,因此需要一种新的拓扑来降低成本,优化储能配置。文中在级联H桥拓扑、增加超级电容和限流电感的基础上对功率模块进行了进一步的优化设计。
传统储能变流器充电阶段采用不控整流的方式[8-9],输出功率不可主动控制,文中所提变换器在采用不控整流与排序均压相结合的方式,可极大改善输出波形,且输出功率可控,并将有功功率与无功功率区分开来。传统储能变流器通过以下控制策略驱动电机:恒压频比控制(V/F)、矢量控制以及直接转矩控制。恒压频比控制方式是在控制过程中保持电压与频率比率近似不变[10-11];矢量控制比其他两种控制完善得多,调速范围宽,起动力矩高,精度高,响应快;高精度调速都采用矢量控制变流器(SVPWM)[12-13];文献[14-15]所述直接转矩控制(DTC)与矢量控制相比,被控量为转矩,但直接转矩控制在高频运行和低频运行时的实际性能都不如矢量控制。为了实现充电放电过程中的稳定,在新的拓扑下,传统储能变流器的启动电路、主电路和控制策略都要发生相应改变。
基于此,文中研究了新型高压大功率脉冲动力变换器的拓扑结构,并给出关键器件的设计依据。通过理论计算和仿真,验证了启动、充电和电机控制过程的暂态特性。
1 脉冲动力变换器的拓扑结构及原理
1.1 变流器系统结构
传统的T 型三电平大功率储能变流器功率单元拓扑,如图1所示。
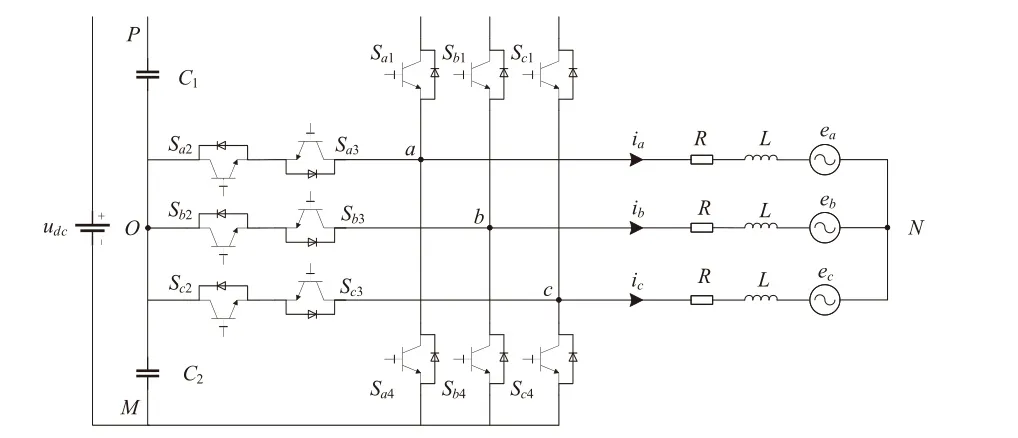
图1 传统的三电平变流器拓扑
针对上述存在的问题,对传统的拓扑进行改良,采用级联多电平结构的储能变流器,系统结构如图2所示。将运行过程分为充电和放电,充电时将电能经H桥整流并储存至超级电容,放电时,储能变流器经H桥逆变输出为六相永磁同步直线电机供电,电机连接固定机械负载,可以恒转矩也可以恒功率启动并运行。每相包括移相隔离变压器,进线端为三相交流电。

图2 六相储能变流器系统结构图
换流链结构如图2(a)所示,其中每个功率单元由超级电容、限流电感、薄膜电容和H桥八部分组成。模块通过超级电容储能,超级电容选用标准模块电容以降低成本。为了限制超级电容的放电电流,在超级电容与H 桥薄膜电容间串联了电感L 以限制超级电容放电电流[16]。薄膜电容从超级电容接收有功能量,与负载进行无功能量交换。
1.2 主电路参数设计方法
1.2.1 换流链模块数计算
电机加速过程中,超级电容电压一直下降,需要保证在电机加速到最高点时,超级电容仍然能够向薄膜电容中注入足够的能量,故超级电容组与薄膜电容间需要有足够的电压差[17]。
星形接线变流器调制比m为:

式中:n为模块数;UφN为网侧电压;Vdc为换流链直流电压;uaN为放电电压;vdc为超级电容电压;m为调制比。即:

考虑到死区、延时等的影响,空载调制比m最大值一般取0.85,因此可得:

1.2.2 超级电容容值计算
超级电容容值为C0,直线电机的容量为SN,功率因数为cosφ,则有功功率可以表示为P=SNcosφ。
因此,储能能量Wall可以表示为:

因此每个功率单元模块内超级电容组的储能WC0为:

而储能的基本公式为:

超级电容的电压和电流满足:

该设计超级电容组充满后电压为vc0_max,最低放电电压为vc0_min,考虑到电容会存在容值下降,假设下降系数为β,综合式(5)和式(6),可得修正后的电容公式为:
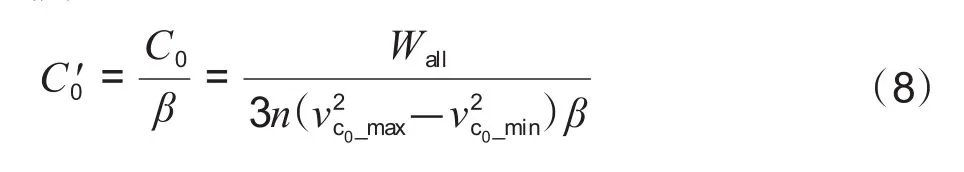
1.2.3 限流电抗器与薄膜电容的计算
超级电容放电需串联限流电抗器限流,为防止电抗器饱和,采用干式空芯电抗器,电抗器数值可根据式(6)和式(7)得出,则有:式中:α表示电抗率;Svn表示超级电容额定容量;f为频率;URMS为每个相单元相电压有效值,考虑了1.3倍的过流。

从超级电容输送到薄膜电容的均为有功功率(损耗忽略),IRMS为相电流有效值,cosφ为功率因数,故每个相单元有功功率为:

开关频率为fSF,则平均每个脉冲能量为:

薄膜电容最大放电电压为vc1_max,最低放电电压为vc1_min,可得C1

从无功功率Q方面考虑,电容与电机线圈电感之间需要进行能量交换。薄膜电压为uc1_dc,其电压波动为Δuc1_dc,则
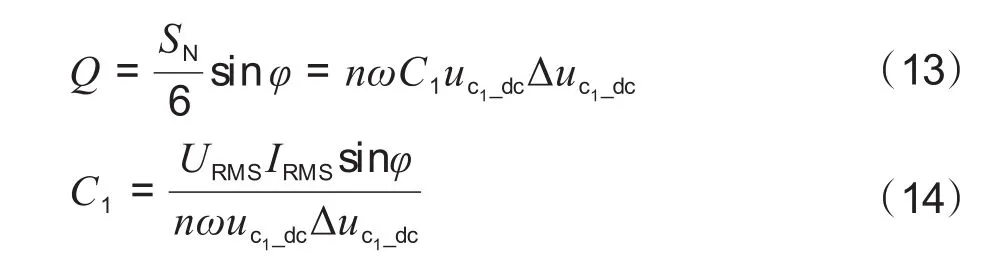
根据式(12)和式(14)可得出所需薄膜电容范围取值。
2 脉冲动力变换器的充电放电控制策略
所提变换器采用排序均压的方式进行充电,在前200 s内保持不控充电,之后切换成排序均压充电。功率模块的排序均压原理是:首先检测桥臂中所有SM 的电容电压并对其进行排序,设uci按增序排列;根据iarm方向,选择电容电压最低/最高的Non个功率模块投入,其余模块切出,以维持桥臂电压均衡[18]。功率模块排序均压原理如图3所示。

图3 功率模块排序均压原理
由桥臂参考电压变换引起的子模块投切(开关频率下限值)以及电容电压均衡所需的功率模块投切共同组成了功率模块前后两个控制周期Tk和Tk+1的投切。令桥臂电流iarm方向为正,功率模块的投入/切出状态如图4所示。

图4 控制周期Tk和Tk+1的功率模块投切
图4中控制周期Tk+1存在两种情形,当Tk和Tk+1两个控制周期导通的模块数和nref(Tk)+nrefTk+1>N时,功率模块的投切如图4(a)所示,当nref(Tk)+nrefTk+1<N时,功率模块的投切如图4(b)所示。排序均压算法通过上述的方式,实现了对功率模块的充放电控制,最终所有子模块电压趋于一致[19]。
3 仿真验证
3.1 启动充电仿真
主回路参数如表1所示,全桥型模块运行于交流侧充电模式时,交流启动100 Ω 电阻和15 mH 电抗器串联的充电回路;不控充电阶段一直带启动电阻;不控充电阶段稳定后切除启动电阻;此后带着电抗器进行排序均压充电。

表1 主回路参数
充电时各模块电压和电流变化如图5所示。
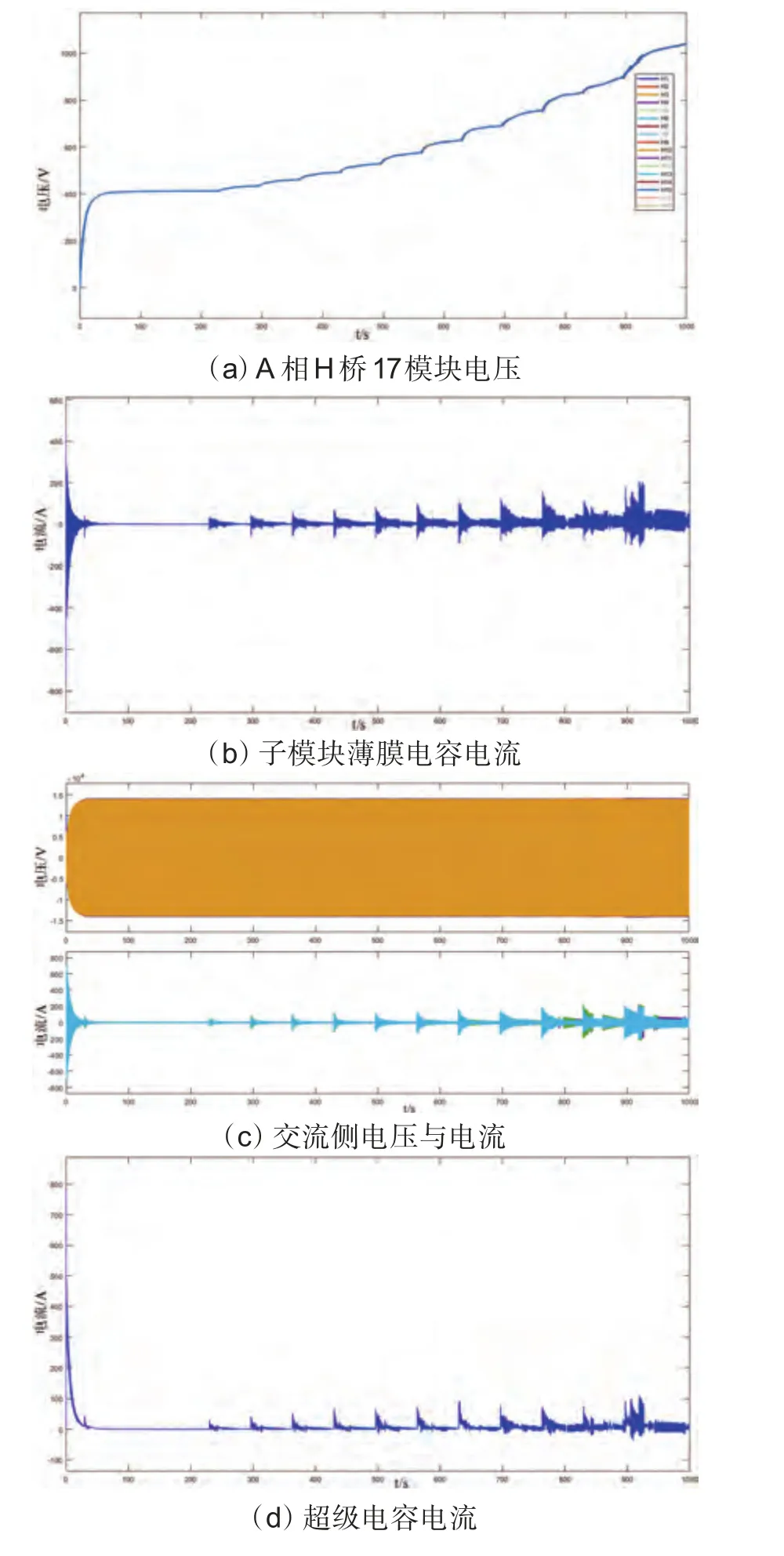
图5 充电时各模块电压与电流
如图5(a)所示,整个充电过程分为四个阶段:1)不控整流充电,全桥模块充电,带启动电阻、电抗器。2)不控充电稳态,切除启动电阻,保留电抗器。3)可控充电阶段,根据电压排序结果,对电压较高序列的模块进行处理。4)可控充电稳态,平均电压大于1100 V 后,停止排序充电,并切除充电电抗器。图5(b)中,薄膜电容上的最大电流约210 A 左右。图5(c)中,220 s前不控充电,220 s后切除软启电阻,进行排序可控充电;220 s时,切除软启电阻,冲击电流约100A;300 s开始切除电压高的模块,冲击电流最大约200 A。每增加一次切除数,则出现一次电流冲击峰值。图5(d)中,超级电容电流最大约为120A。
3.2 电机运行仿真
交流充电完成后,切除充电电阻,并且转入电机并网启动过程。电机给定的转速从0开始启动,因此,采用转矩指令加电流矢量的方案时,需要给转矩一个斜坡指令,使得电流缓慢上升。运行时的电流和电压波形如图6所示。
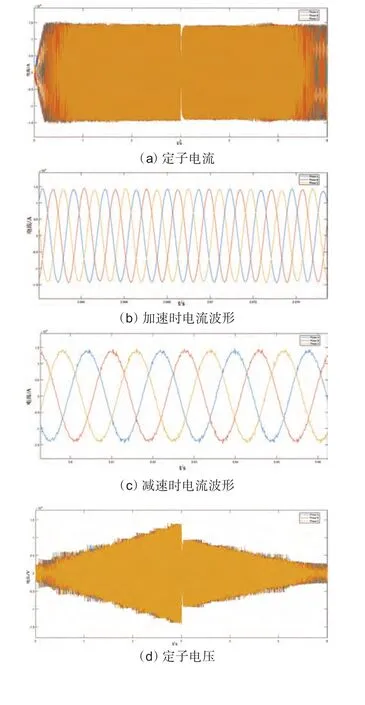

图6 运行时的电流和电压波形
图6(a)中,定子电流幅值保持在14140 A 左右,结合图6(b),在0~3 s,加速时定子电流频率提升到700 Hz,加速过程存在轻微电流幅值上升。图6(c)中,3~6 s时,降速过程中定子电流频率下降至50 Hz左右,此时可停机。
运行时薄膜电容与超级电容电流波形如图7所示。

图7 运行时薄膜电容与超级电容电流波形
图7(a)中,流过薄膜电容C1的电流稳态幅值约为14000 A 左右。图7(b)中流过超级电容C0的电流稳态幅值最大约为900 A 左右。0~3s转速加速电流上升,3~6 s转速下降,处于回馈状态,电流出现正值800 A。
4 分析与讨论
通过已有的拓扑对比传统储能变流器与所提脉冲动力变换器,得到如表2所示的结果。综上所述,可知所提变换器不仅仅在器件数量及容量上节省了成本,还区分了有功和无功功率,能稳定储存能量的同时,在运行电机阶段也能提供稳定的电流。

表2 传统储能变流器与所提变换器的功率单元对比
5 结语
文中围绕高压大功率脉冲动力变换器系统的可靠运行,与传统的背靠背变流器相比,所提出的基于级联H 桥的脉冲动力变换器在功率单元上节省了开关器件的数量,降低了储能电容的容值,大大节省了成本;并通过排序均压算法,实现充放电过程中各个子模块超级电容电压稳定;最后通过仿真对所提方法进行了验证。
