基于调制函数的振动力学模型全参数估计
2022-03-23陈宇宁吴建民
陈宇宁, 吴建民, 田 杨
(1.上海工程技术大学 机械与汽车工程学院, 上海 201620;2.沈阳理工大学 机械工程学院, 辽宁 沈阳 110159)
应用力学模型进行系统的力学特性分析,是揭示系统振动规律从而进行结构设计与改进的重要方法,而获得精准的动力学模型参数是建模过程的关键技术。为此,学者们针对动力学模型参数估计进行了相关研究。孔令毅等[1]应用增广最小二乘法完成了动力学模型参数的无偏估计。王茜等[2]联合全相位FFT和最小二乘法建立了电机叶片的振动参数估计模型。吴超等[3]搭建了电磁轴承-柔性转子系统实验平台,并基于模态实现了动力学模型的参数辨识。高轩等[4]采用分步辨识法建立系统力学蚕食辨识模型。魏青轩等[5]将离散频谱校正和最小二乘联立,推导了以加速度信息为输入的系统参数辨识模型。李新广等[6]结合了Fourier级数方法和最小二乘法辨识出非线性动力学模型中的刚度与阻尼。商兴莲等[7]利用多体系统传递矩阵法识别出机床动力学参数值。
上述方法通过实验或理论方法进行了动力学参数的估计,然而上述方法没有实现刚度、阻尼和力的全参数估计,课题组基于调制函数法提出了一种具有通用性的动力学参数辨识方法,通过该方法可实现动力学全参数的估计。
1 动力学模型参数估计
振动分析过程经典力学将系统视为如图1所示的力学模型。
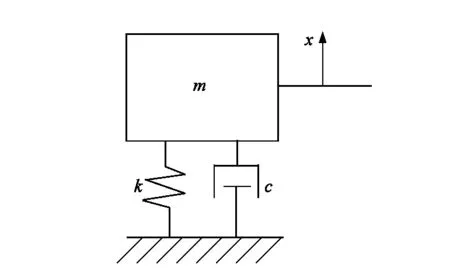
图1 动力学系统模型Figure 1 Dynamic system model
上述动力学模型可描述为[8-10]:
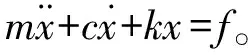
(1)
式中:m为质量,c为阻尼,k为刚度系数,f为作用力。
由于加速度传感器便于布置,且其为相对式仪器,基于加速度信息估计动力学模型参数,则有:

(2)
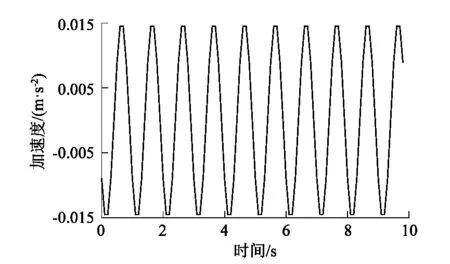
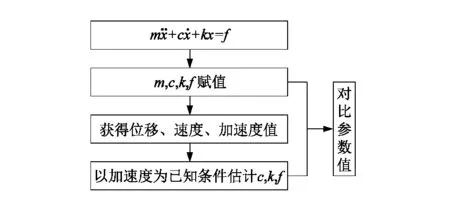
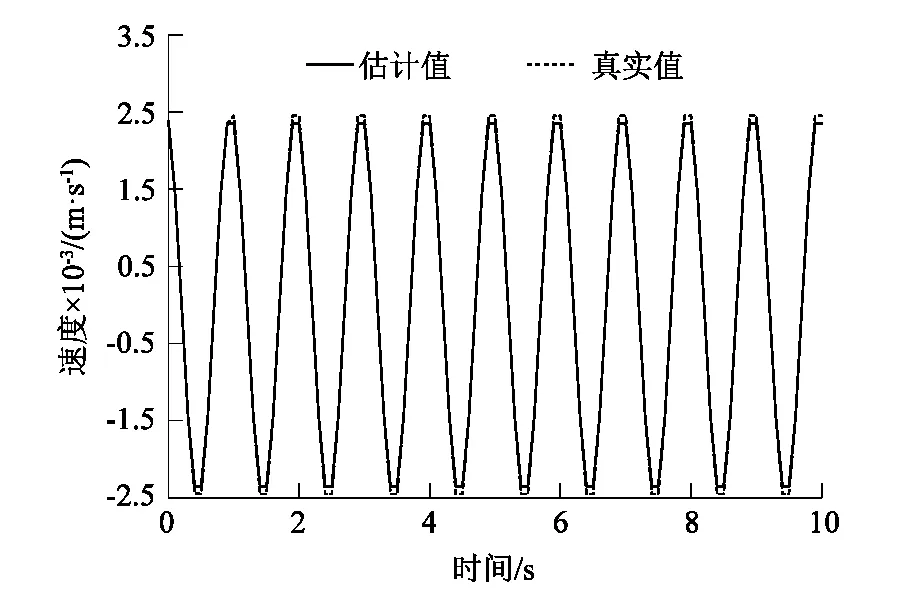
设T (P1)∶g∈Cl([t-T,t]); 式中:t为时间,T为任意小于时间t的常量。 (3) 式中:τ为在定义域内的参数,pj为幂函数,ρj为对应阶次的常数。 然后将模型近似如下: (4) (5) 在式(5)中使用分部积分可得到: (6) (7) 根据调制函数gi的性质,其未知边界值可以被消除,因此,对于i=1,…,N,可以得到: (8) 其中: Aλ=b。 (9) 式中b为常向量。λ=(c,k)T,A∈RN×2和b∈RN如下: 式中i=1,…,N。 式(9)可以用最小二乘法求解,得: λ=(ATA)-1ATb。 (10) 为了估计参数力f,课题组考虑雅克比正交基,定义在[0,1]上的雅克比正交多项式如下: (11) 式中μ,κ∈[-1,+∞]。 令函数f和g是属于C([0,1])的函数,然后是标量积〈·,·〉μ,κ函数的定义如下: (12) 式中ωμ,κ(τ)=(1-τ)μτκ是相关的权重函数,因此可以获得: (13) 如果f∈C([t-T,t]),其可以用下面的雅克比正交级数来表示: (14) 为了验证上述模型的准确性,课题组应用MATLAB编制了式(1)动力学方程的计算程序,通过代入已知作用力,已知动力学模型参数刚度k、阻尼c和作用力参数f,计算出在此作用力f下的位移、速度和加速度: f=F0sinωt。 (15) 式中F0为常力。 系统动力学模型中部分参数如表1所示。 表1 力学模型参数Table 1 Mechanical model parameters 通过计算可获得模型的位移、速度和加速度信息,而课题组提出的估计模型是以加速度信息作为输入的,因为在布置传感器的过程中,加速度传感器更容易完成装配,计算出的加速度信息如图2所示。 图2 加速度真实值Figure 2 True value of acceleration 在已知加速度的前提下,将模型真实参数刚度k、阻尼c和作用力参数f作为未知参数,应用式(2)~(13)估计得到刚度k、阻尼c和作用力参数f,再将估计值与真实值进行对比,从而验证参数辨识模型的正确性,具体验证过程如图3所示。 图3 估计方法验证流程Figure 3 Estimation method validation process 按照图3的流程通过仿真估计出参数:k=3.85×107N·m-1;c=4.59×104N·s·m-1;f=14 750 sinωt。仿真估算得到k,c,f,与表1中的真实值对比,误差分别是1.3%,2.0%和1.7%。 为了进一步直观地对比课题组提出估计模型的准确性,课题组将估计出的参数代入式(1)中重新计算出系统速度和位移的估计值,图4所示为速度的真实值与估计值对比结果。 图4 速度的真实值与估计值对比Figure 4 Comparison of real and estimated speed 图5所示为位移的真实值与估计值对比结果。 图5 位移的真实值与估计值对比Figure 5 Comparison of real and estimated displacement 通过对比可知:在应用估计出的参数进行动力分析的估计值与真实值重合度较高,其趋势重叠且振动幅值误差较低,因此证明课题组提出估计模型具有较高的精度。 课题组以便于获得的加速度信息为输入数据,基于传统动力学模型通过调制函数法建立了振动力学系统的全参数的估计模型,所提出的方法将微分问题转换为积分问题,大大降低了求解的误差,通过估计值和真实值得对比,其综合平均误差为1.67%,通过课题组提出的估计模型,可实现振动力学参数无法测量前提下的系统建模,从而开展相关的力学状态分析。
(P2)∶g(k)(t-T)=0;
(P3)∶g(k)(t)=0。1.1 刚度和阻尼参数估计

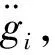
1.2 参数力f的估计
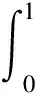
2 模型验证


4 结论
