线性描述系统有限时间函数观测器设计及存在性讨论
2022-03-23张建成
张建成,王 艳
(1.江南大学理学院,江苏无锡 214122;2.江南大学物联网工程学院,江苏无锡 214122)
1 引言
在现代控制领域,状态反馈发挥着重要作用.该控制策略要求系统状态是可测量的.而在实际控制系统中,作为系统内部变量的状态往往是不可测量或不完全可测量的.状态观测器的出现很好地解决了这一工程需求和物理上不可实现之间存在的矛盾[1].自20世纪60年代以来,观测器理论已经取得了丰硕的成果,诸如未知输入观测器[2-8]、滑模观测器[9-12]、区间观测器[13-17]、函数观测器等[18-19].
由于在状态反馈中只需要用到系统状态的线性函数,因此在基于观测器的控制设计中,相比普通状态观测器,函数观测器更具有优势,因为它在能够提供系统所需控制信号的同时,又不需要估计系统的全部状态[18].近几十年来,函数观测器理论一直是控制领域研究的热点问题[19-32].例如,在文献[19]中,Darouach 研究了线性系统函数观测器设计问题,给出了函数观测器存在的充分条件.在其最新的论文[20]中,该作者及其合作者推广了文献[19]的结论,给出了更一般化的函数观测器存在的充要条件.在文献[22]中,Fernando等人引入了函数可观/函数可检测(functional observability/functional detectability)的概念,并指出系统满足函数可观/函数可检测是函数观测器存在的充分条件.随后,Jennings等人从特征空间的角度对函数可观这一概念给出了新的判据[23].此外,Rotella等人针对满足函数可观的系统提出了构造函数观测器的新方法,其不依赖于Sylvester方程的解,也不需要将系统化为状态空间标准型[24-25].随后,该论文的方法和结论被推广到含有未知输入的系统中[26].文献[27]研究了一类时变系统,给出了一种基于参数化方法计算增益矩阵的函数观测器设计方法.文献[28]针对含有时变时滞的系统讨论了滑模函数观测器设计,基于Lyapunov-Krasovskii 和线性矩阵不等式理论给出了观测器存在的充分条件.此外,近年兴起的区间观测器理论因其能够在较弱的条件下估计出状态所处的区间这一优势而备受关注,其中函数区间观测器理论也引起学者们的关注,如文献[29-31].最近,基于T-S模糊系统的方法也被用于非线性系统函数观测器设计中[32].需要指出的是,上述文献中对函数观测器设计和存在条件的研究均是对标准的一般系统展开的,而据笔者所知对描述系统函数观测器的研究在已有的文献中(除文献[34-35]外)还鲜有报道.
描述系统,又称奇异系统、广义系统、微分代数系统,是一类更具一般性的动态系统.描述系统在刻画带有代数约束的系统时更具有优势,其在电路系统、生态系统和机械系统的建模中已经得到广泛应用[33].近年来,描述系统观测器理论得到了较大发展,已经有很多成果报道出来.但对描述系统函数观测器的研究却少之又少,目前仅有文献[34-35].文献[34]针对一个线性描述系统构造了Luenberger类型的渐近收敛函数观测器,并以矩阵秩条件形式给出了观测器存在的充要条件.随后,该作者在文献[35]中再次对该描述系统函数观测器设计问题展开研究,其观测器存在条件以线性矩阵不等式的形式给出.注意到,无论是文献[34]还是文献[35]其存在性条件都不仅用到了系统的原始矩阵,还用到了一些中间变量,故该条件不易检验.因此,探索新的能仅用系统原始矩阵表征的观测器存在条件在理论和设计实践中都有重要意义.
另一方面,注意到上述文献无论是针对一般系统还是描述系统的研究其函数观测器都是渐近收敛的.该类型观测器基于Lyapunov稳定性理论设计得到.因此,无论是观测器的估计精度还是收敛时间都依赖于观测器增益和原系统初始条件.由于实际系统的初始条件很难获得,很难通过调节观测器的初始值来提高观测器的精度和收敛速度.然而,在许多实际应用(如导弹制导过程[36])中,初始条件未知但为了满足控制要求,需要在规定的时间内获得性能良好的状态估计.在这种情况下,设计了一个收敛时间可自由调节且不受初始条件影响的观测器是很有意义的.在这一方面,近年来已经有一些成果报道出来.2002年,Engel等人针对满足能观性的线性系统提出一种有限时间观测器设计方法[37].该方法通过构造两个结构上完全相同的渐近收敛观测器在几乎任意给定的时间内实现了对系统状态的精确估计.随后,该方法被推广应用到含有未知输入的系统和描述系统中[38-42].需要指出的是,尽管有限时间观测器理论在状态观测器设计方面已有不少结果,但在函数观测器设计方面还没有见诸报道.
基于以上讨论,本文针对线性描述系统提出一种有限时间函数观测器设计方法,并给出在形式上能用系统原始矩阵表征的观测器存在条件.本文的主要贡献和创新之处可总结为:1)给出了描述系统有限时间函数观测器设计框架,并实现在任意规定时间内的精确估计.2)与经典的渐近收敛观测器不同,本文提出的有限时间观测器其无论是收敛时间还是估计精度都不受到原系统初始条件的影响.3)用系统原始矩阵给出了描述系统函数观测器存在的充分必要条件.
本文其余部分安排如下:第2节为问题描述和一些预备知识.第3节具体给出有限时间函数观测器的设计方法和存在性讨论.第4节给出仿真结果验证本文方法的有效性.最后,在第5节给出结论.
2 问题描述与预备知识
考虑如下的线性描述系统:

其中:x ∈Rn,y ∈Rp和u ∈Rm分别为系统状态,可测输出和控制输入.z ∈Rr为待估计的未知向量.E ∈Rℓ×n,A ∈Rℓ×n,B ∈Rℓ×m,C ∈Rp×n和L ∈Rr×n为常数矩阵.不失一般性,假设rankE 针对系统(1),文献[34]研究了渐近收敛函数观测器的设计方法和存在条件,其对应的r维函数观测器存在条件为 注意到条件(2)-(3)中不但包含了系统(1)的原始矩阵E,A,C,L还涉及到了一些中间过渡变量E⊥,Γ+,α和β.这给观测器存在性的检验造成了一定困难. 针对系统(1),本文研究可以在任意设定时间内达到对函数z=Lx精确估计的有限时间函数观测器设计方法,并探索得到可以直接由原始矩阵E,A,C,L表示的存在条件,以克服文献[34]给出的存在条件在验证过程中的缺陷. 为便于以下讨论,对使用到的符号先进行约定.符号I代表单位矩阵,In为n×n维的单位矩阵.对于矩阵A,λi(A)表示该矩阵的第i个特征值.X ⇔Y意为X等价于Y.E⊥表示满足E⊥E=0的具有最大行数的行满秩矩阵.对于任意矩阵Θ,Θ+表示Θ的广义逆并满足ΘΘ+Θ=Θ.特别地,对行满秩矩阵Θ有ΘΘ+=I. 本节先给出系统(1)的有限时间函数观测器设计框架,然后对存在条件进行详细讨论,并给出可以直接由原始矩阵E,A,C,L表示的存在条件.最后,对本文和文献[34]给出的具有不同形式的观测器存在条件之间的关系进行讨论. 方程(1a)左右两端左乘矩阵E⊥可得 将式(1b)和式(4)写成一个整体 这样,基于新的输出信号(5),系统(1)可写为 受文献[37]的启发,为了设计有限时间函数观测器,需要对系统设计两个结构完全相同的渐近收敛函数观测器.为此,对于系统(6)假设存在矩阵Pi,Mi(i=1,2)使得PiE+Mi=L.这样,本文给出具有如下形式的渐近收敛函数观测器: 对于系统(1),设计如下形式的有限时间函数观测器: 则系统(11)-(12)为系统(1)的有限时间函数观测器,即对于任给的d>0,有ˆz(t)≡z(t),t≥t0+d,其中t0为初始时刻. 注1对于系统(1)文献[34]给出了目标函数z=Lx的渐近估计.但其估计精度和观测器收敛时间均依赖于观测器极点配置和原系统与观测器之间的初始误差,因此无法提前设置.相比之下,本文提出的有限时间函数观测器方法其收敛时间可以根据需要自由设定且与初始条件无关. 注2需要指出的是,尽管在理论上收敛时间d>0可以任意设置.但在实践中,d不宜设置的过小.事实上,d越接近于0则矩阵越接近于奇异.这将导致在时间到达t0+d之前,观测器的状态过大,可能会对硬件造成损害. 定理1指出,有限时间函数观测器(11)-(12)存在当且仅当存在矩阵Pi,Ni,Mi,Ki,Hi和Qi(i=1,2)满足条件(10)和(13).但条件(10)和(13)涉及很多中间变量,且以矩阵方程和矩阵特征值不等式的形式给出,很难检验.本小节将分别用系统(1)的原始矩阵E,A,C,L给出与条件(10)和(13)等价的条件. 引理1如下陈述等价: I) 存在矩阵Pi,Ni,Mi,Ki,Hi和Qi(i=1,2)满足式(10). II) 对于矩阵E,A,C,L,有 基于以上对有限时间函数观测器存在条件的讨论,给出定理2. 定理2对于系统(1),存在形如式(11)-(12)的有限时间函数观测器,当且仅当条件(18)和(30)成立. 证 结合定理1和引理1-2直接得到定理2的结论. 在第2节已经讲到,对于系统(1)的函数观测器设计问题,文献[34]给出的条件(2)和(3)不但包含了系统(1)的原始矩阵E,A,C,L,还包含了一些中间变量E⊥,Γ+,α和β.而本文给出的条件(18)和(30)仅仅用到了系统(1)的原始矩阵E,A,C,L.因此,相对于文献[34]本文给出的存在条件在形式上更为直观且易于检验. 另一方面,应该指出的是,尽管由于设计方法不同从而导出的观测器存在条件在形式上也不相同,但是本文和文献[34]中条件却是等价的.具体说来,条件(18)等价于式(2),而式(30)等价于式(3).下面将证明这种等价性. 故由式(35)-(36)知(17)⇔(2).由于(18)⇔(17),自然地,有(18)⇔(2). (30)⇔(3):令 注3文献[37]给出了线性一般系统有限时间状态观测器的设计方法和存在条件.而对于有限时间函数观测器设计的研究,在已经发表的文献中还未有过报道.本文首次针对描述系统研究其有限时间函数观测器设计.和文献[37]相比,本文的结果更具有一般性.事实上,若令E=L=In,则系统(1)退化为文献[37]中的系统(1).此时,条件(18)恒成立,而条件(30)退化为(A,C)能观,这恰好是文献[37]中给出的有限时间观测器存在性条件.因此,文献[37]的结果可看作本文的一种特殊情形.另一方面,从观测器结构和存在条件来看本文对观测器结构的探索和存在条件的分析与文献[37]相比则要复杂得多. 注4需要指出,在条件(18)下,系统(1)(或记为系统{A,C,L})为部分脉冲能观的,即仅当z=Lx不含有脉冲时,y亦不含有脉冲[34].这是因为,由条件(18)可知 根据文献[34]中引理5可知{A,C,L}为部分脉冲能观.特别地,当L=In时,上述条件退化为 此条件正是标准的脉冲能观的充要条件[43]. 最后,本文将有限时间函数观测器(11)-(12)的设计步骤总结为算法1. 算法1 1) 检查式(18)和式(30)是否满足.若是,进入下一步;否则,观测器设计失败. 2) 计算矩阵Σ,Υ和Π1,Π2,选取Z1和Z2满足式(13). 3) 选取d>0,计算矩阵 4) 构造有限时间函数观测器(11)-(12). 本节给出两个例子来验证本文所提方法的有效性,并通过和传统方法作比较以显示本文方法的优势. 考虑系统(1)[34]其系统矩阵分别为 针对该系统,文献[34]设计了具有如下形式的渐近收敛函数观测器: 图1给出了z(t)的真实值(图1中绿色实线)和由函数观测器(38)得到的估计值(图1中蓝色虚线).可以发现,函数观测器(38)的确可以实现对z(t)的渐近估计,但要得到较为精确的估计效果需要时间t≥5 s.为了更为快速地得到z(t)的估计值,下面根据本文算法设计有限时间函数观测器. 对于该系统,经检验,其存在条件 对任意复数s均成立.根据算法1,相关矩阵计算如下: 由以上矩阵根据算法1构造有限时间函数观测器(11)-(12). 对函数观测器(11)-(12)设置初值¯z(0)=[-30-20]T.为了将本文提出的有限时间函数观测器和文献[34]的观测器观测效果作比较,不失一般性,本文设定观测器收敛时间分别为d=0.5,1,2,3.为了方便比较,将4种收敛时间下的观测结果一并画在图1中.仿真结果表明,文献[34]的函数观测器方法和本文方法均能实现对z(t)的估计.但是,本文方法可以任意设定观测器的收敛时间,而文献[34]的方法不能.另一方面,为了比较两种观测器的估计精度,将他们的估计误差展示在图2中.由图2知,对于文献[34]设计的的观测器,只有当时间t≥5 s后估计精度方可,而在初始的5 s内估计精度较差.而同样在初始的5 s内,对于本文提出的有限时间观测器而言,所预定的时间(d=0.5,1,2,3)一旦达到,观测器误差可即时收敛到0. 图1 文献[34](即[Darouach,2012])和本文方法得到的z的估计(d=0.5,1,2,3)Fig.1 Estimations of z by[34](i.e.,[Darouach,2012])approach and the PTFO approach(d=0.5,1,2,3) 图2 文献[34](即[Darouach,2012])和本文方法得到的z的估计误差(d=0.5,1,2,3)Fig.2 Estimation errors of z by[34](i.e.,[Darouach,2012])approach and the PTFO approach(d=0.5,1,2,3) 考虑如图3所示的电路系统,其中C1和C2表示电容器,R1和R2为电阻器,L为电感器,u=vs为电源电动势.此处,Vc=v1(t)和Vout=v2(t)分别表示C1和C2的电压,i1和iL分别为流经C1和电感L的电流.根据基尔霍夫定律,该电路系统可以由以下状态空间方程描述 图3 电路系统Fig.3 An electronic circuit 定义系统状态为x=[v1v2iL i1]T,测量输出为y(t)=[v1iL i1]T.于是电路系统(39)可以写成系统(1)且其系统矩阵为 假设以上参数分别为C1=100 mF,C2=100 mF,R1=4 Ω,R2=4 Ω,L=0.1 H.为了得到仿真结果,不妨假设电源信号为方波信号vs(t)=8.6square(1.5πt,50). 对于系统(39),容易检验对于任意复数s有 根据定理2,形如系统(11)-(12)的有限时间观测器一定存在,其增益矩阵可计算如下: 然后,由以上矩阵根据算法1构造有限时间函数观测器(11)-(12). 为了将本文提出的有限时间函数观测器和传统的渐近收敛函数观测器估计效果作比较,同时构造传统函数观测器如下: 对于原系统(39),有限时间函数观测器系统(11)-(12)和传统函数观测器系统(40),分别赋初值为x(0)=[3 1 4-4.75]T,(0)=[-2 2]T和ζ(0)=4,其中有限时间函数观测器的预定收敛时间设为d=0.5.图4和图5分别画出了z=Lx的真实值和由两种观测器得到的估计值以及它们的估计误差.从图4和图5中可以看到,当t≥3 s后两种观测器均能获得满意的估计效果.但在t<3 s内,传统的渐近收敛函数观测器无法获得很好的估计效果,而本文提出的有限时间函数观测器依然可以. 图4 由传统方法和本文方法得到的z的估计(d=0.5)Fig.4 Estimations of z by traditional approach and the present approach(d=0.5) 图5 由传统方法和本文方法得到的z的估计误差Fig.5 Estimation errors of z by traditional approach and the present approach(d=0.5) 本文提出的有限时间函数观测器方法还有一个优点,其估计精度和观测器收敛时间不会受到原系统初值的影响.即无论原系统初始值为何值,当预定的时间达到以后,由观测器给出的估计值都可以精确地跟踪到系统的真实值.为了验证这一优点,分别假设原系统初始值为x(0)=[3+j1+j4+j -4.75]T,j=-45,-39,-33,-27,-21,-15,-9,-3,3,9,15.其估计误差请参见图6.图6显示,尽管系统初始值不同,但在预先设定的时间t=0.5 s后,估计误差都将收敛到0. 图6 选取不同初值x(0)时本文方法得到的z的估计误差(d=0.5)Fig.6 Estimation errors of z by present approach for different x(0)(d=0.5) 本文针对线性描述系统给出了一种有限时间函数观测器设计方法.该观测器能在几乎任意给定的时间内达到对目标函数的精确估计.此外,论文着重讨论了观测器存在的充分必要条件,并将存在性条件用系统原始矩阵的形式给出.与已有文献相比,本文给出的结论更加直观,更易于对条件的检验.如何将本文方法和结论推广到网络化描述系统中将是下一步要考虑的问题.
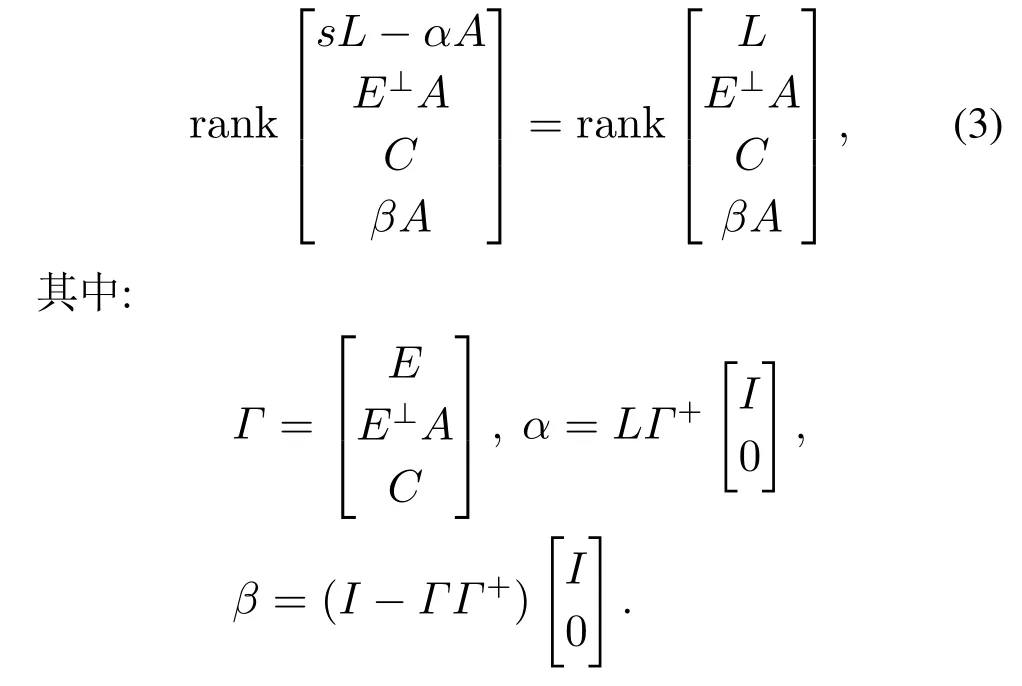
3 有限时间函数观测器
3.1 函数观测器设计






3.2 函数观测器存在条件







3.3 与文献[34]结论的比较



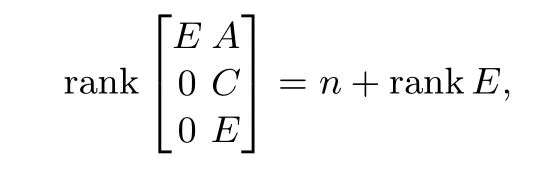
4 数值仿真
4.1 仿真算例1







4.2 仿真算例2
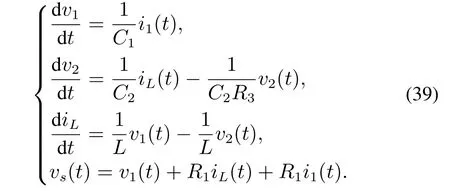





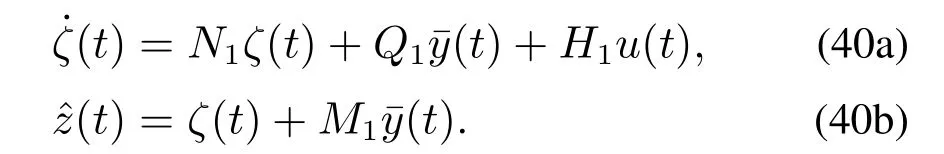



5 结论
