欠驱动水下机器人三维轨迹跟踪有限时间预设性能控制

杜佳璐,李 健

(大连海事大学船舶电气工程学院,辽宁大连 116026)

1 引言

水下机器人(autonomous underwater vehicles,AUVs)在进行水下勘探、海底地形测绘、近海防御和军事侦察等作业任务时,需要自主航行跟踪三维轨迹.轨迹跟踪控制是AUV自主航行的关键技术之一,而AUV存在欠驱动特性、动态不确定性,且遭受未知时变的海洋环境扰动,因此,克服AUV动态不确定和未知海洋环境扰动的影响,实现高精度的欠驱动AUV三维轨迹跟踪控制,具有重要的现实意义.

在欠驱动AUV运动数学模型已知的情况下,考虑未知常值海流扰动,文献[1]应用输出重定义方法处理AUV欠驱动问题,利用轨迹跟踪误差积分补偿海流扰动,基于反馈线性化方法设计了欠驱动AUV轨迹跟踪控制律;考虑未知时变海流扰动,文献[2]应用视线视距法处理AUV欠驱动问题,构造扰动观测器,实时估计扰动,基于滑模控制方法设计了欠驱动AUV轨迹跟踪控制律.同时考虑欠驱动AUV运动数学模型动态参数未知和海洋环境扰动时变未知情况,文献[3]应用视线视距法处理AUV欠驱动问题,利用模糊逻辑系统逼近不确定项,基于逆推方法提出了AUV自适应模糊轨迹跟踪控制策略.文献[1-3]中期望轨迹均为水平面或垂直面上的二维轨迹.

针对欠驱动AUV三维轨迹跟踪问题,在欠驱动AUV运动数学模型已知的情况下,考虑未知时变海洋环境扰动,文献[4]设计了鲁棒控制项补偿扰动,应用滤波反步法设计了欠驱动AUV三维轨迹跟踪控制律.同时考虑欠驱动AUV动态不确定和未知时变海洋环境扰动,文献[5]将模糊逻辑系统和反馈线性化方法相结合,设计了欠驱动AUV三维轨迹跟踪控制律,文献[6-7]将自适应技术分别与逆推方法和动态面控制方法相结合,设计了欠驱动AUV三维轨迹跟踪控制律,文献[8]将神经网络和反馈线性化方法相结合,设计了欠驱动AUV三维轨迹跟踪控制律.

此外,在AUV运动数学模型已知、海洋环境扰动未知时变情况下,文献[9]引入AUV轨迹跟踪误差的分数幂,应用逆推方法设计了全驱动AUV三维轨迹跟踪控制律;考虑AUV动态不确定、海洋环境扰动时变未知的情况,文献[10]将滑模控制方法与逆推方法相结合,设计了全驱动AUV三维轨迹跟踪控制律.文献[9-10]均实现了AUV轨迹跟踪误差的有限时间收敛,提高了AUV轨迹跟踪控制系统的响应速度,然而,欠驱动AUV轨迹跟踪有限时间控制鲜有研究.另一方面,考虑欠驱动AUV运动数学模型参数未知、海洋环境扰动未知时变的情况,文献[11]利用指数收敛的预设性能函数描述AUV轨迹跟踪控制的预设性能,构造误差映射函数,将受预设性能限制的AUV轨迹跟踪误差转变为非受限的变换后误差,基于自适应技术和动态面控制方法设计了欠驱动AUV二维轨迹跟踪控制律,保证AUV轨迹跟踪控制满足预设的瞬态和稳态性能,然而,关于具有预设性能的欠驱动AUV三维轨迹有限时间跟踪控制的研究尚未见报道.

近年来,有限时间控制和预设性能控制受到广泛关注[12-14].有限时间控制是设计有限时间控制律,保证闭环控制系统在有限时间内稳定,常用的方法有误差分数幂方法、齐次系统理论方法和滑模控制方法等,其中,滑模控制方法由于其设计简单、鲁棒性更强等优点应用最为广泛,然而存在固有的抖振问题,文献[15]提出超螺旋(super-twisting,ST)算法,削弱了滑模控制的抖振问题,但并未完全移除[16].预设性能函数可描述预设的系统瞬态和稳态控制性能,预设性能控制是通过设计预设性能函数,并基于此设计预设性能控制律,使系统满足预设性能,然而,传统的预设性能函数不能预先设置收敛到其预设的稳态值的期望时间,导致预设性能控制律不能保证系统控制误差在指定时间内收敛到预设的稳态误差带.

基于上述讨论,针对具有不确定动态和未知时变海洋环境扰动的欠驱动AUV三维轨迹跟踪问题,本文提出新型预设性能函数,可根据系统的性能要求、能力和限制条件预先直接设置AUV轨迹跟踪误差进入并不再超出其预设的稳态误差带所需的期望时间;提出新的ST算法,可移除常规ST算法的抖振问题,基于此,构造ST扩张状态观测器,设计ST控制律;提出欠驱动AUV三维轨迹跟踪有限时间预设性能控制方案.

符号说明:记

其中:sgn(·)为符号函数;tanh(·)为双曲正切函数;ℓ∈R;s(·)和c(·)分别表示正弦函数和余弦函数.

2 问题描述和预备知识

2.1 AUV运动数学模型

如图1所示,定义北东坐标系OEXEYEZE和附体坐标系OBXBYBZB.x,y,z,φ,θ和ψ分别为AUV 在北东坐标系下的纵荡位置、横荡位置、垂荡位置、横摇角、纵摇角和艏摇角,u,v,w,p,q和r分别为AUV在附体坐标系下的纵荡速度、横荡速度、垂荡速度、横摇角速度、纵摇角速度和艏摇角速度.由于AUV的设计结构是主对称轴对称的,AUV横摇运动可被忽略,建立五自由度AUV运动数学模型如下[17]:

图1 北东坐标系和附体坐标系Fig.1 The North-East-Down coordinate system and the body-fixed coordinate system

为旋转矩阵;M=diag{m11,m22,m33,m44,m55}为惯性矩阵;

假设11)矩阵M,C(υ),D和向量G(η)中的参数是不确定但有界的,并记M=Mnom+ΔM,其中:Mnom表示M的标称值,ΔM表示M的不确定部分;2)海洋环境扰动d(t)是未知时变的,di(t)(i=1,2,3,4,5)及其一阶导数是有界的.

2.2 位置坐标变换

为了处理AUV的欠驱动问题,对AUV的位置向量[x y z]T进行如下坐标变换[8]:

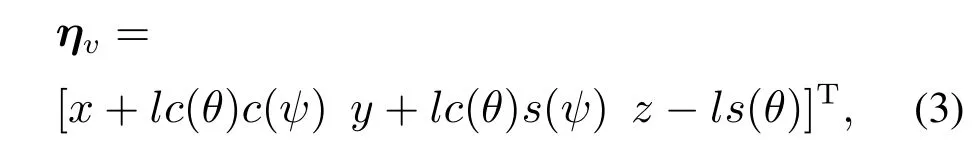
式中l为AUV重心到虚拟控制点Ov的距离,如图1所示.根据式(1)-(3),可得到如下动态方程:

式中:

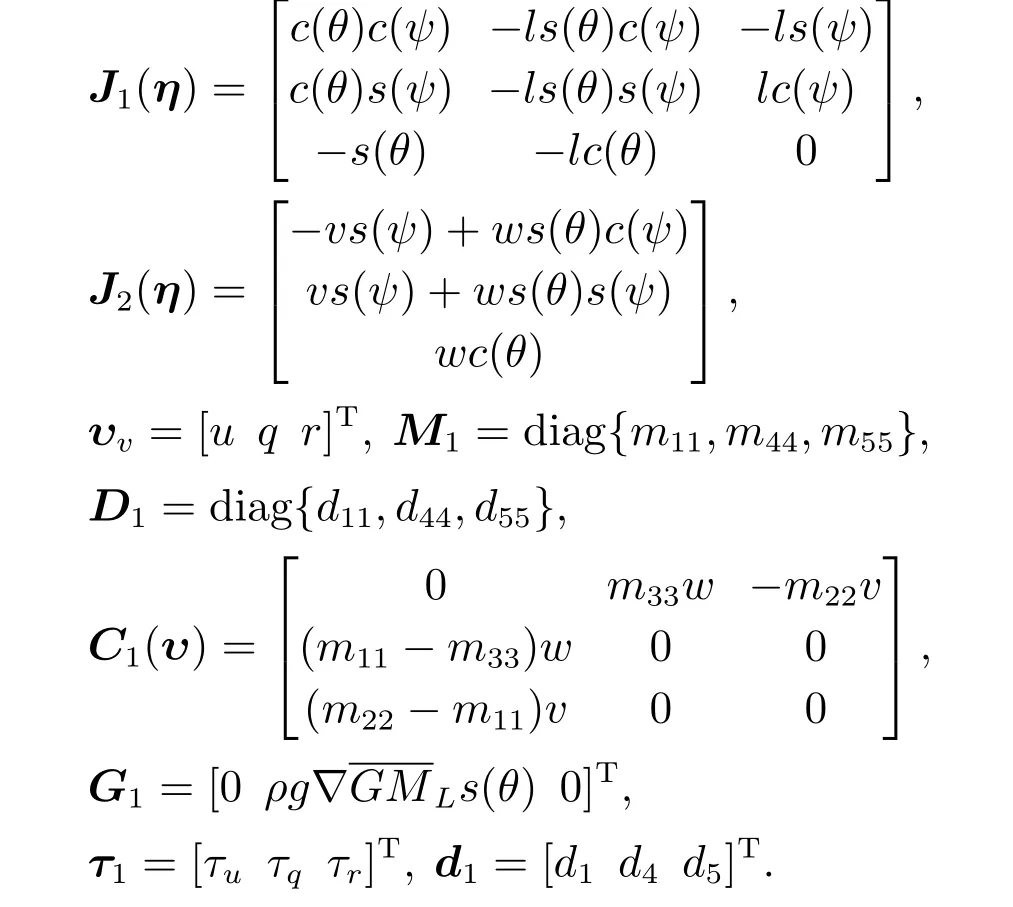
可见,ηv和τ1直接相关,可使得AUV欠驱动问题给轨迹跟踪控制设计带来的困难得以解决.

2.3 新型预设性能函数

定义AUV的轨迹跟踪误差e=[e1e2e3]T

AUV轨迹跟踪控制的预设性能描述如下:

图2 预设性能函数历时曲线Fig.2 The duration curves of prescribed performance functions

本文的控制目标是在假设1下,设计欠驱动AUV三维轨迹跟踪控制律τ1,使得欠驱动AUV虚拟控制点的位置向量ηv在有限时间Tc内跟踪期望的三维轨迹ηd=[xd yd zd]T,同时保证轨迹跟踪误差ei满足式(7)-(8)所描述的预设性能.

假设2xd,yd和zd及它们的一、二阶导数均是光滑有界的.

3 AUV三维轨迹跟踪控制设计

3.1 误差映射函数

提出如下误差映射函数:

为AUV不确定动态和未知海洋环境扰动构成的总扰动.

3.2 ST扩张状态观测器构造

首先,定义滑模面

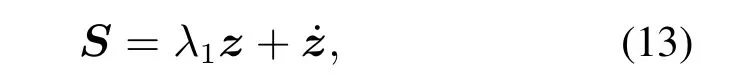
式中λ1为正的设计参数.

根据式(11)-(12),S的导数为

为估计总扰动,依据扩张状态观测器的构造思想,将AUV的总扰动W增广为AUV新的状态向量X,即X=W,可得如下增广系统:

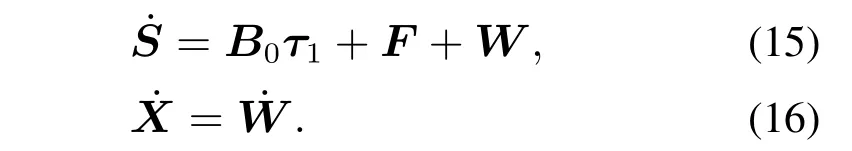
根据假设1和假设2可知,总扰动的各分量及其变化率是有界的,记‖‖≤δ,δ为正常数.

常规ST算法可以削弱滑模控制的抖振问题,但不能完全移除抖振问题[16].本文引入光滑的双曲正切函数,并结合观测器状态估计误差的分数幂,改进常规的ST算法,移除常规ST算法的抖振问题,基于此,构造如下新的ST扩张状态观测器:

定理1针对增广系统(15)-(16),在假设1和假设2下,通过适当选取设计参数λ1>0、正的设计参数λ2和λ3满足式(29)和式(30),所构造的新的ST扩张状态观测器状态估计误差和(i=1,2,3)能够在有限时间内收敛到零,可实现AUV不确定动态和未知海洋环境扰动引起的总扰动的有限时间实时估计.

3.3 ST控制律设计

设计如下新的ST控制律:

定理2考虑由系统(4)-(5)、ST扩张状态观测器(17)-(18)和ST控制律(33)-(34)构成的AUV三维轨迹跟踪闭环控制系统,在假设1和假设2下,通过适当选取正的设计参数λ1,λ2,λ3,λ4和λ5满足式(29)-(30)(47)-(48)(51),AUV 的三维轨迹跟踪误差ei(i=1,2,3)可满足式(7)和式(8)所描述的预设性能,且能够在有限时间Tc内收敛到零.

注3针对单输入单输出系统,文献[20-22]设计了常规ST扩张状态观测器及常规ST控制律,在那里,系统稳定性分析依赖于“观测器状态估计误差的绝对值小于跟踪误差绝对值的平方根”这一假设条件;而本文所提出的新的ST扩张状态观测器以及新的ST控制律的设计方法是针对多输入多输出系统的,更具有一般性,且通过选取恰当的李雅普诺夫函数(37),系统的稳定性分析不依赖于上述严格假设.

4 仿真验证

这部分以一艘AUV为例进行仿真,其运动数学模型参数[8]如下:

4.1 所设计控制律的性能

为了验证本文所设计控制律的有效性,下面在两种情况下对所设计控制律进行仿真实验.

情况1海洋环境扰动选取为

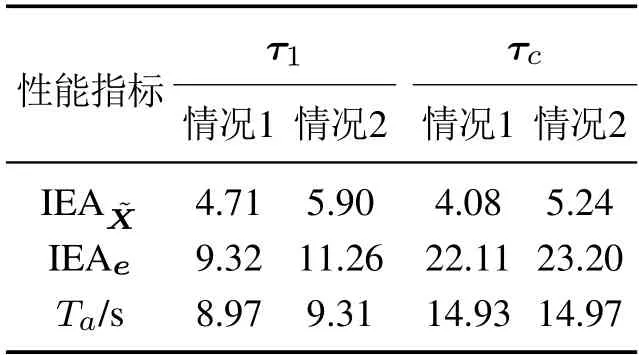
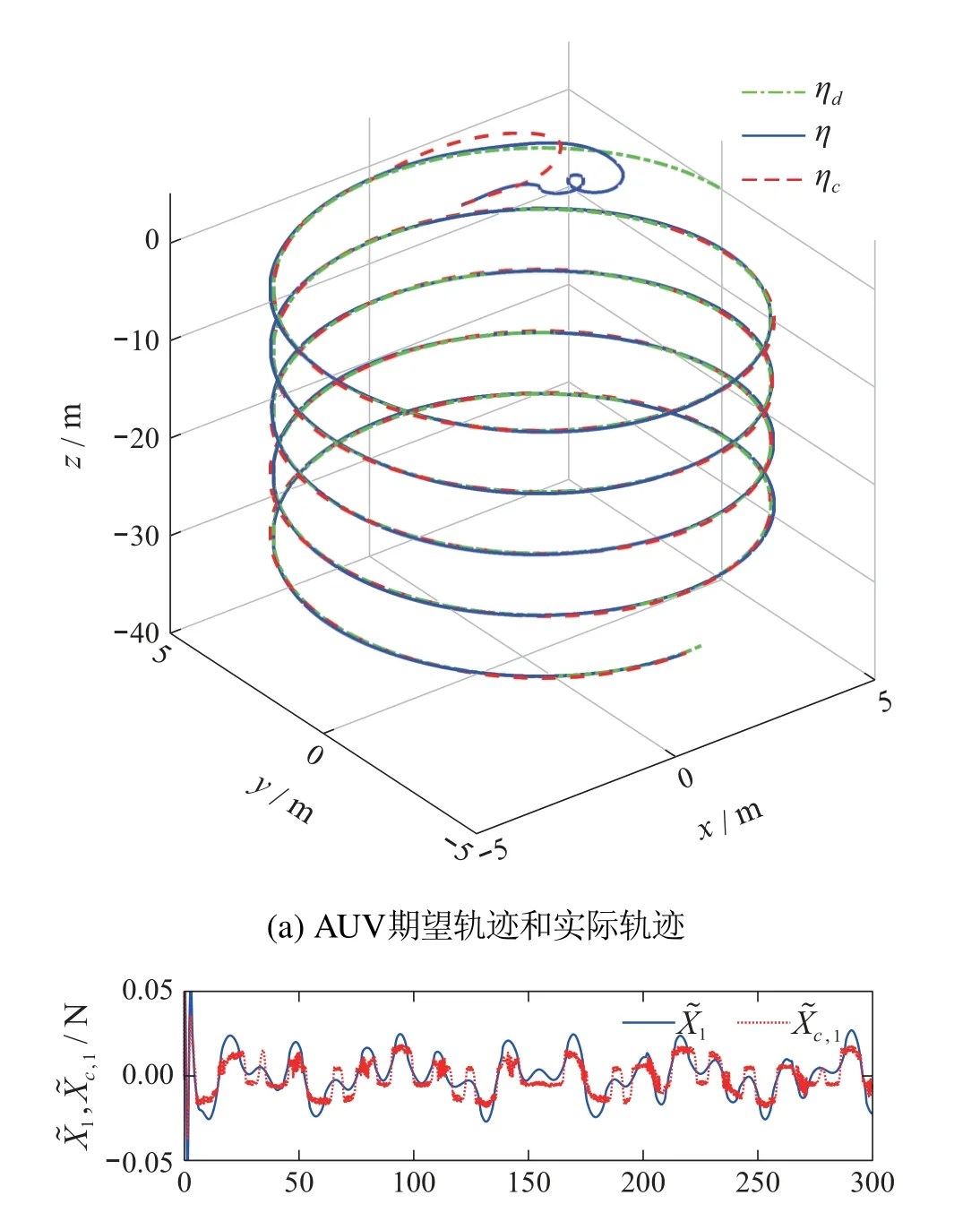
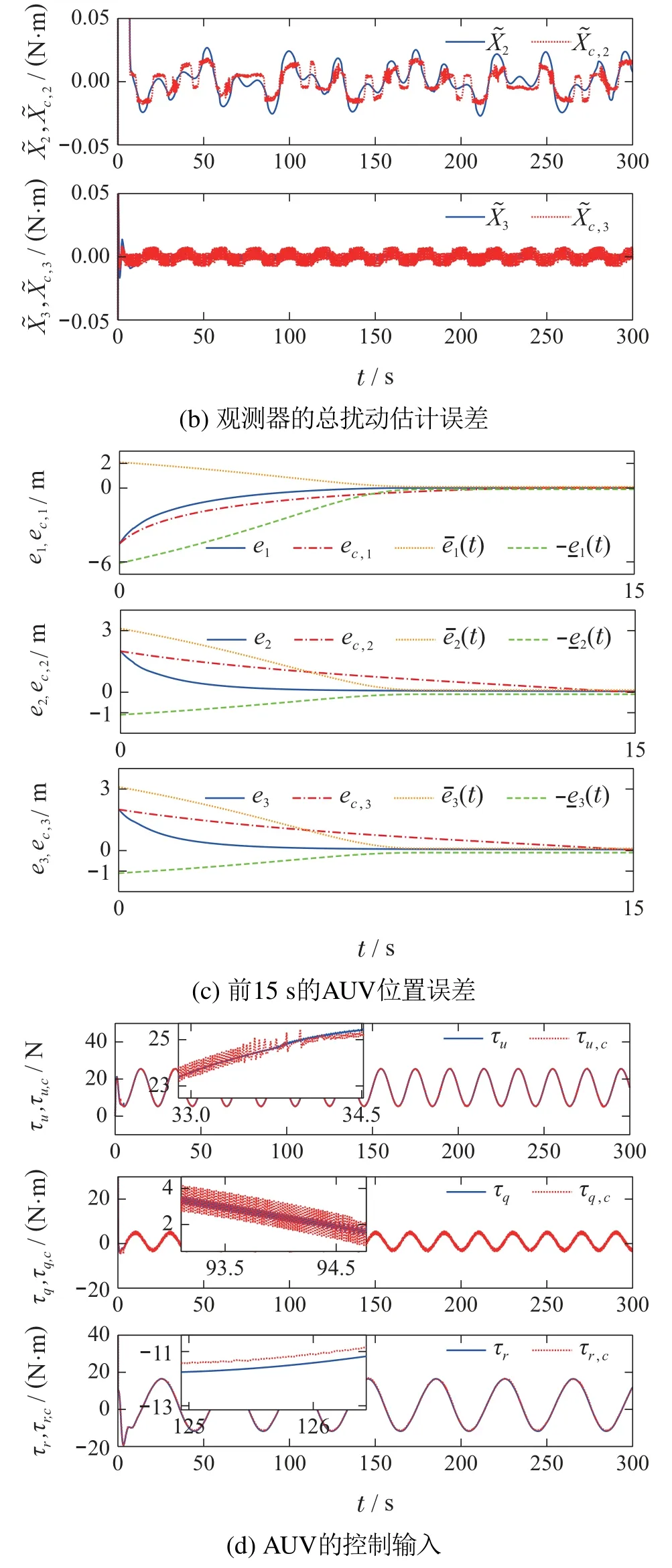
由图3(a)可见,AUV的实际运动轨迹能够跟踪期望的轨迹;图3(b)和表1中的性能指标IEA表明所构造的ST扩张状态观测器能够实时估计AUV不确定动态和未知时变海洋环境扰动构成的总扰动,正如定理1所述;图3(c)和表1中的性能指标IEAe和Ta表明,AUV轨迹跟踪误差e在Ta=8.95 s

图3 情况1下的仿真结果Fig.3 Simulation results in case 1

情况2AUV 惯性矩阵摄动ΔM=+30%·Mnom,海洋环境扰动增大为

AUV的期望轨迹、初始状态以及设计参数均与情况1的相同,这意味着所设计的控制律在参数摄动和扰动增大情况下保持不变.仿真结果用实线画在图4中,控制性能指标总结在表1中,可见,本文所设计的控制律展现了与情况1同样令人满意的控制效果,表明其对AUV存在的不确定动态和未知海洋环境扰动具有良好的鲁棒性.

表1 τ1和τc在两种情况下的性能指标Table 1 Performance indices of τ1 and τc in two cases

图4 情况2下的仿真结果Fig.4 Simulation results in case 2

4.2 仿真比较

为了验证本文所提出控制律的优越性,本小节将其与如下常规有限时间预设性能控制律进行仿真比较:

式中所有符号的含义均与所提出的控制律中符号的含义相同,下标“c”代表“被比较的”.

在第4.1节中的两种情况下进行仿真,仿真中AUV的期望轨迹、初始状态以及设计参数也均与第4.1节中的相同.仿真结果用虚线画在图3-4中,控制性能指标总结在表1中.图3(a)-(b)、图4(a)-(b)和表1中的性能指标IEAe和Ta表明,AUV的实际轨迹能够跟踪期望的轨迹,但是τc不能像本文所提出的控制律τ1那样保证AUV轨迹跟踪误差在10 s内收敛到稳态误差带,本文所提出的控制律τ1具有更好的瞬态控制性能;另一方面,从图3(b)、(d)和图4(b)、(d)可见,和τc均存在抖振现象,而及τ1均没有抖振现象.

5 结论

本文提出新型预设性能函数,可根据系统的性能要求、能力和限制条件,预先设置AUV轨迹跟踪误差进入并不再超出预设的稳态误差带所需的期望时间,提高了系统的响应速度,并提出了新的去抖振ST算法.基于上述,设计了新的ST扩张状态观测器和欠驱动AUV三维轨迹跟踪ST控制律,实现了具有不确定动态和未知时变海洋环境扰动的欠驱动AUV三维轨迹跟踪有限时间控制,同时保证AUV轨迹跟踪控制满足预设的瞬态和稳态性能.本文所提出的跟踪控制策略能够推广应用于诸如飞行器、无人车等一大类多输入多输出不确定非线性系统的轨迹跟踪有限时间预设性能控制.