基于机器视觉的化纤长丝断头检测算法

陈思俊， 陈振中

(东华大学 机械工程学院， 上海 201620)

为方便化纤长丝的运输和存储，工业生产通常将其卷绕成化纤丝饼。单股长丝由多根长丝组成，卷绕时纺丝容易发生断裂，形成化纤长丝断头，导致长丝质量下降。因此，化纤长丝断头检测和分类成为化纤企业质量检测的重要环节。目前，化纤长丝的生产线上主要还是依靠人工进行断头检测，检测效率和准确率都有待提高。因此，研究和设计化纤长丝断头自动化检测系统对化纤企业高效且高质量地生产长丝具有重要意义。化纤长丝断头传统的自动化检测方式主要有电磁感应、光电传感和热敏传感等方式。吕汉明等[1]提出一种基于声音检测与分析的细纱断头检测方法，根据纺纱声音信号波峰分布的均匀程度判断是否存在纱线断头。李强等[2]通过比较光电传感器探测到的纱线经过探头时的方波信号，判断是否存在纱线断头。李效东等[3]设计了一种基于红外传感器的纱线断头检测装置，通过比较运动探头经过纱线处的光信号差异，判断是否存在纱线断头。上述装置在检测完全断开的普通纱线时效果明显，但无法对具有局部断头特性的化纤长丝进行有效断头信息采集和分析，这正是化纤长丝断头检测的难点所在。近年来，日臻成熟的机器学习和图像处理算法为机器视觉技术在长丝断头检测领域的使用提供了理论支持。相比较传统检测方法，机器视觉断头检测方式[4]可以很好地解决断头信息难以采集的问题，但难点在于缺乏专用的化纤长丝断头检测算法。

工业生产中将化纤长丝规格用总线密度和纺丝根数组合表征。其中，将无断裂纺丝、断裂纺丝占比少于1/3、断裂纺丝占比超过1/3的长丝分别标记为无断头、轻微断头和严重断头。为满足自动化巡检的生产需求，并解决传统机械式断头检测方式无法准确检测和分类化纤长丝断头问题，本文在现有纱线断头检测研究的基础上，设计了一套基于机器视觉的化纤长丝断头检测系统。该系统继承了传统的巡回式步进小车检测平台，配套开发了一种专用的基于霍夫变换和径向基函数神经网络的化纤长丝断头检测和分类算法。该算法首先对获得的长丝图像进行小波去噪和阈值分割处理；然后通过霍夫变换将二值化的长丝图像进行主干和断头形状分割；最后提取分割后图像的几何特征，并基于径向基函数神经网络进行训练和预测，实现对化纤长丝断头的检测和分类。

1 检测装置构建与图像采集

熔体直纺工艺[5]主要包括化纤聚合物熔融、计量泵喷丝成形、侧风冷却和长丝卷绕等流程。化纤长丝在卷绕过程中由于受到载荷分布不均匀等因素的影响，易在集束挂钩处形成长丝局部断头。为实现长丝图像的有效采集，本文设计了一套专用的化纤长丝断头检测装置，如图1所示。该装置包括一部带镜头的工业相机和一台步进式巡回小车。工业相机通过千兆网口与小车内主机相连，小车接收脉冲信号步进移动，相机正对易发生断丝区域的长丝进行图像采集。

注：1-导轨；2-断丝区域；3-挂钩；4-喷丝板；5-箱体；6-计量泵；7-注料口；8-长丝断头；9-摄像头；10-步进式巡回小车；11-主机。

工业相机镜头选型是视觉检测系统设计的一个重要环节，图2所示的相机视场图较详细地描述了镜头的工作原理。根据图2可知，镜头焦距的计算公式如式(1)所示。

图2 相机视场图

(1)

式中：f为工业镜头的焦距;W为实际检测中工作距离;S为相机的靶面尺寸的宽度;F为视场的宽度。

根据现实工作环境确定工作距离为500 mm，视场宽度为400 mm。根据式(1)计算焦距并选取合适镜头。所选M0814-MP2型工业镜头的具体参数如表1所示。

表1 工业镜头参数

待测对象为16.67 tex/36 f规格的POY(pre-oriented yarn)系列长丝，纺丝速度为2 000 m/min。运用图2中的图像采集装置采集1 500张250像素×400像素的长丝图片，其中无断头、轻微断头和严重断头图像各500张。采集所得的3类化纤长丝图像如图3所示。

图3 采集的化纤长丝图像

2 长丝的图像分割与形状特征提取

2.1 长丝图像分割

长丝图像分割阶段分为图像去噪、阈值分割[6]和形状分割3个部分。本文图像去噪选用小波软阈值去噪方式，其可以平滑图像噪点。将阈值分割算法改进为基于像素变化梯度的阈值分割，以对图像进行阈值分割，生成二值图像。选用霍夫变换对图像直线主干进行提取，以实现长丝主干和断头部分分割。

2.1.1 小波阈值去噪

由于生产车间的嘈杂湿热环境和背景杂质的影响，CMOS相机获取图片时会出现大量噪点。过多的噪点会影响后期图像处理和提取特征，导致长丝断头识别率偏低。为消除噪声点对特征提取带来的影响，需要对图像进行平滑去噪。

小波阈值去噪[7-9]是一种基于小波变换的频率域图像去噪算法，二维连续小波函数如式(2)所示。

(2)

式中：α为窗口伸缩尺度；τ为平移量；f(ti)为时域信号函数。窗口伸缩尺度α控制小波的频率，起控制小波伸缩的作用，平移量τ用来平移小波，起遍历扫描小波的作用。

本试验采用Symlet[10]小波系列中的sym5小波，假设加性噪声污染后的图像信号S(t)如式(3)所示。

S(t)=f(t)+εe(t)

(3)

式中：f(t)为图像原始信号;e(t)为噪声;ε为噪声系数的标准偏差。

原始信号f(t)的小波系数ωi,t较大，主要表示原始图像中比较重要的信息和奇变位置；而e(t)在每一级的尺度分解上的小波系数ωi,t都相对较小，分布也较为相似，可以通过选定适当的阈值θ进行阈值去噪。硬阈值去噪函数存在不连续性问题，会导致去噪重构后的图像产生局部震荡现象。而软阈值去噪函数变换是连续的，在去噪的同时可以解决震荡问题，因此采用软阈值去噪方式，如式(4)所示。

(4)

式中：sgn为符号函数；ωi,t中下标i为小波层数，t为时间，当ωi,t值大于零时，取正值，反之则取负值。

2.1.2 基于像素变化梯度的阈值分割

生产现场中所拍摄的图像质量受环境、光照等影响显著，为降低光照等外界因素对后期特征提取的影响,采用阈值分割算法对图像进行二值化处理。每幅图对应的像素变化梯度因光照和图像内容不同而存在差异，但由于长丝像素点数占整体比例较小以及长丝像素值高于背景像素值这两个共性特点，因此长丝图像像素变化梯度图呈现相似的变化趋势。

通过分析像素变化梯度图发现，在长丝主干对应的像素值左侧会出现像素点突变，图中表现为1个或多个突出波峰，之后像素梯度趋于平缓，将波峰之后趋于平缓处的像素值作为图像分割的阈值T。在M像素×N像素大小的二值图像中，用f(i,j)表示第i行j列图像对应的像素值。i取1～M所有整数点，j取遍1～N所有整数点，遍历图像中每个像素点，通过式(5)求得f′(i,j)为阈值分割后的二值图像。

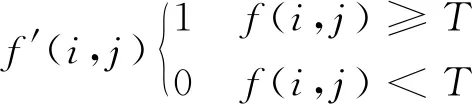
(5)

2.1.3 霍夫变换形状分割

霍夫变换主要利用极坐标进行直线标定。根据文献[11]可知，在二维空间中，直线可以用极坐标下的公式ρ=xcosθ+ysinθ表示,其中，ρ表示该直线到原点的垂直距离，θ表示x轴到该直线之间的夹角，取值为-90°～90°。若两点共线，则对应的直线具有相同的ρ和θ，此时的ρ和θ即本文选取的在线的极坐标参数。直角坐标系中共线的两点(xi，yi)和(xj，yj)被映射到极坐标参数空间时表现为两条正弦曲线，曲线交点即本文所要求的(ρ0，θ0)。

在M像素×N像素大小的二值图像中，用f(x，y)表示第x行y列图像对应的像素值。x取1～M所有整数点，y取1～N所有整数点，遍历图像中每个像素点，若f(x，y)值不为0，则通过式(6)求得对应坐标下的ρ和θ值。

(6)

在参数空间建立一个二维数组累加器，并将获取的ρ和θ值取整后作为横纵坐标，在累加器对应的该坐标位置中进行累加操作，最终得到最大累加器所对应的(ρ，θ)值，即共线点最多的直线所对应的ρ和θ。由于长丝主干为贯穿于图像整体的直线，在霍夫变换空间中，找出最大值对应的ρ和θ即长丝主干所对应的直线参数。通过将原图像二值图像与长丝主干二值图像相减可以得到长丝断头二值图像。再运用特征提取算法，分别对无断头、轻微断头和严重断头3种长丝二值图像进行特征提取。

2.2 长丝形状特征提取

经特征提取后采集到的样本按4∶1比例随机分为训练集和测试集两部分，通过训练集训练优化径向神经网络模型，最终运用测试集对模型准确率进行检测。

对图像处理阶段生成的3种二值图像进行特征提取。提取的特征主要包含长丝原图像质心(x1,y1)；原图像面积S1以及周长C1；长丝主干质心(x2,y2)，主干面积S2和主干周长C2；长丝断头图像的面积Sd与周长Cd。通过式(7)对这些特征进行计算，将计算结果作为径向神经网络输入层输入。

(7)

式中：质心距D为长丝主干质心和原图像质心之间的距离；面积比Sp为原图像面积和主干面积比值；周长比Cp为原图像周长和主干周长比值；断头面积周长比Pd为提取的断头部分面积和周长的比值。

3 断头识别分类

径向基函数是一个取值只取决于距原点距离的实值函数，即Ø(x)=Ø(‖x‖)，亦或是到某一点c的欧氏距离，即Ø(x,c)=Ø(‖x-c‖)。任意满足该特性的函数被称为径向基函数，常见的径向基函数主要为高斯核函数。

RBF(radial basis function)神经网络[12]是一种以径向基函数为激活函数的3层规模的前向神经网络。该神经网络在输入层与隐含层之间是非线性变换的，在隐含层和输出层之间是线性变换的，输出层包含3种识别特征权重值。RBF神经网络在分类能力和学习速度等方面优势明显。另外，由于RBF神经网络结构简单，能够逼近任意非线性函数且能够克服局部极小值问题，其在分类问题中得到广泛应用，本文基于该网络模型进行长丝断头分类。RBF神经网络模型如图4所示。

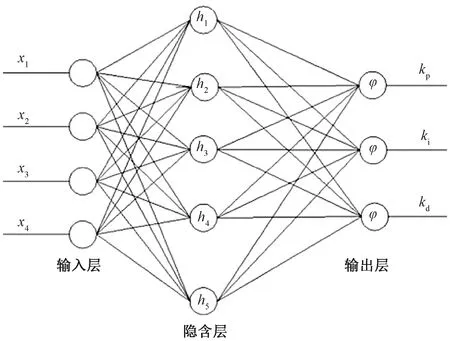
图4 径向基函数神经网络结构图

神经网络的识别特征权重预测值kp、ki、kd计算如式(8)所示。

(8)

式中：wp=[wp1,wp2,…,wp5]T,wi=[wi1,wi2,…,wi5]T,wd=[wd1,wd2,…,wd5]T为RBF神经网络的权重矢量；H=[h1,h2,…,h5]T为RBF神经网络的径向基矢量；φ为线性激活函数；hj为高斯核函数;q为隐含层的节点数。

式(9)为高斯核函数表达式。

(9)

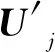
损失函数[13]模型为

L(k,k′)=-k(lnk′+(1-k)ln(1-k′))

(10)

式中：L(k,k′)为损失函数;k为测试集标签值;k′为预测值。

输入特征为一个具有4个维度的特征向量，通过径向基函数激活函数映射到高维空间的隐含层，再通过线性激活函数函数变换到输出层。隐含层节点个数为中心点的个数，本文以RBF神经网络为函数模型，其中输入层是由质心距D、面积比Sp、周长比Cp和断头面积周长比Pd组成的形状特征向量，通过优化隐含层节点数实现最佳分类效果，具体步骤如下：

(1)以隐含层节点数为自变量，通过无监督的聚类[14]算法求出每个节点的具体坐标值。

(2)初始化权重矢量，代入训练集数据，通过式(8)和(9)计算初始预测值，代入式(10)建立损失函数模型。

(3)通过梯度下降法[15]计算最小损失量下对应的权重矢量值，构建RBF神经网络模型，代入测试集，得出预测准确率。

(4)分析比较得出最佳隐含层节点数作为最终的预测模型隐含层节点数。

4 数据分析讨论

为验证本文系统算法的可行性，使用Intel Core i7-10750 H CPU，Win 10操作系统下的工控机作为硬件平台，基于MATLAB R2018b软件平台进行算法运算和参数分析。

4.1 小波层数及阈值选择

在确定不同层数下各阈值对应的小波系数后，基于这些小波涵数对图像进行去噪处理，分别计算原图像和去噪后图像的峰值信噪比(peak signal to noise ratio, PSNR),如图5所示。

由图5可知：当阈值不变时，随着小波层数的不断增加，峰值信噪比整体呈先上升后下降的趋势；当小波层数固定时，峰值信噪比呈先上升后下降的趋势。当小波层数取6、阈值取45时，图像峰值信噪比达到最大，去噪效果达到最佳。

图5 小波层数和阈值与峰值信噪比的关系

4.2 基于像素变化梯度的阈值选择

不同断头灰度图像的灰度分布如图6所示。由图6可知，受到光照和断头严重程度等因素的影响，各图像的灰度分布图差异明显，但由于长丝像素点数占整体比例较小以及长丝像素值高于背景像素值，各图像像素变化梯度图呈现相似的变化趋势。图6中主要表现为1个或多个突出波峰的存在，并且会在某一阈值后趋于平缓。

图6 不同断头长丝灰度分布图

阈值选取对无断头、轻微断头、严重断头长丝图像分割效果的影响如图7～9所示。

图7 无断头长丝图像阈值选取对图像分割效果影响

图8 轻微断头长丝图像阈值选取对图像分割效果影响

图9 严重断头长丝图像阈值选取对图像分割效果影响

结合图6发现:当阈值取在波峰或波峰之前时，图像会产生许多瑕点，不利于下面的特征提取；当阈值取刚趋于平缓后的值时,去背景效果达到最佳；当阈值继续往后取时，图像明显失真。因此寻找灰度变化峰值右侧附近段值作为阈值,可以很好地实现长丝与背景的分离。

4.3 霍夫变换参数分析

长丝图像霍夫变换空间图如图10所示。由图10可知，霍夫变换空间图中各点的像素值表示极坐标取值在对应ρ和θ坐标位置的点出现个数，数值越大表明共线的点越多，由于主干是一条贯穿于整个图片的直线，可以通过寻找最大值找到主干所对应的直线区域。图10中红框标记点的颜色最深，表示该点对应的数值最大，其对应的ρ和θ即为长丝主干所在直线极坐标参数。

图10 长丝图像霍夫变换空间图

表2为部分图像的ρ和θ信息。由于长丝主干多为竖直方向，因此θ数值在0左右徘徊，将相应的ρ和θ值代入公式ρ=xcosθ+ysinθ可求出主干所在直线全部坐标，以此提取出图像主干。

表2 部分图像主干的ρ和θ值

4.4 长丝图像处理效果图

严重断头图像处理后的效果如图11所示。长丝原图像经过小波软阈值去噪后效果如图11(b)所示，可以看出去噪后长丝背景变得平滑；图11(b)经阈值分割后的效果如图11(c)所示，可见长丝与背景分割效果明显；图11(c)经霍夫变换后提取的长丝主干如图11(d)所示，图11(c)与(d)相减得到的长丝断头如图11(e)所示，可见图11(d)～(e)很好地保留了长丝的形状特征。

图11 严重断头长丝图像处理效果图

4.5 RBF神经网络优化与预测

采集的部分长丝图像形状特征数据如表3所示。将表3中数据归一化处理后代入RBF神经网络模型进行训练。

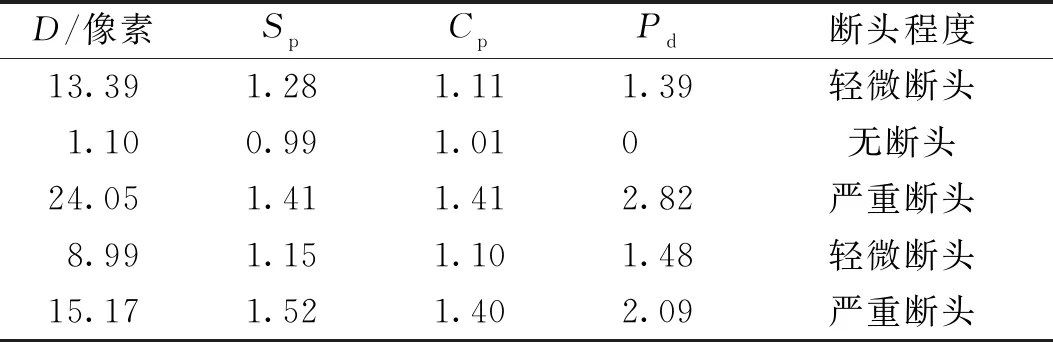
表3 化纤长丝形状特征值及对应的断头程度

RBF神经网络隐含层节点数与均方误差关系图如图12所示。由图12可知，当RBF神经网络隐含层节点数达到780后，均方误差趋于平缓，表明模型已经与训练集达到很好的匹配效果，充分使用每一个训练集。

图12 RBF神经网络隐含层节点数与均方误差关系图

RBF神经网络隐含层节点数与预测准确率关系如图13所示。由图13可知，当RBF神经网络隐含层节点数在720左右时,预测准确率达到最高值95%以上，选择720作为RBF神经网络隐含层节数可以达到最佳效果。

图13 RBF神经网络隐含层节点数与预测准确率关系图

4.6 化纤长丝断头识别算法效率与稳定性

人工检测并判断每根断头平均时间在1 s以上，随着检测时间变长，工人很容易出现误判。基于机器视觉进行断头分类主要包含图像处理、特征提取和断头识别。由于每张图片处理时间较短，故统计300张测试集图片各阶段的处理时间，取平均值作为每张图片的各部分平均处理时间，统计结果如表4所示。由表4可知，长丝图像处理阶段小波去噪、阈值分割和形状分割以及特征提取阶段平均处理时间均在10-2s数量级上，测试集300张图像断头识别总时间在10-1s数量级上，相比人工检测，达到了快速识别的目标。

表4 各阶段处理时间

为验证化纤长丝断头识别算法的稳定性和高效性，后续在现场采集了具有相同数量训练集和测试集的10组样本进行试验，结果如图14所示。由图14可知，每组数据的测试准确率为94%～100%，表明该算法具有一定的稳定性和高效性。

图14 10组样本分类结果

5 结 语

基于霍夫变换和RBF神经网络设计了一套化纤长丝断头检测系统。借助设计的检测装置对150 tex/36 f规格的POY长丝3种不同程度的断头进行图像采集，并利用sym5小波去噪和改进的阈值分割算法对采集到的图像进行增强处理，通过霍夫变换对长丝进行主干和断头形状分割，将提取的长丝主干和断头主要形状特征导入训练好的RBF神经网络模型进行断头检测识别。试验结果显示，测试集300张图像平均图像处理时间在10-2s数量级上，断头识别总时间在10-1s数量级上，断头识别率可达95%以上。表明该系统可以快速去除图像背景噪点，实现长丝主干和断头形状分割，高效识别和分类化纤长丝断头，可为将来实现化纤长丝断头自动检测提供理论参考。