多次喷射柴油机实时预测模型参数映射关系辨识

胡 松，王贺春，王银燕，张金羽，杨福源

(1. 清华大学 汽车安全与节能国家重点实验室，北京 100084； 2. 哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001)

节能和减排是当代发动机领域面临的两大挑 战[1-3]．为了实现发动机的节能减排，许多先进的技术被提出并应用在发动机领域，导致先进发动机通常以复杂的控制策略和大量的控制变量为特征[4]．随着当代发动机电子控制单元(ECU)计算能力的快速增加，实现复杂的控制和算法成为可能．柴油机排放特性与缸内燃烧过程十分相关[5-6]，通过对EGR率、喷油压力、喷油始点、喷油次数、喷油量和进气压力等柴油机运行参数进行协同控制，可以实现排放和燃油消耗率的优化控制，而建立实时预测模型实现对排放和燃油消耗率在线优化控制是实现节能减排的重要前提．多次喷射发动机因其可兼顾排放和油耗特性，已成为未来发展的必然趋势，因而很多学者将精力投入到多次喷射发动机实时预测模型的研究中[7-8]．

发动机实时预测模型可分为发动机零维(0-D)物理模型和直接模型，其中0-D物理模型具有良好的预测能力，物理含义丰富且建模所需数据较少．常见的用于0-D物理模型的燃烧建模方法主要有基于燃烧规则的方法、基于现象学的方法和累积燃油质量方法，其中累积燃油质量方法最适合用于多次喷射发动机燃烧建模[7-10]．在基于累积燃油质量方法的发动机0-D物理模型理论框架及其校准方法研究中，Finesso等[7-9]和Catania等[10]已成功将其应用在多种型号的多次喷射发动机，但模型中待校准参数和发动机运行参数间映射关系辨识方法仍不明确．

对于参数间映射关系的辨识，比较传统的方法有响应面、Map图插值和经验公式(EF)等，普遍应用于发动机仿真、优化和控制领域[11-12]．但是随着越来越多的新技术被应用在发动机上，发动机系统已成为多输入、多输出的复杂系统，输入参数对输出参数的影响机理较为复杂，使得响应面和Map图插值方法难以实现[13]．EF方法通常需要选择或提出合适的函数结构和形式才能实现较高精度的辨识[13]．由于选择或提出合适的函数结构和形式比较困难，且具有很大的人为偶然性和随机性，因而此方法比较耗费人力．但因其对数据量要求很少，计算耗时极短，满足实时性要求，仍常见于一些研究中[9]．

近些年支持向量机、遗传算法和人工神经网络(ANN)等人工智能算法在各个研究领域都发展十分迅速，其中ANN具有高效、强适应性及高稳定性，已成为相对较为强大的候选算法之一[14]．但是ANN对数据量要求较多，且对数据误差比较敏感．尽管ANN已经在发动机领域得到了广泛的应用，但是当ANN用于面向控制的发动机模型，尤其是物理模型中的参数间映射关系辨识时，辨识效果和所建立的模型在稳态工况、瞬态工况的预测精度和计算耗时等性能指标是否满足实时性控制要求方面仍有待验证．此外，对EF和ANN两种方法在发动机预测模型参数映射关系辨识的应用也鲜见报道．

笔者基于前期关于多次喷射柴油机实时预测模型的研究基础，分别采用EF和ANN两种方法辨识输入/输出参数之间的映射关系，最终建立基于EF和基于ANN的多次喷射柴油机实时仿真模型，并在稳态和瞬态工况对两种模型进行预测性能对比，在快速原型设备上进行计算耗时对比．

1 多次喷射柴油机试验台架及测试工况

研究对象为菲亚特汽车公司(FIAT)生产的四冲程、水冷、高压共轨、多次喷射3.0L欧Ⅵ柴油机，配有VGT和高压EGR系统，其主要技术参数如表1所示，所采用的主要测试仪器及测试方法参见文献[4]，主要测试仪器的技术参数如表2所示．试验台架布置及详细描述参见文献[4]．研究共进行了410个重载车用发动机瞬态测试循环(WHTC)范围内稳态测试工况点试验，包括3部分：试验1为整个柴油机Map图工况，包含了基本运行参数，共123个测试点；试验2为几个主要特定工况点下的EGR扫描(EGR-sweep)试验测试，共162个测试点；试验3为几个主要的特定工况点下进行主喷定时/喷油压力扫描(SOImain/pf—sweep)试验测试，共125个测试点．稳态测试工况点分布参见文献[4]．

表1 欧Ⅵ柴油机主要技术参数 Tab.1 Main specifications of Euro Ⅵ diesel engine

表2 测试仪器主要技术参数 Tab.2 Main technical specifications of test instruments

2 多次喷射柴油机燃烧过程仿真模型

笔者采用的多次喷射柴油机燃烧过程仿真模型框架[4]主要包括缸内放热率qch、传热损失Qht、燃油蒸发吸热qf,evap、最高燃烧压力(PFP)、燃烧指数(MFB50)和平均有效压力(BMEP)的仿真模型建模方法．模型的具体理论依据、搭建过程及模型框架参见文献[4，15]，笔者只对模型中变量进行简要描述．

Qht,glob为燃烧过程总的传热损失，KP为预喷燃烧对应的燃烧参数，τP、τM分别为预喷和主喷滞燃期，K1,M和K2,M为主喷燃烧对应的燃烧参数，pIVC为进气阀关闭(IVC)时的缸内压力，pint为进气歧管压力，Δpint为pIVC和pint之间的压差，从IVC到SOC以及膨胀冲程(从燃烧结束(EOC)到EVO)，缸内压力可以分别认为是具有不同多变指数的多变过程．m和m′分别为压缩和膨胀过程对应的多变指数，PMEP为泵气压力损失，FMEP为摩擦损失，n为柴油机转速，prail为共轨压力，SOIP和SOIM分别为预喷和主喷对应的喷射角度(以下止点后作为参考点)，qtot,P为预喷喷油量，qM为主喷喷油量，qtot为总喷油量，pint和Tint为进气管空气压力和温度，VEGR为EGR系统高压废气阀开度，ρSOI,P和ρSOI,M分别为预喷和主喷对应的缸内气体密度，TSOI,P和TSOI,M分别为预喷和主喷对应的缸内气体温度，ρSOC,P和ρSOC,M为预喷和主喷燃烧始点对应的缸内气体密度，TSOC,P和TSOC,M为预喷和主喷燃烧始点对应的缸内气体温度，ρint为进气密度．

3 基于经验公式的参数间映射关系辨识

表3为基于经验公式各因变量参数的拟合精度．图1为部分经验公式的拟合结果，其中，RMSE为均方根误差，RMSEr为相对均方根误差．为了得到高精度的面向控制的柴油机预测模型， 柴油机模型中所有需要辨识的参数均应该采用数学方法直接或间接地与柴油机运行参数相关联．胡松等[4]已将直接测量参数、衍生参数作为候选自变量，采用敏感度分析方法得出基于幂函数的经验公式，并分析幂函数的固有缺陷和一些参数的固有特性，对部分经验公式 进一步改善，最终得出基于经验公式的参数间映射关系．基于相同的数据，笔者拟采用ANN算法实现参数间映射关系的辨识．

表3 基于经验公式各因变量参数的拟合精度 Tab.3 Fitting precision of each dependent parameter in diesel engine model based EF-model

图1 基于经验公式的各因变量参数映射关系拟合结果 Fig.1 Fitting results of each parameter in diesel engine model based on EF

基于各因变量参数和对应的自变量参数集间的映射关系及其决定系数拟合精度R2[4]，得出各个因变量对应的自变量集及基于EF的拟合精度．

4 基于ANN的参数间映射关系辨识

获得ANN模型包括参数选择、训练和测试共3个步骤．输入/输出数据通常会进行归一化处理，使输入/输出数据转化到一个特定的变化范围；归一化处理后的输入/输出数据再随机分成训练、测试和(或)验证数据集．在ANN建立之前，首先需要确定输入/输出变量参数的选取、隐含层个数、隐含层节点数、激活函数和训练算法[14]等参数．Lawrence等[16]研究发现，规模太小的ANN会导致欠拟合(underfitting)，而规模太大的ANN却会引起过拟合(overfitting)．因而在数据给定的情况下，需确认一个合适规模的ANN．

确定了各个因变量参数的自变量集(表3)，笔者将沿用得出的各个因变量参数的自变量集．为便于对比EF和ANN的性能，笔者采用和第3节相同的数据和自变量集．

4.1 ANN结构、训练算法、转换函数和激励函数的确定

前馈(BP)神经网络是普遍应用的神经网络，包含一个输入层、若干隐含层和一个输出层．误差反馈训练算法trainbr是人们熟知的BP训练算法之一，此训练算法可训练得出相对精确的ANN[17-18]，并且对于复杂非线性、数据规模小或者数据噪声信号多的训练数据[19]，仍可训练得出相对好的ANN，但存在训练迭代次数较大的缺点．笔者选取的训练用数据规模(410个工况点数据)比较小，并且神经网络结构较为简单，因而训练迭代次数较大并不会导致训练用时 过长而不可接受．故采用前馈ANN、BP训练算法trainbr作为ANN的训练算法．

对于很多ANN，为了提高训练速度，输入数据通常先采用归一化函数进行处理，然后再传递给输入 层[20]．笔者采用mapminmax归一化处理函数[20]将所有输入数据变化范围转换至[-1，1]区间内．相似地，神经网络的输出也需要与输入层归一化函数对应的处理函数．输出数据处理函数用于将提供的目标矩阵进行转换，然后用于训练神经网络[20]．

ANN的输出由激励函数调整，激励函数有多种，其中logsig、tansig和purelin为发动机领域常见的3种激励函数，而前两种的应用更为普遍．Negnevitsky[21]研究发现，tansig相比logsig，其训练速度更快．另外，tansig输出数值在-1～1之间变化，而logsig输出数值在0～1之间变化，因而tansig相比logsig在数据分析上具有优势[14]．激活函数采用tansig函数，定义为

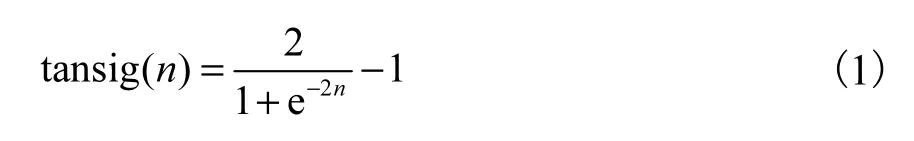
单层隐含层足以用于仿真发动机模型中的变量关系，并且已经在文献[22—24]中得到验证．因而隐含层个数选为1．

训练ANN过程中，将平均方差(MSE)作为损失函数，因为MSE具有良好的凸性、对称性和可微性，并且还是优化过程中很好的衡量指标[25]．ANN预测性能采用其输出结果和试验数据的回归分析进行评估[18]．笔者采用MSE和回归分析的决定系数R2衡量ANN的性能．ANN的建立及训练过程均在Matlab 2017b平台上进行．

4.2 ANN预测性能和隐含层节点数trade-off分析

ANN预测性能受神经节点数影响较大．过多的隐含层节点数会导致过拟合现象，而过少的隐含层节点数会导致神经网络结构过于简单，不能较好地捕捉到复杂系统的特性，即欠拟合现象[16]．因而隐含层节点数和ANN的预测性能之间存在折中关系．

所有稳态试验数据(共410个数据点)均用于生成ANN模型．其中80%的数据作为训练用数据，另外20%的数据作为测试数据，用于测试训练好的ANN的预测性能．对于训练用数据规模较小的情况，由于ANN的权值矩阵是随机生成的，因而训练结果存在一定的不确定性．可知，即使采用同样的训练数据训练得出的ANN，其预测性能也会存在明显不同．此外，对于每次训练过程，训练用数据和测试用数据是从所有试验数据中随机分配得出的，因而训练用数据和测试用数据也会发生变化．训练用数据和测试用数据的不同也会导致训练得出的ANN预测性能存在明显不同．只有当试验数据规模足够大时，训练得出的ANN预测性能的不确定性会很小[26]．

笔者对隐含层节点数Nh和ANN预测性能之间的trade-off关系进行研究，以在特定数据量的情况下获取最合适的ANN结构，避免过拟合和欠拟合．对于每个因变量，分别计算得出100次重复训练并测试的决定系数R2和MSE的平均值，笔者仅展示K1,M的trade-off分析结果及过程，如图2所示．可知ANN的100次训练平均误差随Nh的增加而减小，当Nh超过8之后，减小幅度较小；而测试误差先随Nh增加而减小，ANN处于欠拟合状态，当超过6之后，测试误差无明显变化甚至出现恶化，ANN处于过拟合状态．可知，对于K1,M，最佳Nh为6．同理，对于每个因变量，都存在一个最合适的Nh以使训练得预测性能良好的ANN可能性最大，从而确定各个因变量最适合的Nh，最终确定的Nh及对应的100次训练和测试精度(R2和MSE)平均值如表4所示．

表4 各因变量ANN隐含层节点数以及100次训练和测试精度平均值 Tab.4 Neuron number and corresponding precisions’mean value of 100 training trails for each dependent parameter

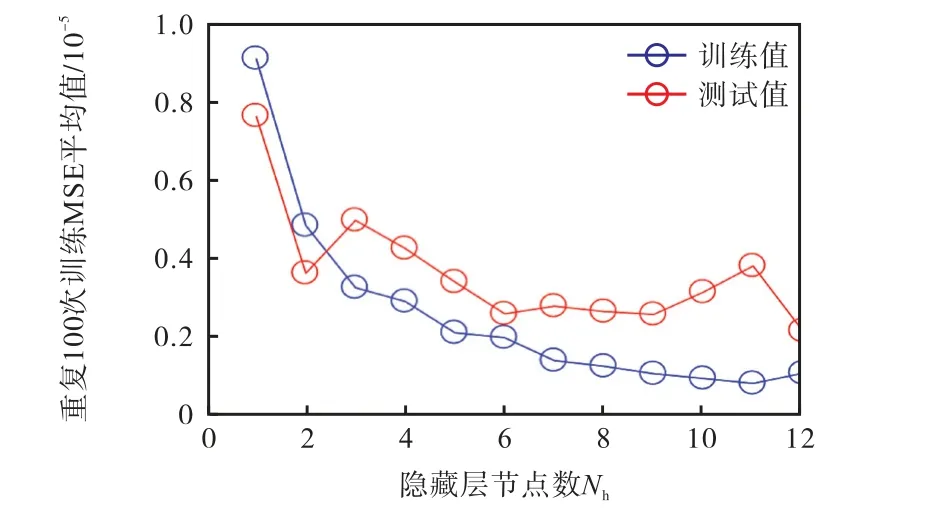
图2 K1,M ANN预测性能和隐含层节点数Nh的trade-off关系 Fig.2 Trade-off correlation between ANN predictive performance and hidden layer node number Nh for K1,M

由于ANN的训练用数据规模较小，训练得出的ANN精度存在一定随机性．为了训练得出一个预测性能相对较好的ANN，每个ANN均训练并测试了100次，并且每次训练均进行随机设定权值矩阵初始值，随机分配训练和测试用数据．为了从100次训练得出的ANN中自动筛选出预测性能较好的ANN，设计一个ANN自动筛选算法，如图3所示．

图3 重复100次训练最优ANN自动筛选算法 Fig.3 Automatic algorithm for selecting the best trained ANN from 100 training trails

自动筛选算法中：i为训练次数；N为最大训练次数；ANNb为该算法筛选出的最优ANN训练结果；ANN(i)为第i次训练得出的ANN；R2(i,1)、R2(i,2) 和R2(i,3)分别为训练、测试和整体数据(即训练和测试数据的整体数据)的R2精度；MSE(i,1)、MSE(i,2)和MSE(i,3)分别为训练、测试和整体数据的MSE精度；abs为绝对值函数．

最终，经过100次重复训练，并从中筛选得出各个因变量参数的最优ANN模型，训练值、测试值与试验值对比如图4所示，出于精简目的，此处只展示τP、τM、KP、K1,M和K2,M的对比结果．

图4 基于ANN的各因变量参数映射关系拟合结果 Fig.4 Fitting results of each parameter in diesel engine model based on ANN

对于各个因变量参数，其基于ANN的拟合精度和基于EF的拟合精度对比如表5所示．可知，ANN可以很好地拟合并预测各个因变量参数和对应自变量之间的关系，并且其拟合及预测精度均明显高于EF．表明ANN具有较好拟合柴油机模型中变量间关系的能力．和EF相比，采用ANN不用考虑函数的形式和结构问题，并且预测精度更好．

表5 ANN和经验公式拟合精度R2 Tab.5 Precision of ANN and empirical functions correlations

5 两种仿真模型预测性能及计算耗时对比

采用EF和ANN变量间映射关系，基于面向控制的多次喷射柴油机物理模型理论框架，分别建立基于EF的柴油机物理模型(EF模型)和基于ANN的柴油机物理模型(ANN模型)，笔者将针对两种模型的预测性能及计算耗时进行对比．

5.1 预测性能对比

对所建立的EF模型和ANN模型，分别在稳态工况和WHTC瞬态工况的预测性能进行了验证．图5和图6分别为EF模型和ANN模型在稳态工况和瞬态工况下的仿真结果．为便于直观表示MFB50滞后于发火上止点的曲轴转角位置，图5和图6中采用MFB 50-360表示．

由图5和图6可知，在稳态工况，对于MFB50、PFP和BMEP，基于EF模型的2R、RMSE和均方误差MSE预测精度分别为[R2＝0.975，RMSE＝0.631，MSE＝0.3980]、[R2＝0.995，RMSE＝1.820，MSE＝3.3100]和[R2＝0.999，RMSE＝0.153，MSE＝0.0233]；基于ANN模型的预测精度分别为[R2＝0.985，RMSE＝0.483，MSE＝0.2330]、[R2＝0.995，RMSE＝1.580，MSE＝2.5000]和[R2＝0.998，RMSE＝0.170，MSE＝0.0289]．在瞬态工况，对于MFB50、PFP和BMEP，EF模型的RMSE预测精度分别为1.2°CA、1.05MPa和0.07MPa；ANN模型的预测精度分别为1.2°CA、1.38MPa和0.08MPa．ANN模型在稳态工况的预测精度高于EF模型，但是在瞬态工况，其预测精度(尤其是PFP)出现明显恶化，低于EF模型．主要原因在于，模型中参数存在校准误差和不确定性，ANN相比EF具有更强的非线性拟合能力，可以实现更好的非线性拟合，但是对参数误差和不确定性更加敏感．对于模型参数来说，校准误差和不确定性较高，因而EF更适合用于模型中参数间映射关系的辨识．

图5 基于经验公式和基于ANN的柴油机物理模型稳态工况仿真结果对比 Fig.5 Comparison of simulation results of empirical functions and ANN physics-based in diesel engine model under steady-state work conditions

图6 基于经验公式和基于ANN的柴油机物理模型在WHTC瞬态工况仿真结果 Fig.6 Simulation results of empirical function and ANN physics-based diesel engine models under WHTC transient-state work condition

5.2 计算耗时对比

对于面向控制的柴油机模型，除了模型预测性能外，计算耗时也是衡量模型性能的一个重要指标．将EF模型和ANN模型两个模型分别载入ETAS ES910型快速原型及接口模块中进行测试运行．ETAS ES910技术参数如下所述：主处理器型号为NXP PowerQUICCTM Ⅲ MPC8548，800MHz双精度浮点型；RAM为512MByte DDR2-RAM (400MHz时频)；Flash为64MByte Flash；NVRAM为128kByte NVRAM．由测试可知，基于EF和基于ANN的柴油机物理模型计算耗时相当，均约为350µs，远低于实际柴油机单个循环所需时间(约为20ms)，能满足燃烧过程实时控制的要求．

6 结 论

(1) 相比基于幂函数的经验公式，ANN对柴油机物理模型中参数间的非线性映射关系辨识效果更好，但是对数据误差的敏感度较低．

(2) 相比基于EF的柴油机物理模型，笔者建立的基于ANN的柴油机物理模型在稳态工况对MFB50、PFP和BMEP的预测精度更好；在WHTC瞬态工况，对MFB50、PFP和BMEP预测精度出现明显恶化(尤其对于PFP)，预测性能较差；主要因为参数本身具有较大的校准误差和不确定性，而ANN模型，相比EF，对误差和不确定性更加敏感，EF相比ANN更适合用于辨识柴油机物理模型参数间映射关系．

(3) 所建立的基于EF的柴油机物理模型和基于ANN的柴油机物理模型，其在ETAS ES910快速原型设备上测试的计算耗时相当，约为350µs，远低于实际柴油机单个循环所需时间(约为20ms)，二者均能满足燃烧过程实时控制的要求．

致谢:

感谢FPT(FIAT Powertrain Technologies)为本研究提供的试验数据．感谢Stefano d’Ambrosio教授和Roberto Finesso教授在本研究过程中给予的指导．