基于参数自学习的柴油机转速主动抗扰控制

邵 灿，宋 康，陈 韬，谢 辉

(天津大学 内燃机燃烧学国家重点实验室，天津 300350)

柴油机具有灵活性高、使用方便快捷等优点，广泛应用于生产和生活中．其中，转速控制的平稳性是影响柴油机运行平顺性的关键，但在实际应用中面临诸多控制难题，制约了转速的控制品质，如外部突变负荷和随机负荷难以直接测量，使得传统控制算法只能根据转速控制误差被动调节，转速响应慢；从喷油量到燃烧做功，再到驱动转矩输出，这个过程复杂、非线性，导致传统控制策略需要标定大量Map[1]，工作量大；发动机存在老化变异现象，使得控制参数不再适应实际柴油机，影响了转速控制效果．

比例-积分-微分(PID)控制是产品柴油发动机中常用的控制方法，但PID控制器的工况适应范围有限，超出设计工况后控制效果变差[2]．因而在实际应用中通常需要PID控制器根据工况的变化进行参数优化，如PID参数自整定[3]．文献[4]最早将模糊控制应用于柴油机的转速控制中，获得了比传统PID更好的工况适应能力．Di等[5]将模糊控制理论应用于转速的PID控制，降低了转速控制中的超调量和调节时间，但模糊规则的设计比较复杂耗时．

除传统PID控制以外，学者们对自适应控制和基于模型的控制方法也进行了研究．Yildiz等[6]和Yin等[7]较早将自适应控制应用于转速控制中，改善了怠速工况的转速控制品质．Pavković等[8]提出一种基于自适应卡尔曼滤波的转速控制方法，降低了对噪声的敏感性，但在负荷突变过程的转速波动幅度仍然较大．Li等[9]设计了基于线性规划的模型预测转速控制器，Xu等[10]设计了一种非线性的模型预测控制器，结果表明：控制器在负荷转矩扰动和参数不确定的情况下，实现了良好的控制品质；同时，模型预测控制所需的计算量较大，在实时性要求较高的嵌入式环境下，毫秒级的控制过程实现困难．

基于此，笔者以目标运行转速为1500r/min的发电用柴油机为研究对象，并在满足转速控制偏差(7%)的行业标准基础上进一步优化控制效果，提出一种参数自学习主动抗扰控制算法．在传统转速控制模型中引入等变化率负荷转矩模型，采用扩张状态观测器[11](ESO)对其进行在线主动观测，并用于实时抑制转速波动；为不断改善控制品质、适应发动机特性变化，提出了模型参数的自学习算法；通过硬件在环(HIL)仿真平台和发动机台架试验平台对算法的抗干扰能力和自学习能力进行了测试和验证．

1 研究平台及面向控制的模型

1.1 台架试验平台

通过一台配备高压共轨燃油喷射系统的直列6缸、涡轮增压柴油机试验台架开展研究．图1为试验台架及数据采集方式示意．后处理包括柴油氧化催化器(DOC)、柴油颗粒捕集器(DPF)和选择性催化还原(SCR)3部分．表1为发动机主要技术参数．

图1 试验台架及数据采集方式示意 Fig.1 Schematic of test platform and data collection method

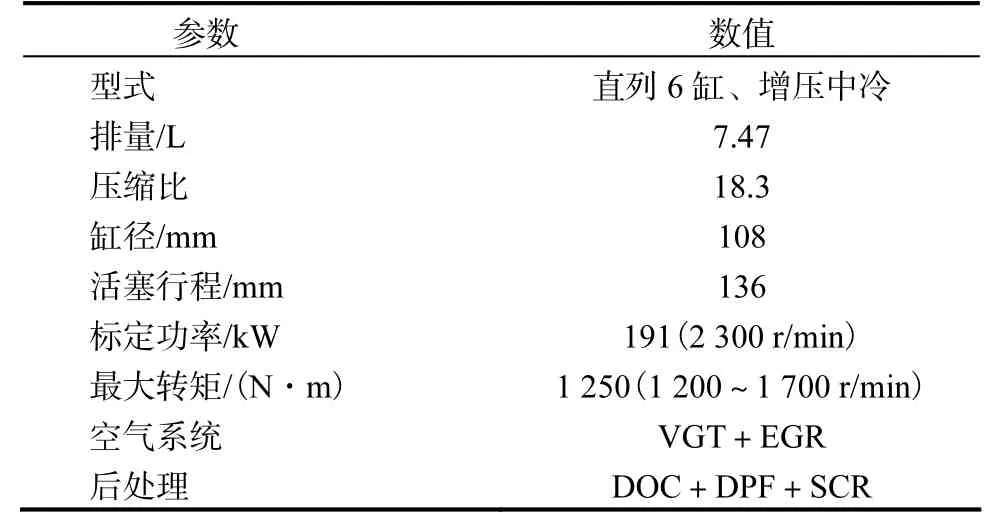
表1 发动机主要技术参数 Tab.1 Engine specifications

1.2 面向控制的模型

针对标定和负荷估计难的问题，开发了基于牛顿第二定律的曲轴转速动态模型[12]．主要包括指示热效率子模型、摩擦转矩子模型和负荷转矩，其中负荷转矩由扩张状态观测器观测得到，动态模型可表示为

式中：J为曲轴及刚性连接轴系的转动惯量；n为转速；Min、Mfric和Mload分别为平均指示转矩、摩擦转矩和负荷转矩．

1.2.1 指示热效率模型

平均指示转矩[13]可表示为

式中：ncyl为冲程系数；HLHV为柴油燃料低热值，取值为4.325×107J/kg；ηin为指示热效率；mf为单缸的循环供油量．

ηin随负荷和转速的改变而变化，经验模型为

式中：h1、h2和h3为转速项待标定参数；d1、d2和d3为循环供油量项待标定参数．

为得到指示热效率模型待标定参数，需利用试验数据对模型进行标定．以发动机台架试验热效率实测值为基准，使用全工况的数据对模型进行标定．采集不同转速、负荷下稳态工况时的指示热效率数据，同步采集转速和循环供油量稳态数据，得到119个稳态工况点标定数据，可确定模型参数．

采用非线性批量最小二乘方法对指示热效率模型进行离线参数辨识．最小二乘方法通过代价函数的迭代计算使模型的估计值与实际值差值的平方和最小，优化得到模型参数．优化函数为

式中：F(x,xdata)为数据x输入后计算的模型估计值；ydata为实际值．

表2为辨识得到指示热效率模型的参数，可适应不同运行工况下的指示热效率估计．

表2 指示热效率模型参数辨识结果 Tab.2 Parameter identification results of indicating thermal efficiency model

为验证辨识得到的指示热效率模型精度，将离线辨识得到的指示热效率模型参数值代入模型，计算与数据采集工况相同转速和循环供油量工况下模型输出的ηin模拟值，图2为ηin试验值与模拟值对比．

图2 不同负荷下指示热效率模型验证 Fig.2 Verification of indicating thermal efficiency model under different loads

可知，模拟值与试验值吻合度较高，模型估计偏差在6.3%以内．在高速、低负荷区和低速、高负荷区存在小范围的模型估计值偏差增大的情况．虽然模型在部分工况的误差较大，但是由于研究对象为发电用柴油机，其运行转速区间在1500r/min附近，而在转速为1500r/min的典型工作转速下，指示热效率模型估计值的相对偏差在4.5%以内．

1.2.2 摩擦转矩建模

摩擦转矩采用简化平均值模型[14]，即

式中：m1、m2和m3为转速项待标定模型参数．

与指示热效率模型类似，为得到摩擦转矩模型待标定参数，需要利用试验数据对模型进行标定．根据转速和负荷的不同，划分为119个工况点，利用倒拖工况，得到各工况点下稳态时的摩擦转矩，同步采集转速稳态数据，形成标定数据用于模型参数的确定．

同样，通过非线性批量最小二乘方法进行离线参数辨识，得到摩擦转矩模型的参数如表3所示．

表3 摩擦转矩模型参数辨识结果 Tab.3 Parameter identification results of friction torque model

为验证辨识得到的摩擦转矩模型的精度，将辨识得到的参数代入摩擦转矩模型中，得到不同转速下摩擦转矩的模拟值，与摩擦转矩试验值对比，如图3所示．可知，试验值与模拟值吻合度较高，摩擦转矩模型的相对偏差在7%以内．与指示热效率模型类似，摩擦转矩模型模拟值在负荷较低或高转速工况下有偏差明显增加的现象，在1500r/min左右的工作转速区，模型估计偏差较小(5%以内)．

图3 不同负荷下摩擦转矩模型验证 Fig.3 Verification of friction torque model under different loads

综上，根据数据驱动建模与经验建模相结合的方式得到摩擦转矩和指示热效率模型的表达式，曲轴转速动态模型可表示为

负荷转矩Mload通过笔者提出的观测方法得到．

2 控制算法设计

2.1 柴油机转速控制算法架构

针对柴油机负荷转矩不可测、不确定及发动机老

化变异的问题，提出的转速控制架构见图4．

图4 转速自学习主动抗扰控制算法架构示意 Fig.4 Architecture of the speed self-learning active disturbance rejection control

根据目标转速与实际转速之差，计算所需的惯性力矩Mintia；通过扩张状态观测器(ESO)的观测作用，补偿所估计的负荷转矩Mload后，得到所需的有效转矩Me；最后，经过摩擦转矩Mfric补偿，结合平均指示转矩反算得到所需要的循环供油量．转矩关系为

惯性力矩Mintia为转速变化的动态过程中，由曲轴轴系的旋转运动而产生的往复惯性力矩；有效转矩Me为发动机曲轴上可以输出的转矩值；负荷转矩由“负荷转矩主动观测”算法估算．

摩擦转矩模型参数和ηin在参数离线辨识的基础上，通过自学习算法在线更新．其中，摩擦转矩参数是在停机过程根据发动机转速和自身摩擦转矩的关系，运用递推最小二乘方法学习得到．ηin则是通过在发动机负荷和转速相对稳定时，利用喷油量和转速之间的动态关系，根据递推最小二乘方法学习得到．

2.2 主动抗扰控制算法

2.2.1 负荷转矩的主动观测算法

在曲轴转速动态模型中，负荷转矩是未知动态，无法进行精确建模．因而笔者运用主动抗扰控制思想，将负荷转矩等效为总扰动[15-16]的一部分，通过ESO进行在线观测，对负荷转矩进行控制补偿．

由于算法设计是针对负荷突变情况下的负荷转矩观测，可假设负荷转矩在加载初期变化率保持恒定，将式(6)改为带有负荷转矩的模型，即

式中C为假定未知常量．

式(9)中，负荷转矩未知，且摩擦转矩模型及指示转矩模型中具有估计偏差，将其影响统一视为“总扰动”这一扩张状态，得

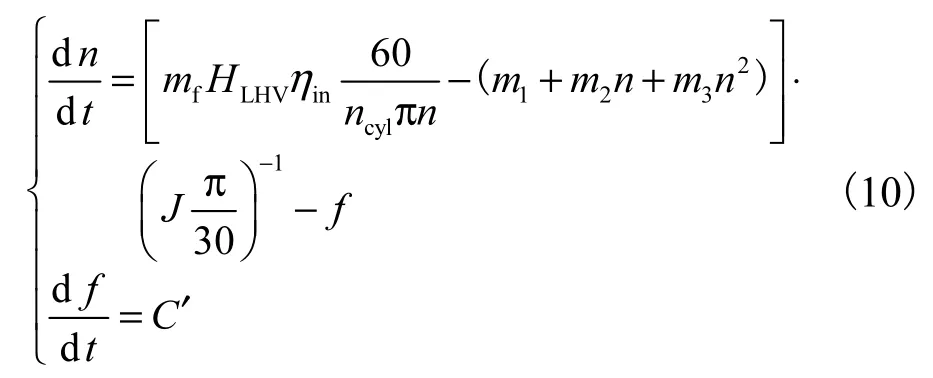
式中u为控制器循环供油量控制输出．

由于n可直接测量，因而设计针对式(11)的降阶扩张状态观测器[17](RESO)．可得总扰动测量值为

以总扰动和总扰动的二阶导数为状态量，得二阶RESO的表达式为

由于在总扰动的测量值表达式中存在转速的微分，而微分的处理极易使信号产生噪声，因而需对ESO做进一步处理，将转速的微分项消除．

定义两个新的状态量η、ξ，将其转化为扩张状态观测器的两个新的状态，分别表示为

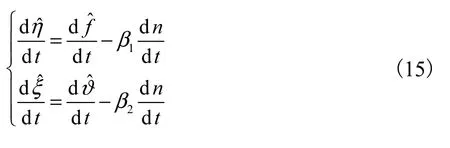
将式(12)～(14)代入式(15)，得

式中：ξ和η为降阶观测器状态量，是替换原状态量负荷转矩和负荷转矩变化率，以消除容易产生测量噪声的转速微分信号．

将式(16)整理成状态空间的形式，有

将ESO的极点配置在ωo−处[18]，则观测误差增益β1和β2为

式中ωo为观测器带宽．

2.2.2 主动抗扰控制律设计

针对式(11)，主动抗扰控制律可表示为

式(20)的积分器容易被一个比例控制器控制，即

式中：ωc为控制器带宽；ntrgt为目标转速．

将式(21)代入式(19)，则控制律为

因而控制整定参数可以概括为：(1)控制器带宽ωc，其可根据目标控制效果进行整定；(2)在进行ESO极点配置时得到的观测器带宽ωo，其值关系到观测器的性能，具体根据被观测对象的响应特性确定，可设定为控制器带宽的倍数关系；(3)通过对象模型得到的控制参数a、b和g．

2.3 模型参数自学习算法

2.3.1 摩擦转矩模型参数自学习算法

为保证摩擦转矩模型的精度，根据式(6)，利用停机过程中转速与摩擦转矩的关系设计针对摩擦转矩参数的自学习算法，如图5所示．

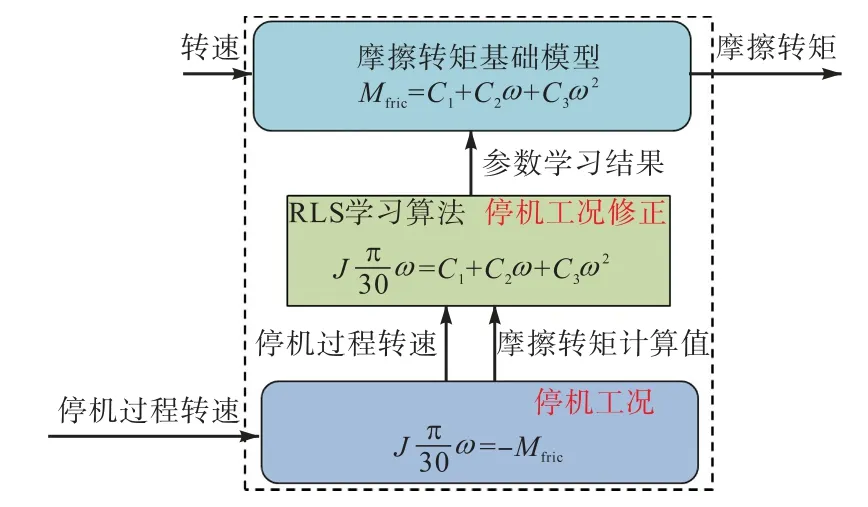
图5 摩擦转矩模型参数自学习算法架构 Fig.5 Self-learning algorithm architecture of friction torque model parameters

摩擦转矩自学习算法的学习过程设定为停机工况，即本次停机过程是修正的本次运行过程结束后，相比于上一次停机过程中摩擦转矩的变化．在实时运行过程中，如果出现运行条件恶化的情况，此时的摩擦转矩模型的偏差则通过笔者提出的转速主动抗扰控制算法的扰动主动观测作用进行补偿．

在断油停机工况，由于自身的摩擦转矩阻力，转速逐渐降低，直至完全停止运转，由式(5)得

系统采样频率为100Hz．转速信号可以直接采集，但是转速的微分信号不方便获取，容易产生噪声，此时，仿真和HIL测试过程中采用差分代替微分的形式，均可以达到设计要求，完成参数的学习过程．对式(23)做离散处理，得

式中：nk为当前采样时刻转速的测量值；nk−1为上一采样时刻转速测量值；Vt为算法调度周期．

式(24)满足：Y(k)=φ(k)⋅θ(k)+w，其中k为当前采样编号，w为噪声干扰．φ(k)和Y(k)为递推最小二乘算法输入，θ(k)为通过递推计算得到的模型参数．

运用带有遗忘因子的递推最小二乘法，在停机工况对式(24)中3个参数进行在线自学习更新．定义

可得摩擦转矩模型参数学习算法为

式中：μ为遗忘因子(0＜μ＜1)；I为单位矩阵．由此可实现对摩擦转矩模型参数的在线更新．

2.3.2 指示热效率自学习算法

为主动适应发动机老化变异造成的发动机热效率下降，设计了针对式(6)中ηin的自学习算法，算法结构如图6所示．

图6 指示热效率自学习算法架构 Fig.6 Self-learning algorithm architecture of indicating thermal efficiency

因式(6)中Mload未知，为降低估计的难度，选择在负荷不变的工况下对喷油量mf引入正弦干扰信号，同步采集该过程中的转速信号．正弦干扰信号的频率主要受到发动机的动态响应速度和热效率辨识速度的影响，1Hz是在两者之间折中优化值．频率太高，则发动机转速波动太小，热效率辨识不准；若频率太低，则热效率学习过程太慢．利用该动态过程的信息进行ηin>的实时估计．首先，对式(6)做离散化，得

式中：Mfric采用摩擦转矩模型计算值，负荷转矩采用RESO的负荷观测值．

式(27)满足Y(k)=ϕ(k)⋅θ(k)+w，k为当前采样编号，定义

根据式(26)递推最小二乘方法，即可递推计算得 到热效率的学习值．

3 算法验证

3.1 主动抗扰控制算法HIL测试验证

3.1.1 硬件在环仿真平台

笔者以台架试验平台为原型，构建HIL测试平台，主要包括发动机实时运行模拟设备、算法实时运行系统和上位机环境3部分．发动机实时运行模拟由dSPACE系统实现，系统搭载的DS1006实时处理器用于实时运行动力系统模型．算法实时运行系统是基于搭载了Infineon多核微控制器的域控制器，算法烧录后实现在嵌入式环境的实时运行．上位机环境包括UDE上位机和ControlDesk上位机，分别实现对域控制器参数和dSPACE运行环境参数的标定和监控．

3.1.2 负荷突增、突减测试

将2.2和2.3节的控制算法生成C代码并下载于DCU中，与dSPACE硬件平台耦合，开展硬件在环仿真测试，包括负荷突变和负荷随机变化测试场景．图7为突变大负荷加载曲线．在负荷变化工况下，对比采用遗传算法进行参数整定后的PID算法[19]和笔者提出的主动抗扰控制算法的转速，如图8所示．

图7 突变大负荷转矩加载曲线 Fig.7 Abrupt change of large load torque loading curve

图8 负荷加载过程转速控制效果验证 Fig.8 Verification of speed control effect during loading

可知，PID算法中转速的抗扰能力相对较差，在第一次负荷加载过程，转速下降幅度为70r/min，2.1s转速恢复为1500r/min稳定转速．主动抗扰控制算法中，转速大幅减小，降至28r/min，改善60%．转速 恢复时间约为1.6s，缩短23.8%．在负荷突减过程，主动抗扰控制算法中，转速上升38r/min，比PID算法改善52.5%．转速恢复时间为1.8s，缩短38.0%．

分析采用降阶ESO的主动抗扰控制算法在转速控制效果上提升的原因发现，降阶ESO有较好的负荷转矩观测速度和准确性，图9为负荷转矩观测值与实际负荷转矩的对比．可知，在负荷转矩突变过程中，降阶ESO能在2～3个调度周期(0.02～0.03s)快速、高效地观测出真实的负荷转矩，从而提高主动抗扰控制算法对扰动的在线扰动补偿能力．

图9 负荷转矩观测值与实际值对比 Fig.9 Comparison of estimated load torque and actual value

3.2 模型参数自学习算法HIL验证

3.2.1 摩擦转矩模型参数自学习算法验证

图10、图11为摩擦转矩参数和摩擦转矩在线学习效果．在硬件在环仿真平台上，首先对摩擦转矩模型参数自学习过程进行了验证，由于是为学习在发动机正常工作转速范围内的摩擦转矩模型参数，因而停 机过程从1500r/min开始，至转速降至0r/min．

图10 摩擦转矩模型参数学习过程 Fig.10 Friction torque model parameter learning process

由图10中参数在线学习曲线可以得出，参数m1、m2和m3经过8.4s左右参数收敛到真实值的5%误差带范围内．由图11摩擦转矩模型学习曲线可得，经过4.5s摩擦转矩模型输出值收敛到摩擦转矩真实值的5%误差带内．

图11 停机工况摩擦转矩模型自学习算法验证 Fig.11 Self-learning algorithm verification of friction torque model under stop conditions

3.2.2 指示热效率学习验证

为保证控制精度，在定负荷工况对ηin进行在线学习．此处模拟燃烧过程恶化而导致的ηin下降情况，ηin约为0.31左右．在硬件在环仿真过程中，经过1.1s左右，ηin的学习值趋近于实际值，学习误差在3%以内，ηin学习结果如图12所示．

图12 指示热效率学习过程验证 Fig.12 Verification of indicating thermal efficiency learning process

3.3 自学习算法对转速控制效果的影响验证

为验证自学习算法对转速控制效果的影响，模拟柴油机运行条件发生恶化的运行场景．通过对摩擦转矩模型参数和ηin的在线学习修正，使得控制算法主动适应柴油机运行条件的变化，实现在线优化控制参数，改善转速控制效果．图13对比了柴油机运行条件恶化前、后负荷突增、突减过程模型参数自学习算法对控制效果的优化．

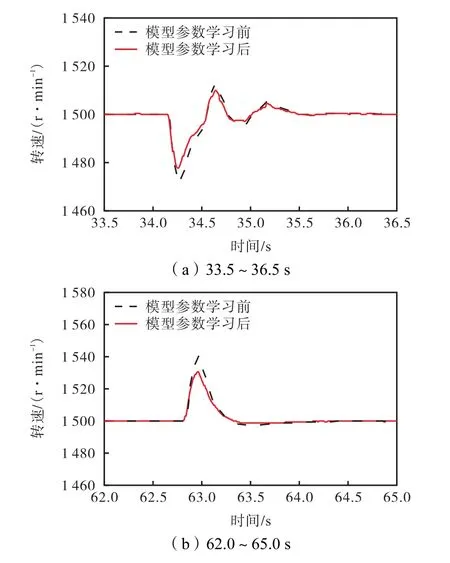
图13 模型参数学习前、后转速控制效果验证 Fig.13 Verification of speed control effect before and after model parameter learning

模型参数学习前、后转速对比表明，通过对摩擦转矩模型参数和ηin的在线学习优化，使得转速波动幅度减小约10r/min，控制效果明显改善，如表4所示．

表4 模型参数学习前、后转速控制效果对比 Tab.4 Comparison of speed control effect before and after model parameter learning

3.4 台架试验测试

数据采集与标定设备采用ETAS ES582汽车标定总线模块．模块通过连接电控单元(ECU)控制器采集运行过程数据，并通过USB接口与计算机连接进行数据标定与分析．所有ES582的测量数据都由INCA(ETAS标定软件)使用ECU信号精确同步．使用测功机模拟用电负荷的变化．按图1中的试验台架结构和数据采集方式进行．试验测试过程主要验证负荷突增及突减过程的转速控制响应，进行了多次负荷突变试验．负荷加载过程转矩如图14所示．

图14 试验过程转矩加载曲线 Fig.14 Torque curve during test

图15为负荷加载台架试验转速控制结果．相比于遗传算法进行参数整定后的PID算法，笔者提出的采用降阶ESO的主动抗扰控制算法的转速控制效果改善明显．

图15 负荷加载台架试验转速控制结果 Fig.15 Rotation speed control results of bench test with sudden load change

在相同的突增负荷工况下，采用降阶ESO的主动抗扰控制算法时转速下降18r/min，1.4s后转速恢复至目标值，达到稳定，而采用遗传算法整定的PID算法转速下降58r/min，在出现约16r/min的超调后恢复至目标值，恢复时间为3.5s．笔者提出的主动抗扰算法在转速的抗干扰能力上比PID算法提升68.9%，恢复时间缩短约60.0%．在突减负荷时，可以控制的能力极限即为停止喷油，发动机根据自身惯性的作用使转速的波动尽可能减小，所以无论是采用遗传算法标定的PID，还是笔者提出的主动抗扰转速控制算法，在突减负荷时都是采用尽快停止喷油的控制法，转速的控制效果也相近，出现约50r/min的转速波动．试验结果见表5．

表5 转速跌落幅值和恢复时间对照 Tab.5 Speed drop amplitude and recovery

图16为PID算法和主动抗扰控制算法喷油量补偿对比．降阶ESO通过增加负荷变化率状态观测并 进一步降低ESO阶次，实现了提升观测精度和观测速度的效果，从而主动抗扰控制算法完成了对需求油量的快速补偿．在负荷突加工况下，降阶主动抗扰控制算法喷油量的补偿速度明显比PID更快，提前约0.16s达到目标喷油量．

图16 75%负荷加载试验结果对比 Fig.16 Comparison of 75% load test results

4 结 论

(1) 通过机理建模和数据驱动建模相结合的方式构建了柴油机曲轴转速动态模型，在此基础上提出降阶主动抗扰控制算法；为提升算法的自适应能力，设计了针对转速动态模型中摩擦转矩模型参数和指示热效率的自学习算法，最终构成了柴油机转速自学习抗扰控制器．

(2) HIL测试表明，通过优化ESO设计方法，增加负荷转矩变化率可观测状态，使得降阶ESO能在2～3个调度周期(0.02s～0.03s)观测出真实的负荷转矩；负荷突变过程观测值也能快速跟随实际负荷转矩值的变化，转速控制效果得到明显提升，转速跌幅大幅减小，降至28r/min，改善60.0%，转速恢复时间约为1.6s，缩短23.8%．

(3) 模型参数自学习算法HIL测试表明，在嵌入式控制器中可以完成在特定场景下的模型参数学习任务；摩擦转矩模型学习可在断油停机过程完成参数的在线学习；在ηin的学习过程中，可以在稳态工况下快速学习得到实际ηin，误差在3%以内；自学习算法开启后转速控制效果提升24.3%．

(4) 采用降阶ESO的主动抗扰控制算法，在负荷突变过程中转速的抗干扰能力得到大幅提升，相比遗传算法整定的PID算法，负荷突增过程，转速下降18r/min，改善68.9%；转速控制响应的恢复时间降至1.4s，缩短约60.0%．