球床式高温堆堆芯气固两相流耦合模拟研究
2022-03-22严安孙喜明董玉杰
严安, 孙喜明, 董玉杰
(清华大学 核能与新能源技术研究院, 北京 100084)
球床式高温气冷堆(high temperature gas-cooled reactor-pebble bed module,HTR-PM)是由清华大学设计,中国华能集团牵头组织在山东荣成石岛湾建设的球床模块式高温气冷堆示范核电站,具备第4代核能系统安全特性的商用核电,2021年12月20日宣布送电成功。示范电站由2个250 MWt的反应堆模块组成,采用球床式堆芯结构,燃料球在重力的驱动作用下缓慢向下移动,实现不停堆换料[1]。稳态运行时,堆芯内不断循环的氦气冷却剂带走燃料球产生的热量,形成复杂的稠密气固两相流系统。
针对HTR-PM球床堆芯的稠密气固两相流系统,研究人员开展了多方面的探索。Zheng等[2]使用安全分析程序THERMIX开展了初步热工分析,随后又使用ATTICA3D和THERMIX对比研究了堆芯的三维热工参数[3],得到了堆芯内压降分布和温度分布等重要结果。Chen等[4]使用THERMIX对HTR-PM稳态平衡堆芯进行了模拟研究,在入口质量流量为100%和90%的保守假设条件下,分析得到堆内最高温度均未超过设计安全限值的结论。彭浩然等[5]使用商用CFD软件ANSYS Fluent及多孔介质模型模拟了HTR-PM球床内的流动与换热现象,验证了多孔介质模型对于高温气冷堆热工分析的适用性。此外,Wu等[6]应用计算流体力学耦合离散单元方法(computational fluid dynamics method and discrete element method,CFD-DEM),结合颗粒辐射模型,在定常物性参数、均匀功率密度下对HTR-10球床堆芯进行了热工模拟,给出了轴向球体表面温度分布。Li等[7]应用CFD-DEM方法,对PBMR球床堆芯进行了多物理场耦合模拟,得到了在氦气流动作用下,球床孔隙率分布的变化,认为冷却剂和球体间的相间相互作用在球床堆芯的热工分析中不可被忽略。在HTR-PM球床堆芯气固两相流系统的热工模拟中,THERMIX是系统分析软件,模拟范围不仅包括球床堆芯,还可以计算堆芯外围的反射层及压力容器等部件,但受限于当时的计算能力,模型较为简化,堆芯使用基于经验公式的二维柱坐标系统进行建模,同时控制方程也较为粗糙。多孔介质方法是在CFD模型基础上,对球床区域进行单独描述,多孔介质区域内采用阻力系数模型和预先设置的孔隙率描述球床对来流流体的影响。CFD-DEM方法则更为精细,由于DEM方法的引入,堆芯球床内球体的运动及每个球体的信息得以解析。特别是随着计算能力的不断发展,目前已逐步具备开展HTR-PM球床堆芯全规模尺度CFD-DEM耦合模拟条件。
本文使用DEM方法,在重力作用下随机堆积生成HTR-PM球床堆芯,对堆积密度分布进行分析;应用CFD-DEM方法,结合经过验证的经验公式及物性参数,对HTR-PM球床堆芯进行建模,并模拟了HTR-PM平衡堆的稳态工况,得出了氦气温度、球体表面温度等重要热工参数的分布,研究CFD-DEM中曳力模型的选取对于计算结果的影响。
1 高温气冷堆数值模型
1.1 堆内热工过程分析与模型框架建立
HTR-PM反应堆模块的一、二回路结构如图1所示,本文选取一回路的球床堆芯作为研究对象。平衡堆芯中共有420 000个直径为6 cm的燃料球,形成了直径为3 m,高11 m的堆芯,250 ℃的氦气冷却剂以96 kg/s的质量流量自堆芯顶部流入,经球床加热后从底部流出。堆芯底部锥角为30°,卸料管直径为0.5 m。
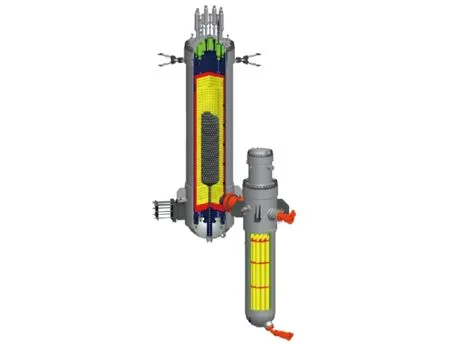
图1 模块式高温气冷堆结构示意Fig.1 Structure schematic diagram of the HTR-PM
在HTR-PM稳态正常运行的工况下,球床中的燃料球处于高温条件,堆芯的传热过程总体可以分为固相发热、气固两相间耦合换热、固相传热和气相导热4个部分。其中,固相燃料球体的发热量主要由热中子通量、235U核子密度和裂变截面决定[8];气固两相间的换热过程中,氦气的强迫对流占据主导作用;固相的传热过程中,主要依靠燃料球体之间的直接接触导热及辐射传热进行热量传递,燃料球-氦气-燃料球的非直接接触导热可以忽略不计;气相间的热量传递依靠流体微团的热力平衡直接计算。
在CFD-DEM方法的框架下[9-10],对球床堆芯内的气固两相分别进行建模,球体的运动由牛顿第二定律决定,球床内空隙处的氦气冷却剂流体由局部平均Navier-Stokes方程描述,并由CFD进行求解。气固两相间的作用力通过对氦气与球体间曳力模型的描述进行建模。堆内热源按功率分布被加载到每个球体上。CFD-DEM耦合的求解逻辑如图2所示:1)进行固相计算,DEM根据现有耦合力、相间热通量和内热源,显式迭代计算至下一个流体时间步,将下一时刻的颗粒位置、速度、温度信息传给CFD;2)CFD隐式求解下一时间步的流场信息,期间由耦合模块对气固两相间的动量以及能量交换进行计算;3)计算更新到下一时间步,CFD将更新的相间作用力和热源通量传给DEM,由DEM进行位置和温度更新,回到步骤1)。

图2 CFD-DEM耦合计算的数值求解逻辑Fig.2 Numerical solution schemes for coupled CFD-DEM computation
1.2 固相控制方程
使用DEM方法对HTR-PM堆芯的固相球床进行建模。在球床的随机堆积和堆内流动过程中,通常考虑球体的平动和转动运动状态,因此,球体i的基本控制方程为:
(1)
(2)

将堆芯内的燃料球简化为等温球体,不考虑内部的温度梯度,建立球体单元i的热平衡方程:
(3)
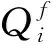
Qij=Hc(Tj-Ti)
(4)
式中:Hc为接触导热系数;Tj为球体单元j的温度。
基于Hertz接触理论,Batchelor等[11]提出了这一系数的近似理论解:
(5)
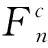
在DEM软件的实现中,使用欧拉格式显式求解式(1)~(3),完成瞬态计算下球体信息的时间迭代更新。
1.3 气相控制方程
在CFD中,气相控制方程主要包括连续性方程、动量方程和能量方程:
(6)
(7)
(8)
式中:ε、ρ、Uf、Tf、p分别为气相的体积分数(孔隙率)、密度、速度、温度、压力;μ为粘性;Fp→f为网格内球体对氦气施加的相间作用力,这里主要考虑曳力,浮力忽略不计;Cp,f为气相比热;Qp为网格内热量源项。
1.4 耦合项的处理及经验关系式
CFD-DEM耦合模拟的关键是对球体-流体的相间作用力和热量交换进行准确建模。相间作用力Fp→f为:
(9)
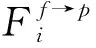
(10)
式中:Ai表示球体沿氦气流向的投影面积;Cd为曳力系数。在本文的研究中,采用Ergun经验公式[12]和KTA阻力公式[2]对曳力系数进行描述。
Ergun经验公式为:
(11)
式中:ΔH为球床区域的高度;dp为球体直径;Us为流体表观速度。Ergun经验公式对应的曳力系数为:
(12)
KTA阻力为:
(13)
(14)
(15)
气固两相间的强迫对流换热采用KTA经验关系式,努谢尔数Nu为:
(16)
式中Pr为普朗特数。
此外,模拟中氦气的物性参数选取,如氦气的密度、比热容、动力粘度和导热系数,均参考德国在KTA 3102.1报告[13]中的安全标准。
1.5 耦合模拟主要参数选取
球床随机堆积模拟中,DEM模型中采用的球床的几何参数和主要物理参数如表1所示。由于球床的堆积结构严重影响稠密气固两相流耦合模拟的孔隙率映射计算,因此杨氏模量E采用9.8×109Pa,为石墨的真实刚度。
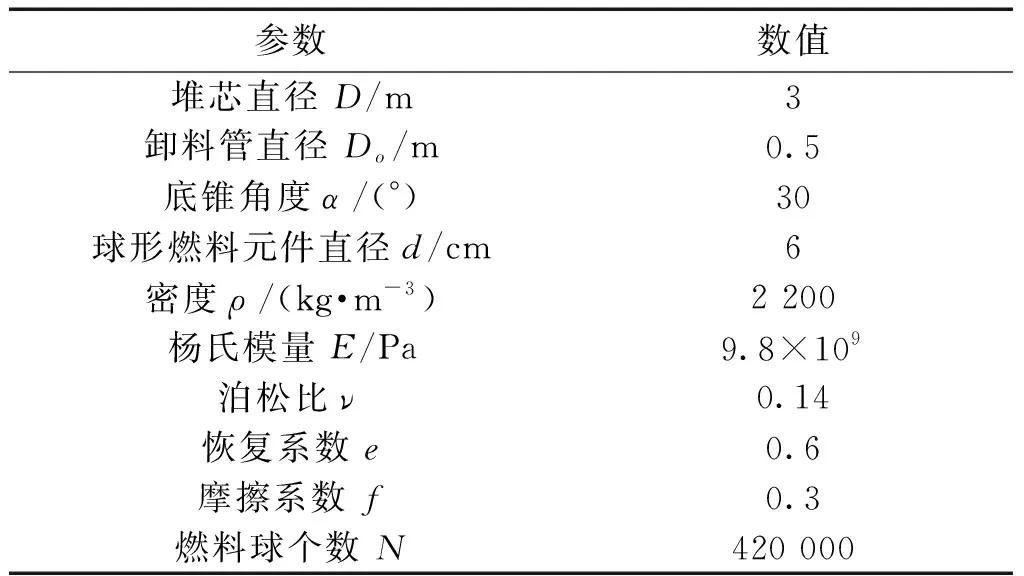
表1 DEM模型主要参数Table 1 Parameters used in DEM simulation
耦合模拟中,CFD-DEM模型所采用的主要参数详见表2。

表2 CFD-DEM模型主要参数Table 2 Parameters used in CFD-DEM simulation
堆芯入口上游边界类型采用速度边界条件,下游边界类型采用压力出口边界,壁面边界类型采用无滑移壁面边界进行模拟。球床堆芯的总功率为250 MW,燃料球的功率密度分布由反应堆物理分析程序VSOP根据HTR-PM平衡堆芯稳态工况的燃料分布情况计算得出,按球体空间坐标经过线性插值处理后,加载在每个球体上,功率密度分布如图3(b)所示。
财政管理人员在管理方面所具备的能力和乡镇财政内部控制在执行方面的效果紧密相关。因此,具有高素质与高技术的财政管理队伍可以保证乡镇财政内部控制的有效实施,并促进内部控制科学性的提升,所以财政管理人员在管理方面的能力就内部控制而言,极其重要。乡镇财政部门在录用工作人员的过程中,需秉承德才兼备以及公平公正的基本原则,采取公开招聘的方式来对人才进行筛选。其次,增强对管理人员的培训与继续教育强度,确保其专业能力可以紧跟时代发展的潮流。重视对相关从业人员的职业道德教育,利用增强奖惩力度的方式来确保内部控制制度的有效实施。
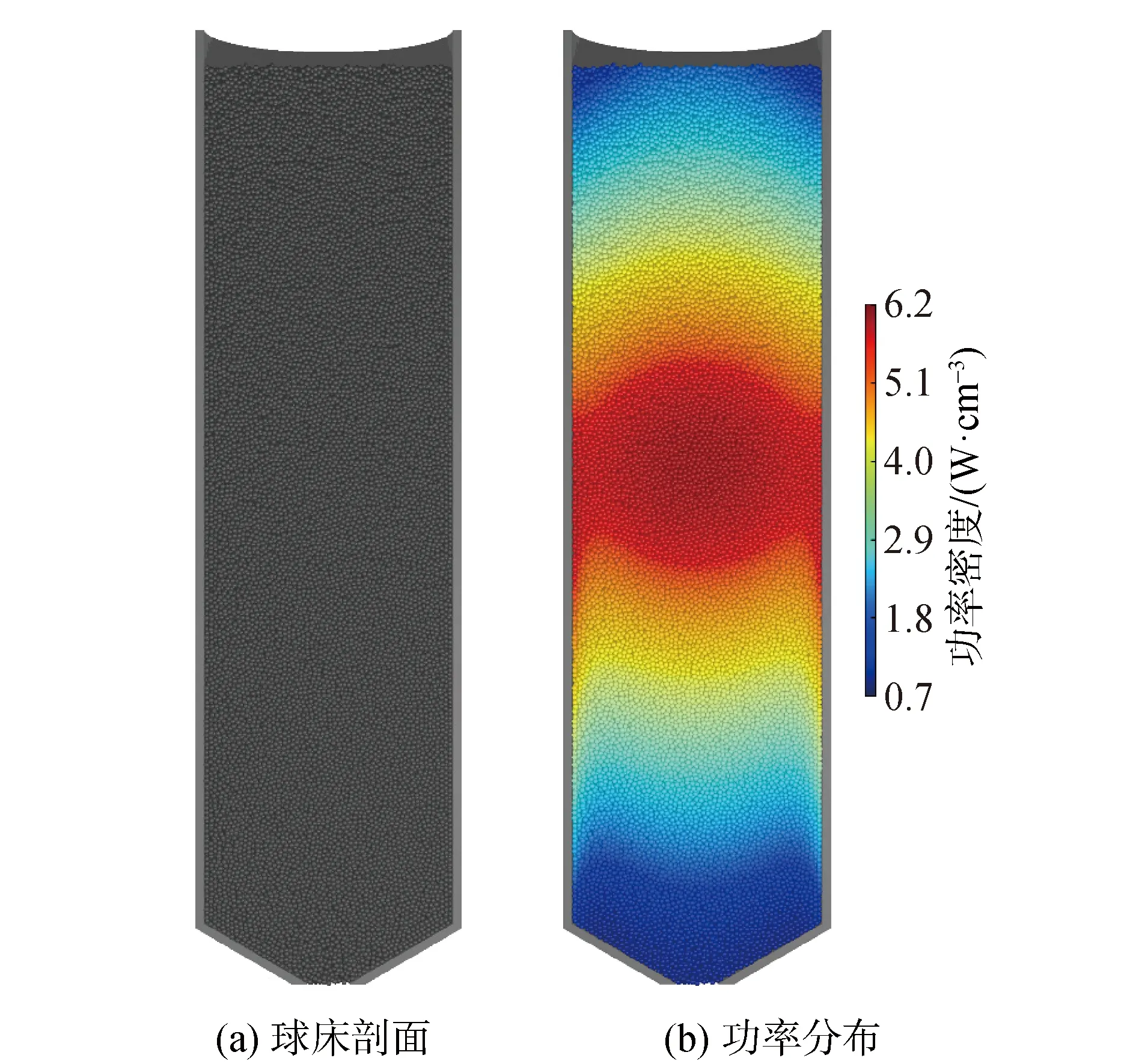
图3 HTR-PM随机堆积球床剖面及功率分布Fig.3 Cross section of initial random packing for pebble-bed core of HTR-PM and its power distribution
2 球床堆积模拟结果与分析
首先使用已建立的DEM模型进行单相计算,获得静态堆积球床供后续CFD-DEM耦合模拟使用。在重力驱动下,球体从堆芯上方空间逐步落入,形成初步随机密实堆积的球床;待420 000个球体完全落入堆内后,对静止球床的准稳态状态继续计算20 s,最终使球床完全静止,壁面对球床的轴向支撑力之和与球床本身总重量的相对误差在10-5以下,可认为球床已经压实,初始堆积完成。对此时的球床堆积结构进行分析,球床堆积结果的剖面图如图3(a)所示。在实际堆芯内部,加球装置位于堆芯中心正上方,随着球体的依次投入形成具有一定堆积角度的斜坡,为方便堆积球床的生成和后续耦合模拟中气固两相交界面的处理,本文将堆顶简化为平面。
采用Du[14]提出的统计方法,对球床的局部堆积密度进行分析,图4所示为球床下半、球床上半及整体的平均径向堆积密度分布。在重力的压实作用下,球床下部的堆积密度比上部更高。堆芯上下2部分与总体平均的分布规律基本一致:靠近壁面的球体在外界几何的约束下排布更加规则,在球体直径d的倍数范围内,堆积密度出现了明显的峰值。距离壁面5d以上的球体约束作用逐渐消失,堆积密度呈现随机小幅波动,不再发生明显的变化。对球床整体进行统计,得到的堆芯平均堆积密度约为61.11%,符合随机最密堆积规律。
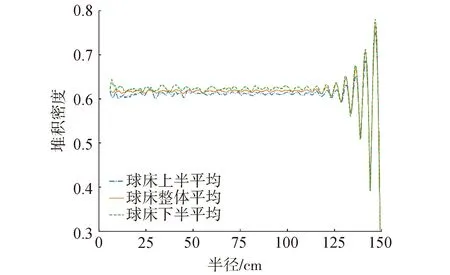
图4 径向球床堆积密度分布Fig.4 Radial packing density profile for packed pebble-bed
轴向的球床堆积密度分布如图5所示,将球床顶部平面记为纵轴的原点。可以看出,轴向堆积密度分布呈现明显的非线性趋势,范围从堆芯顶部的60.0%随着球床高度的增加逐步增大至61.6%。说明随着球床高度的增加,上方球体增多使球床内部压力也随之增加,堆积密度因而增大。1 000 cm处的堆底部,由于接近倒锥区域,堆积密度下降。
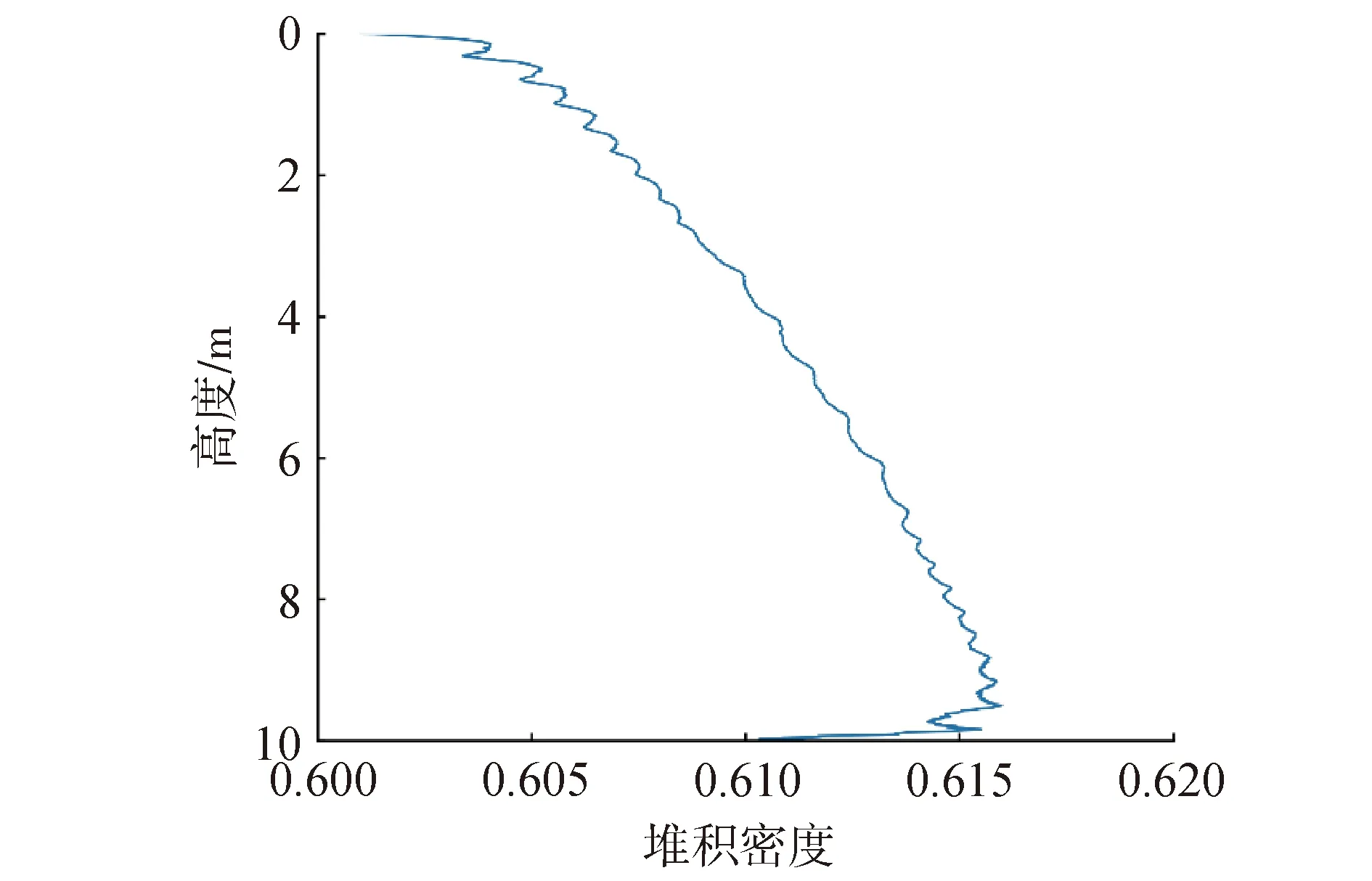
图5 轴向球床堆积密度分布Fig.5 Axial packing density profile for packed pebble-bed
在CFD-DEM瞬态耦合计算中,DEM只负责球体信息的更新和传递,CFD将传入的球体位置坐标映射到控制体背景网格中,气相体积分数即孔隙率ε的计算:
(17)
式中:Vp为单个燃料球的体积;n为落入当前网格内的球体数量;Vcell为网格体积。
图6给出了CFD网格内的径向体积分数分布,可以看出,球体位置信息被正确地处理为两相体积分数参与耦合计算,映射到流体网格后的孔隙率可以一定程度上反映原始球床的堆积密度分布,尤其是在壁面附近可以捕捉到由于球体规则排布导致的孔隙率增大效应。
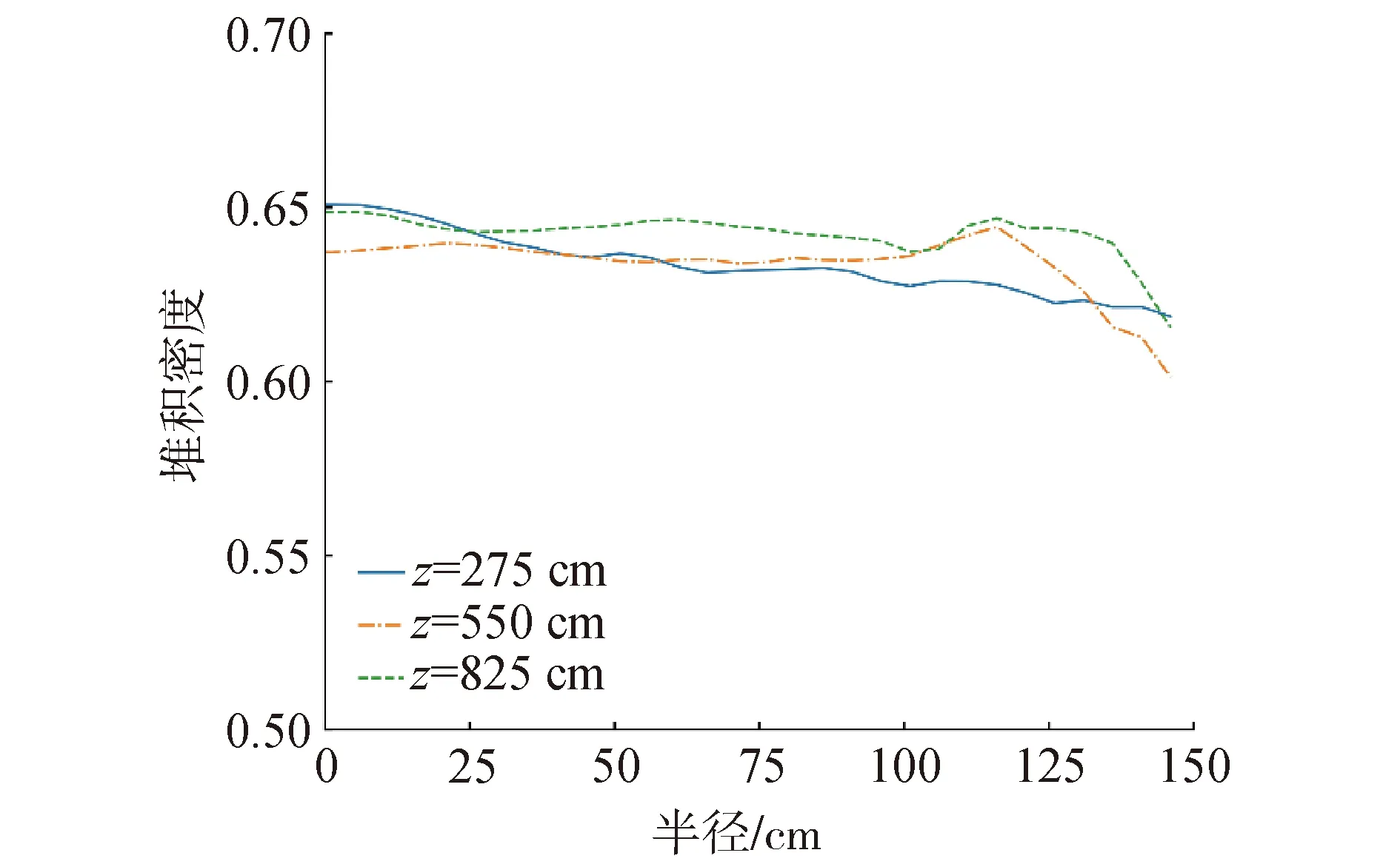
图6 CFD网格内的径向体积分数分布Fig.6 Radial volume fraction profile in CFD cell
3 耦合模拟结果与分析
3.1 堆芯氦气压降
使用KTA压降经验公式和Ergun公式分别完成了HTR-PM平衡堆芯的模拟,图7给出了氦气经过11 m高堆芯的整体压降分布。KTA公式的整体压降在40 kPa左右,Ergun公式计算得到的整体压降在63 kPa左右。Ergun公式所得到的压降结果与Zheng等[2]的模拟结果相当,KTA经验公式偏差较大。使用HTR-PM堆芯内的平均参数,如平均孔隙率ε=0.39、平均氦气温度500 ℃分别代入式 (12)和式 (15)进行分析,得到2种压降模型在耦合模拟中实际提供的曳力系数随雷诺数的变化趋势,如图8所示。可以看出,当Re<103时,KTA压降公式和Ergun公式基本一致;但当Re>103时,Ergun公式得到的曳力系数远大于KTA压降公式;当Re=105时,两者提供的曳力最大相差1.68倍。HTR-PM堆芯氦气流速较高,球床区域的雷诺数在105附近,因此2种模型的计算结果出现了较大偏差。Zheng等[2]模拟中所采用的THERMIX程序和ATTICA3D程序为满足全堆范围的模拟,气相动量方程经过简化,轴向方程中仅包含阻力项、重力项、和压力梯度项。CFD-DEM模型更加精细,由于流体的扩散和对流作用造成的能量损失,计算得到的压降比Zheng等[2]的模拟结果偏低。
3.2 堆芯温度分布
图9和10分别给出了中轴线处堆芯轴向氦气温度分布和燃料球温度分布,可以看出,在球床的内热源作用下,氦气逐渐从堆芯入口处的250 ℃提升至750 ℃,相同位置处的球体表面温度整体比氦气温度高约25 ℃左右。堆芯出口附近的燃料球表面温度没有超过设计限值。图11所示为堆芯入口、堆芯中部的径向温度分布。
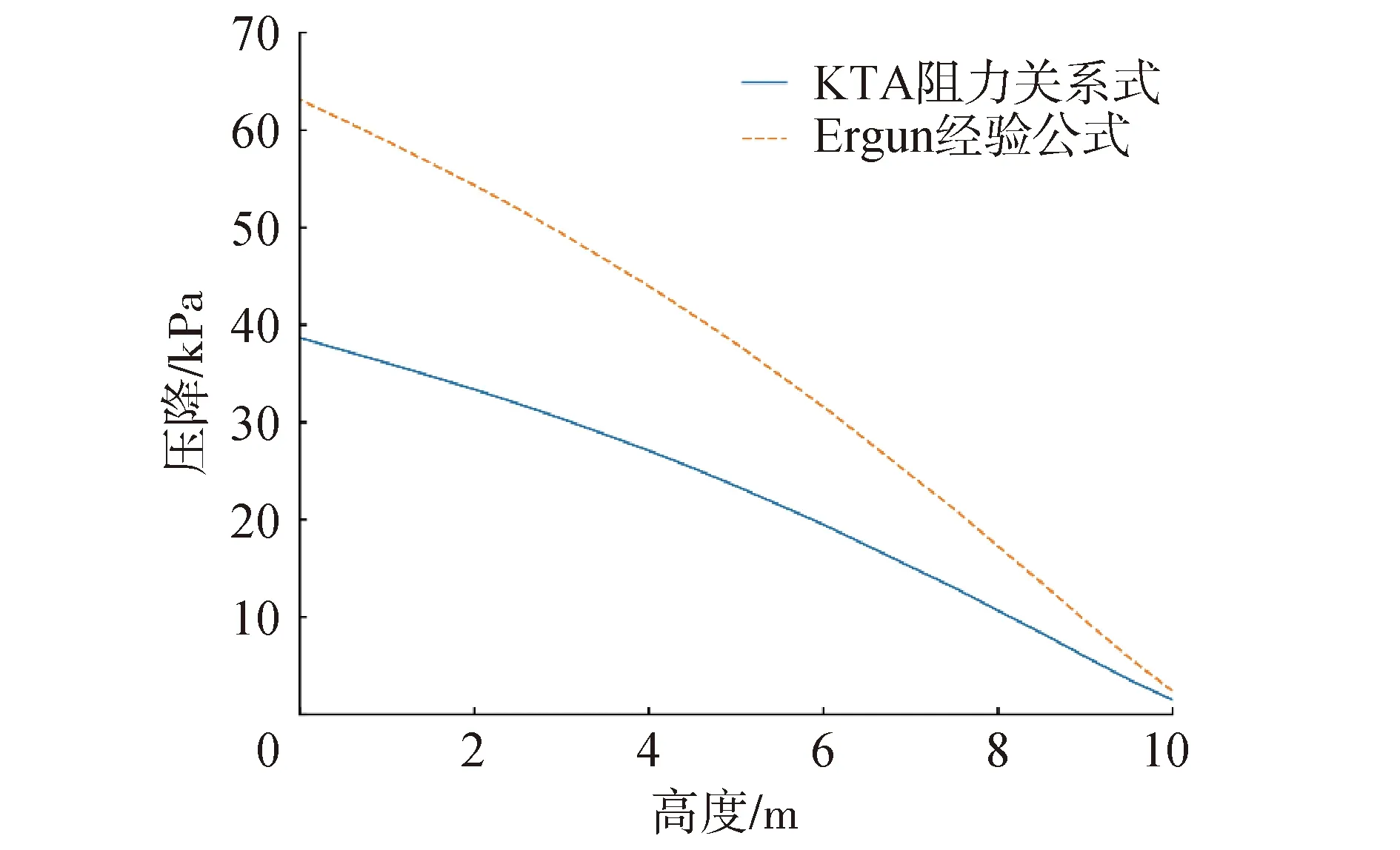
图7 堆芯压降分布Fig.7 Pressure drop profiles in pebble-bed core
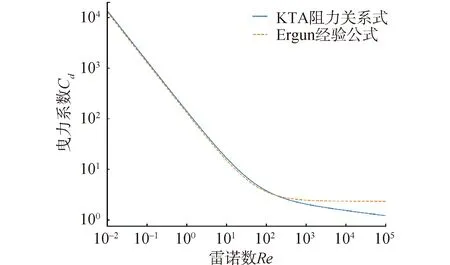
图8 曳力系数随雷诺数的变化Fig.8 Drag coefficient versus Reynolds number

图9 轴向球体表面温度分布Fig.9 Axial surface temperature profiles of pebble
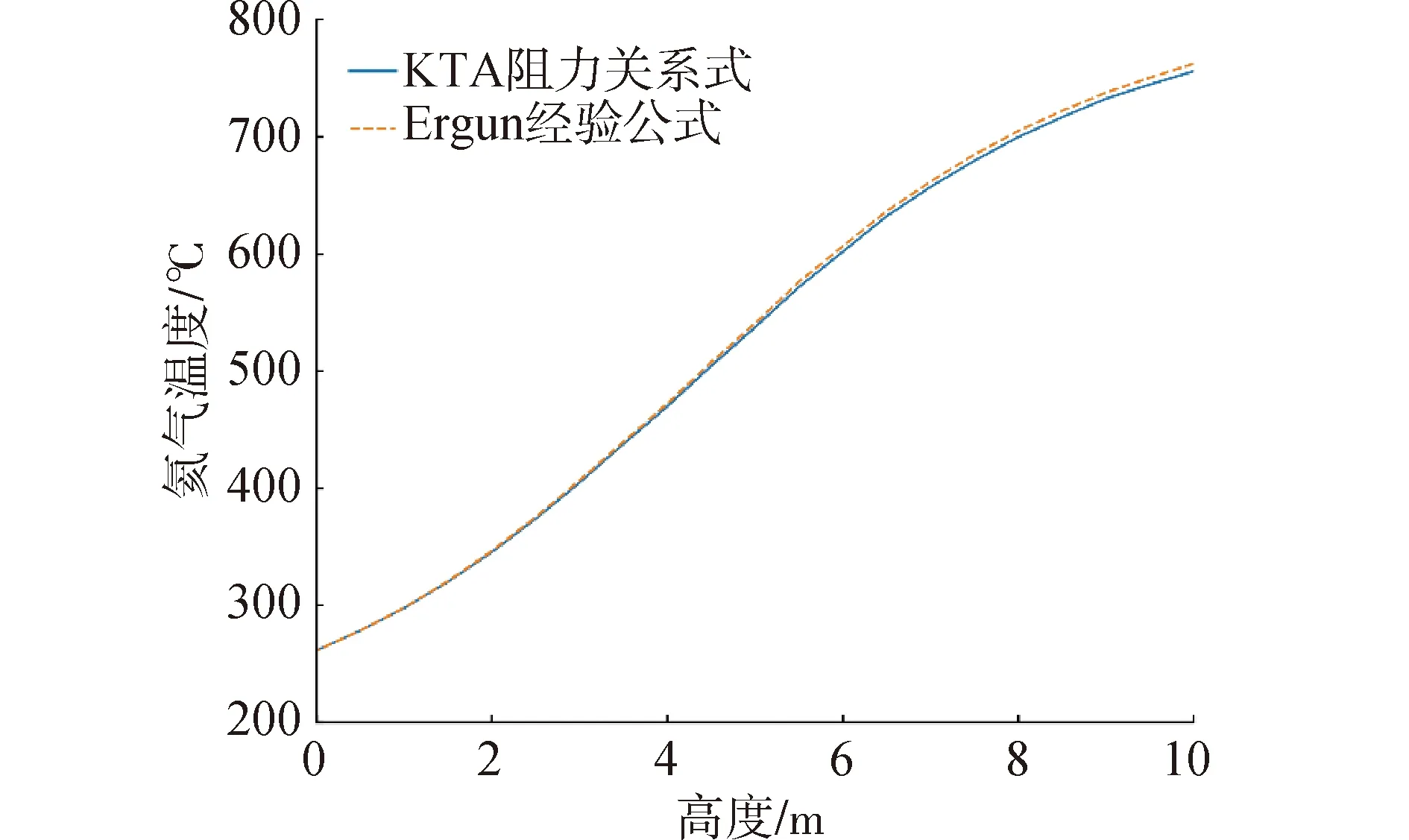
图10 轴向氦气温度分布Fig.10 Axial helium temperature profiles
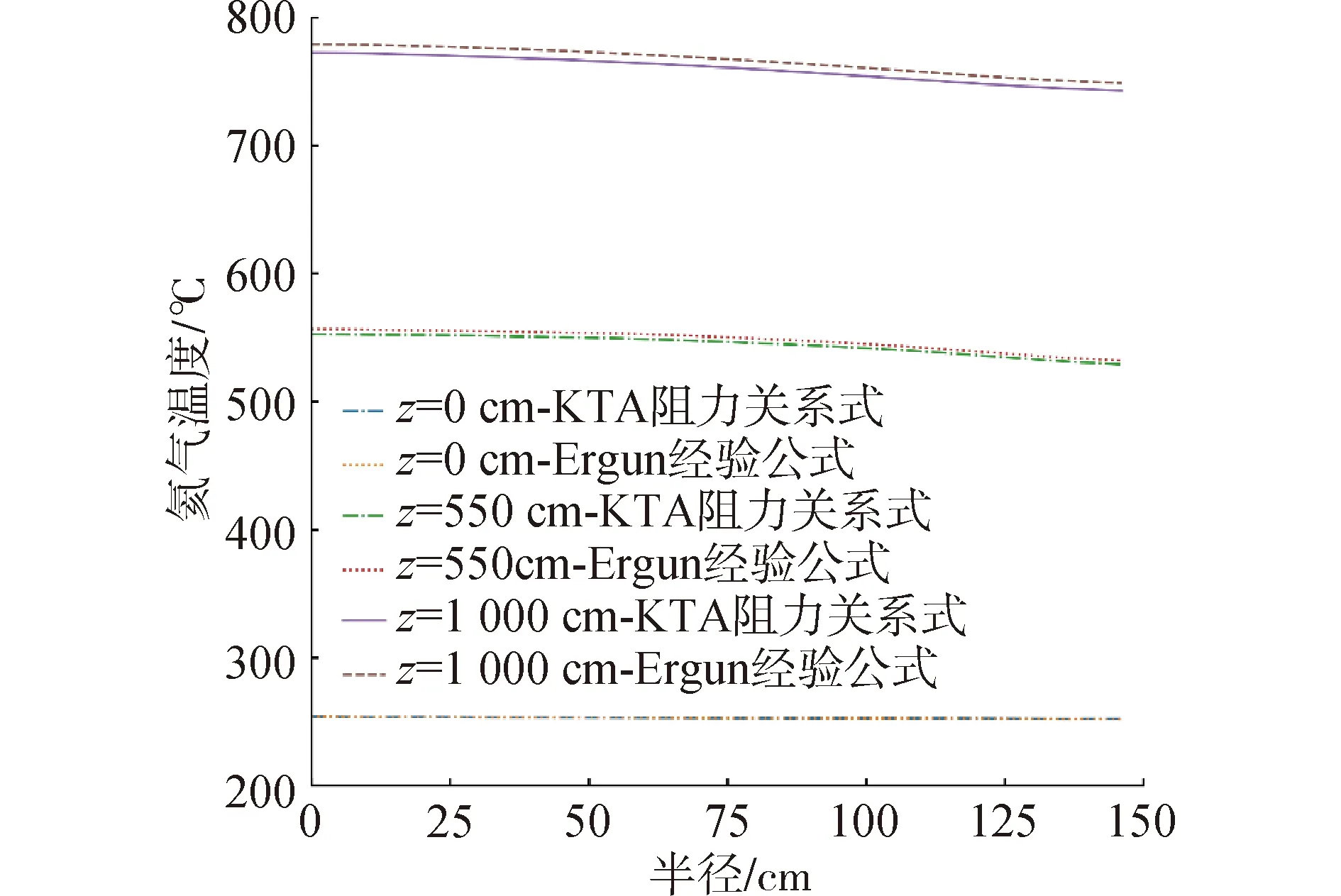
图11 径向氦气温度分布Fig.11 Radial helium temperature profiles
曳力模型的选取对于温度的变化趋势没有明显影响,采用Ergun公式作为曳力模型计算得到的温度整体相对KTA经验关系式略高。这可能是由于曳力模型对压力的影响比较显著,进而影响了当地氦气密度,最终导致温度偏差。
4 结论
1)应用DEM方法,对HTR-PM球床堆芯进行随机重力驱动堆积模拟,生成初始球床,并分析球床堆积密度分布。在重力的压实作用下,球床下部的堆积密度高于上部。
2)对CFD-DEM模拟结果进行分析,得到了氦气温度、球体表面温度等重要热工参数的分布。
3)CFD-DEM中曳力模型的选取对于计算结果的影响较为显著,导致温度偏差。
4)本文可为正在运行的高温气冷堆核电站示范工程HTR-PM的运行与维护提供支持。
后续可进一步针对事故工况开展研究。
