核电厂电动闸阀外漏故障预测方法研究

2022-03-22徐仁义王航彭敏俊刘永阔邓强

哈尔滨工程大学学报 2022年12期

徐仁义，王航，彭敏俊，刘永阔，邓强

(1.哈尔滨工程大学核安全与先进核能技术重点实验室,黑龙江哈尔滨 150001; 2.工业和信息化部核安全与仿真技术重点学科实验室,黑龙江哈尔滨 150001)

电动闸阀是核电厂应用最多且动作频繁的通用设备，其主要用于调节和控制管路中流体介质的流量，由于长时间接触蒸汽、油品和放射性液体等介质，因此随着服役时间的加长不可避免地会出现老化现象。据统计，在核电站中电动闸阀等切断型阀门故障占阀门总故障的1/3左右[1]，因此有必要基于预测性维护理念研究电动闸阀的故障预测技术，计算其剩余使用寿命(remaining useful life，RUL)，从而根据RUL预测结果有针对性地实施维修活动，提高设备的可靠性和运行的经济性。

学者们针对设备的故障预测技术进行了大量研究，在研究方法上可以分为3类[2]，第1类是多元统计分析方法，一般是根据大量运行数据将RUL预测结果以失效概率的形式呈现，但是，这类方法需要假设寿命分布，因此与实际情况有较大差距[3]；第2类为机器学习方法，由于其预测过程具有“黑箱”属性，因此RUL预测结果很难被信服；同时，设备实际运行过程的退化数据获取困难也限制了它的发展；第3类方法则是基于失效机理的物理模型，其通过构建描述设备失效机理的参数化数学模型，结合设备的运行数据或经验知识辨识模型参数, 进而基于运行数据更新机理模型参数实现设备的RUL预测[4]。常用的参数识别主要有粒子滤波[5]、卡尔曼滤波[6]等，而目前，应用最为广泛的机理模型是Paris-Forman模型及其变体形式，徐东等[7]利用改进的Paris模型进行了球轴承的寿命预测。马波等[8]在改进Paris及Forman公式的基础上建立了滚动轴承不同退化阶段的状态空间模型。Chen等[5]将Paris公式融入正则化粒子滤波中，对裂纹进行了疲劳分析。虽然对于一些复杂设备难以解析其故障机理，但是一旦建立物理机理模型，准确度相对较高[9]。

本文以电动闸阀的外漏故障为典型退化模式，分析故障后声发射信号特征参数与故障本身之间的非线性关系，总结形成故障机理模型，构建电动闸阀外漏故障的物理模型，并将其作为粒子滤波(particle filter，PF)的状态空间方程。利用粒子群优化的粒子滤波故障预测模型(particle filter optimized by particle swarm optimization，PSO-PF)实现电动闸阀的RUL预测，通过实验测试证明，所述方法相较于基本粒子滤波模型、长短时记忆网络(long and short term memory network，LSTM)模型具有更高的预测精度。

1 电动闸阀阀体外漏故障机理分析

1.1 电动闸阀裂纹拓展机理模型

由于运行环境的特殊性以及长时间高温高压介质的冲击等原因，阀门有时会产生裂纹甚至破口，而裂纹一旦产生又会由于继续受到冲击而不断延伸扩展，进而影响阀门的密闭性。而在裂纹的拓展过程中，阀门的裂纹稳定扩展阶段是工程实际中考虑最多的阶段，描述此阶段的常用方法有Paris模型、Walker模型以及Forman模型。Paris模型表征整体数据的均值，不考虑应力比的变化。Walker模型考虑了应力比的变化，但相关参数均需要实验数据拟合来获得。Forman模型与Walker模型相似，不同之处在于断裂韧度参数由实验或查手册来获得。为了避免Walker和Forman模型获得材料参数C和m拟合值的困难，且避免实验获得的断裂韧度Kc通常不可靠，本文采取Paris模型研究电动闸阀阀体裂纹扩展过程。在解决实际问题的过程中，Paris公式常常通过差分方程的形式对其进行近似处理：

ak=C(ΔK)mdN+ak-1

(1)

(2)

式中：a为裂纹长度；dN为疲劳载荷间隔；ΔK为应力强度因子幅；下标k表示时间；Δσ为应力范围；C和m为材料参数。

1.2 电动闸阀裂纹拓展的传感感知

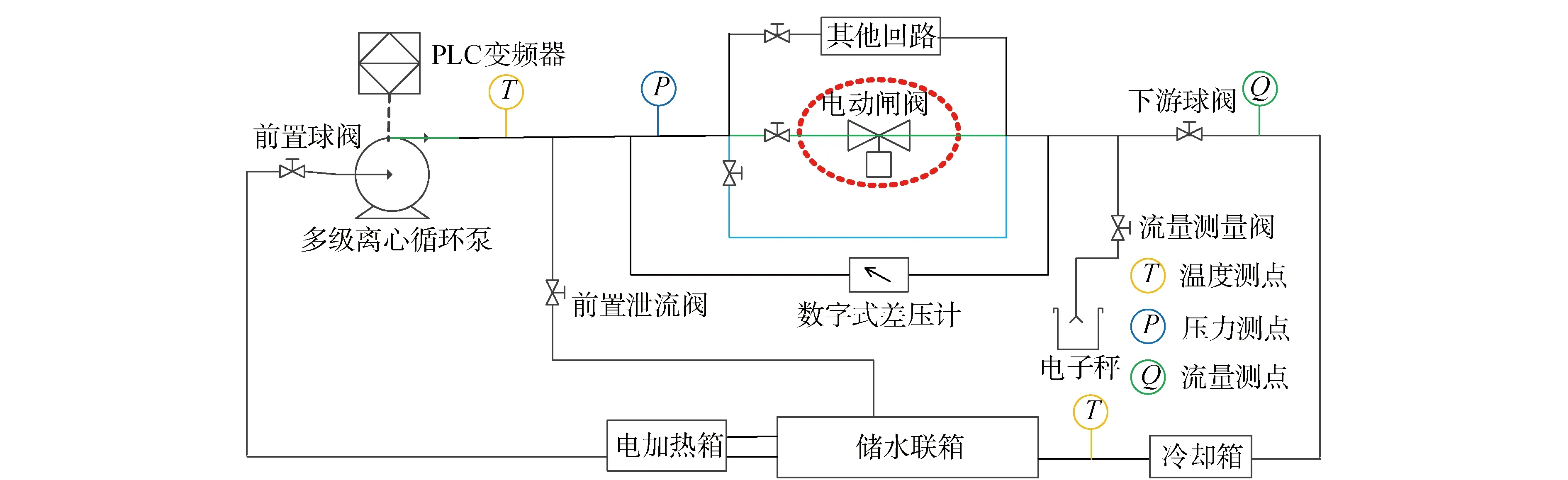
本文通过声发射传感器将难以测量的裂纹长度与实验获得的声发射信号联系起来。由于裂纹拓展造成阀门外漏的模拟是通过在电动闸阀与连接螺丝中间留下缝隙，介质从缝隙漏出来实现的。泄漏量的大小可以通过螺丝松紧程度来调节，当螺丝拧紧时，没有发生泄漏。当螺丝未拧紧时，阀门出现泄漏现象，螺丝越紧，泄漏量越小，反之越大。具体外漏故障件设置与声发射传感器布置如图1所示。

当阀门泄漏发生时，泄漏流体紊流导致产生波动压力场，从而引发声发射信号，信号通过声发射传感器采集完成。因为声发射信号在泄漏孔处的强度最大，且声发射传感器需要安装在较为平整的位置，因此将声发射传感器安装图1所示在电动闸阀阀体底部的平面。

图1 电动闸阀外漏故障设置与传感器布置Fig.1 External leakage fault setting and sensor layout of electric gate valve

在阀门部件表面发生泄漏时，当泄漏孔的压力边界处存在湍流环境时，流体流动的不稳定性导致了流体流动的时间相关性。此时产生的声发射信号为高阶声源释放弹性波。在Lighthill声波方程下湍流产生的声功率为：

Ps=ρv8D2/α5

(3)

式中：v为流体平均湍射流的速度，m/s；α为声音在测试流体中的传播速度，m/s；ρ为阀门泄漏孔处的流体密度，kg/m3；D为阀门的公称直径，m。在实际阀门流体泄漏时，根据流体参数导出声功率：

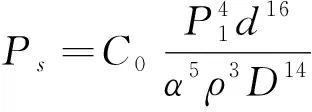
(4)

式中：C0是比例常数；P1为阀门进口压力，Pa；d为阀门泄漏孔等效直径，m。

假设裂纹拓展形状为宽为单位长度l，长为a的长条矩形，则泄漏孔等效直径d为：

(5)

声发射传感器测得的声发射信号均方根值(root mean square，RMS)的平方与阀门泄漏声功率Ps成正比，比例系数设为β，则二者关系为：

(6)

2 粒子群优化粒子滤波的故障预测方法

2.1 基于粒子群优化的粒子滤波方法

粒子滤波算法是一种基于蒙特卡罗方法实现贝叶斯估计的算法，其通过非参数化的蒙特卡罗模拟来实现递推贝叶斯滤波，适用于任何能用状态空间模型描述的非线性系统，因此它为电动闸阀外漏故障预测提供了一种有效的解决方法，粒子滤波的基本理论详见文献[10]。但是基本粒子滤波在滤波估计过程中存在粒子退化问题，即随着粒子迭代次数的增加，大部分粒子的权重会变得很小，只有很少的粒子具有较大的权重。因此为了提高粒子滤波的估计精度，本文利用粒子群算法对重要采样过程进行迭代优化，该优化过程在重要采样过程中引入最新的观测值，并定义适应度函数为：

(7)

式中：Rk为观测值噪声；zNew为最新的观测值；zPred为预测观测值。

粒子群算法通过计算适应度将所有的粒子向最优粒子移动，如果此时粒子均分布在真实状态附近，则每个粒子的适应度均很高，反之每个粒子的个体最优值和粒子群的局部最优值均很低，这说明粒子没有分布在系统真实状态附近。此时，算法通过不断根据最优值并利用粒子速度、位置更新方程实现粒子状态的更新，使粒子不断向真实状态靠近。

(8)

(9)

通过上述移动粒子群向全局最优值靠近，可驱动所有粒子向高似然概率区域运动，当粒子群的最优值符合迭代停止条件时，说明粒子群均已分布在真实状态附近，此时再对粒子集利用最新观测值进行权值更新并归一化处理：

(10)

(11)

式中：N为粒子滤波的粒子数；w为粒子权值。

为解决粒子退化问题，利用重采样算法对权值大的粒子进行复制和选择，实现粒子集合的状态更新。重采样后的粒子状态为：

(12)

式中x为当前时刻的粒子状态。

通过上述的优化过程，使得粒子集在权值更新前更加趋向于高似然区域，从而改善了粒子退化问题，提高粒子滤波的估计精度。

2.2 电动闸阀外漏故障预测流程

基于粒子滤波进行电动闸阀外漏故障的预测时，需要构建用于递推的状态空间模型，本文基于电动闸阀阀体外漏故障的机理分析，利用式(1)和式(6)构建出状态空间模型：

(13)

(14)

式中：uk和vk分别为状态噪声和观测噪声；A为系数。

在状态空间模型的基础上，基于粒子群优化粒子滤波的电动闸阀外漏故障预测流程如下图2所示，其基本流程为：

1)粒子群和粒子滤波算法的参数初始化，设置粒子群算法和粒子滤波算法的粒子数均为100；

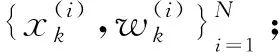
3)粒子重采样：进行粒子有效粒子数的计算并将其与所设阈值Nth进行比较，从而判断粒子退化情况来决定是否采取重采样算法。粒子有效值Neff为：

(15)

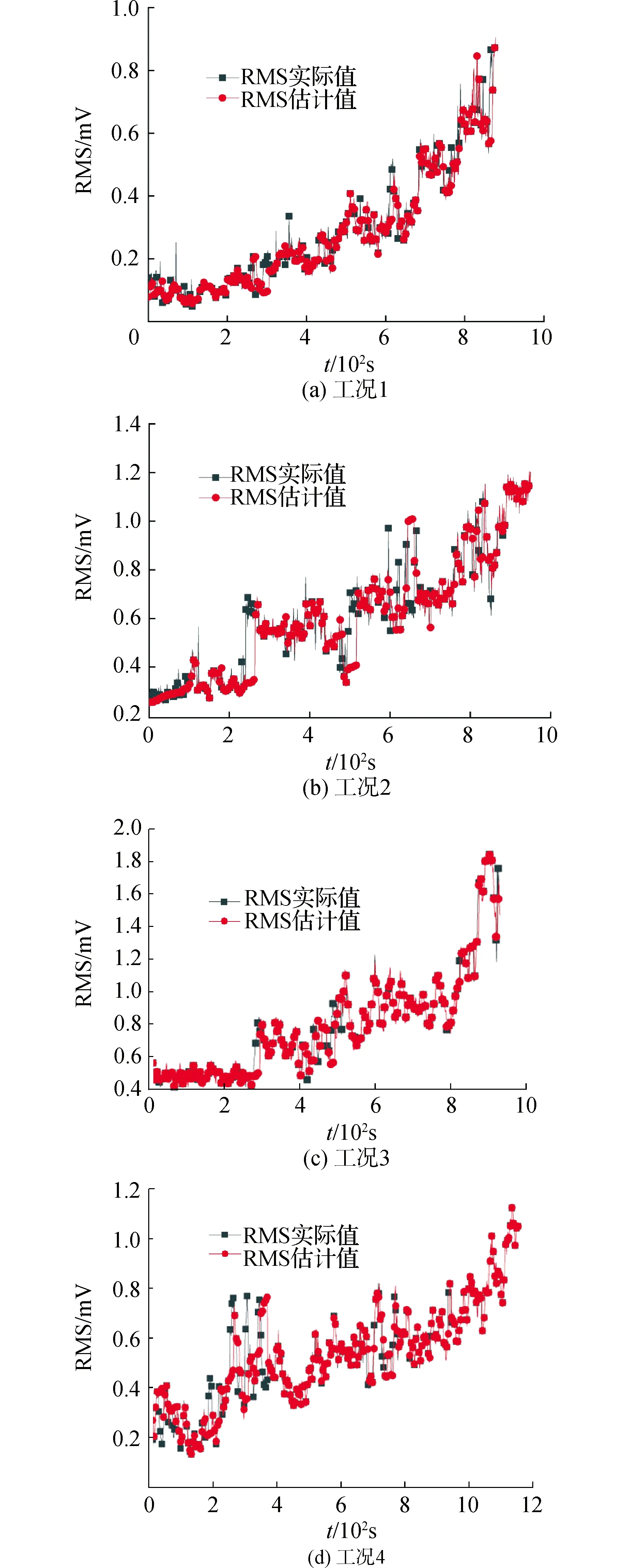
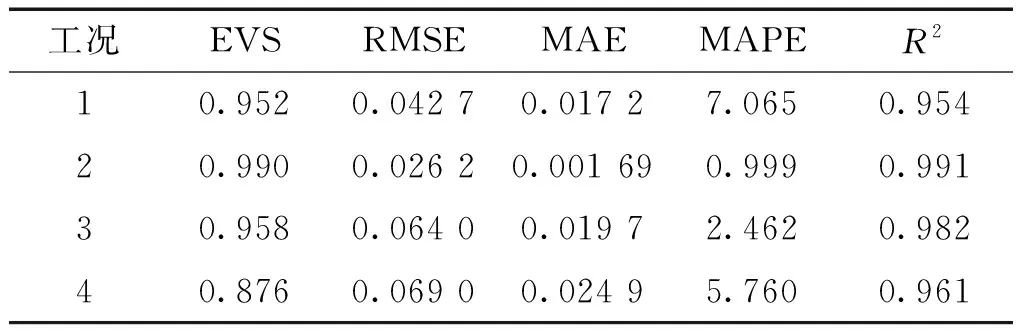
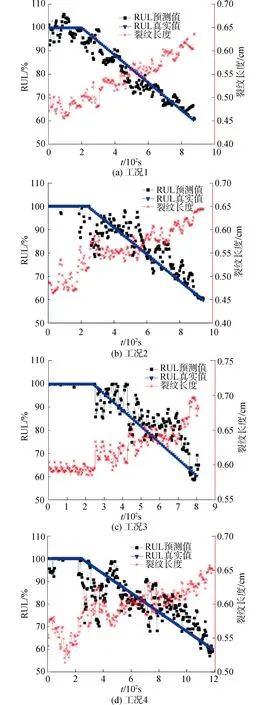
当Neff

4)对每个粒子的状态值依权重值进行加权平均计算，估计kp时刻下的裂纹长度。而后将此时的粒子集合全部代入系统状态空间模型中进行故障预测；当达到故障阈值时，选取所有粒子预测轨迹的中位数为当前时刻阀门的剩余使用寿命，即故障预测结果。下一时刻重复步骤2)、3)、4)，获得完整的裂纹长度变化情况以及电动闸阀的故障预测结果。

图2 基于粒子滤波的电动闸阀外漏故障预测流程Fig.2 Fault prediction flow chart of electric gate valve based on particle filter

3 电动闸阀外漏故障预测分析

3.1 电动闸阀外漏故障试验

本研究搭建了电动闸阀外漏故障模拟的试验台架，用于研究的电动闸阀型号为Z941H-25P直螺杆型闸阀，闸阀采用法兰与装置连接，管道直径为50 mm，同时为防止主管道全部截断时导致泵损坏的情况，在泵出口附近安装了前置泄流阀，可将工质直接引回储水箱，储水箱为敞口容器，最大蓄水量约3 m3。

图3 电动闸阀外漏故障试验台结构Fig.3 Structure diagram of electric gate valve fault simulation test bench

在数据采集过程中，通过声发射传感器获取阀门正常运行状态与阀体外漏状态下的信息。声发射采集卡的采样率为5 000 kHz，实验过程中可以控制的变量为回路的泵频率和阀门开度，泵频率通过控制台经变频器进行调节，阀门开度则可直接通过控制台进行调节。实验共设计5种泵频率和8种阀门开度，共计40个阀门运行工况。实验记录的声发射数据包括振铃计数、声发射信号能量、均方根值以及幅度等。图4所示为泵频率35 Hz、阀门开度30%工况下的RMS数据变化趋势：在一定的泵频率和阀门开度下，随着泄漏量的增加，RMS值的变化总体呈现出单调递增的特性，在泄漏量小于一定值时，RMS值的变化并不明显，而当泄漏量超过这个值时，RMS值的变化会呈现出明显的上升趋势，因此可以得出，通过RMS指标来间接反映电动闸阀外漏故障的退化过程是可行的[11]。

图4 典型工况下电动闸阀状态跟踪结果Fig.4 State tracking results of electric gate valve under typical condition

3.2 电动闸阀状态跟踪结果分析

图5所示为不同工况下基于粒子滤波的RMS跟踪变化趋势，本文选取了4个典型工况，将实验数据RMS值进行提取并作为观测值代入粒子滤波算法，进而基于粒子滤波状态空间模型获得RMS的滤波值。每个运行工况的实验条件如表1所示。

表1 电动闸阀典型工况的运行条件

从各个工况下的RMS跟踪变化趋势可以看出，基于粒子滤波的电动闸阀外漏故障预测模型具有很好的跟踪趋势，能够很好地跟踪电动闸阀的整个退化过程。除此之外，为了定量分析不同工况下粒子滤波跟踪效果的好坏，本项目选用解释方差分EVS、均方根误差RMSE、平均绝对误差MAE、平均绝对百分比误差MAPE以及拟合优度R2等误差指标来分析粒子滤波预测模型的状态跟踪精度，计算结果如表2所示。

图5 不同工况下下电动闸阀状态跟踪结果Fig.5 State tracking results of the electric gate valve under different working conditions

综合上述评价结果可以看出：不同工况下的EVS和R2均处于较高水平，说明模型对于实际退化过程的拟合程度相对较好，同时模型对数据集波动的解释程度较好。虽然个别工况下的MAPE值相对较大，但从RMSE和MAE指标上看，不同工况下的均方根误差和平均绝对误差均处于较小水平，则可说明模型的跟踪误差相对较小，模型具有很好的滤波跟踪特性。

表2 电动闸阀不同工况下RMS跟踪结果误差比较

3.3 电动闸阀故障预测结果分析

电动闸阀的故障预测即是计算设备从当前状态到达故障阈值时的时间，即设备当前时刻的剩余使用寿命(remaining useful life，RUL)。图6为不同工况下电动闸阀剩余使用寿命预测及裂纹拓展的变化趋势图，其中不同工况下电动闸阀外漏故障下的实际退化曲线根据电动闸阀外漏故障模拟试验的实验时间进行线性反演得到。基于粒子滤波的电动闸阀剩余使用寿命预测结果表示裂纹尺寸随时间的拓展趋势。由于裂纹在早期阶段保持稳定，此时退化程度不会明显降低，因此该阶段的裂纹值是恒定的，同时，剩余使用寿命的预测值与实际结果基本一致。而在电动闸阀退化过程中，由于测量不确定度的存在，剩余使用寿命预测值与真实值可能存在误差，这就解释了趋势曲线中存在的较小不匹配。然而，预测值与真实值的退化曲线始终保持一致。各工况反映了裂纹长度与电动闸阀剩余使用寿命之间的变化关系，二者之间的反向变化关系表示当裂纹长度不断增加，电动闸阀的剩余时间逐渐缩短。

为了定量验证模型在不同运行工况下的预测精度，并分析本研究所提方法的有效性，对比分析了所提故障预测方法与基本粒子滤波模型、长短时记忆网络模型故障预测方法的预测效果，基于均方根误差和拟合优度的指标评价结果如表3所示。

表3 不同预测模型下的电动闸阀RUL预测误差比较

从表3的结果误差可以看出，对于不同的运行工况，所提PSO-PF方法的预测误差较小，预测精度也明显大于其他2种方法，模型对数据集的解释程度更好。综合来看，在不同工况下，通过PSO-PF方法得出的寿命预测模型能够较为准确地对电动闸阀外漏故障下的剩余使用寿命进行预测，因此认为本研究所述方法具有较好的实用性和可行性。