混合神经网络的包壳峰值温度预测研究
2022-03-22孙大彬李磊田兆斐王贺
孙大彬, 李磊, 田兆斐, 王贺
(哈尔滨工程大学 核安全与仿真技术重点学科实验室,黑龙江 哈尔滨 150001)
科学认知导致核事故发生的因素,并采取设计、运行与管理措施保护工作人员、公众与环境免受不恰当的辐射危害,是核能可持续发展的重大科学技术问题之一[1]。为了在保证安全性能的同时提高核电厂经济效益,需要对核电厂延寿、老化和核电厂运行变化导致的安全裕度变化开展深入研究。然而传统的确定论安全分析方法(deterministic safety analysis, DSA)和概率论安全分析方法(probabilistic safety assessment, PSA)在核电厂安全裕度分析上都有明显的局限性[2]。为了更加准确的分析核电厂安全裕度,基于风险指引的安全裕度分析方法(risk-informed safety margin characterization, RISMC)成为了研究的重点[3]。该方法采用最佳估算加不确定性分析(best estimate plus uncertainty analysis, BEPU)与先进的概率安全分析方法进行耦合,弥补了DSA和PSA在安全裕度分析中固有的缺陷性,使得准确的评估核电厂安全裕度成为了可能[4]。
虽然RISMC方法已经能够实现安全裕度的准确分析,但是现有的方法在计算效率上面临着巨大的挑战。以RELAP5程序为例,单次事故分析软件程序计算的时间从几分钟到几小时不等,当计算数量激增时,计算量是不能接受的。因此,为了提高RISMC的分析效率,需要采用基于数据驱动的降阶方法提高分析效率[5]。
由于核电厂是一个复杂的、非线性和高度动态的系统,因此许多传统的降阶方法不再适用。而神经网络方法由于其对非线性复杂问题的良好拟合能力,采用训练完备的神经网络模型能够准确、高效的进行计算。文献[6-8]将神经网络方法应用到核电厂复杂系统事故识别及故障诊断领域的分类问题中,取得了很好的效果。文献[9-11]利用神经网络实现核电厂多参数快速建模及优化。Khalil[12]、Kun Mo[13]和Jae-min Yang[14]等已经在核电厂关键参数的短时序预测取得了一定的效果,因此神经网络具备在RISMC分析中应用的潜质。
本文开展了基于神经网络方法的学习模型替代热工水力分析软件计算的研究,通过多方法、多样本对比、超参数优化,实现对核电厂燃料包壳峰值温度(peak cladding temperature, PCT)的准确、快速预测。在对传统的BP神经网络(back propagation neural networks, BPNN)和卷积神经网络(convolutional neural networks, CNN)研究的基础上,提出了一种CNN和长短期记忆法(long short-term memory, LSTM)相结合的混合神经网络(CNN-LSTM)。该混合神经网络利用CNN从历史数据中提取的特征信息结合LSTM方法对时间序列进行预测。
1 混合神经网络建模
BPNN是一种经典、应用广泛的神经网络[15-16]。BPNN主要由学习过程中的信号通过正向的传播与误差的反向传播2个过程组成。本文用到的神经网络也采用这种信息传播方式。CNN[17]相较于传统的神经网络,因其网络结构特殊,能够有效缓解特征提取过程中权重参数数据量过多问题,提高模型预测的准确性,降低模型参数的复杂度,减少模型过拟合现象[18]。PCT预测是典型的回归问题,并且根据事故进程可能是长时间序列的回归问题,因此需要神经网络更好的处理时间序列数据。相较于传统的神经网络,LSTM关注的是序列数据中按照序列顺序的前后依赖关系,在时序数据处理上具备明显优势[19-20]。
本文在保证峰值预测准确的情况下还需要对PCT各时刻的变化趋势信息进行精准预测,以保证尽量全面的捕捉核电厂安全信息。CNN由于其权值共享和局部连接的特性,能够保证在降低网络复杂性的同时,对数据的局部特征和历史序列潜在信息进行捕捉和挖掘。LSTM对时间序列的预测具备良好的精度和鲁棒性,可以反馈长时间序列的影响。因此,本文提出了一种CNN-LSTM的混合神经网络方法,旨在利用各个网络自身的优势,构建高精度、高效率、强鲁棒性的包壳峰值温度长时间序列预测模型。
CNN-LSTM混合神经网络如图1所示。该模型主要包含输入层、CNN层、LSTM层、全连接层和输出层。数据进入输入层完成初始化预处理,满足计算要求后进入CNN层。在CNN层中完成数据特征提取并进行网络稀疏化处理,保证计算精度的同时降低计算成本。构建单层的LSTM结构,对前序特征参数进行学习并寻找数据内部规律。在此之后进入全连接层处理,并在全连接层间增加Dropout函数(Dropout rate=0.5),避免网络过拟合。最终经过多个网络处理输出包壳峰值温度随时间变化的序列。
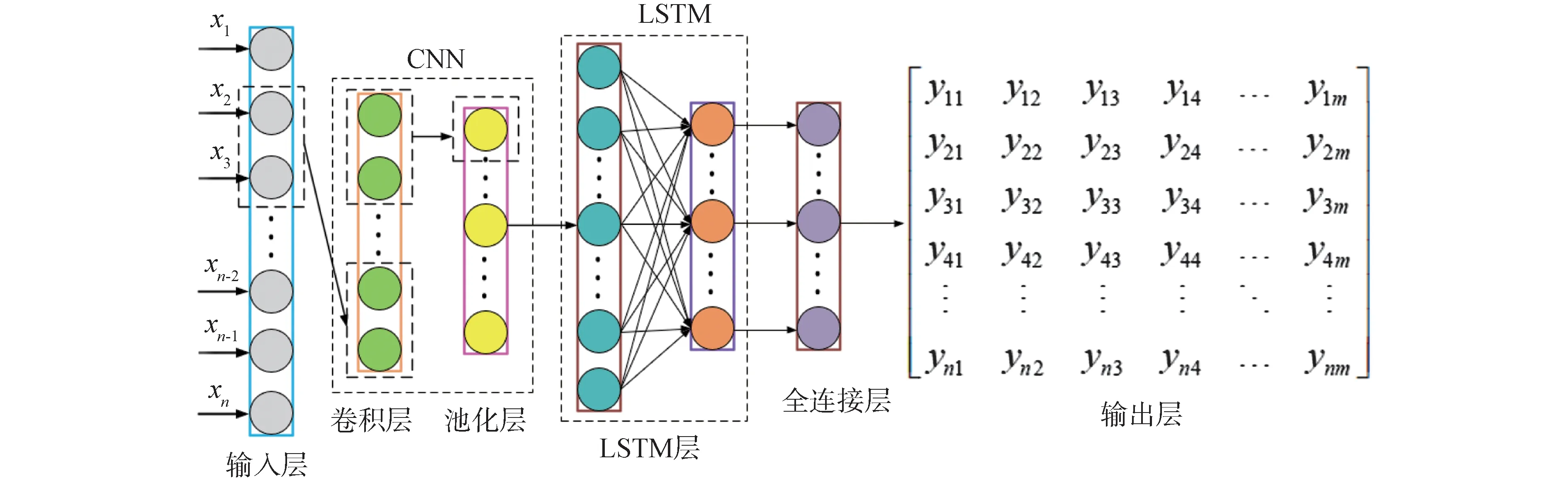
图1 CNN-LSTM结构Fig.1 Structure diagram of CNN-LSTM
2 包壳峰值温度预测验证与分析
2.1 数据选择与预处理
为了更好的说明本文提出的预测模型在核电厂安全裕度分析中的实际工程应用效果,本文选择了秦山核电厂小破口失水事故进行分析。由于事故进程中存在多个分支,对所有分支进行建模需要大量的计算时间和资源,本文选择单列中压安注系统和双列低压安注投入的分支作为算例进行分析。小破口失水事故是设计基准事故,因此可以用作参考的实验数据非常有限,本文采用最佳估算程序RELAP5结果创建事故工况下PCT随时间的变化趋势数据集[21]。该数据集中每个数据采集间隔为1 s,全事故序列长度为3 500 s。该数据集的输入不确定性参数为17个,高维数据包含大量关于观测参数的冗余信息。为了去除数据中的噪声和减少算法的计算时间,需要对数据进行降维。此外,降维有助于泛化能力。降维的目的是寻找一种能有效描述高维数据特征的低维表示,以避免维数过多问题。数据降维方法可分为特征选择和特征提取两种。本文选择Spearman相关性系数算法进行数据特征选择[22]。Spearman相关性系数为:
(1)
式中:di表示第i个数据对的位次值之差;n表示总的样本个数。通过Spearman相关性系数筛选得到的不确定性输入参数数据如表1所示,其中所有不确定性参数符合均匀分布。

表1 不确定性参数表Table 1 Parameters for uncertainty analysis
根据表1数据可知,不同参数数据之间存在明显的量级差别,该现象会导致很大的奇异值,严重影响预测模型的收敛速度和数据结果可靠性,因此需要进行数据预处理,将数据线性变换到[0,1],计算公式为:
(2)
式中:xmin是最小值;xmax是最大值;x是待处理数据;xs是预处理后的数据。
2.2 模型评价指标
为了评价不同模型的预测能力,需要采用一些评价指标来描述预测精度。本文选择了6个评价指标,分别为均方误差(mean squared error, MSE)、均方根误差(root mean square error, RMSE)、平均绝对百分比误差%(mean absolute percentage error, MAPE)、峰值温度绝对精度% (peaking temperature accuracy, PTA)、概率预测精度% (probability prediction accuracy, PPA)、过拟合度(degree of excessive fitting, DEF)分别为:
(3)
(4)
(5)
(6)
(7)
(8)
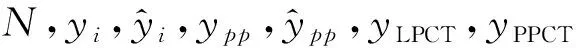
2.3 模型超参数优化及样本数量分析
神经网络模型中的超参数深刻影响着预测模型性能,因此需要对预测模型进行超参数优化,本文对CNN-LSTM混合神经网络的模型超参数优化过程进行详细的介绍。常用的超参数优化方法主要有:人工经验判断、网格搜索法、高斯过程法、人工神经网络稳健分析法[23]。其中人工经验判断偶然性较大,高斯过程法需要充分的先验知识,人工神经网络稳健分析法实现过程相对复杂,因此本文采用应用广泛的网格搜索法进行超参数优化。本文涉及的优化超参数为迭代次数(epochs)、批处理大小(batch_size)、激活函数(activation function)、优化函数(optimization function)、学习率(learn rate)和网络节点数(nodes)。所有超参数进行统一网格搜索计算量过大,因此采用两两超参数组合进行优化、分析。神经网络的超参数优化旨在找到相对较好的超参数组合而非全局最优组合,因此该测试方法具备可行性。
2.3.1 迭代次数和批处理
迭代次数是指向前和向后传播中所有批次的单次训练迭代。原则上迭代次数越大,预测模型收敛性能越好。然而在实际测试中,迭代次数在达到一定次数后模型就比较稳定,因此为了在保证精度的同时尽量提高分析效率,需要确定合适的迭代次数数量。批处理大小是指一次训练所抓取的数据样本数量,批处理大小会影响训练速度和模型优化效果。5个不同批处理大小的迭代结果如图2所示。数据结果表明,当迭代次数次数达到800时,各预测模型均已收敛,因此模型迭代次数设置为800。
不同batch_size的各评价参数对比结果如图3所示。数据结果表明,batch_size=32的模型的PTA和序列预测精度(sequence accuracy, SA)达到了99.1%和91%,具有很高的预测精度。RMSE和MAPE均是各模型中最小的,具备最好的稳定性和精度。并且其超限概率预测准确率为95.4%,明显高于其他batch_size,说明其对学习样本的峰值分布统计规律也能够进行有效的学习,能够达到安全裕度分析的要求。虽然各组过拟合度结果不尽相同,但均没有明显的过拟合或欠拟合现象。综合各评价参数,选择batch_size=32进行预测模型构建。
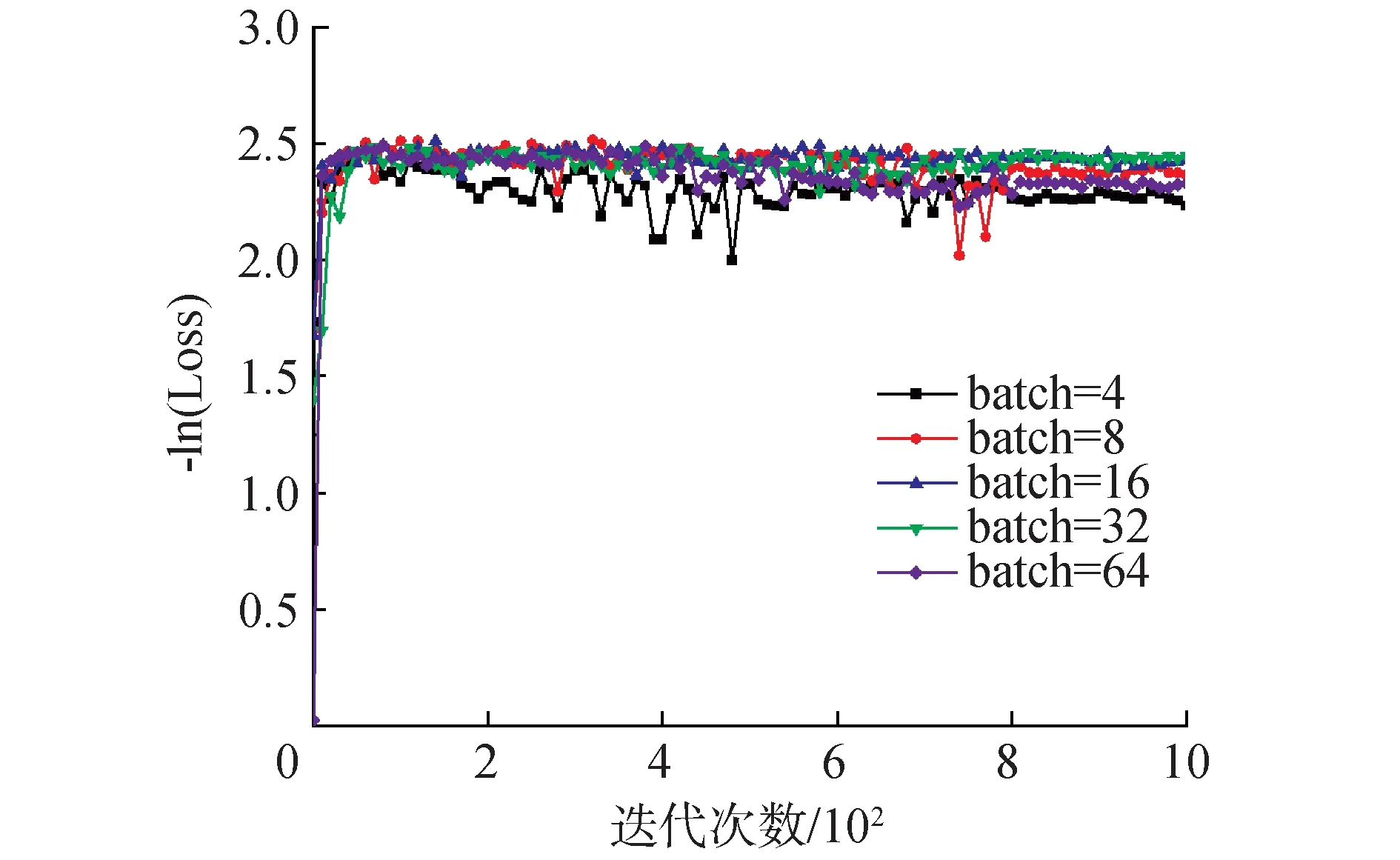
图2 不同模型的误差随迭代次数变化趋势Fig.2 The loss of different models varies with the number of epochs
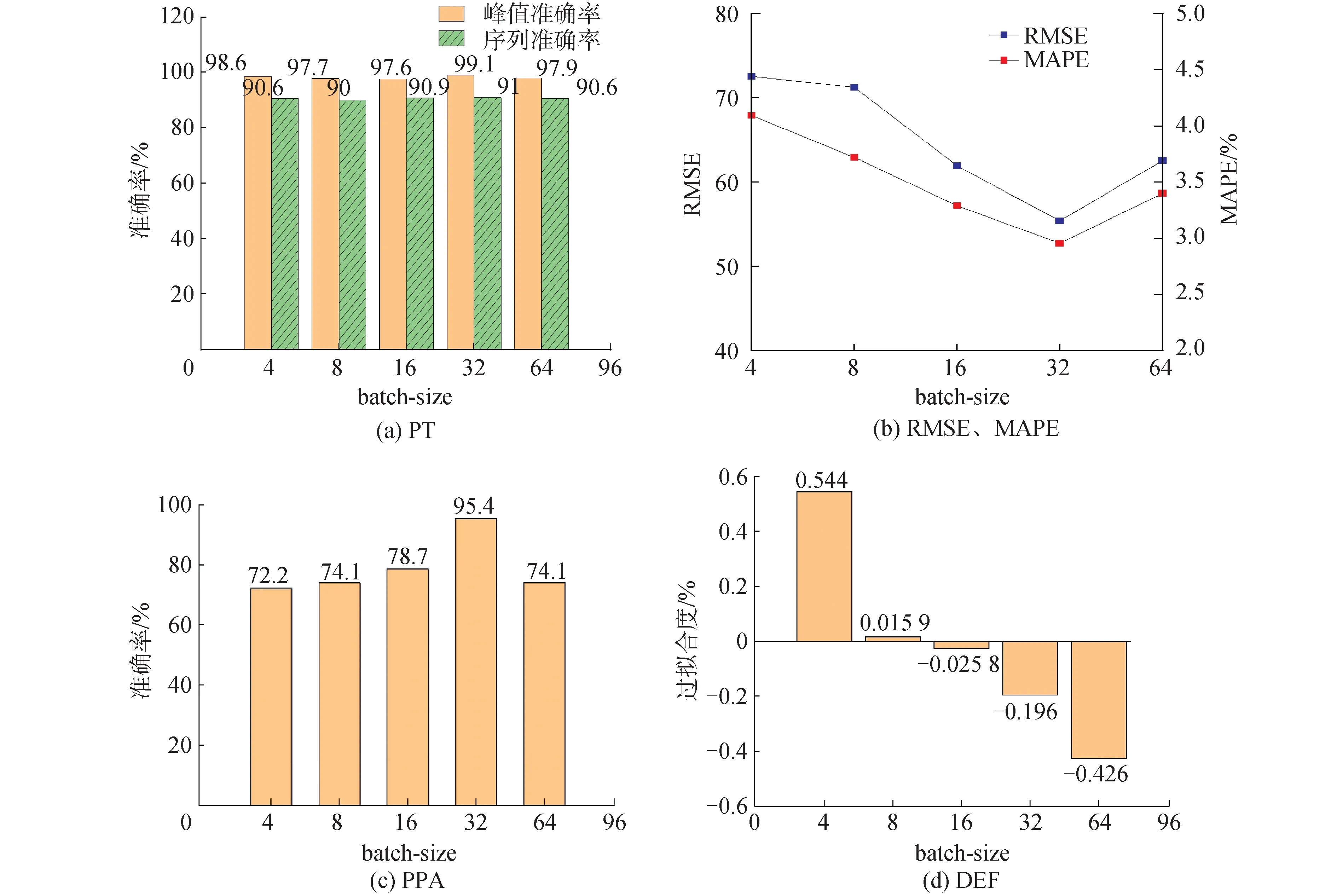
图3 不同batch_size评价参数对比Fig.3 Comparison of different batch_size evaluation parameters
2.3.2 激活函数和优化函数
激活函数就是在神经网络的神经元上运行的函数。激活函数可以是非线性的,这就增加了神经网络模型的非线性因素,为预测非线性问题提供了可能,激活函数的选择非常重要。本文研究中选择了2种饱和激活函数Sigmoid和tanh以及3种非饱和激活函数ReLU、Leaky ReLU和RReLU。优化函数是神经网络中决定权重系数更新效率和精度的关键,本文研究中选择了4种常用的优化函数:随机梯度下降(stochastic gradient descent, SGD)、Adadelta、Rprop、Adam。各组合评价参数结果对比如图4所示。不同数值大小的含义同2.2节所述。
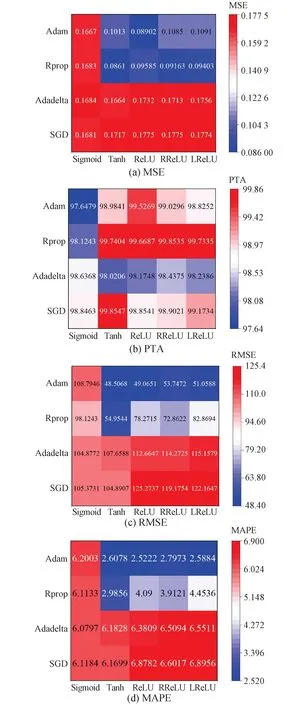
图4 不同组合评价参数对比Fig.4 Comparison of different cases evaluation parameters
数据结果表明,Sigmoid激活函数由于主要应用于分类问题,因此在峰值温度序列预测的各个评价参数中效果最差。Tanh函数作为激活函数在超限概率预测上精度明显劣于ReLU、Leaky ReLU和RReLU。优化函数中,SGD方法由于完全依赖于batch的梯度,容易收敛到局部最优,因此相关预测模型的鲁棒性和精度均较差。Adadelta、Rprop对学习率进行了一定的约束,相对于传统的SGD方法其预测的准确性和鲁棒性均有明显的提升。Adam作为带有动量项的Rprop,它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率,每一次迭代学习率都有个确定范围,使得参数比较平稳。数据结果也表明Adam优化函数在各优化参数中具备准确的预测性能和稳定性。通过综合对比分析,ReLU和Adam的组合性能最佳,因此选择二者作为预测模型的激活函数和优化函数。
2.3.3 学习率和节点数
学习率作为优化算法中的调谐参数,可以确定每次迭代中的步长,使损失函数收敛到最小值,因此对预测模型的收敛性、预测精度等都有重要的影响。学习率设置过小则收敛速度过慢,学习率过大则可能导致无法收敛及精度较差。学习率的选择没有标准的选择规定,因此需要对不同的模型进行测试。本文在经过预测试后选定了6个不同的学习率进行优化测试。神经网络中每个隐藏层的节点个数也对预测模型的效率和精度有重要影响。节点数过少,网络不具备必要的学习能力,节点数过多会导致网络结构复杂,在对硬件提出更高要求的同时降低分析效率。一般情况下,当精度接近时要选择节点数较少的模型[24]。测试案例对应具体数值如表2所示。
各评价参数对比如图5所示。其中颜色越接近红色表明数值越大,越接近蓝色则数值越小。不同数值大小的含义同2.2节所述。数据结果表明,节点数500,学习率5×10-3的组合以及节点数400,学习率5×10-4的组合在各个评价参数上均表现出良好性能。为了提高预测模型的分析效率,选择节点数更少的400,5×10-4组合作为预测模型的节点数与学习率。

表2 测试案例与具体数值对应表Table 2 Test cases correspond to specific values
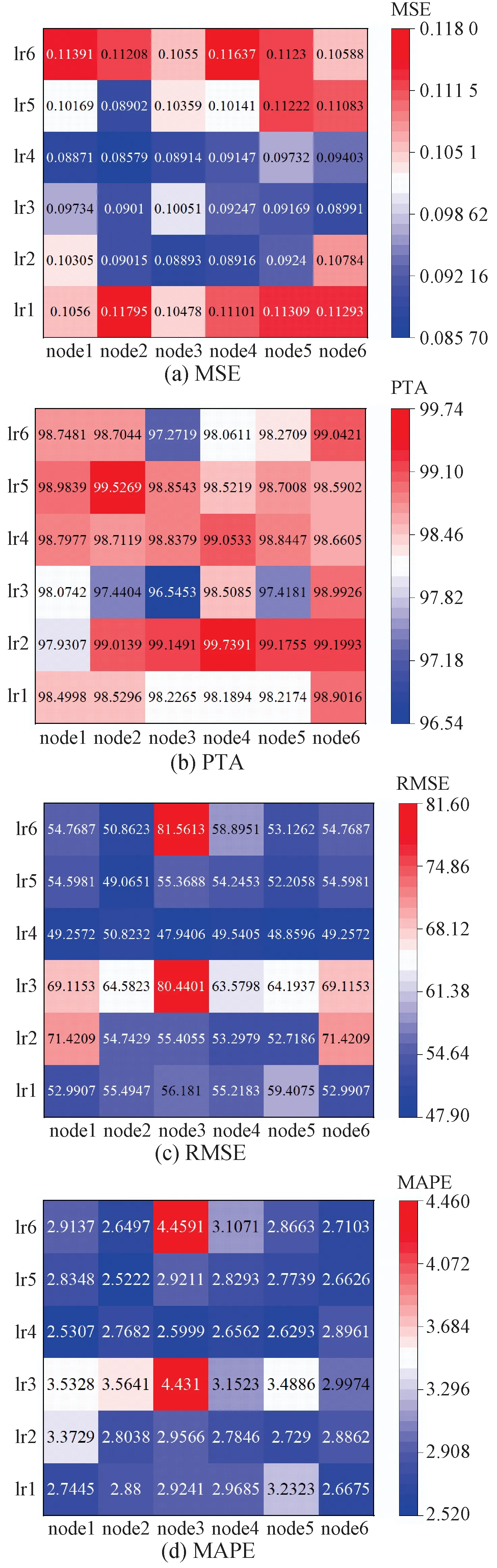
图5 不同组合评价参数对比Fig.5 Comparison of different cases evaluation parameters
2.3.4 样本数量
在神经网络学习中,理想条件下学习样本数量越大模型越容易获得较好的性能,然而在实际应用中受限于实验数据采集、计算机资源以及计算效率需求等多种因素,不可能无限的扩大样本数量。因此需要在保证精度要求的前提下采用尽量少的样本。不同样本下预测模型各性能指标数据如图6所示。当样本数量为500时,预测模型性能较差,难以满足预测需求。当样本量不少与1 000时,预测模型各评价指标均有明显提升且模型性能较好,并且由于数据本身的均衡性,并没有出现评价指标随样本规模增加而集体变好的现象。本文采用Intel(R) Xeon(R) W-2275 CPU 3.30GHz CPU进行RELAP5分析计算构建数据库,单算例一次计算需要411 s。每增加1 000组样本计算时间需要增加约114 h。图7、8展示了不同样本数量下全序列和2 700~3 000 s内的峰值温度预测结果,其中真实值是指RELAP5程序运行结果,其余几组为混合神经网络预测结果。数据结果显示在样本数量不少于1 000时,各预测模型在全序列和峰值出现的关键时间段内均具有很好的预测精度,没有出现明显的精度差异。在平衡了预测模型性能和计算效率后选择1 000组样本进行预测模型建模。
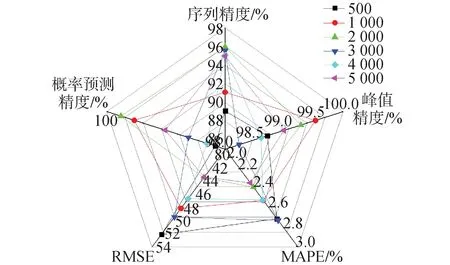
图6 不同样本数量评价参数对比Fig.6 Comparison of evaluation parameters with different number of samples
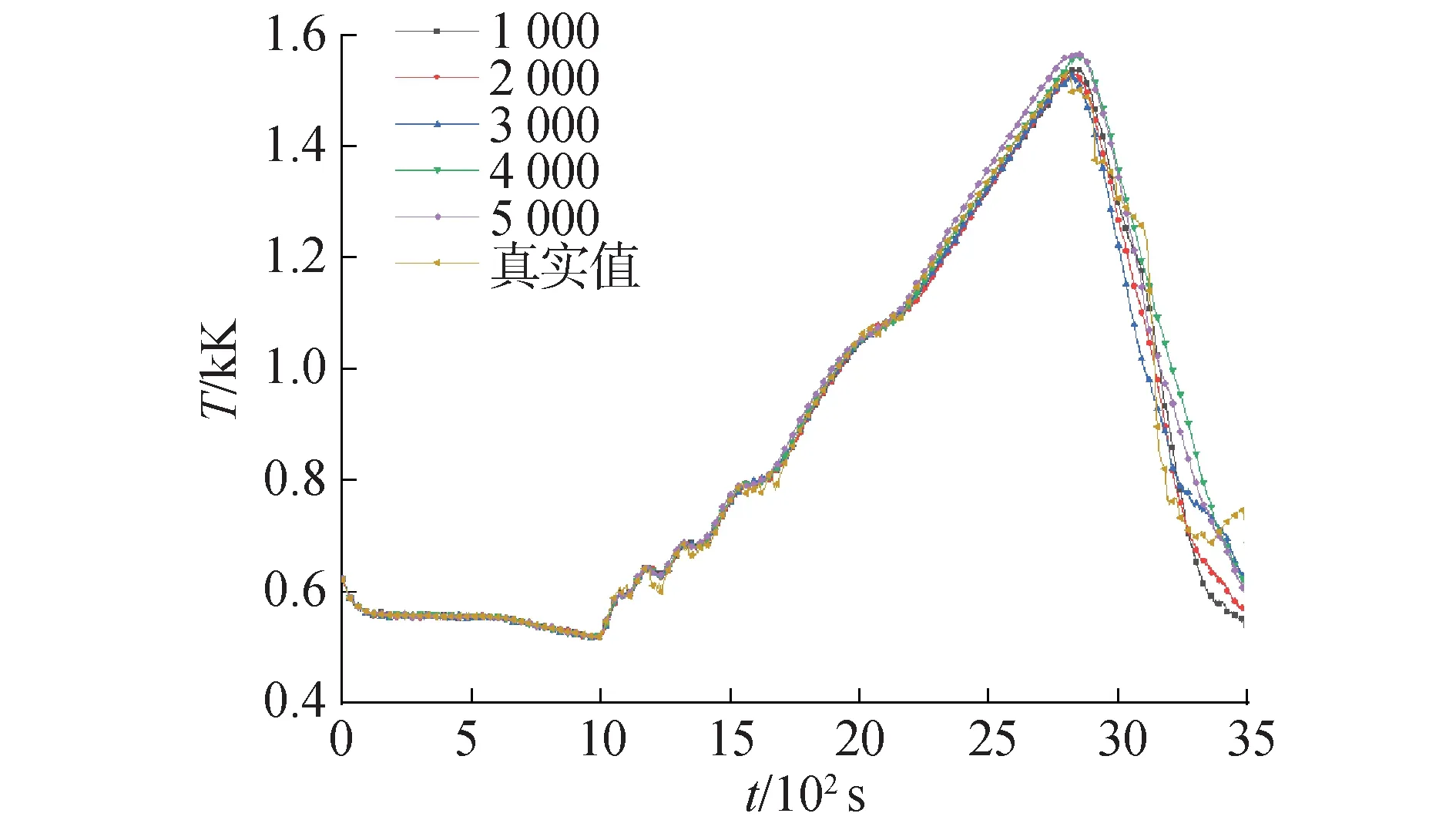
图7 不同样本数量全序列预测PCT对比Fig.7 Comparison of PCT predicted by whole sequence with different number of samples
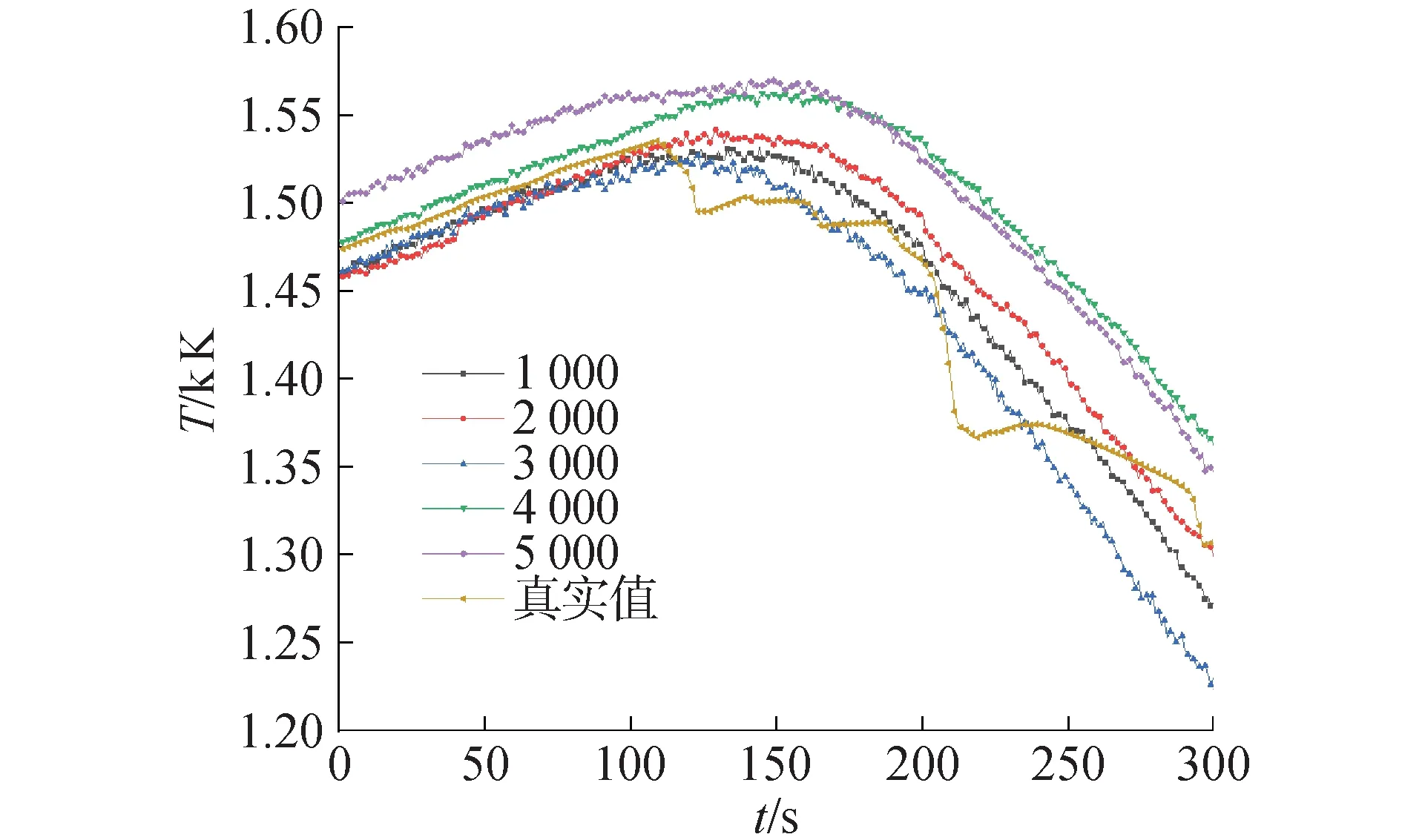
图8 不同样本数量部分序列预测PCT对比Fig.8 PCT comparison of partial sequences predicted by different number of samples
2.4 模型性能比较
为了验证混合模型在预测精度和稳定性上的进步,将其与CNN和BPNN进行对比分析。在使用相同的训练和测试数据集训练所有模型后,预测PCT以进行性能评估。本文涉及的模型均采用Python编写,使用Pytorch深度学习框架。各评价参数数据对比如表3所示。数据结果表明,CNN相较于BPNN在峰值预测和全序列预测精度上有明显进步,体现了CNN对数据局部特征更强的学习效果,然而在模型的稳定性和对统计数据预测上并没有体现出优势,反而数据结果要劣于传统的BPNN。混合神经网络CNN-LSTM充分融合了各个神经网络方法的优势,在各性能指标上均有明显优势。峰值精度提高了0.786%和0.691%,序列精度提高了1.289%和1.173%,RMSE降低了6.886%和22.356%,MAPE降低了5.331%和11.664%,概率预测精度提高了8.423%和14.446%。预测效率上,均采用NVIDIA GeForce RTX 3080 GPU进行预测,预测200组数据所需时间分别为110、111、110 s,单组预测时间为0.55、0.56、0.55 s,没有明显的区别。这充分表明新的方法在保证计算效率的同时,准确提取局部数据特征的情况下,在建立长期依赖关系上体现了优越的性能。3种方法的过拟合度都非常小,因此3个模型均可以应用在PCT预测研究中。
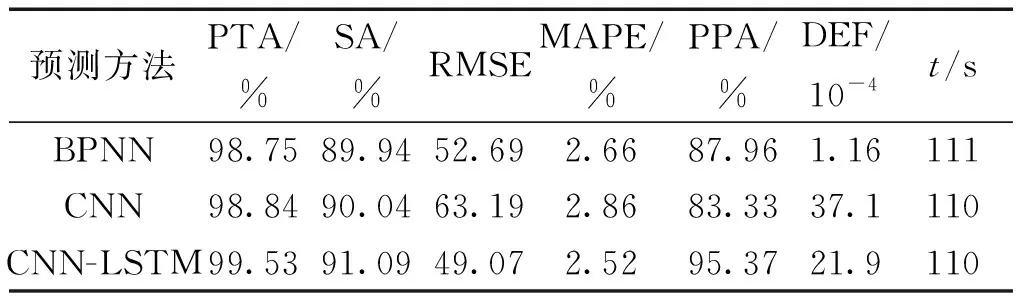
表3 不同模型评价参数对比表
3 结论
1) 当样本数量达到1 000时,经过超参数优化的CNN-LSTM模型的峰值预测精度、序列预测精度、超限概率预测精度、MAPE分别达到了99.527%, 91.098%, 95.371%, 2.522%满足预测精度需求。RMSE为49.065,满足模型稳定性要求。过拟合度为2.191×10-3,不存在过拟合或欠拟合现象。单次事故分析时间从RELAP5系统仿真程序的411 s降低为0.55 s,分析效率提升了747倍。
2) 混合神经网络CNN-LSTM与传统BPNN和CNN相比,对数据局部特征和时间序列信息的学习上有明显提升,在进行长时间序列包壳峰值温度预测时,模型精度和稳定性有明显的提高。
3)本文提出的混合神经网络模型对包壳峰值温度的预测达到了较高的精度的同时,明显提升了包壳峰值温度计算的效率。与现有预测方法相比,对包壳峰值温度的全时间序列信息预测精度更高,可以为核电厂安全裕度分析提供更多、更准确的信息。
后续将针对更多的事故序列进行预测分析,对算法的适用性进行进一步的验证。
