基于注意力机制的CNN-GCN模型及其应用
2022-03-22李继龙霍纬纲
李继龙,霍纬纲+,李 勤
(1.中国民航大学 计算机科学与技术学院,天津 300300; 2.京北方信息技术股份有限公司 IT服务交付中心部北京平台,北京 100032)
0 引 言
多变量时间序列预测在经济学、金融[1]、生物信息学和交通[2,3]等领域有着巨大的应用。多变量时间序列预测方法内在地假定变量之间有相互依赖关系。换句话说,每个变量不仅取决于其历史值,而且还取决于其它变量。然而,现有的方法并没有有效地利用变量之间潜在的相互依赖关系。首先考虑多变量时间序列(multivariate time series,MTS)的统计方法。如自回归(autoregressive,AR)模型和高斯过程(Gaussian process,GP)模型是经常用到的基线方法。二者均假设变量之间存在线性依赖关系。为了建立非线性关系,采用了AR的一些变体,如向量自回归多层感知器(vector autoregressive multi-layer perceptron,VARMLP)模型。最近基于深度学习的MTS预测方法得到了快速发展,依次提出了卷积神经网络(convolutional neural network,CNN)模型[4]、门控循环单元循环神经网络(gated recurrent unit recurrent neural networks,RNN-GRU)模型[5]、长短期时间序列网络(long-and short-term time-series network,LSTNet)模型[6]、双自注意力网络(dual self-attention network,DSANet)模型[7]和用图神经网络进行多变量时间序列预测模型(multivariate time series forecasting with graph neural networks,MTGNN)[8]。
上述方法大多从提取MTS时序特征角度建立了预测模型,DSANet和MTGNN预测模型同时考虑MTS的时间和空间特性,但是DSANet中采用的自注意力机制无法很好表达MTS各变量间的依赖关系,MTGNN采用图卷积网络提取了MTS的变量之间的空间依赖关系,但其捕获时序特征的子模块较复杂。为了实现对多变量时间序列准确和稳健的预测,本文提出了一种融入图卷积网络、注意力机制和卷积神经网络的三通道网络框架模型,实验结果表明了本文中所提出的模型方法有较好的MTS预测效果。
1 背景知识
1.1 GNN和GCN
图神经网络[9](graph neural network,GNN)在处理网络中实体之间的空间依赖关系方面取得了巨大成功。图神经网络假设节点的状态取决于其邻居的状态。为了捕捉这种类型的空间依赖,通过消息传递[10]、信息传播[11]和图卷积[12]开发了各种图神经网络。Marco Gori等发表论文,提出了图神经网络的概念。随后,其在两篇论文中又进一步阐述了图神经网络,并提出了一种监督学习的方法来训练GNN。图卷积网络(graph convolutional network,GCN)是GNN的一种,采用卷积算子进行信息汇聚。卷积神经网络在视觉领域取得令人瞩目的成绩,于是人们开始考虑如何将卷积应用到图神经网络中。Kipf等[12]将频域图卷积的定义进行简化,使得图卷积的操作能够在空域进行,这极大地提升了图卷积模型的计算效率,同时,得益于卷积滤波的高效性,图卷积模型在多种图数据相关的任务上取得了令人瞩目的成绩。近几年,更多的基于空域图卷积的神经网络模型的变体[13,14,10]被开发出来。
1.2 注意力机制
注意力机制[15]就是让神经网络具备有选择的去关注输入中的某一部分的细节信息的能力。注意力机制允许对依赖关系进行建模,而不考虑它们在输入或输出序列中的距离。注意力机制自从被提出以来就受到了人们的关注和追捧。因其良好的性能效果,已成功的在多个领域的多个任务上得到了应用。
自注意力(又称内部注意力),是注意力机制的一种形式,它涉及单个序列的不同位置,用以计算序列的表示。自注意力机制已成功地应用于多种任务,比如阅读理解、文本摘要、文本蕴涵和与任务无关的句子表示学习[16]等。多头注意力就是根据多个查询来计算和选取多个信息的。多头注意力能够很好模拟人类视觉注意力机制的原理过程。在很多任务中的序列建模和构建转导模型时,多头注意力机制成为可供选择的一个很好的组成部分。
2 问题描述
时间序列X(i)=〈x1(i),x2(i),…,xT(i)〉 是一个一维时序测量序列,其中数量XT(i)是在时间戳T的记录。通常,两个连续测量之间的时间间隔是恒定的。多变量时间序列表示为X=〈X(1),X(2),…,X(D)〉, 其中X中的时间序列相互关联,向量XT∈D是在时间戳T的记录。
给定一组多变量时间序列X=〈X(1),X(2),…,X(D)〉, 其中D是单变量时间序列的数目,X(D)∈T,T是输入窗口的长度,本文以滚动预测的方式进行多变量时间序列的预测。也就是说,基于已知的 〈X1,X2,…,XT〉 来预测XT+h,其中h是当前时间戳前面可取的时间间隔范围(Horizon)。同样,基于 〈X1+k,X2+k,…,XT+k〉,k∈+预测未来XT+h+k的值,假设窗口内的信息足以满足预测需求,窗口大小是固定的。因此,设定预测目标XT+h∈D, 在时间戳T的输入矩阵为X=〈X(1),X(2),…,X(D)〉∈D×T。
3 基于注意力机制和图卷积的神经网络模型
3.1 时间序列预测模型的整体架构
基于图卷积网络和注意力机制,构建一种多变量时间序列预测模型简记为DSAGCN(dual self-attention graph convolutional network),本文称之为“基于注意力机制的CNN-GCN”,其整体的框架结构如图1所示。
基于注意力机制的CNN-GCN模型由图学习层模块、图卷积层模块、局部时间卷积模块、全局时间卷积模块、自注意力模块和输出模块6部分构成,详细介绍如下。
图学习层模块自适应地学习图的邻接矩阵,以捕获MTS各序列之间的空间依赖关系。M(本文中M取的是5)个图卷积模块间加入了残差连接跳跃连接,以图的邻接矩阵和MTS数据样本为输入,聚合MTS各序列与其邻接序列的特征。局部卷积模块通过卷积单元、池化单元、自注意力单元和前馈神经网络单元4部分,提取MTS数据样本的局部时态特征。类似地,全局时间卷积模块通过卷积单元、自注意力单元和前馈神经网络单元三部分,提取MTS数据样本的整体时态特征。自注意力模块分别捕获全局时间卷积和局部时间卷积结果的时态空间依赖关系,并将结果同时输入进全连接层。最终将全连接层的输出与图卷积模块的输出相加得到整个模型方法的预测值。
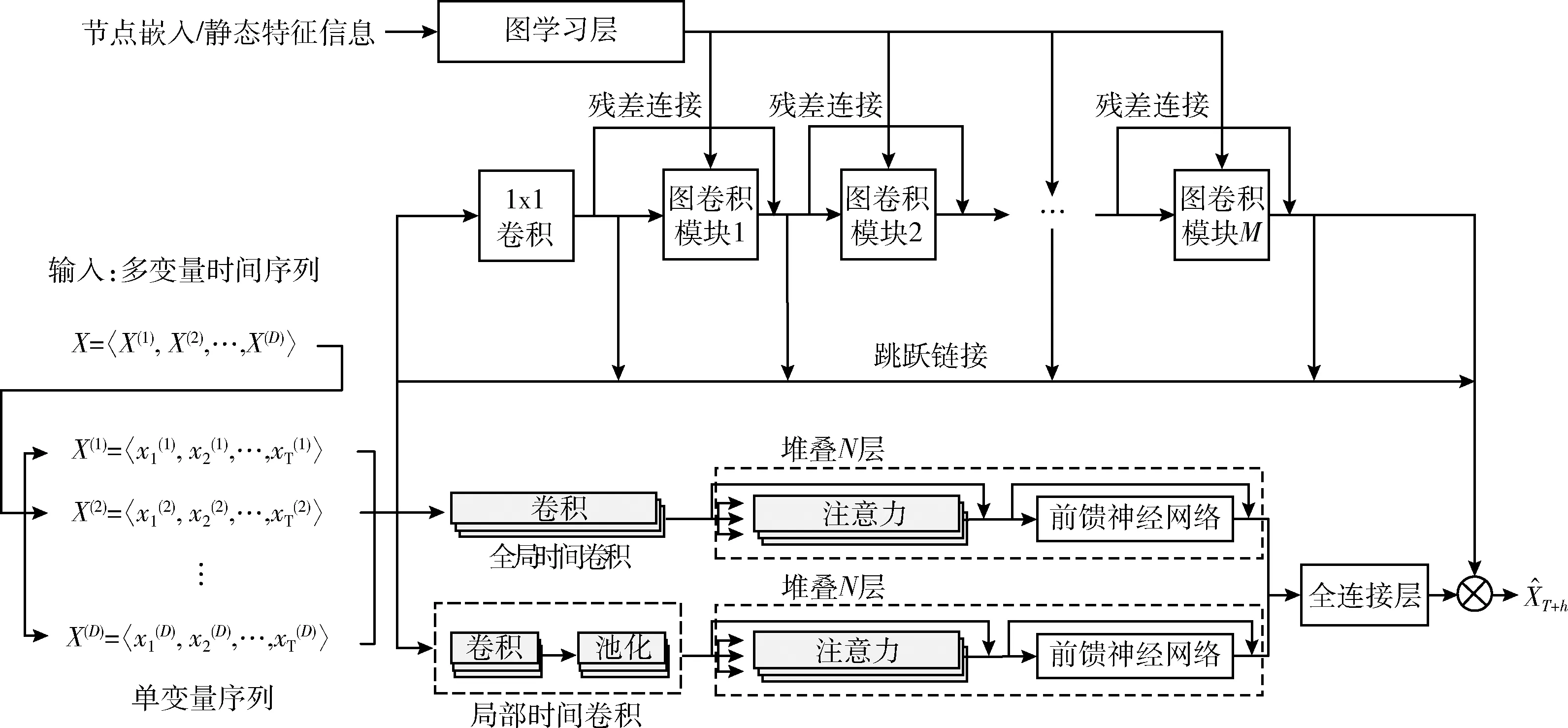
图1 基于注意力机制的CNN-GCN模型的整体框架结构
3.2 图学习层模块
DSAGCN采用图学习层自适应地学习对应于MTS样本的邻接矩阵[8],以图的形式学习MTS各变量时间序列之间隐藏的空间依赖关系。该模块可以学习MTS各变量之间的单向依赖关系,能更好适用于MTS的预测任务。具体学习方法如式(4)~式(6)所示
M1=tanh(αE1Θ1)
(1)
M2=tanh(αE2Θ2)
(2)
A=ReLU(tanh(α(M1M2T-M2M1T)))
(3)
fori=1,2,…,D
(4)

(5)
A[i,-idx]=0
(6)
其中,E1、E2表示随机初始化的节点嵌入,Θ1、Θ2为全连接网络的参数,用于随机初始化节点嵌入之间的依赖权重大小,Θ1、Θ2会随着训练的进行而学习到适合的权重以拟合MTS变量之间的空间依赖关系,α是控制激活函数饱和率的超参数。式(3)通过每个节点对之间正向依赖与反向依赖相减,将依赖关系转化为非对称性依赖,最终通过ReLU激活函数对邻接矩阵进行正则化。最后对于每个节点,选择它的top-k最近的节点作为它的邻居,在保留连接节点的权重的同时,将非连接节点的权重设置为零。
3.3 图卷积模块
图卷积模块按3.2节图学习模块生成的邻接矩阵,以卷积的方式实现多维时间序列中具有空间依赖性的变量之间的特征聚合。图卷积模块由两个混合跳传播层组成,分别处理通过每个节点的流入和流出信息。通过添加两个混合跳传播层的输出来获得单向流入信息。图2显示了图卷积模块和混合跳传播层的网络结构[8]。图2(a)中的T′表示邻接矩阵A转置。
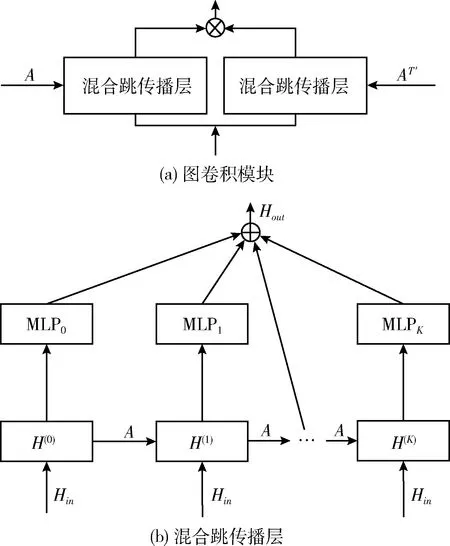
图2 图卷积和混合跳传播层
图2(b)为混合跳传播层的网络结构。图中A表示图学习模块学习得到的邻接矩阵,Hin为图卷积网络模块上一层的输出,混合跳图卷积的信息传播和选择过程按式(7)、式(8)进行
(7)
(8)
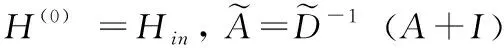
3.4 全局时间卷积模块
相比于RNN的迭代性和顺序性,卷积结构已经被证明在捕获特征和并行计算方面的能力,可以提升对于长序列的计算速度和预测效果,DSAGCN采用全局时间卷积模块用于提取MTS单变量时间序列所有时间步的时序特征[7]。具体卷积计算方式如式(9)所示
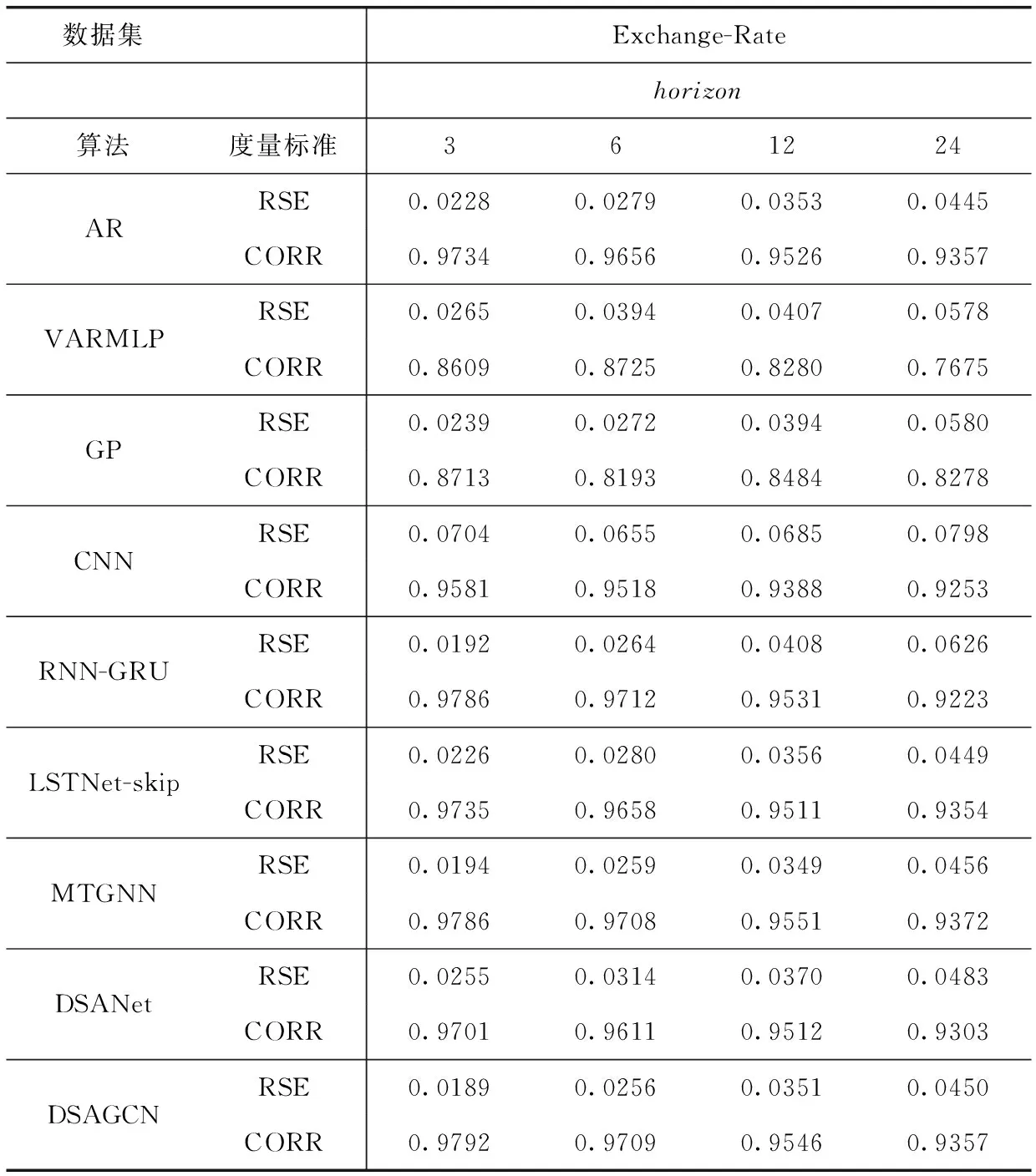
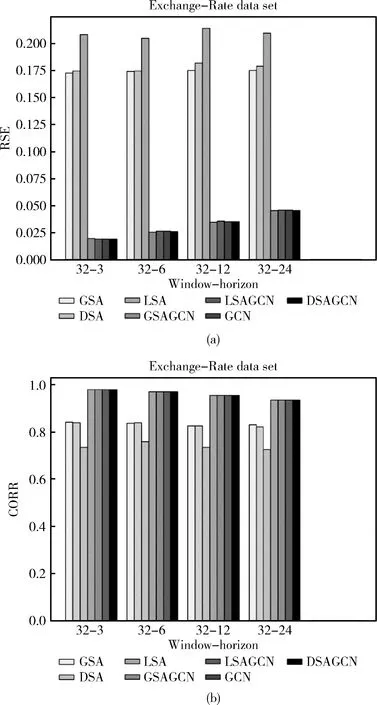
HG=RELU(Wk*X+bk) (0 (9) 式中:*表示卷积运算,Wk为第k个卷积核,文中用nG个T*1大小的卷积核对输入时间序列样本X∈RD*T进行全局卷积。那么D维的时间序列样本X由卷积运算生成一个D*1的向量。输入样本X由nG个卷积核得到一个大小为D*nG的输出矩阵HG。HG中每行中的元素表示不同权重的卷积核提取的不同属性的特征。 与全局时间卷积提取MTS各序列的固定时态特征,局部卷积侧重于建模MTS序列内部的局部时态模式[7]。文中局部时间卷积模块使用长度为l的卷积核进行卷积运算,以提取MTS序列内部局部上下文信息。对MTS样本X的第i维序列X(i)进行一次步长为s的类似式(9)的卷积操作,生成长度为Out=(T-L)/s+1嵌入向量。X的局部时间卷积结果生成矩阵MkL∈RD*o ut, 然后使用最大池化操作捕获MkL中最突出的特征。X的最终局部时间卷积运算结果为D维向量。和全局卷积模块相同,每个样本X由nL个卷积核生成表达局部时态信息的特征矩阵HL∈RD*nL。 文中还采用了自注意力机制进一步捕获MTS样本中各序列间的空间依赖关系[7]。该模块计算了3.4节和3.5节中全局时间卷积模块和局部时间卷积模块的输出矩阵HG和HL各行之间的注意力大小。下面具体说明全局时间卷积模块输出矩阵HG的各行之间注意力计算过程。 HG中的每一行记为X′,由式(10)~式(12)生成X′的查询、键和值矩阵QG、KG和VG。由式(13)计算HG各行之间的注意力得分。dκ是键的维数 QG=WQ*X′ (10) KG=WK*X′ (11) VG=WV*X′ (12) (13) (14) 位置前馈层由两个线性变换组成,在其间有一个ReLU作为激活函数,可以表示为 (15) 类似的,对于局部时间卷积后的自注意力模块与上述计算过程相同,HL经文中自注意力模块后的输出记为FL。 (16) (17) 模型的评估指标采用文献[6]使用的相对平方根误差(toot telative squared error,RSE、RRSE)和经验相关系数(empirical correlation coefficient,CORR)两个传统评估指标。这两个评估指标可以用公式如下表示 (18) (19) 汇率(Exchange-Rate)数据集:收集澳大利亚、英国、加拿大、瑞士、中国、日本、新西兰和新加坡等8个国家从1990年到2016年不等的每日汇率数据。 在本文进行的实验中,数据集按时间顺序分为训练集(60%)、验证集(20%)和测试集(20%)。在每一组中,使用滑动窗口将数据进一步分割成多个情况,这意味着在每一段中,使用T长度的多变量时间序列作为模型的输入数据,并使用在T+h时间戳的数据作为真实数据。 实验主要考虑了8个基线模型方法:AR、VARMLP、GP、CNN、RNN-GRU、DSANet、MTGNN、LSTNet-skip。而这些方法在引言中均已涉及提到。LSTNet-skip是文献[6]提出的一种融合了循环跳跃连接模块的LSTNet模型。 本文涉及的神经网络模型都是通过使用Adam优化器[17]执行小批量随机梯度下降(mini-batch SGD)来优化的。根据文献[8]设置进行实验的窗体大小(window size)为32,学习率为0.0001,梯度裁剪(clip gradient)为5,权重衰减率为0.000 01,训练步长为100,图学习层模块中的超参数α=3,图卷积模块数M=5,每个图卷积模块的层数为2,图卷积层模块中的超参数β=0.05,全局时间卷积的卷积核为(32,1),局部时间卷积的卷积核为(3,1),池化为最大池化,自注意力堆叠层数N=6,回归损失函数采用L1Loss即平均绝对误差L1损失。其它基线模型的参数设置依据原论文的参数设置。 本文涉及的模型方法均是在python3.7.6中实现的,其中深度学习方法是在Py-Torch1.2.0版本上实现的,所有实验均是使用配置英特尔i7-7700CPU、8核、16 GB RAM、NVIDIA Quadro P2000的机器运行的。 表1概括总结了在国际汇率数据集上实验涉及到的所有9个模型方法在RSE和CORR两个评价标准上的评估结果。分别设置horizon={3,6,12,24}, 即设置horizon从3天到24天不等用于预测。从进行的实验情况可以看出horizon越大,对任务进行预测就越难。在horizon=3、6时本文提出的DSAGCN模型的预测效果最好,说明预测步长较小时,DSAGCN模型能够较好提取和利用时空依赖关系特征来提高预测效果。当horizon=12、24时AR模型和MTGNN模型预测效果较好,表明预测步长较大时,DSAGCN模型就不如AR模型和MTGNN模型的预测效果了,但预测精度差别不大。从总体性能上来说本文提出的DSAGCN模型在所用实验数据集上的预测性能是优于其它基线模型的。 图3展示了消融实验各模型情况。GSA(global self-attention network)表示只有全局时间自注意力一个通道的模型,LSA(local self-attention network)表示只有局部时间自注意力一个通道的模型,GCN表示只有一个图卷积通道的模型(当然也有图学习模块),DSA(dual self-attention network without AR)表示有全局时间自注意力和局部时间自注意力两个通道的模型,GSAGCN(global self-attention and graph convolutional network)表示有全局时间自注意力和图卷积两个通道的模型,LSAGCN(local self-attention and graph convolutional network)表示有局部时间自注意力和图卷积两个通道的模型,DSAGCN表示本文提出的三通道模型。 从图3(a)可以看出LSA模型的RSE值最大;DSA和GSA两模型的RSE值依次较大;GSAGCN、LSAGCN、GCN和DSAGCN这4个模型的RSE值较小,而这4个模型是都含有GCN模块或者说GCN通道的。 表1 不同模型在数据集上的单步预测实验情况 图3 消融实验情况 从图3(b)可以看出LSA模型的CORR值最小;DSA和GSA两模型的CORR值较小;GSAGCN、LSAGCN、GCN和DSAGCN这4个含有GCN模块的模型的CORR值较大。RSE值越小,CORR越大,则说明模型越好。从消融实验的结果图3(a)、图3(b)可以分析出:含有GCN模块的4个模型均较好,所以说GCN通道对模型预测精度的贡献较大,能够很大程度上影响模型的好坏。说明GCN通道所采用的图学习层模块能够通过很好地自适应地学习图数据的邻接矩阵,来捕获时间序列数据之间隐藏的空间依赖关系,图卷积层模块通过图卷积操作很好地处理了图学习层模块学习到的图中的空间依赖关系。在GCN通道上再加入另外两个通道,模型性能又有了一定程度提高,说明全局自注意力通道和局部自注意力通道提取到的特征信息可以在一定程度上提高本文提出的DSAGCN模型方法的预测精度。所以说3个通道对模型的预测精度均有贡献,均能一定程度上提高模型的预测精度。 本文提出了基于深度学习的一种多变量时间序列预测模型DSAGCN。DSAGCN利用图卷积神经网络GCN提取多变量时间序列变量之间的空间依赖关系特征,利用卷积神经网络CNN和注意力机制提取多变量时间序列的前后长短期时间片段的时间依赖关系特征,然后融合多变量时间序列的时间和空间依赖关系特征进行预测。在国际汇率(Exchange-Rate)数据集上进行应用的实验结果表明本文提出的模型在各方面的综合性能是优于本文提及的基于深度学习的其它基线模型的。DSAGCN模型可以在交通流预测、农业劳动力供给预测、网络舆情预测、商品销售量预测等等具体的领域中做进一步应用。3.5 局部时间卷积模块
3.6 自注意力模块

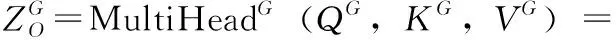
3.7 预测结果的输出
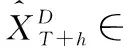
4 实验及结果
4.1 评价标准
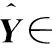
4.2 实验数据介绍
4.3 实验详述
4.4 实验结果及分析
5 结束语
