基于谱聚类的社交网络差分隐私保护算法研究*

2022-03-22晏飞扬文志云张振康

计算机工程与科学 2022年2期

袁泉，晏飞扬，文志云，张振康

(1.重庆邮电大学通信与信息工程学院,重庆 400065；2.重庆邮电大学通信新技术应用研究中心，重庆 400065；3.重庆信科设计有限公司，重庆 401121)

1 引言

在大数据时代的各种社交网络应用所产生的网络数据中，蕴含着大量用户的隐私数据，如果不对这些数据加以保护，用户的隐私信息将极易被窃取，造成难以估量的损失。如2018年发生的Facebook“泄密门”事件，导致5 000多万用户的个人信息被数据分析公司用于分析和干预选民的投票意向。该事件被曝光后，掀起巨大的舆论风波，同时也再一次凸显出个人的数据隐私保护面临着巨大的挑战[1]。

在保护隐私数据的方法中，差分隐私保护方法[2]通过一种严格的数学模型，可有效防止攻击者在拥有背景知识的前提下对数据进行差分攻击。但是，传统的权重社交网络差分隐私保护方法还存在以下问题：

(1)直接对边权重添加噪声扰动，会导致添加的噪声量过大，从而使得数据可用性急剧下降，该举措虽然提高了数据安全性却降低了可用性；

(2)因使用统一的隐私预算参数ε，使得不同权重的边添加的噪声量一致，造成了隐私保护不均衡问题。

本文针对上述权重社交网络隐私保护存在的问题，提出了一种基于谱聚类的差分隐私保护算法SCDP(Differential Privacy protection based on Spectral Clustering)，该算法可在减少噪声添加量的同时均衡隐私保护程度，提高经过隐私保护算法处理后的数据可用性。

2 相关工作及基本概念

2.1 相关工作

在隐私保护领域，许多学者对社交网络差分隐私保护、个性化差分隐私保护和直方图发布差分隐私保护等方面进行了研究。其中，兰丽辉等[3]设计了一种基于差分隐私模型的LWSPA(Less Weighted Social Privacy Algorithm)算法，实现了边权重的强保护。但是，直接添加噪声的方式使得数据可用性下降。Li等[4]提出了合并桶和一致性推理策略来保护加权社交网络图。Huang等[5]在差分隐私模型的基础上，结合聚类和随机化算法，提出了一种差分隐私保护算法PBCN(Privacy preserving approach Based on Clustering and Noise)。该方法有效提高了处理后的数据可用性。Qin等[6]则提出了基于用户与整个人群不同分区之间的联系来逐步聚集用户的LDPGen(Local Differential Privacy Generation)模型，该模型采用现有的社交网络图生成模型来构建综合社交网络图。这些方法均使用统一的隐私预算参数ε，导致隐私保护程度不够均衡。在个性化隐私保护领域，Chen等[7]提出的发布差分私有综合属性图的方法能够在不以牺牲原始图全局结构属性为代价的同时保留原始图的社团结构。在Sun等[8]制定的差分隐私方案中，要求每个参与者不仅考虑自己的隐私，还需考虑与其有关联的邻居的隐私。针对直方图隐私发布问题，Qian等[9]提出了2种基于序列感知和局部密度的聚类方法来聚集直方图，通过加权图的权分布来研究发布拓扑信息的问题。这些方法依然存在数据可用性低、隐私保护不均衡等问题。

2.2 基本概念

(1)权重社交网络。

设无向权重图G=(V，E，W) 是一个表示权重社交网络的三元组，其中V={v1,v2,…,vn}表示图G中n个节点的集合，E={e=(vi,vj)|vi,vj∈V,i≠j}表示图G中n个节点间边的集合，W表示边权重值的集合。在对数据处理时，权重社交网络图可以用邻接矩阵来表示。

(2)谱聚类。

谱聚类算法将聚类问题转化为图的最佳分割问题[10]。相比传统的k-means聚类算法，谱聚类具有更高效、聚类效果更均匀的优点。根据不同的准则函数和谱映射方法，谱聚类算法有很多不同的具体实现方法，但都可以归纳为以下4个主要步骤：

步骤1构建相似度矩阵T；

步骤2构建度矩阵D，求出拉普拉斯矩阵L；

步骤3计算L的前l个特征向量；

步骤4通过一些经典聚类算法对特征向量进行聚类。

本文利用谱聚类算法更高效、聚类效果更均匀的特点，将其用作SCDP算法中处理社交网络图聚类的算法，目的是提高算法效率和数据可用性。

定义1(相似度矩阵T) 权重wij为T第i行第j列对应的值。wij使用全连接法来构建,本文使用高斯核函数定义边权重。如式(1)所示：

(1)

其中，σ为高斯核函数的尺度参数。

则相似度矩阵T如式(2)所示：

(2)

定义2(度矩阵D) 无向权重图中任意一点vi的度di的定义如式(3)所示：

(3)

则度矩阵D如式(4)所示：

(4)

定义3(拉普拉斯矩阵L) 拉普拉斯矩阵是谱聚类算法的重要工具，其计算方法如式(5)所示：

L=D-T

(5)

本文通过谱聚类算法将较大的权重社交网络图聚类形成不同的簇，再对聚类后具有相似特征的簇进行随机噪声添加，通过这样的噪声添加方式，能够减少添加的噪声，有效提高数据的可用性。

(3)ε-差分隐私模型。

定义4(差分隐私) 假设存在随机算法K，对于任意2个邻近数据集D和D′，若算法K满足ε-差分隐私保护，用range(K)表示K的取值范围，则对于所有的S∈range(K)，有：

P[K(D)∈S]≤exp(ε)×P[K(D′)∈S]

(6)

其中，P[E]表示事件E的泄露概率，其值与随机算法K相关;ε表示差分隐私预算，决定了噪声添加量,ε越小，噪声添加量越大。

定义5(全局敏感度) 对于任意函数q:D→Rd，q的全局敏感度(简称为敏感度)定义如式(7)所示：

(7)

其中，D表示输入数据集，D与D′为邻近数据集，至多相差一条记录即至多有一条边不同。本文将全局敏感度设为Δq=Wmax，Wmax为差异边最大差异权重值。d表示输出实数向量的维度。

定义6(拉普拉斯机制) 给定数据集D，设有敏感度为Δq的函数q:D→Rd，若随机算法K的输出满足：

K(D)=q(D)+Lap(Δq/ε)

(8)

则称算法K满足ε-差分隐私保护。差分隐私添加噪声的大小跟ε成反比，簇中节点间的边权重越大，理论上需要更强的保护，因此应该分配的ε值越小。由于全局的ε值不统一，本文使用组合差分隐私策略。

定义7(组合差分隐私) 已知数据集D={c1,c2,…,ci},D′={c′1,c′2,…,c′i}，给定隐私算法K，D和D′中都包含有i个簇，相对应的簇ci和c′i只相差一条记录边，每个簇的ε值不同。range(K)表示K的取值范围，若K在ci和c′i上的任意输出结果Ci(Ci∈range(K))满足不等式P[K(ci)∈Ci]≤eεiP[K(c′i)∈Ci]，则称K满足组合差分隐私，如式(9)所示：

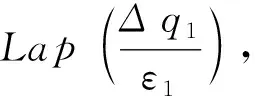
(9)

其中,εi是簇ci对应的隐私预算，Lap(Δqi/εi)是为ci生成的Laplace噪声。

3 基于谱聚类的权重社交网络差分隐私保护算法

3.1 基本思想

权重社交网络隐私保护面临着隐私保护不均衡、噪声添加量过大等问题。针对这些问题，本文在差分隐私模型的基础上，结合经典的谱聚类算法，将权重社交网络图聚类成为拥有相似特征的不同的簇，再以Si为抽样频率向簇中的边权重随机添加拉普拉斯噪声，以达到减少噪声添加量的目的，进而提高数据的可用性。同时，本文算法设计了新的隐私预算参数ε′，使得噪声添加更加均衡。再利用差分隐私模型中的组合定律证明所提算法满足ε-差分隐私模型。

3.2 抽样频率Si

传统的差分隐私保护对权重社交网络直接添加拉普拉斯噪声会造成噪声添加量过大，数据可用性将会降低，为了尽可能地提高数据的可用性，本文提出的SCDP算法将采用随机添加噪声的方式，以Si为抽样频率，对聚类后网络边权重添加噪声。Si的定义如式(10)所示：

Si=簇边向量总数/边向量总数

(10)

3.3 差分隐私预算ε′

针对权重社交网络，添加噪声时边权重越大表示节点之间的关系越紧密，说明该边需要强保护，需将隐私预算参数设定为一个较小的值。反之，隐私预算参数设定为一个较大的值。因此，在本文提出的SCDP算法中，为了提高隐私保护的均衡性，进而提高数据可用性，将隐私预算参数设计为ε′。ε′的定义如式(11)所示：

(11)

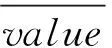
3.4 SCDP算法基本流程

本文所提出的SCDP算法的基本流程如算法1所示。

算法1SCDP算法

输入：原始权重社交网络图G，初始隐私保护预算ε，聚类系数k。

输出：隐私保护后的权重社交网络图G*。

步骤1计算n×n的相似度矩阵T;

步骤2计算度矩阵D;

步骤3计算拉普拉斯矩阵Lrw=D-1L=D-1(D-T);

步骤4计算Lrw的特征值，将特征值排序，取前l个特征值，并计算前l个特征值的特征向量u1,u2,…,ul;

步骤5由步骤4的l个列向量组成矩阵U={u1,u2,…,ul};

步骤6令yi∈Rk为U的第i行向量，其中i=1,2,…,n;

步骤7使用k-means算法将新样本点Y={y1,y2,…,yn}聚类成簇C1,C2,…,Ck;

步骤8将C={C1,C2,…,Ck}中每个簇的节点和边权重信息构成三元组(i，j，x)，把所有簇间的边的三元组单独记录下来，i、j是节点编号，x代表权重，当节点之间无连接时，x设置为0;

步骤9根据每个簇的三元组信息生成边向量X=[X1,X2,…,Xk]，其中簇的边权重集合表示为Xi={x1,x2,…,xi(i-1)/2};

步骤10根据每个簇的边权重信息，得到k个簇的隐私预算ε′={ε′1,ε′2,…,ε′k};

步骤11对X以Si为频率进行随机抽样，根据每个簇的ε′k值，生成拉普拉斯噪声Lap=Lap(Δqk/ε′k);

步骤12为每个簇构造服从Laplace分布的向量组〈Lap(Δqk/ε′k)〉X;

步骤13生成满足ε-差分隐私的簇向量组P=X+〈Lap(Δqk/ε′k)〉X;

步骤14生成满足ε-差分隐私的权重社交网络图G*={P1,P2,…,Pk};

步骤15输出隐私保护后权重社交网络图G*。

3.5 算法的隐私性分析

由于每个簇使用的隐私预算ε′不同，无法直接对全局的隐私性进行分析。因此，本文通过差分隐私中的组合定律来进行间接分析。根据定义7给出的组合差分隐私需要满足的不等式来分析算法的隐私性。如果所有的簇都满足ε-差分隐私，则全局也满足ε-差分隐私。

设G和G*只相差一条边，隐私算法为K，range(K)表示K的取值范围，若K在G和G*上的任意输出结果M(M⊂range(K))满足不等式P[K(G)∈M]≤eεkP[K(G*)∈M]，则本文隐私算法K满足ε-差分隐私。

证明设m∈M，M与X维度相同，设其维度为X，由条件概率知：

(12)

其中,K(G)=m表示算法K在G上的输出结果为m，σ=Δqi/ε′i是服从Laplace分布的尺度参数，由定义5可知，Δqi=Wmax。得：

(13)

由K(G)-K(G*)≤Wmax知，

(14)

□

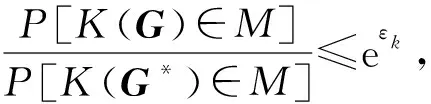
4 实验与结果分析

4.1 实验设置

实验数据如表1所示。其中，Lesmis[11]是带权社交网络图，Football[12]是无权图，利用随机数生成器为其随机生成[1，20]的整数作为无权图中边的权重值。

Table 1 Experimental data

4.2 实验结果分析

在参数的选取上，本文选择了算法执行时间，以及常用于反映网络特征的平均聚类系数和平均最短路径作为测试SCDP算法数据可用性的参数。将算法处理后的参数与原始网络参数进行对比，若结果与原始网络参数越接近则说明算法处理后的数据可用性越高。

为验证本文所提算法对社交网络隐私保护的改进，实验选取不同聚类系数k值下的SCDP算法与直接添加Laplace噪声的传统社交网络差分隐私保护算法的执行时间进行对比。为验证本文算法的有效性，实验选取不同聚类系数k值下的SCDP算法、LWSPA算法[3]和PBCN[5]算法进行对比，主要比较3种算法在平均聚类系数和平均最短路径2个方面的表现。实验均在Lesmis和Football网络数据集上进行。其实验结果分别如图1～图3所示。

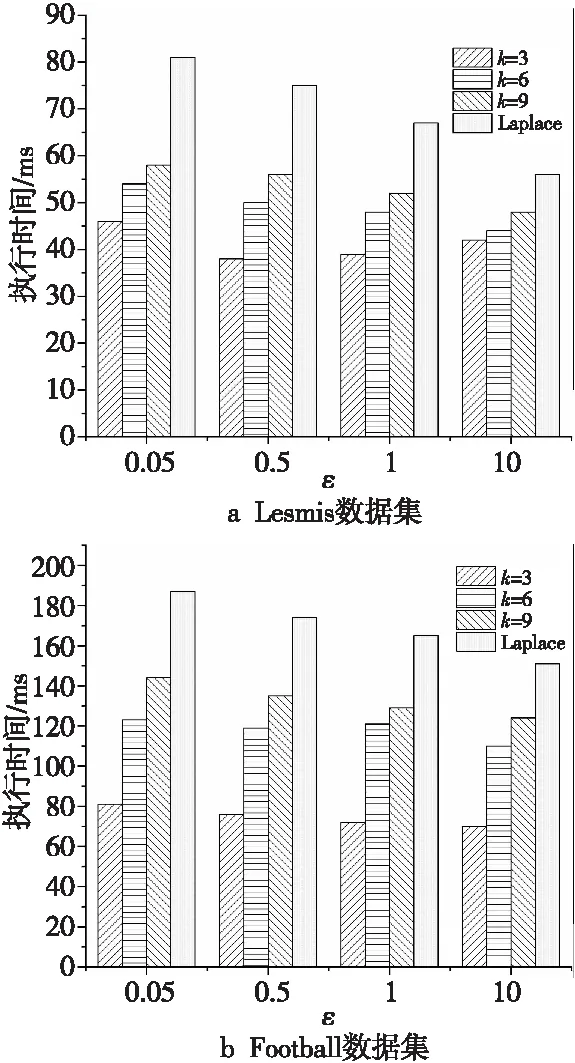
Figure 1 Comparison of execution time 图1 执行时间对比

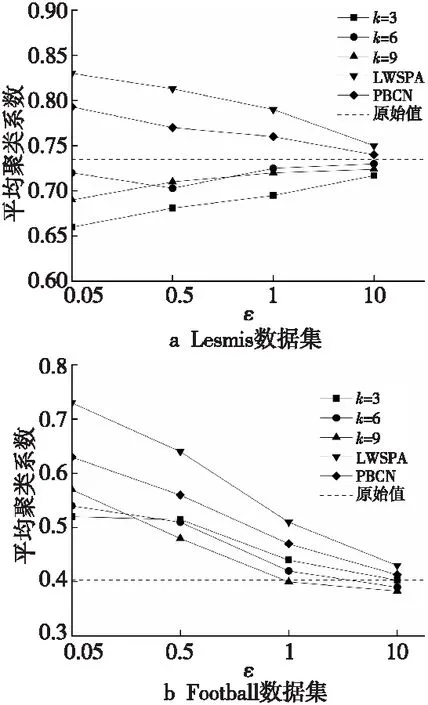
Figure 2 Comparison of average clustering coefficient图2 平均聚类系数对比

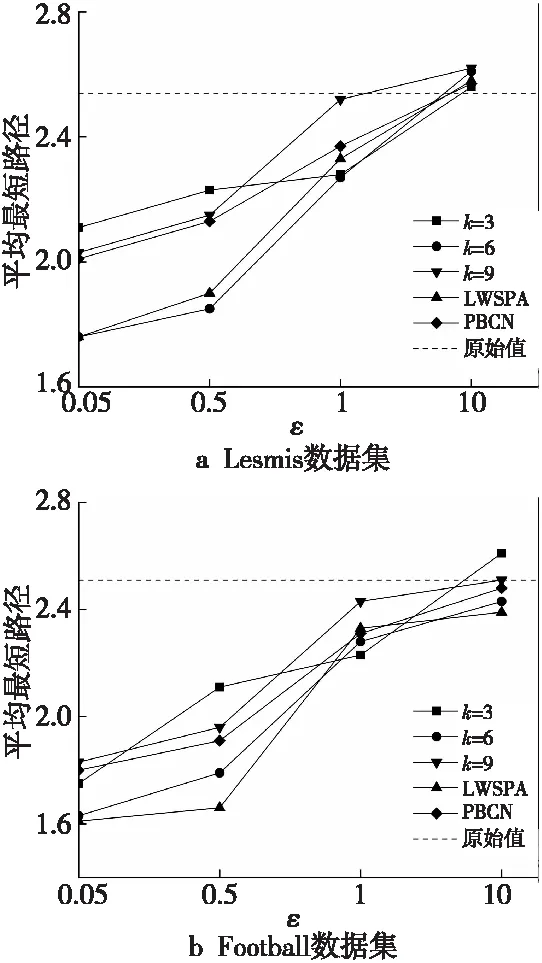
Figure 3 Comparison of average shortest path图3 平均最短路径对比

由图1可知，随着聚类系数k值的增大，SCDP算法与直接添加Laplace噪声的传统算法的执行时间均随之增加。但是，SCDP算法的执行时间明显少于传统算法，算法执行效率更高。因此，可以证明本文所提的算法提高了社交网络差分隐私保护的效率。

由图2可知，随着隐私预算ε增大，SCDP算法与对比算法LWSPA、PBCN的实验结果均逐渐呈现接近原始值的趋势，数据可用性逐渐提高。当k值为6,9时，由于本文提出的SCDP算法随着ε值的增大，添加的噪声量更少，使得数据的可用性提高，SCDP算法的平均聚类系数更接近原始值，因此表现优于LWSPA和PBCN算法。

由图3可知，随着ε值的增大，噪声的添加量下降，SCDP算法与对比算法均呈现出与原始值逐渐接近的趋势。当k值为3时，因聚类数目较少，SCDP算法在聚类时的效果不佳，导致SCDP算法比LWSPA、PBCN表现较差。当k值为6,9时，SCDP算法的平均最短路径值更加接近原始值，数据可用性高于对比算法。此时聚类划分更多，聚类效果提升。并且，随着ε值的增大，随机添加的噪声量下降，而新的隐私预算参数使得噪声添加更加均衡，因此SCDP算法的表现优于对比算法LWSPA和PBCN。这证明了本文算法的有效性。