面向大规模图计算的连通分量算法分析与优化*
2022-03-22甘新标杨文祥贾孟涵涂旭平张一鸣朱春平
白 皓,甘新标,杨文祥,贾孟涵,涂旭平,张一鸣,郭 敏,来 乐,张 意,朱春平
(1.国防科技大学计算机学院,湖南 长沙 410073;2.中国空气动力研究与发展中心计算空气动力研究所,四川 绵阳 621000;3.黄冈师范学院计算机学院,湖北 黄冈 438000;4.中国人民解放军66061部队,北京 100144)
1 引言
图作为一种常见的数据结构,可以用来抽象表达现实事物间各种复杂的关联关系[1]。例如,社交网络、万维网等可以采用图表示。近年来,图数据的规模不断增长,根据相关报告显示,2021年第一季度,Facebook每月活跃用户为2.85亿[2],腾讯WeChat月活跃用户达到1.24亿[3],把用户和其之间的关系抽象为图中的节点和边,那么图中节点的规模达到了数十亿,边的规模更是达到了数千亿。图计算是针对图数据进行处理和计算,在现实生活的诸多场景中都发挥着重要作用。
从图中某一节点出发访遍图中其余节点,且每个节点仅被访问一次,这一过程叫做图的遍历。无向图的连通分量,也叫极大连通子图,指的是每对节点都能通过通路来互相连通的子图。连通分量算法通过某种方式来求解图中的连通分量,可以应用于可达性查询、一致性检测等众多场景,通常是大规模图处理的重要步骤[4]。对连通图进行遍历过程中所经过的边和节点的组合称为生成树。非连通图可分解为多个连通分量,而每个连通分量又各自对应至少一棵生成树,面向超级计算机的大规模图计算Graph500[5]测试的目的就是通过大规模图计算遍历找到一棵最小生成树。
如果在连通分量上进行遍历运算,得到对应于该连通分量的生成树,就是极大连通子图的极小连通子图,这样,只需要在每个连通分量中选定一个节点作为根节点就可以把整个连通分量遍历完,连通分量中的其他节点不需要再做遍历算法根节点的尝试,可见依靠连通分量可以帮助减少一些不必要的遍历开销。在并行计算环境下,在点划分时把同一个连通分量中的节点划分到逻辑中相近的物理节点上,可以实现负载均衡,降低通信开销,加快生成树的生成。因此,求解非连通无向图的连通分量成为了加速大规模图遍历的重要方法。
在单处理器上,Hopcroft等人[6]使用深度优先搜索DFS(Depth First Search)来求解连通分量,其时间复杂度为O(m+n),m和n分别是图中边和节点的数量。然而这种方法很难并行实现[7]。Hirschberg等人[8 - 10]分别用不同数量级的处理器实现了O(log2n)的时间复杂度。van Scoy等人[11,12]分别提出了时间复杂度为O(n)的并行处理方法。Chen等人[13]提出了一种基于k步上近似的粗糙集算法来求解连通分量,进一步优化了性能。Pedroche等人[14]利用RCM(Reverse Cuthill-McKee)方法实现了时间复杂度为O(m+n)的算法。Kofman等人[15]在特定条件下在基于集合的无向图中实现了常数级的计算开销。孙斌[16]对串行算法和多个典型的并行算法进行了比较。Zhang等人[17]提出了性能和扩展性较好的FastSV(Fast Shiloach-Vishkin)算法。Liu等人[18]在PRAM(Parameter Random Access Memory)上实现了时间复杂度为O(logd+log logm/nn)的算法,其中,最大连通分量直径为d,这为在超算平台上运行连通分量算法提供了借鉴。Bentert等人[19]基于无线传感器网络对连通分量算法进行了讨论。Durgut等人[20]则利用连通分量算法对求解网络通信中图的破裂程度进行了优化。上述研究将连通分量算法应用于网络通信,把网络问题抽象为寻找生成树或最短路径问题,根本目的是为了减少不必要的访问,实现系统的最低能耗。
无向图连通分量的基础方法主要有3种:BFS(Breadth First Search)、DFS和并查集算法(Union-Find Algorithm)[21,22]。前两者都是遍历算法,通过遍历图中所有的节点,得到独立的子图,即连通分量。并查集算法是通过指定某一连通分量中的唯一根节点,然后不断添加新的连通信息,从而找到连通分量。
本文围绕连通分量算法,着重研究了算法和数据结构的性能等问题,主要有以下贡献:
(1)对并查集算法和数据结构进行配合度分析,提出捷径向量算法。
(2)单线程与多线程相结合,利用迭代轮转对算法进行并行优化。
(3)全面分析比较了BFS、DFS和并查集算法对无向图连通分量算法的实现性能和应用场景。
2 连通分量算法
广度优先搜索、深度优先搜索和并查集算法都可实现无向图连通分量算法,其中广度优先搜索和深度优先搜索都是利用遍历的思想对所有相连的节点进行搜索访问,当以邻接矩阵作为图的存储结构时,其算法复杂度均为O(n2)。并查集算法是通过合并具有等价关系的节点对(即一条边),来找到所有的连通分量,其传统方法实现的时间复杂度是O(fu),其中f是下文中Find的次数,u是Union的次数。
2.1 用遍历算法寻找连通分量
BFS算法初始时把所有节点都加载到内存,并遍历这些节点,每访问到一个节点,如果其未被访问过,就以其为根节点执行BFS算法,这样每次执行BFS算法都会得到一个连通分量。
DFS算法与之类似,所不同的是遍历过程采用的是DFS算法。
2.2 用并查集算法寻找连通分量
并查集算法在初始状态时,每个节点的根节点均设置为自身,建立指向自身的指针,自成一棵树,如图 1所示。在扫描边进行迭代的过程中,如果2个节点的指针未指向同一个节点,则改变指针,将2个节点置于同一棵树中。
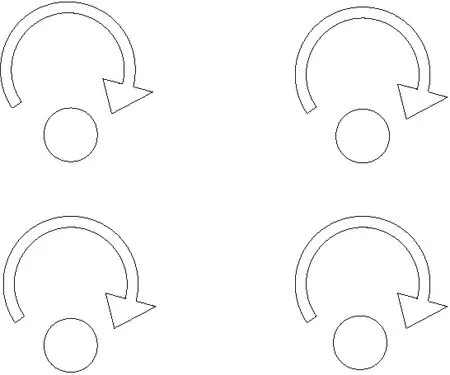
Figure 1 Initial state of Union-Find Algorithm图1 并查集算法初始状态
该算法主要有2个基本数据操作:(1)查找(Find):确定节点属于哪一棵树,用来确定2个节点是否处于同一棵树,如图 2所示,双箭头表示扫描到的边,黑色连接线表示在树中节点的父子关系,虚线箭头表示寻找根节点的过程。(2)合并(Union):如果一条边的2个节点不属于同一棵树,则将2个节点合并到一棵树中,如图 3所示。
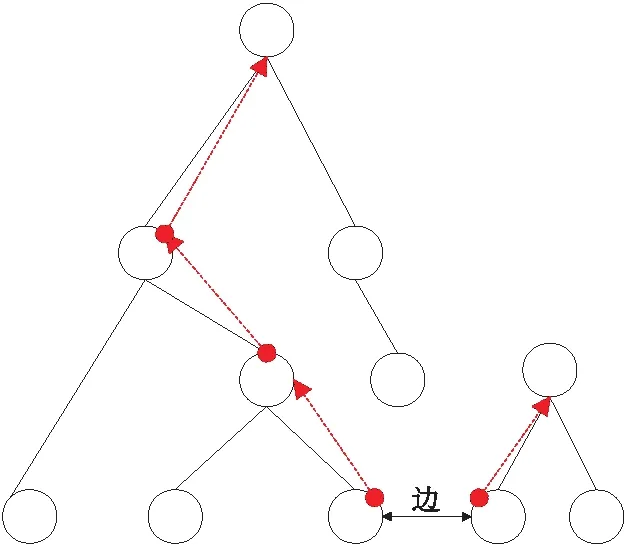
Figure 2 Operation of finding root node图2 查找根节点操作
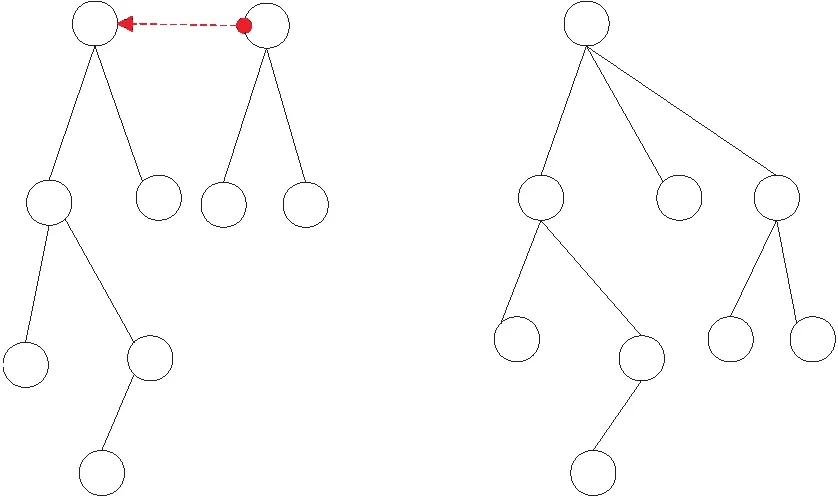
Figure 3 Operation of unioning tree图3 合并树操作
利用并查集实现的连通分量算法如算法1所示。
算法1利用并查集算法实现的连通分量算法
Input:edge.bin.//输入边数据集
Output:connectedcomponent.//输出连通分量
initialization;//初始化
functionfind(x);//定义find子函数
whileeinedge.bindo//遍历边数据集
//把出现的节点放入节点集合
vertexset.insert(e.v1);
vertexset.insert(e.v2);
end
whileeinedge.bindo//遍历边数据集
//寻找2个节点的根节点
xroot=find(e.v1);
yroot=find(e.v2);
/*如果2个节点的根节点不相同,则把一个的根节点置为另一个的子节点*/
ifxroot!=yrootthen
xroot.parent=yroot;
end
end
//输出连通分量
forvinvertexsetdo
ifson[v].size!=0then
output(connectedcomponent);
end
end
算法中,edge.bin表示从Graph500中生成的二进制边数据集,connectedcomponent指的是每个连通分量的基本信息,如包含的节点、边等,e是每次从数据集中读取的包含边信息的结构体,v1/v2表示构成边的2个节点,insert()就是节点载入内存的过程,find()用来查找节点的根节点,parent表示节点的父节点,son[v]表示以v节点为根节点的所有节点。
3 捷径向量算法
3.1 串行捷径向量算法
传统的并查集算法创建的树可能会不平衡,其优化算法主要有2种,第1种是“按秩合并”,把深度较小的树(即秩较小的树)连接到更大的树上,从而增加树的平衡性,如图 4所示。第2种是“捷径”(Shortcutting),让节点从指向父节点改成直接指向根节点,减小树的层级,如图 5所示。这2种方法避免了过多的find(·)函数的递归次数,在Graph500生成的节点规模为240数据集的条件下,每次递归都需要开辟资源来完成子函数的初始化,这无疑是巨大的开销,因此这2种优化是十分有必要的。这2种优化算法的时间复杂度均是O(kα(k,n)),其中,k表示合并查找的操作次数,n为节点数量,α(k,n)为反Ackermann函数[23 - 25]。
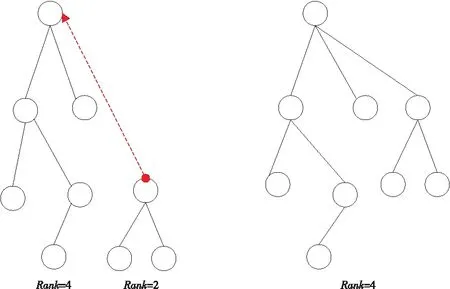
Figure 4 Union by rank图4 按秩合并
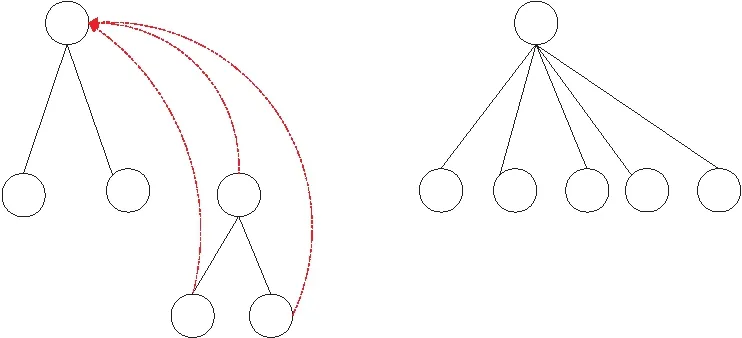
Figure 5 Shortcutting图5 捷径操作
虽然2个优化算法的时间复杂度一样,但如果结合数据结构考虑,性能会有差异。为了更好地结合算法和数据结构的优势,本文提出了捷径向量算法。
并查集算法需要建立一个数组来存储节点的根节点。此外,每棵树的根节点需要存储所有子节点即以自己为根的所有节点的信息,这就需要建立一个二维的数据结构,由于涉及节点的按下标随机访问,第1维采用向量。对第2维,集合具有排序和去重的开销,而算法的实现细节中并不需要这样的功能,故本文不考虑使用集合来实现。对比向量和链表的特点,向量的构造函数会把每个元素初始化一遍,访问时Cache的命中率较高,赋值和访问速度极快,插入则相对较慢,本文根据数据规模能够预估一些用向量表示的变量的大小,也避免了在向量插入过程中的扩大容量、拷贝内存和释放原有内存的操作。而链表虽然在按秩合并算法中只改变2个节点的指针,但其缺点也是比较明显的,一是遍历时需要用迭代器,访问迭代器需要进行迭代器越位、有效性、是否指向同一容器等方面的判断,开销较大;二是插入时需要改变指针,而向量在插入时虽然需要多次扩容,但这种开销对整体算法的加速是值得的。
从数据结构与算法结合来看,使用捷径向量算法时,需要把一棵树中所有节点的根节点都改换成另一棵树的根节点,这需要遍历访问,向量比链表快。按秩合并如果采用链表,在更新子节点信息时,只需要改变2个节点的指针,虽然在这方面比向量的遍历增加子节点要占优,但它在调用子函数find(·)时开辟的新资源比向量不使用子函数的情况要大得多,还需要存储标志秩大小的rank的结构。综合考虑,捷径向量算法省去了多次调用子函数的开销,性能表现会更好。
捷径向量算法的过程如图 6所示,在合并前,2棵树各自用二维向量来存储各自的信息,树根节点是向量最顶端的节点,尾部的箭头表示新插入节点元素的向量增长方向,当新访问到的边的2个节点分别属于2棵树时(边由双向箭头表示),一棵树所对应的向量被整体复制到另一棵树的向量尾部,沿增长方向依次插入,所以新加入节点元素的根节点指针均改换为指向目的树向量的根。
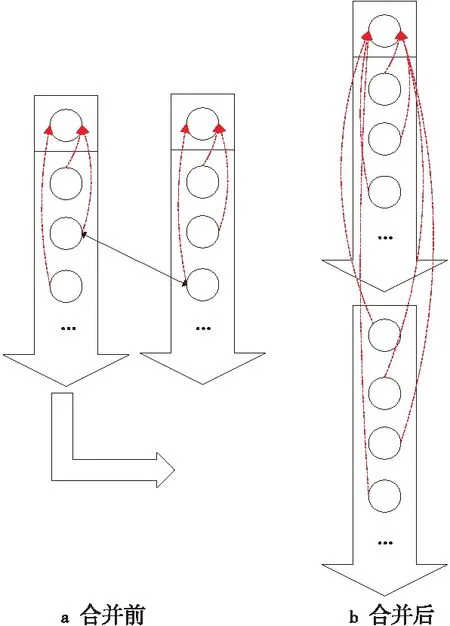
Figure 6 Shortcutting-vector algorithm图6 捷径向量算法
3.2 捷径向量算法与遍历算法比较
从时间复杂度来讲,并查集算法要更快。因此,如果只是为了求基本的连通分量的节点信息,而没有太多其他需求,就使用并查集算法来实现。
遍历算法的邻接表保存了边的信息,当建立连通分量的时候,可以很自然地把边的信息表示出来,但邻接表中存储了重复的信息,每一条边的2个节点都存储了对方的信息,造成了2倍的开销。而并查集算法在合并时忽略了边的信息,导致一部分信息的缺失。
在空间开销方面,遍历算法需要存储以下数据结构:邻接表、状态数组、正在处理的节点的队列或栈。在Graph500使用的Kronecker生成图中,默认的节点平均度数为16,设图中节点的数量为n,则邻接表包含了16n规模的整型数据,对应每个节点,建立一个长度与节点数量n相等的状态数组,还需要维护队列或栈的大小,其大小分别与BFS生成树的每层的节点数量或DFS生成树的层数有关。因此,遍历算法的空间复杂度为O(n),n表示节点数量,占用空间随着参数n的平均增加速率为16。
捷径向量算法需要存储以下数据结构:二维子节点向量和根节点数组。各个连通分量的根节点存储了属于自己的子节点信息,由于Kronecker生成图满足幂律分布的特点且该算法按照扩容因子为2的规则来设置子向量长度,故对节点数量为n的图,二维子节点向量占据的空间为2m,其中表示边数量的m满足如式(1)所示的关系:
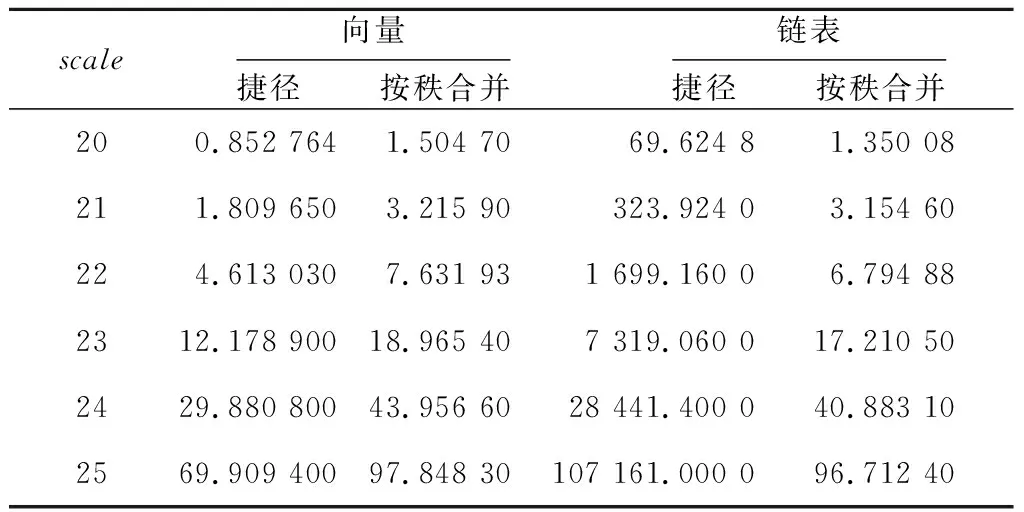
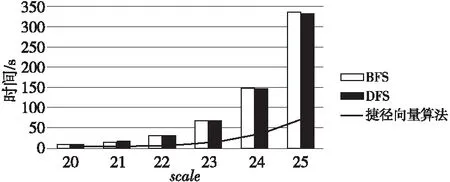
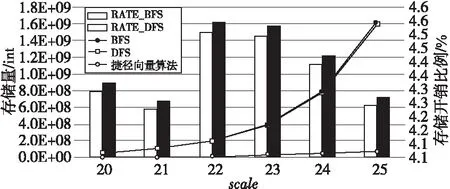
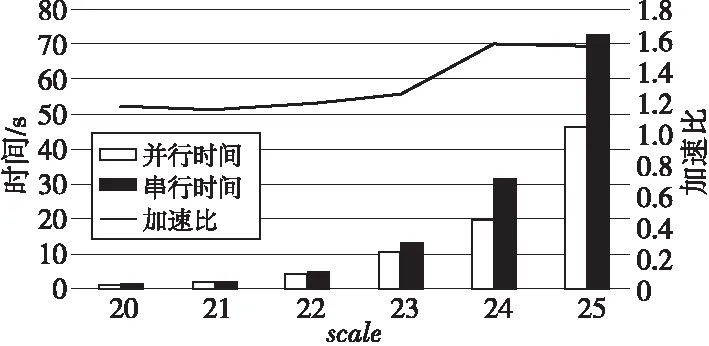
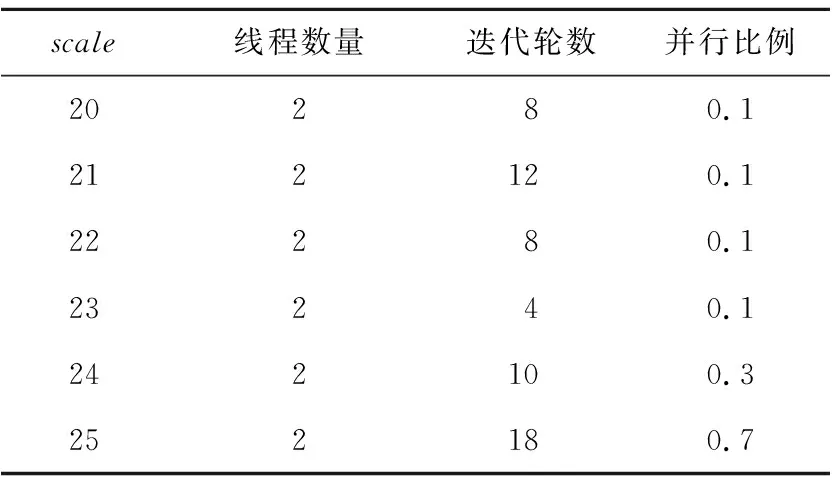
lbn (1) 随着规模n的增加,占用空间的平均增加速率如式(2)所示: (2) 由式(1)和式(2)可以得出空间开销平均增加速率的上限如式(3)所示: rate<2 (3) 这与遍历算法平均增加速率16相比更具优势。虽然在存储过程中没有存储边的信息,但达到了连通分量算法的基本需求。 并查集算法的合并和查找工作不需要一次性把连通分量中所有节点都找到,利用跳跃式、间断式的累加操作,来实现连通分量规模的逐步扩大,从局部连通分量扩展到全局连通分量,均可用分布式来实现,可以比较方便地并行化。但是,DFS需要不断往图的深处访问,不能适应在数据爆炸环境下的大图处理,在访问时需要把相连的节点一次性地访问完毕,难以实现分布式化。 此外,遍历算法还可以作为寻找生成树的基础和先导,在不增加算法复杂度的基础上,可以增加一些标志状态和判定状态的逻辑来判定有没有环的情况,这对后面的工作是十分有意义的。遍历算法和捷径向量算法的综合比较如表1所示。 Table 1 Comparison of traversal algorithmand shortcutting-vector algorithm 考虑到本文设计的串行算法的实现特点,由算法1可知,对查找操作有4种子情况: (1)2个节点均已被访问过,且根节点相同。此时不需要做任何操作,继续扫描下一条边。 (2)2个节点均已被访问过,且根节点不同。 (3)2个节点一个被访问过,另一个未被访问过。 (4)2个节点均未被访问过。 对于情况(2)~(4),下一步需要进行合并操作,把2个节点放置于同一个根节点之下。 对于情况(1),仅仅是判断根节点并跳过本条边,这与合并操作在算法逻辑上可以实现并行,即使情况(1)中出现了脏读,即读到了合并操作正在修改的脏数据,对边的状态的判断出现了差错,也不会影响结果的准确性。情况(1)与合并操作不需要作为2个事务来严格保证原子性,这为利用多线程并行加速提供了机会。 在本文设计的并行算法中,主线程(线程0)仍执行串行捷径向量算法,但需要其他线程对主线程要处理的边进行预分类,把不需要主线程处理的边筛掉,存储在连续存储的状态向量中。虽然主线程在处理边前仍然需要判断,但状态向量的存储空间是顺序存储,能进行线性连续地访问,减少了主线程的运行时间。 算法分成2个阶段: (1)串行阶段。 令主线程单独对数据集的一部分执行捷径向量算法,主要目的是更改若干节点的根信息,为下一步并行地预处理提供必要信息,只有一些节点已经位于相同的根节点下面时,才会出现需要优化访问的边。 (2)并行阶段。 对数据集的其余部分,多线程进行多轮迭代读取。主线程创建子线程,与子线程执行不同的操作。完成各自的任务后,执行栅栏同步,再开始新一轮的并行,直到多次轮转后把数据集处理完毕。 主线程和子线程分配相同大小的数据,子线程对属于自身的每条边进行判定,查看其2个节点是否有相同的根节点,设置相应的标志位,如果有,则说明不需要进行进一步处理,否则,需要主线程执行合并操作。 主线程主要分成2个阶段: ①处理本段数据。此时任务与子线程完全相同,只是不需要更改标志位,因为这已经是最终的处理结果,设置该步骤的目的是在等待子线程处理时不让主线程闲置。 ②处理剩余数据。当子线程处理完毕对应数据后,由主线程对每个子线程的数据分别进行处理,根据标志位来决定是否执行合并操作,直到把本轮所有数据处理完毕。 并行算法的流程如图 7所示。 Figure 7 Multi-thread shortcutting-vector algorithm图7 多线程捷径向量算法 实验环境的配置是:Intel(R) Core(TM) i7-7700K CPU @ 4.20 GHz;64 GB内存。操作系统为Ubuntu 16.04.7 LTS。 Graph500数据集采用的是Kronecker生成图,本文在不同规模的生成图下进行测试比较,其中,用参数scale来衡量图的大小,表示图中包含2scale个节点。 本文比较了并查集算法的数据结构与算法的不同组合的性能,如表 2所示,其中scale表示数据集的规模,即图包含2scale个节点。可以发现,若采用按秩合并,向量和链表2个数据结构的时间比较接近,但捷径向量比另外3种实现方式都要快,在220~225规模均取得了最好的性能,在scale=25(包含225个节点)时,与其他2个性能接近的算法的性能之比分别是1.38倍和1.40倍。因此,捷径向量算法具有显著的优越性。 Table 2 Performance comparison of Union-Find Algorithm 本文比较了3种算法对连通分量算法的时间开销,如图 8所示。可以看到BFS和DFS算法性能接近,捷径向量算法远好于遍历算法,在scale=25(包含225个节点)时,其对BFS、DFS的加速比分别为4.76倍和4.70倍,这符合本文的分析和预期。 Figure 8 Time comparison of connected component algorithms图8 连通分量算法时间开销比较 本文还测试了3种算法的空间开销,如图 9所示。3条折线对应主坐标轴,单位为int,表示占用整型变量的数量,2个长条柱对应次坐标轴,分别是捷径向量算法的空间开销占BFS、DFS算法存储开销的比例。可以看出,本文算法空间占用为另外2个算法的4.1%~4.6%,且增长趋势也较慢,有着明显的优势。 Figure 9 Storage comparison of connected component algorithms图9 连通分量算法空间开销比较 多线程程序中的可变参数包括:线程数量、并行处理数据比例和多线程并行迭代轮数,在不同的数据规模下,对参数取定若干有代表性的值,进行了多组实验。结果表明,并行算法与串行算法相比有着明显的性能提升,随着数据规模的扩大,并行的加速效果越来越明显,如图 10所示。在225节点规模的图中,加速比达到了1.57倍。 Figure 10 Performance comparison of parallel algorithm and serial algorithm图10 并行算法与串行算法的性能比较 在本文给定的数据规模下,使用2线程时,程序的性能最好。轮数大多数不大于10,对于并行比例,随着图规模的增大,取得最佳性能的并行比例越高,这也说明了并行的加速效果,如表 3所示。 Table 3 Parameter configuration for optimal performance of multi-threaded algorithm 本文针对面向大规模图遍历的连通分量算法,以Graph500生成的真实数据集为支撑,进行优化分析。连通分量算法和数据结构的优化,对Graph500测试的加速有着重要意义。连通分量算法找到的极大连通子图,为Graph500找到BFS最小生成树提供了辅助,合理利用了数据集节点的局部性,减少了无效的BFS根节点尝试,提升了节点划分的有效性,减小了节点间的通信开销。采用捷径向量算法对并查集算法进行了优化,并进行了算法和数据结构的协同度分析,对实现连通分量算法的3个基础算法进行了多维度比较和测试,并利用多线程迭代轮转进行了并行算法优化。实验结果表明,所提出的优化方法对其他方案均有着明显优势。向量作为一个常见的数据结构在面向图遍历的连通分量算法中表现较好,虽然它存在着一些不足,但通过与算法的配合,两者仍然能发挥出较好的效果。在后续的研究中,可以探索在本文研究成果的基础上,利用进程和线程混合并行来优化算法,这将极大提高本文算法的可扩展性。
3.3 多线程捷径向量算法
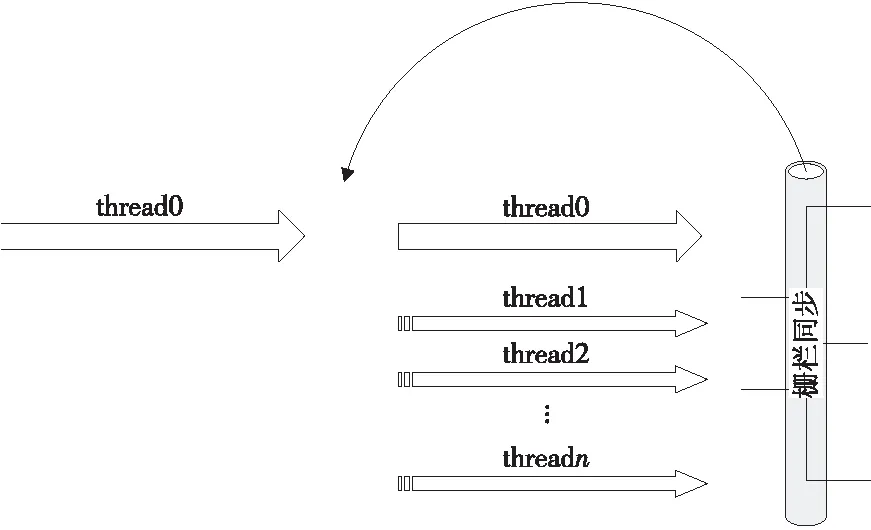
4 实验与结果分析
4.1 实验环境
4.2 捷径向量算法性能分析
4.3 连通分量算法3种实现时空开销分析
4.4 捷径向量算法的串并行比较
5 结束语
