钢箱拱桥扣锚索一体化施工控制简化算法研究
2022-03-22李智恒崔红梅曹和生
李智恒, 崔红梅, 曹和生
(1.重庆交通大学 土木工程学院, 重庆 400074; 2.重庆电讯职业学院, 重庆 402247)
拱桥斜拉扣挂施工法始于20世纪60年代,现已有上千座拱桥采用该施工方法建造[1],其难点在于主拱线形、扣索及锚索索力的计算与控制[2]。根据扣索和锚索布置形式,可将拱桥斜拉扣挂施工法分为扣索、锚索分离和扣锚索一体2类[3],其中对扣索、锚索分离体系已有广泛研究[4-9],而对扣锚索一体化研究的关注始于2000年。据不完全统计,目前国内已有20余座拱桥采用该施工方法建造,如表1所示。
文献[10]提到1996年顺利竣工的邕宁邕江大桥是我国首次采用扣锚索一体化施工的拱桥,但当时还未提到相应算法。相较于扣锚索分离,扣锚索一体在主拱线形和索力计算上将面临至少2个新问题:扣塔偏位和索-塔关系。文献[13]考虑到扣塔偏位的问题,故采用“定长扣索法”以避开其对计算结果的影响,该算法实质上是不考虑扣塔偏位的零摩擦法。为解决扣塔偏位和索-塔关系问题,韩玉[17]的博士论文研究成果指出,在“定长扣索法”的基础上考虑扣塔偏位的影响,可推导考虑扣塔抗推刚度的弹性支承刚度计算公式,用此方法计算主拱线形和施工索力。2种方法主要解决的是主动张拉索的索力计算问题,无论是在文献[13]中所采取将扣塔刚度视为无穷大的方法,还是在文献[16]中考虑扣塔抗推刚度的方法,均忽略了已有扣锚索对线形的影响。因此,需要进一步研究被动受力索对主拱线形和扣锚索索力的影响。
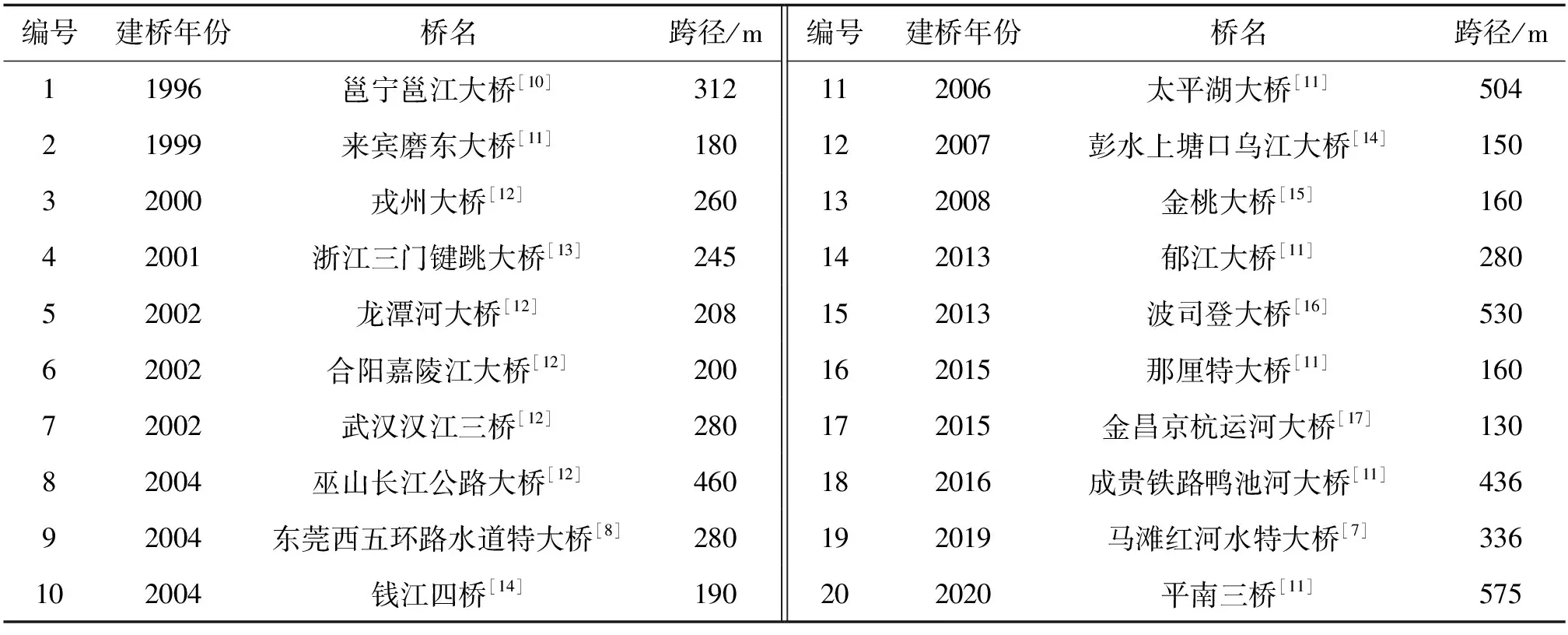
表1 采用扣锚索一体化施工的部分拱桥
在文献[13]和[16]的基础上,本文考虑扣锚索-扣塔-主拱的整体刚度,考虑到张拉索和非张拉索的工作方式和受力方式的差别,将索分为主动张拉索和被动受力索;针对扣锚索一体化中的扣塔偏位和索-塔关系,提出了“扣锚索一体化计算方法”,同时结合力矩平衡方程和变形协调条件推导相应方程;采用此算法计算拱桥扣锚索一体化施工时的线形和索力,并结合工程实测值验证算法的适用性。
1 问题描述
斜拉扣挂是拱桥常用施工法,其施工示意如图1所示,施工工序如图2所示,将拱段吊装至安装位置,利用扣索将其扣挂在扣塔上,调整索力使拱段处于悬臂平衡状态直至合龙。

图1 斜拉扣挂施工示意
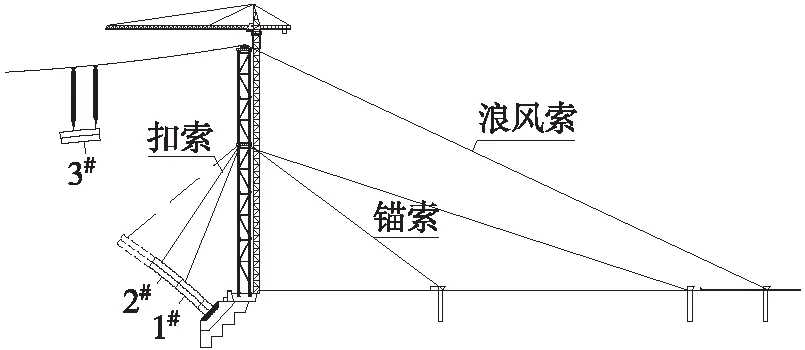
图2 斜拉扣挂施工工序
大部分拱桥采用斜拉扣挂施工时,扣索、锚索是分离状态,扣索和锚索分开张拉,通过控制扣索、锚索水平分力相等确保扣塔不发生偏位,该工法称为扣锚分离施工方法,在现有研究中其主拱线形和扣索索力计算已比较成熟。而少部分采用斜拉扣挂施工的拱桥,如图3所示,扣索、锚索是通长的同一根索,并通过安装在扣塔上的索鞍(U型钢板、定滑轮等)转至地面张拉,该工法称为扣锚一体施工方法。

图3 扣锚索一体化结构示意
索-塔间的静力关系如图4所示。图4中,将索鞍简化成安装在扣塔上的定滑轮,在不计摩擦力的条件下,索鞍两侧扣锚索索力相等。滑塔索关系和扣塔偏位问题就可以分解成3个子问题:1) 索鞍两侧的索力不相等时,索会沿索力小侧滑入索力大侧,引起两侧索长变化;2) 扣索、锚索水平夹角不完全相等,引起扣塔发生偏位,已张拉拱段的索力、索长和索夹角及主拱线形变化;3) 索与索鞍间存在摩擦力,实际工程中不存在完全光滑的情况,但在一定条件下仍可以忽略,研究时常作“零摩擦力”考虑。
2 基本假设与方程
拱桥采用扣锚索一体化施工过程中,根据索工作方式和受力机制不同可分为2种变化:主动变化和被动变化。安装节段i(1≤i≤N,N为拱节段数量)后紧接着张拉扣索i,此时扣索i称为主动索;除扣索i外,其他扣索称为被动索,被动索受力状态改变完全由外力控制,不能主动发生变化。扣索通过索鞍转至地面张拉锚固,不考虑索鞍处摩擦力和扣锚索垂度的影响,在此基础上建立以下计算体系。

图4 扣锚索一体化受力示意
2.1 主、被动索计算特点
1) 主动索张拉时会产生3类索力变化效应,分别为:(1) 增量效应:张拉扣索时,索力由0增加到Ti;(2) 旋转效应:由于本根扣索张拉,扣塔发生变形,引起扣索水平夹角、水平分力发生变化;(3) 弹性变形效应:由于扣索的张拉,本根扣索会发生弹性变形使索力发生变化。主动索计算时做出以下假设:索力改变,但扣索水平夹角不变,扣索不发生弹性变形,即仅考虑效应(1),不考虑效应(2)和(3)。
2) 被动索会产生2类索力变化效应,分别为:(1) 旋转效应:由于其他外力作用,扣塔发生变形,引起扣索水平夹角、扣索水平分力发生变化;(2) 弹性变形效应:由于外力的作用下,本根扣索发生弹性变形使索力发生变化。被动索计算时采用以下假设:扣索水平夹角不发生变化,只发生弹性变形,即仅考虑效应(2),不考虑效应(1)。
2.2 方程组建立与求解
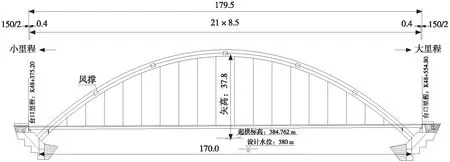
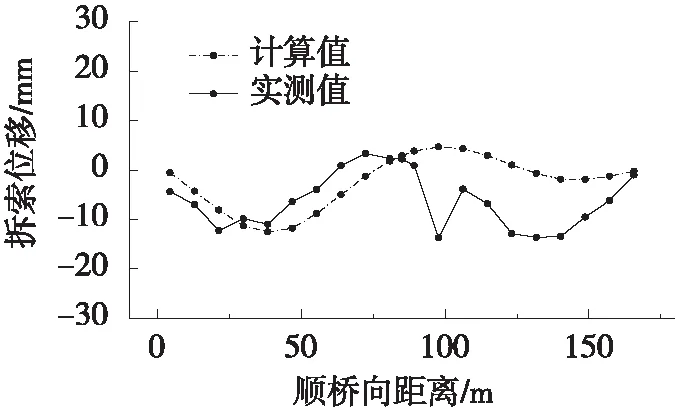
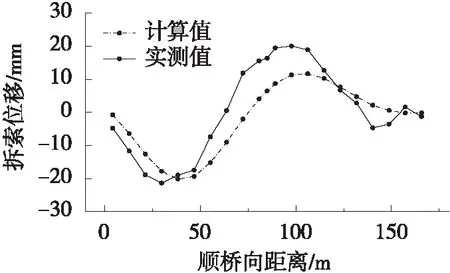
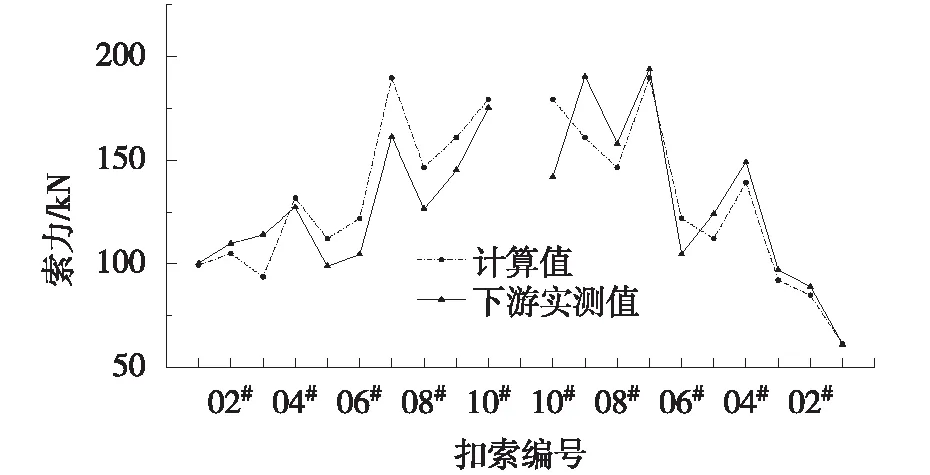
在主、被动索假设基础上,给出张拉1#、2#扣索时的实际施工图和相应的计算简图,推导、建立相应方程组并求解,其他工况类比1#和2#索的计算即可求得。公式中需要求解的未知量采用以下表述方式,ui:张拉i#索时扣塔的水平位移变化量;vZij:张拉j#索引起i#拱段下扣点的竖向位移变化总量;Tij:张拉j#索后i#索的索力值,当j=i时表示为i#主动索张拉时主动索的索力值;ΔTij:张拉j#索后i#索的索力变化量,ΔTij=Tij-Ti(j-1),如ΔT12=T12-T11,其中i 2.2.1 张拉1#扣索 实际施工过程中,张拉1#索如图5所示,为叙述和计算方便,将其简化为如图6所示的张拉1#扣索计算简图。此时1#索为主动索,虚线为张拉前的平衡状态,实线为张拉后的平衡状态,下同。O点为地锚点,F点为扣塔初始位置点,B点为1#拱段下扣点初始位置,张拉1#索后,F点移动到C点,B点移动到D点。记1#拱段与水平方向的夹角为θ1,1#索与水平方向的夹角分别为θ2、θ3。 图5 张拉1#索施工示意 图6 张拉1#索计算简图 根据扣塔的平衡条件和下扣点的位移协调条件,可得方程(1)、(2): T11(cosθ3-cosθ2)=K1u1 (1) T11δ11+vG11=vZ11 (2) 式中:Ki为扣塔刚度,根据索鞍位置取不同值;δij为j#索单位索力引起i#节段下扣点处的竖向位移;vGij为j#拱段自重引起i#节段下扣点处的竖向位移。 2.2.2 张拉2#扣索 实际工程中,张拉2#索如图7所示,并将其简化为如图8所示的张拉2#索计算简图。C点为1#索张拉后扣塔的位置点,D点为1#索张拉后主拱圈上1#扣点的位置点,G点为2#拱段下扣点初始位置。张拉2#索后,C点移动到J点,D点移动到I点,G点移动到H点。2#索与水平方向的夹角分别为θ2、θ4;1#索的原始索长(锚索加扣索总长)为L11,变化后索长为L12。需要求解的未知量有4个:u2,vZ12,vZ22,T12。 图7 张拉2#索施工示意 图8 张拉2#索计算简图 根据扣塔的平衡条件、下扣点的位移协调条件和胡克定律,可得方程(3)~(6): T22(cosθ2-cosθ4)+ΔT12(cosθ2-cosθ3)=K2u2 (3) ΔT12δ11+T22δ12+vG12=vZ12 (4) ΔT12δ21+T22δ22+vG22=vZ22 (5) (6) 式中:E为拉索的弹性模量;A为1#索的截面面积,ΔL=L12-L11。 2.2.3 方程组线性化 由于式(6)为非线性方程,需对式(6)进行线性化。设索鞍的坐标为C(xC,yC),其余坐标命名方式采用相同规则,根据图4和图5所示的几何关系,可得: (7) (8) (9) 2#索张拉过程中,索鞍处和扣点发生移动,索长随坐标连续变化,可以将索长L12看成坐标函数为:L12(xJ,xJ,xI,yI)。令xCO=xC-xO,yDC=yD-yC,其余命名方式相同,LCO可由坐标计算得到,则: (10) (11) 将式(11)泰勒展开保留高次项为: (12) 因此,将式(12)保留一次项化简可得: ΔL=u2·[xCO·(LCO-1-LCD-1)]+Δ12·(LCD-1·xCDtanθ1+yCD) (13) 2.2.4 方程组求解 在实际工程中,Ti是通过正装-倒拆法计算的初始索力[18-20],Ki可通过假设单位位移或有限元软件得到,δij、vGij可通过有限元软件得到,θi可根据几何关系和施工图纸求得。 当张拉1#索时,1#索为主动索,联立方程(1)、(2)便可求解X1和Δ11。张拉2#索时,1#索为被动索,2#索为主动索,联立方程(3)、(4)、(5)和(13)可得以下线性方程组: (14) 式(14)可求得张拉2#索时的4个未知量。计算后续张拉工况时,须借助前面工况的计算结果。随着拱段和扣索数量增加,未知数和方程数会逐渐增多,但未知数和方程的数量总是相等,可同样按照上述方法建立和求解方程组。 “扣锚索一体化计算方法”的流程如图9所示。主要步骤如下:1) 根据设计文件和资料输入正确的参数和边界条件,建立分施工阶段的成拱模型;2) 将索在索鞍处做固定处理,运用正装-倒拆分析法和零位移法,求解不考虑扣塔偏位和索滑移的初始索力;3) 提取各扣锚索一体化计算所需要的影响矩阵和参数;4) 根据相应的施工工况建立方程组,将第3步中求得的初始索力优化计算,借助计算机求解方程组,得到扣锚索一体化主拱的线形和索力。 某钢箱拱桥,其立面布置如图10所示。计算跨径为170 m,矢跨比1/4.5,拱轴系数m=1.37;拱轴线采用悬链线。全桥长179.5 m,宽10.0 m。拱肋采用等截面钢箱型截面,宽度为2.0 m,高度为3.0 m,板厚为20.0 mm。荷载等级为公路-Ⅰ级。 该桥主拱采用斜拉扣挂扣锚索一体化施工,小里程扣索通过索鞍转向至地面张拉锚固,大里程扣索则直接在山体上张拉锚固。主塔架采用Φ529×10 mm钢管作为主承重结构,每半幅塔采用4根钢管,标准节钢管长度为6 m,钢管间用Φ219×6 mm无缝钢管杆件作为平连杆。左右幅格构立柱间采用桁架结构横梁进行连接。索塔高62.8 m。 对该桥施工过程采用有限元软件Midas Civil建立模型,如图11所示。主拱圈及扣塔均采用Q345钢材。扣索采用高强度低松弛钢绞线,抗拉强度为1 860 MPa。主拱、主梁和扣塔采用梁单元模拟,扣索采用桁架单元模拟,拱脚、扣索和锚索锚固端均采用固结方式。拱箱和扣塔钢材的弹性模量取206 GPa,扣索弹性模量取195 GPa。 将成拱线形高程实测值与算法求出的计算值对比分析,其结果如表2和图12所示。 从表2和图12可以看出,成拱阶段下78%的高程偏差值能控制在30.0 mm内,表明按照本文算法计算的主拱线形进行施工控制,成拱线形与计算值吻合较好,其中成拱线形最大偏差为58.1 mm,最小偏差为1.4 mm,最大与最小偏差相差较大;且同一幅拱肋正负最大偏差的绝对值相加超过100 mm,究其原因可能是计算时未考虑环境温度对结构的影响,由于温差较大导致结构产生较大变形,此现象在钢结构拱桥尤为显著。 单位:m 图11 有限元模型 表2 成拱线形高程偏差 mm 图12 成拱线形高程偏差 上下游2幅拱肋合龙阶段至成拱阶段各控制点的位移如图13所示。由图13分析得到:成拱至合龙2幅拱肋线形总变化的实测值和计算理论值基本吻合,但是下游吻合更好。松索位移计算值和实测值最大偏差为17 mm,出现在大里程岸上游9#拱段,除此,其他拱段偏差均控制在10 mm内,进一步验证了该算法的可靠性。 (a) 上游 (b) 下游 对索力计算值和实测值作对比分析,结果如图14所示。从图14可以看出,两岸上下游扣索力实测值与计算值变化的趋势相同,施工索力最大相对误差为22%,最小相对误差为0.6%,大部分扣索的索力误差控制在10%内,表明该方法计算的结果与实际施工基本吻合,验证了该算法的可靠性。大里程扣索索力控制较小里程好,究其原因是小里程为扣锚一体化结构,而大里程为隧道锚结构,计算方法已经成熟,进一步间接说明扣锚索一体化施工工艺难以计算和控制,本文所述的计算方法还有待研究和提高。 (a) 上游 (b) 下游 本文对钢箱拱桥扣锚索一体化计算问题开展研究,将扣索和锚索根据其受力方式和结构特点,分为主动张拉索和被动受力索,同时考虑扣塔-扣锚索-拱段的整体刚度,提出“扣锚索一体化算法”。在主、被动索效应和零摩擦条件下,对一座实桥展开计算,结论如下: 1) 相较于以前扣锚索一体化的算法,将主、被动索分开考虑进行施工控制计算更加符合工程实际需求,主拱线形和扣索索力能得到有效控制。 2) 通过对比成拱线形的实测值和计算值,二值吻合良好。成拱线形大部分高程位移偏差控制在30 mm内;扣索索力误差大部分能控制在10%内。松索后两幅拱肋位移偏差绝对值最大为17 mm,90%以上控制点的位移偏差不超过10 mm,表明该算法可有效用于实际工程。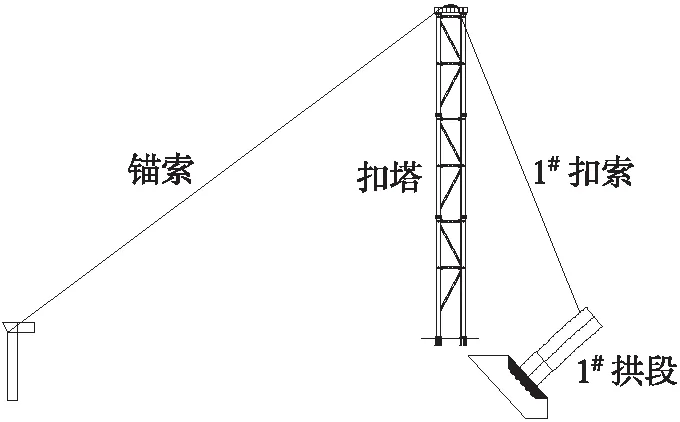



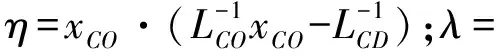
2.3 算法流程
3 工程算例
3.1 工程概况
3.2 有限元模型
3.3 计算值与实测值对比分析




4 结论
