一种基于NOMA的Q学习卫星通信随机接入方法

杨伟康，许小东

（中国科学技术大学中科院无线光电通信重点实验室 合肥 230026）

引言

面向机器类通信MTC（Machine Type Communications）的卫星通信网以其全天候、广覆盖、大容量及MTC 设备易部署等特点，受到业界广泛关注，已成为地面物联网IOT（Internet of Things）的有益延伸和补充。随机接入方法由于灵活性高、信令开销低和易实现的特点成为MTC 设备上行链路接入的有效解决方法。然而，海量MTC 设备试图在短时间内以随机接入方式接入卫星网络时，不仅会造成频繁的传输冲突，导致传输时延增加，甚至网络过载，而传输失败也会严重削弱MTC 设备的能量储备[1,2]。因此，在卫星通信网络中，研究具备有效过载控制机制的高能效随机接入方法，是改善卫星MTC 通信网络性能的可行途径之一。

近年来，学者们致力于将强化学习RL（Reinforcement learning）用作智能时隙选择策略，以弥补当前基于竞争的随机接入协议（如时隙Aloha）在性能上存在的严重不足。针对蜂窝网络，文献[3]就蜂窝网络中MTC 设备和人员如何共享随机接入信道（RACH）的问题提出了一种Q学习和时隙Aloha的组合方案。此方案通过Q学习智能地将时隙分配给MTC 设备，有效避免了多用户之间的碰撞冲突。与文献[3]中的二元奖励策略不同，SHARMA[1]等人根据演进型基站eNB（evolved nodeB）广播的RACH 拥塞程度标识设计奖励函数，提出了一种基于协作的分布式Q学习方案，不仅提高了系统的吞吐量，而且明显降低了MTC 设备的学习时间。进一步，MOON[2]等将Q学习和访问类别限制ACB（Access Class Barring）相结合，通过设定一系列可能的状态和动作，将碰撞概率和平均接入延迟用于定义奖励，使得eNB 可根据过载程度自适应调整ACB 控制参数，进而提高系统性能。文献[4]通过空间聚类和就近接入来克服MTC 网络拥塞问题，一方面缓解了接入拥塞程度，另一方面也降低了信号的传播损耗，节省了发送功率。此外，文献[4]还分析了学习率和奖励函数对收敛的影响，其结论对学习率和奖励函数的设置具有一定的指导作用。文献[5]针对卫星网络中多用户和多中继的卫星上行链路场景，提出了一种基于分布式Q学习的联合中继选择和访问控制方案。该方案中，设备的奖励由地面中继站计算和反馈而非来自卫星，在降低接入延迟上具有显著优势。

非正交多址访问NOMA（Non-Orthogonal Multiple Access）相较于传统的正交多址接入具有更高的频谱效率，被研究用于蜂窝和卫星网络的上行链路[6-8]。文献[9]将功率域的NOMA 技术和Q学习相结合，用于解决上行链路的子信道分配和功率控制问题，从而在短数据包通信中最大化MTC 网络的能量效率。SILVA[10]等人提出了一种基于NOMA的Q学习随机接入方案（NORA-QL）用于提高系统的吞吐量而非能量效率，同时考虑了路径损耗和衰落对性能的影响。在此方案中，时隙和发射功率和被组成（时隙，功率）对（下文用（t,p）表示），设备通过不断学习，找到唯一的（t,p）对进行传输。NOMA 技术使得由于选择相同时隙而发生碰撞的多个数据包仍可能被成功解调，因此系统吞吐量相较于文献[1]有了明显提高，同时需要的来自eNB的反馈比特更少。与上述方案不同，文献[11]针对具有突发流量的机器通信设备的特点，采用了随机分组到达模型。为了降低具有突发流量的MTC 设备对强化学习的影响，作者设计了基于设备活动概率的行动奖励，结合NOMA 技术，进一步提高了设备的成功访问概率。

本文针对卫星MTC 通信网络，在文献[10]的基础上对基于NOMA的Q学习随机接入方法（以下简称INORA-QL）进行改进，进一步提升系统在不同负载状态下的传输能效和吞吐率。文献[10]通过引入功率域NOMA 技术提高了系统的吞吐量，但同时也导致了更高的能量消耗，因为文献[10]中Q学习采用了贪婪算法，使得原本可以通过更加“智能”地学习、用低功率传输即可满足需求的设备不得不一直以更高的功率发送数据，导致能量效率低下。这对能量受限的MTC 设备是不可接受的，具体分析将在第2 节中详述。

为了解决能耗问题，首先依据发射功率和传输结果（成功/失败）设计奖励函数，同时根据卫星广播的全局信息改进Q学习的学习策略，并将学习速率设计为与迭代次数相关的函数形式，使得一帧中的每个时隙尽量只分配给单一用户，从而允许MTC 设备尽量以低功率发送数据，实现能效优化。其次，考虑到当系统过载时，即使采用文献[10]的NORA-QL 技术，仍会出现吞吐量迅速下降的问题。因此，本文进一步针对过载问题设计了一种基于学习过程中的Q 值特性和负载估计的ACB 新机制。通过上述两项改进，本文提出的I-NORA-QL 方法相比于文献[10]，能够在提高能量效率的同时，有效改善过载时系统的吞吐量。

1 系统模型

如图1 所示，本文考虑采用低轨（LEO）卫星通信系统，由于其具有相对更低的传播延迟和功率消耗，更适合面向物联网的机器类通信。在卫星覆盖范围内，K个MTC设备采用帧时隙Aloha协议尝试接入卫星网络。其中，一帧分为N个等长的时隙，每个时隙的长度都可满足数据包的传输要求。在一帧中，一个设备只能选择一个时隙发送数据，并且假定设备是积压的，即始终有要发送的数据包[1,10]。在每一帧的结尾，卫星发送一组反馈比特用于指示数据传输结果（成功/失败）。

此外，与现有工作相似，还假设：①所有的MTC 设备是全局同步的。② 卫星可对大尺度衰落和小尺度衰落的系数完美估计，因此本文不考虑衰落。③完美的串行干扰消除SIC（Successive Interference Cancellation）技术，即当一个数据包被解调后，通过信号重构可完全消除它对其他数据包的解调造成的干扰。

本文方案中的随机接入的整个过程可描述为：MTC 设备通过Q学习算法选择一个（t,p）进行一次数据传输，地面站依据当前解调情况得到ACB 参数和一帧中各时隙内数据包的碰撞情况，并将其通过卫星的下行链路广播给MTC 设备，其中前者用于过载控制，后者则是结合传输结果用于设备的Q 值更新，进而找到最优的传输策略，即最佳的（t,p）组合。

1.1 NOMA 中的SIC 技术

在TDMA 上行链路中，NOMA 技术允许多个设备通过使用不同的发射功率共享同一时频资源，接收机采用SIC 技术分离不同设备，实现资源复用。具体的，接收机使用SIC 技术先将较低功率的用户信号作为噪声，解调出信号功率较高的设备，然后从当前时隙消除较高功率信号的干扰，解调信号功率较低的设备信号。在接收端，第n个时隙的接收信号可表示为

其中，M表示一帧中选择第n个时隙的设备数（1≤M≤K），pm,n和xm,n分别表示第n个时隙中第m个设备的接收功率和传输信号，nw表示均值为0、方差为σ2的加性高斯白噪声。

本工作中，当一个接收信号的信干噪比SINR（Signal to Interference plus Noise Ratio）大于某个阈值γth时，则被认为解调成功。不失一般性，假设第n个时隙中M个信号的接收功率大小顺序为P1,n≤P2,n≤… ≤PM,n，则第m个设备的SINR为：

1.2 Q学习

Q学习是强化学习中的一种经典的无模型算法，具有计算复杂度较低、可在分布式场景下实现的优势[13]，适用于计算能力和能量受限的MTC 设备中。在该算法中，每个MTC 设备都相当于一个智能体来维护一张Q 表，通过不断行动来获取环境的反馈，并通过Bellman 方程来更新Q值。经过多次迭代，当算法收敛后，智能体就能根据Q值的大小找到最优的动作策略。Q值的更新算法为：

其中，s、α分别表示状态和动作，α为学习速率(0 ＜α＜1)，R为奖励，γ表示折扣因子，用来衡量未来奖励对Q值更新的影响。本方案中γ被设置为0，即不考虑未来奖励，这在考虑的场景中是合理的[1,5]。Q值更新算法为：

式中，（t,p）表示时隙和功率组合，Q(t,p)表示任一设备k，∀k∈{1,2,…,K}，对于（t,p）传输的偏好，每个设备根据前一次Q值和当前的奖励R对Q值进行更新。

1.3 ACB 机制

3GPP 提出采用ACB 来控制访问尝试以减轻LTE/LTE-A 网络的过载[12]。在该机制中，每个设备属于一个或更多的接入类别，某个设备如果属于接入允许类别，便可直接接入，否则如果属于接入受限类别，其接入将受到限制。具体的，受限设备在尝试接入时，首先产生一个介于0 和1 之间的随机数，如果该数不小于eNB 广播的ACB 限制因子，则该设备将在随后特定的限制期限内被禁止访问。

1.4 性能指标

在本文中，归一化吞吐量T，丢包率，平均功耗和低功率数据包占比作为指标用来评估本文所提方案的性能。归一化吞吐量定义为一帧中成功解调的数据包数与时隙数N之比，相应的，归一化负载G为设备数K与时隙数N之比。丢包率定义为一帧中未成功解调的数据包与总数据包之比。平均功耗定义为MTC 设备成功传输一个数据包的平均功耗。低功率数据包占比则定义为所有设备发送的数据包中，低功率数据包所占比例，与平均功耗共同用来评估能量效率。

2 改进方法

在这一部分，主要从能量效率和过载控制两方面改进了基于NOMA的Q学习随机接入方案[10]，降低了MTC 设备的平均功耗，同时提高了系统过载时的吞吐量。

2.1 基于Q学习的随机接入

文献[1]和文献[10]中的方案作为本文工作的基准，为了便于表述，分别被命名为Sharma-S 和Silva-S。其中，Sharma-S 中Q学习算法的操作流程为：

①在开始时，对于每个设备，Q 表被初始化为0。

② 每次传输，设备选择最大Q值对应的时隙，若最大值对应的时隙有多个，则从它们中随机选择一个。

③设备根据传输结果和eNB 广播的全局信息更新Q值。

④ 重复式（2）、式（3），直到收敛，即所有设备都找到唯一的传输时隙。

Silva-S 与Sharma-S 不同之处主要在于式（2），即每次传输中，设备选择最大Q值对应的（t,p）来传输数据。此外，Silva-S 只需要依据传输结果即可进行Q值更新。

2.2 能效优化机制

Silva-S 中功率域NOMA的引入，虽然提高了系统的吞吐量，但也导致设备功耗的大幅增加，能效降低。假设某个MTC 设备采用Silva-S 中的方法已经学到了最佳策略（即最大Q值对应的（t,p）），则其功耗增加的原因分析如下：

①若此时该设备使用高功率，而选择的时隙中只有其一台设备，那么实际上该设备可以采用更低的发射功率，因为此时接收端的SINR 只受白噪声的影响，但由于采用贪婪算法，因此设备将一直使用该策略，继续以高功率传输。

② 由于采用SIC 解调技术，对于存在两个及以上数据包的时隙，不仅解调复杂度增加，更重要的是为了能够成功解调，必然有设备需选择更高的传输功率来保证其SINR 大于某个解调阈值，因为此时功率较低的设备信号被当作噪声。而对于Sharma-S，当算法收敛后，每个时隙只分配给一个设备，此时影响解调的只有白噪声，从而只需要更低的发射功率。

因此，如何充分利用一帧中的所有时隙，使设备更加“智能”地以低功率在唯一的时隙中传输，成为解决上述问题的关键。

为了解决上述问题，在本文的能效优化机制中，首先，时隙和功率被组成（t,p），作为MTC 设备的动作集合。如前文所述，一帧被分为N个时隙，考虑PL，PH两种发射功率，因此每个MTC 设备共有N×2 个动作可供选择，即Q 表的大小为N×2，这与Silva-S 相似。然后，重点对Q学习的学习策略，奖励函数R和学习速率α进行了设计和改进。

2.2.1 学习策略

在能效优化机制中，接收端的解调器首先检测一帧中每个时隙内发生碰撞的数据包数CN n,n=1,2,…,N，这可以通过前导搜索器有效实现[14]，然后将此信息作为全局信息在一帧的结束时通过卫星的下行链路广播给所有设备，这与Sharma-S 类似。此时，MTC 设备便可以了解前一次传输时所选时隙和其他时隙的数据包的碰撞情况。与Sharma-S 区别在于，Sharma-S 利用eNB 广播的信息作为全局成本信息来设计奖励函数，本文则利用该全局信息改进Q学习算法的学习策略。

学习开始后，若设备k选择高功率PH在第n个时隙传输，如果传输成功，则：

①当第n个时隙的数据包数等于1 时，即只有设备k选择了该时隙，则在下一次传输时，设备k尝试选择低功率PL继续在第n个时隙传输。

② 当第n个时隙的数据包数大于等于2，即通过SIC 技术解调成功，则在下一次传输时，设备k首先根据接收到的全局信息，统计空闲时隙总数Nidle，然后以概率p(Nidle)使用低功率PL，在Nidle个空闲时隙中随机选择一个进行传输，p(Nidle)依据经验可采用如下形式：

式（5）表明空闲时隙越多，设备尝试低功率传输的概率就越大，使得一帧中的每个时隙尽可能只被一个设备占用，从而允许该设备使用低功率传输也可满足传输要求。

为了平衡Q学习的探索（Exploration）和利用（Exploitation），定义最大探索周期，即上述改进的学习策略在设备第一次尝试接入时启动，经过学习周期后结束，从而保证算法收敛后的稳定性。需要说明的是，该方案中的Q学习算法在整体上采用贪婪策略，设备k总是选择最高Q值的（t,p）作为它下一次的动作，则

其中，πk表示设备k下一次要采取的动作策略，即（t,p）的选择。

总之，本文提出的能效优化方法能充分发掘和利用卫星广播的全局信息，使MTC 设备在这些信息的协助下，更加“智能”地学习到最优策略，在保证传输成功率的前提下，降低传输功耗。

2.2.2 奖励函数

Sharma-S 中引入时隙的拥塞水平作为奖励函数，Silva-S 中则采用一个二元的奖励，即传输成功奖励R=1，传输失败奖励R=-1 。在本文中，发射功率被考虑用于奖励函数的设置。

其中，Pmax和Pmin分别表示允许使用的最高和最低发射功率，tP表示设备选择的发射功率，本文只考虑有限多的离散功率水平。

式（7）的设计以能量效率优化为出发点，其含义为，设备选择高功率传输时，如果传输成功，奖励相对较低，这将使设备偏向选择低功率以获得更大的奖励。如果传输失败，惩罚却更高，因为此时消耗了更多的能量，同时对其他数据包的解调也造成更大的干扰。此外，正负奖励的绝对值范围都为(0,ln2)，保证所有设备具有一致的行为[4]。

2.2.3 学习速率

不同于文献[1,3,5,10,11]中将学习速率α取为定值，我们根据文献[4]对α探究结论，从经验上将其设计为关于迭代次数的指数衰减函数。

其中，rinit为初始学习速率；rσ为衰减因子，控制α的衰减速度；β表示最小学习率[1,10]；t0为设备首次尝试接入的时间，t为迭代轮次，t-t0表示迭代次数。

式（8）表明在学习初期，α较大，即保留先前学习的经验较少，这有利于设备迅速将偏好转移到低发射功率上。随着迭代次数增加，α逐渐下降到最小学习率β，以使稳态对信道条件的微小变化（例如，偶尔的碰撞）表现出一定的鲁棒性[15]，算法1 总结了本文提出的能效优化机制。

2.3 过载控制机制

当海量MTC 设备同时接入卫星网络时，会造成系统过载，此时Silva-S的吞吐量会迅速下降，因此需要加入过载控制机制来改善其性能。由此，通过观察和研究设备在学习过程中的Q 值特性，结合负载估计，在优化能效的基础上，又加入了一种限制因子自适应的ACB 过载控制机制。

2.3.1 负载估计

针对随机接入中的负载估计或预测，目前已有很多工作对其进行了研究[16-18]。由于本工作主要关注Q学习算法的设计，因此，考虑采用通用的负载估计器[19]。假设ˆG为归一化负载估计值，G表示归一化负载实际值，则

ε∈[0,1]，表示负载估计误差范围，U为离散均匀分布。本文中，为ε设定某个固定值来表示系统的估计误差。

2.3.2 基本原理

首先依据归一化负载G定义系统的负载状态，定义如下

该机制中，当一个设备准备发送数据时首先初始化一个学习次数的阈值。设MTC 设备k经过次学习后的最大Q 值为在Q 表中出现的次数为。设备k经过次学习后，如果满足＜ 0且≥2的条件，则该设备在随后的接入过程将受到限制，即可认为该设备被分到接入受限类，否则该设备属于接入允许类。

在能效优化基础上，根据负载估计和Q 值特性，又加入一种新的ACB 方法用于过载控制。新ACB方法中限制因子pbar和设备的限制时间Tbar[12]分别为

其中，T、G分别为归一化吞吐量和负载，TACB为系统设定的限制时间常数，单位为帧。rand为区间[0,1]上均匀分布的随机数。由式（11）可知，当吞吐量T接近时，限制因子pbar接近0，从而防止更多接入受限类的设备的接入，保证系统持续处于高吞吐量状态。TACB和pbar由地面站确定，并同上文提到的一帧中各时隙发生碰撞的数据包数一起由卫星广播传输给MTC 设备。算法2 描述了过载控制机制。

3 仿真结果

在该部分，首先验证了所提方案I-NORA-QL在能效优化和过载控制上的有效性，然后探究了控制α衰减速率的衰减因子rσ对能效的影响，参数设置如表1 所示。注意，由于发射功率PL、PH值的设置，一个时隙中最多允许两个设备同时接入，否则无法解调成功，因此吞吐量的上限Tupper=2.0，对应上文=2。

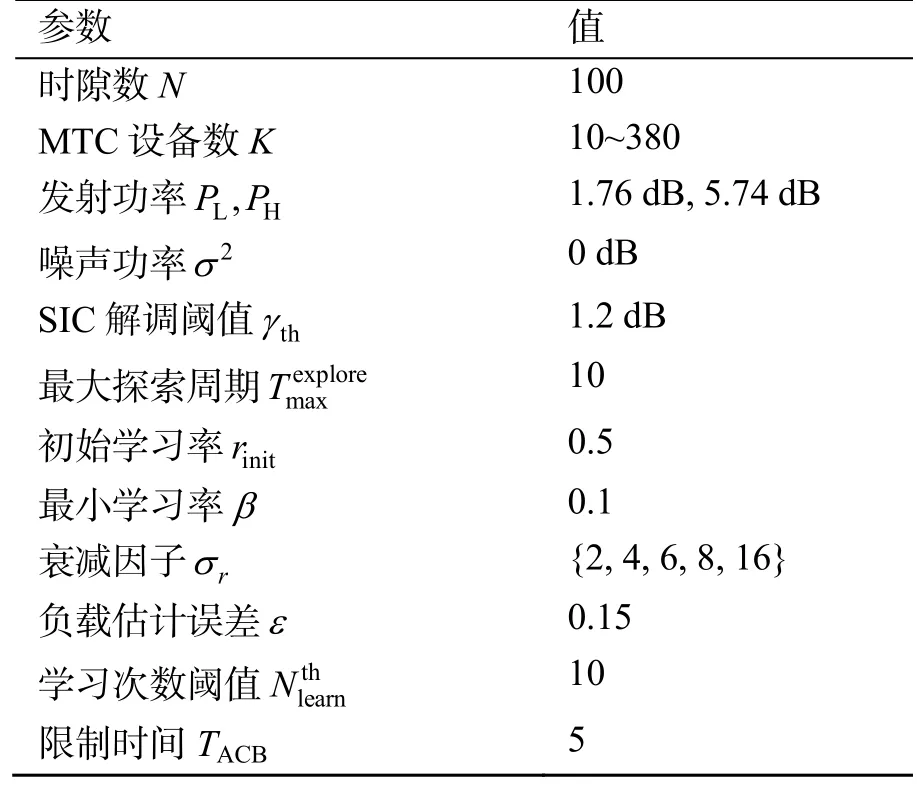
表1 仿真参数设置Table 1 Simulation parameter settings

3.1 能效性能

为了对比的公平性，Silva-S 中也加入本文提出的过载控制机制，命名为Silva-S-OC。每个设备成功传输100 个数据包的平均功耗和低功率数据包占比的比较如图2 所示。

从图2（a）中可以看出，当K≤80(G≤0.8)时，在I-NORA-QL 中，设备平均功耗接近设置的低功率PL=1.5（1.76 dB），对应到图2（b），此时几乎所有设备都选择低功率传输，这是由于设备数K小于时隙数N且相差较大，使设备在探索过程中，更容易找到唯一的时隙并以低功率PL传输数据。当80＜K≤200 时，随着K的增加，系统的负载逐渐加大，为了保证能成功传输，设备必须以更高的概率使用高功率进行传输，使得平均功耗逐渐增加，最终与Silva-S-OC 几乎持平。在图2（b）中，则表现为低功率数据包的比例逐渐下降。而对于Silva-S-OC，在非过载时（K≤200），无论何种负载，其平均功耗一直稳定在2.6 左右，即高、低功率数据包几乎总是各占总数的一半，这导致平均功耗相较I-NORA-QL大幅度增加。当K＞250 时，虽然此时I-NORA-QL 低功率数据包占比略高于Silva-S-OC，但平均功耗相较Silva-S-OC 却有增加，且当K＞300 时，平均功耗增加的幅度会随着设备数的增加而迅速增大，这是由于当系统过载严重时，I-NORA-QL 中设备对低功率的偏爱反而不利于整个系统的收敛，使得接入成功率下降，碰撞增加。因此，所提方案适合工作在归一化负载G＜3.0的情况，并且可在G＜2.0 时较为显著地降低设备的平均功耗。

因此，I-NORA-QL 在系统非过载状态下能够降低MTC 设备的功耗，负载较低时尤为显著，从而增加电池的使用寿命。特别地，当归一化负载G≤0.8 时，本方案等价于Sharma-S 中设备只使用低功率PL传输。由此，I-NORA-QL 综合了Sharma-S 和Silva-S 在不同负载下的优势，在提高系统吞吐量的前提下，通过改进Q学习算法优化MTC 设备的能量效率，确保设备的长期工作。

3.2 衰减因子 rσ 对能效的影响

设置σr=2,4,6,8,16，得到5 种不同衰减速率的学习速率α，同时将固定的α=0.1作为参考，观察和分析σr与平均功耗的关系。

如图3 所示，首先证明了将学习速率设置为指数衰减形式在提高能效上的积极作用。当设备数K＜200 时，随着rσ的增加，不同负载下设备的平均功耗相对就越低，但降低的程度在减小，这是因为rσ为α(t) 标准差，rσ越大，α(t) 衰减越慢，因此设备在学习阶段的初期，它的学习速率相对就更大。由式（4）可知，学习速率越大，设备保留之前学习的经验就越少，因此将更关注当前的奖励，使其更快地从当前选择的策略跳转到另一个更佳的策略，即使用低功率传输，实现能效优化。此外，由3.1 节分析可知，随着设备数的增加，设备将以更高的概率使用高功率以保证传输成功，因此设备的平均功耗快速增加，从而也导致不同σr参数下平均功耗的差异逐渐减小。而当K≥200，σr取过大时（对应σr=16），其平均功耗相较于其他σr值有所增加，并且增加量随着负载的增大而增大，由2.2.3 节分析可知，一个更大的σr值将导致学习速率在更长的时间内保持较大的值，这在学习阶段的后期，会使设备对信道条件变化的鲁棒性降低，不利于系统的收敛，造成更多的碰撞和能量消耗，并且这种情况会随着负载的增大而加重。因此综合考虑，rσ取值区间为[6,8]，此时可更好地平衡不同负载下设备的平均功耗。

3.3 过载控制性能

为说明I-NORA-QL 在过载时的性能优势，我们比较了Silva-S、I-NORA-QL-FixedBar 和I-NORA-QL在吞吐量和丢包率上的表现，如图4 所示。I-NORA-QL-FixedBar 中的ACB 限制因子设定值pbar=0.5[20]。

当K≤160 时，系统负载还未过高，三种方案中的所有设备几乎都能通过Q学习找到唯一的（t,p）对进行传输，因此，图4（b）中的丢包率极低，接近0。当160＜K≤200 时，系统逐渐接近过载，此时I-NORA-QL 和I-NORA-QL-FixedBar 吞吐量上略低于Silva-S，这是由于这两个方案的过载控制机制被激活，使得经过学习后仍无法找到最佳策略的少量设备被禁止继续传输，而Silva-S 中设备由于没有限制，可以进行更多次的失败和重传，直到找到最佳的学习策略，因此吞吐量有些许提高。当K＞200时，系统过载并且逐渐加重，Silva-S 吞吐量迅速下降，丢包率迅速上升，而对于加入ACB 过载控制的I-NORA-QL 和I-NORA-QL-FixedBar，经过一定的学习周期后，未找到最佳（t,p）对的设备自动地被分到接入受限类，从而减少了参与竞争的设备数，大幅降低了丢包率，同时避免了更多能量的白白消耗。随着过载程度的加重，由于I-NORA-QL-FixedBar 中的限制因子pbar为定值，缺少自适应能力，因此它的吞吐量逐渐低于I-NORA-QL，而丢包率逐渐高于I-NORA-QL。

通过以上三个方案的比较，一方面验证了将依据负载估计和Q 值特性的ACB 方法加入到基于NOMA的Q学习随机接入的有效性，另一方面也表明了自适应的ACB 限制因子能够更有效地提高系统的吞吐量，降低丢包率。

为详细展示加入过载控制机制后的数据传输过程，设置K=240，每个设备需要成功发送100 个数据包，在一次实现过程中，传输数据的设备总数和成功传输的设备数的变化曲线如图5 所示。

4 结束语

本文主要研究了Silva-S 存在的传输能效低和系统过载时吞吐量下降的问题，并对其进行改进。功率域NOMA的应用虽然提高了系统的吞吐量，但也导致设备功耗的增加，降低了能量效率。为了解决这个问题，从Q学习本身入手，利用所需的全局信息，对Q学习的学习策略进行改进，同时将发射功率作为参数用于奖励函数的设置，学习速率不再固定为常量，而是被设计成随迭代轮次递减的函数形式。实验结果表明，I-NORA-QL 能够降低设备的平均功耗，在负载较低时更加显著，这对能量受限的MTC设备至关重要。此外，本文还探究了影响学习速率的衰减因子rσ对平均功耗的影响，我们发现当rσ取值在[6,8]之间时可在能效上产生更加积极的作用，并结合Q学习的特点分析了原因。I-NORA-QL 中的过载控制则是利用设备学习过程中的Q 值特性和学习效率之间的关系，为设备设定学习次数的阈值，当设备学习次数超过该阈值，并且其Q 值满足设定的条件时，该设备将被划分至接入受限类，其随后的接入过程将受ACB 限制因子的控制，并且限制因子与系统的负载和吞吐量相关。I-NORA-QL 中的过载控制机制保证系统在过载时，依然能维持高吞吐量和低丢包率。