基于回归分析的航天器异常检测方法
2022-03-22史晓云郭小红符叶丹王新广
史晓云,陈 军,郭小红,符叶丹,王新广
(1 航天器在轨故障诊断与维修重点实验室 西安 710043 2 宇航动力学国家重点实验室 西安 710043)
引言
航天器遥测数据能够实时动态反映航天器的运行规律,但是其数据关系非常复杂且专业性强[1],故总体上呈现海量、多源、异构、时空多序列等特点,隐含着大量有价值的信息没有得到充分的挖掘和应用。因此,如何精准、快速定位航天器故障,预测航天器状态和改进航天器服务,已成为目前航天领域遥测分析中亟待解决的问题。
在轨航天器遥测数据一般按照缓慢变化、周期变化和突变进行分类,总的来说,它的变化呈现出趋势性、季节性、周期性以及随机性[2]。在轨管理的实际过程中,主要通过阈值法对航天器进行异常检测,其优点是检测过程简单,但是存在虚警、漏警现象,时效性也差。现阶段,在针对大量遥测数据的研究中,主要基于时间序列模型,将实际遥测值与模型输出值比对,实现对遥测数据的异常检测。文献[3]对航天器遥测数据的变化趋势进行分类,研究了多种主流的数据预测理论并分析了其适应性,总结提出一种基于历史遥测数据的在轨卫星故障预警系统构架;文献[4]利用M-VMD 方法对遥测数据进行分解,提取各模态分量的熵特征,通过计算遥测数据与样本数据对应的各模态分量的JRD 距离,实现在轨航天器异常状态识别。随着信息技术的发展,基于专家知识和物理模型的故障诊断方法已经难以满足高实时性和高准确性的故障处置需求,尤其是随着大数据时代的来临,航天器系统的各种特征属性、运行机理以及一些无法解释的复杂机理,都可以通过实时数据间的某种关联关系进行分析研究。
本文通过回归分析方法对某航天器电源温控系统相关实测数据进行尝试性研究,通过特征提取和数据预处理,对正常状态下的时序参数值进行建模,并与异常时段的时序参数值进行对比。实验结果表明,该算法以多元数据为背景可以有效检测遥测数据趋势,可及时发现遥测时序数据潜藏的异常变化,从中挖掘出各部件及器件缓慢变化的的异变信息[1],能有效提升在轨航天器的管理能力,从而确保航天器在轨安全可靠运行。
1 回归分析方法
航天器参数之间互相关联、互相耦合,它的数值和系统运行模式变化受多种遥测参数的共同影响。在实际问题中,常常会遇到相互联系、相互制约的变量,包括确定性和非确定性两种关系,回归分析就是研究有一定的关系但又不能用确定的函数进行表达的统计方法,它既可以探索和检验自变量和因变量的因果关系,也能用自变量的取值变化来预测因变量的取值,是一种定量处理多个变量相关关系的方法[1]。在现实工作中,回归分析的优点在于它可以通过统计手段对干扰因素进行控制,发现自变量和因变量的关系,从而及时掌握航天器的当前状态。
1.1 特征选取及预处理
为了简化分析,一般只保留权重影响因子较大的特征遥测参数。一方面可以简化预测过程,另外对今后设计改进有着重要的参考价值。由于遥测数据受多种因素影响,采用3δ 标准差原则进行野值剔除。
1.2 回归模型
航天器遥测参数种类繁多,找出参数间隐含的相关关系有利于在轨卫星管理人员根据航天器实时状态实施安全有效的管控[5]。一般用皮尔逊系数对线性相关进行判别,用互信息法对非线性相关进行判别,对于强相关性的参数通过构建映射函数或模型进行预测[6]。回归模型是一种统计分析方法,因变量根据自变量进行“预测”,从而使“预测值”以最大可能性接近因变量的“观测值”[5]。很显然,由于随机误差等因素,回归方程中的预测值不可能和预测值完全相同,回归分析的特点在于它把观测值分为结构和随机两部分[5],结构部分是因变量与自变量间的结构关系;随机部分是未被结构项解释的剩余部分。
一元线性回归模型:只有一个特征是输入变量,被称作单变量线性回归问题[5]。回归模型表示如下:
多元线性回归模型:在航天器的实际工作中,遥测因变量的变化随着重要因素的变化而变化,此时就需要用两个或是更多的影响因素作为自变量来解释因变量的变化,多元回归就是研究多个随机变量与一个可控变量间的相关关系,n代表特征参数的数量,xn代表第n个特征的遥测参数的取值,支持多变量的预测函数可表示为[7]:
式中,Y是因变量,代表随机观测值,未知参数β0,β1,…βi,…,βn为偏回归系数,βi(i=1,2,······,n)则是在其他自变量固定不变的情况下,xi(i=1,2,······,n)每改变一个单位,其单独引起因变量Y变化的平均改变量,ξ为去除k个自变量对Y影响后的随机误差[5]。
在多元线性回归方程中,模型必须满足以下条件:
①自变量对因变量有显著的影响,并表示出非确定关系(线性关系);
② 样本的容量>回归系数个数;
③残差服从正态分布。
多元线性回归模型建成之后,必须进行评价和检验,才能判定模型是否可以应用。模型的检验能够通过考察模型的绝对平均差、线性相关等指标及模型预测误差图,来综合评价模型的可应用性并比较模型的效果。
1.3 评价回归方程的参数
由上述方法确定了模型的相关参数后,需对其进行一定的评价,来确定模型的预测情况,一般常用的评价指标有:协方差矩阵、离差平方和、残差平方和、回归平方和、拟合优度检验[5]。
①有多个变量时,可建立归一化的协方差矩阵,用以表示多变量间的相关关系,并用于航天器参数异常检测[5]。协方差:假设有随机变量X、Y,其协方差为:
② 协方差矩阵:设n维随机变量(x1,x2,······,xn)的二阶混合中心矩[5]:
i,j=1,2,······,n都存在,则称矩阵:
为n维随机变量(x1,x2,······,xn)的协方差矩阵,显然有cij=cji。
③总偏差平方和表征的是每个因变量的实际值与因变量平均值的差的平方和,即反映了因变量取值的总体波动情况,即被回归方程解释的因变量的总变异[8]:
④ 回归平方和表征的是因变量的预测值对其平均值的差的平方和,它是由于自变量x的变化引起的y的变化,反映了y的总偏差中由于x与y之间的线性变化引起的y的变化部分,可以由回归直线解释[8]:
⑤ 残差平方和又称误差平方和,表征的是因变量的各实际观测值对其回归值的差的平方和,它是除了x对y的线性影响之外的其他因素对y变化的作用,不能由回归直线来解释[8]:
⑥ 拟合优度反映回归方程所解释的变异在因变量总变异中所占的比例,判断回归方程的拟合程度,表示拟合直线能多大程度反映因变量的波动[8],变化范围为0~1,决定系数越大,说明方程的预测准确性越高,原因变量对结果变量的解释程度越高,越接近1 说明拟合效果越好。
拟合完方程的参数后,就要对回归模型进行检验,在简单线性回归中用测定系数来验证方程的拟合程度,而在多元线性回归中,如果在模型中增加一个自变量,模型R2往往会相应地增加[9]。
2 仿真实验及结果分析
为验证本文提出的回归分析方法的正确性和可行性,选取某型号在轨运行航天器驱动机构滑环典型故障时的电源温控系统相关遥测参数进行实验验证,分别对正常状态下的时序曲线、异常发生后的时序曲线进行建模分析。
某在轨航天器运行过程中蓄电池充电电流减少了2/3,卫星进入最小能源安全模式,有效载荷全部自主关机,航天器姿态稳定,其他分系统工作正常。本文针对某在轨航天器电源温控系统典型故障案例,绘出了在轨故障过程中的主要遥测参数曲线。
如图1 所示,当航天器出现异常时,与异常相关的遥测参数值时序图形态发生畸变,目标遥测参数在异常出现前后有明显变化。由于本文所选遥测参数值均为连续变量,回归分析更简单有效,故本文利用回归分析方法,通过遥测参数间的相关性对航天器趋势进行预测,有助于及时发现航天器异常情况并给予相应的控制。
2.1 特征选取
为了减少遥测数据的特征数量,本文使用皮尔逊相关系数对某航天器在轨运行过程中电源温控系统相关40 个遥测参数进行选取。经过实验仿真,选择了与航天器驱动机构温度高度相关的特征参数:蓄电池A、B 组的充电电流、充电阵A、B 阵电流、太阳电池板温度及驱动机构温度遥测参数作为特征变量,变量均为连续型。通过对正常状态和异常状态时的相关系数进行对比发现,当航天器出现部件异常时,遥测参数间的相关关系已经发生变化。
如表1 所示,可以看到正常状态时7 个自变量与因变量的驱动机构温度相关系数均超过0.8,当航天器各分系统正常运行时,相应的遥测参数具有确定的关系,它们之间的关系为高度正相关;异常状态时,如表2 所示,相关系数出现了明显变化。因此,本实验可以通过回归分析对驱动机构温度变化进行预测。

表1 正常状态Pearson 相关性Table 1 Normal-state Pearson correlations
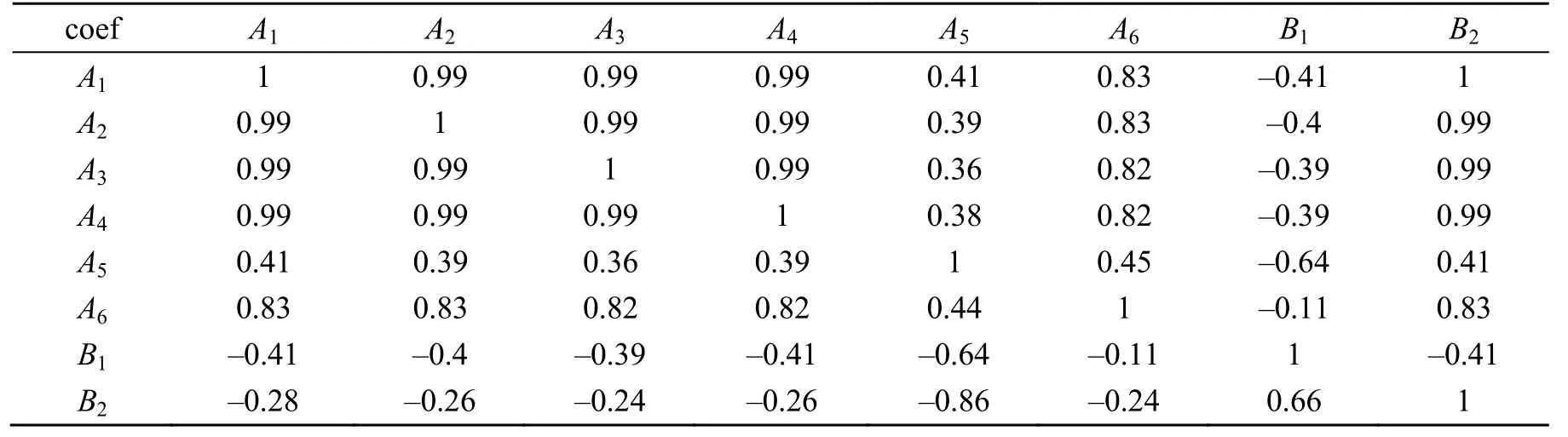
表2 异常状态Pearson 相关性Table 2 Abnormal-state Pearson correlations
2.2 数据预处理
航天器遥测数据受多种因素干扰,会出现数据不连续,野值或者明显不合理的值,这些情况对建模有一定的干扰,因此需要对遥测数据进行预处理,本文通过用3 倍标准差剔除不合理的点;根据时间顺序,依次对正常状态时的500 个样本点和异常发生后264 个样本点进行实验。
数据预处理:根据参数范围,首先根据3δ 标准差原则剔除数据中因解码等原因造成的野值,并将上述8 个重要参数分别按30 s 一条进行挑点存储。
本实验以驱动机构温度为因变量,基于回归的预测方法以其余电源温度相关遥测参数为自变量进行回归分析,建立驱动机构因变量相对应的回归方程,进而求解预测值。
2.3 回归建模
根据最小二乘法做线性回归拟和,如表3 所示,可得回归方程为

表3 回归系数Table 3 The regression coefficients
由式(10)、式(11)可以得出,该典型异常发生前回归模型与正常状态下的回归模型不匹配,影响因素的权重发生了明显变化,从而可以说明航天器遥测参数趋势已经发生改变。
2.4 显著性检验
根据表4 实验结果所示,由OLS 最小二乘法可以得到,正常状态时模型的拟合优度为99.3%,说明该回归模型拟合精度高,对应的是0.007,说明回归显著,回归结果可靠;异常状态时模型的拟合优度为0.779,说明该回归模型拟合精度较好,对应的是0,说明回归显著,回归结果可靠。

表4 OLS 回归结果Table 4 OLS regression results
3 结束语
本文根据某航天器典型异常案例,对遥测数据进行了回归分析的异常检测,主要做了数据预处理,回归系数、数据拟合建模及显著性检验,通过对不同时段的航天器遥测数据的回归方程进行检验,从而得出航天器的状况是否前后一致。它主要解决以下问题:①从数据角度出发,确认遥测参数间是否具有相关性,如果有,确定它们之间究竟满足何种数学关系,即经验公式或是回归方程,并对它的可信度做统计检验;② 从对同一个遥测参变量有影响的多个特征变量中,选取具有显著系数的参数;③利用航天器遥测数据去推算回归函数,尤其是对随机变量Y的观测值做出点预测和区间预测。
本文提出的方法可用于故障检测,通过遥测数据的不断积累,对回归方程不断进行更新迭代,不断提高检测的准确性,从而可推广应用于其他航天器。
