基于前景理论的城际公共客运客流敏感性分析
2022-03-22崔洪军张凤云朱敏清
崔洪军,张凤云,朱敏清,姚 胜
1)河北工业大学土木与交通学院,天津 300400;2)河北工业大学建筑与艺术设计学院,天津 300400
随着城市群的不断发展,群内各城市间的紧密联系产生大量客流.在综合交通竞争日益激烈的环境下,城际高铁实现公交化运营模式,使城际高铁成为城际客流运输的主要交通方式.城际高铁客流呈现明显分布不均匀性,一些线路在早、晚高峰时段客流量过多、过度拥挤,影响旅客舒适度;而在较大正供需差额时段客流量较少、上座率低,大量浪费铁路运输资源.长期静态统一的票价体系使票价丧失了调节供需匹配关系的杠杆作用.因此,城际公共客运在不同时段的客流敏感性研究对缓解城际公共客运的供需矛盾具有重要意义.
在客流敏感性分析中,一些学者将出行者认定为完全理性人,PENG等[1]建立基于均衡价格敏感性分析模型,获得均衡交通下各类交通的客流量以及不同交通方式的客流敏感性.余玲[2]提出改进巢式logit(nest logit,NL)模型,用于划分城际交通方式,进一步构建客流敏感性分析模型.王婕[3]根据出行距离不同建立不同NL模型,分析城际铁路分担率在不同出行距离下对各个影响因素的灵敏度,指出不同出行距离场景下提高城际铁路分担率的最优方案.也有研究将出行者认定为有限理性人[4-7],郭鸿钧等[8]研究一种前景理论(prospect theory,PT)与灰色关联方法相结合的运输通道出行方式选择方法,运用多项logit(multinominal logit,MNL)模型计算运输通道内出行方式的分担率.马书红等[9]将出行方式和出行时段结合,建立基于NL-累计前景理论的出行方式选择预测优化模型.XU等[10]建立基于前景理论的出行决策模型,分析客流对出行时间成本、出行费用成本和出行舒适成本的敏感性.
上述研究均以全时段进行客流敏感性分析,而不同出行时段的出行者时间价值不同,面对票价调整的敏感性呈现不同特征.因此,本研究将高铁出行时段划分为负供需差额时段、较小正供需差额时段和较大正供需差额时段,各时段划分以中国铁路网站(www.12306.cn)中车次发车前30 min二等座余票状态为依据.3个时段区分为:①某一时间段内所有车次余票状态均为“候补”或“无”时,则此时段为负供需差额时段;②某一时间段内所有车次余票状态均为“有”时,则此时段为较大正供需差额时段;③其他情形则为较小正供需差额时段.考虑不同时段并认为出行者是有限理性人,建立广义出行前景成本最小配流模型分析不同时段票价变动对不同交通方式的客流敏感性.
1 交通特性分析
在城际公共客运客流敏感性分析中,仅针对常见的城际高铁、普通铁路和长途客运方式,其交通特性如下:
1)经济性指标C1(单位:元)通过购票网站获得的票价表示.
2)快速性指标C2(单位:元)通过城际出行方式所花费的货币时间价值表示,为

其中,出行方式花费时间t1(单位:h)可以通过购票网站获得.出行者的时间价值Vt(单位:元/h)用平均收入水平及创造收入价值的时长表示,利用单位工资率描述具体出行者的时间价值[11],为

其中,rk为k时段的出行者月平均收入;u为1个月的劳动天数,按平均值22 d计;T为一日的劳动时间,按平均8 h计.
3)便捷性C3(单位:元)为出行者到达车站、离开车站到达目的地、进出站和在车站等待时间消耗的货币时间价值,为

其中,t2为便捷性时间(单位:h).
4)舒适性C4(单位:元)为交通工具的舒适性,不易定量分析.研究表明,交通工具的舒适度与票价有关,C4约占经济性指标C1的16%[11].
5)准时性C5是旅客较为看重的出行方式特性之一,车辆早到或晚到都会影响旅客的出行计划.准时性C5用准点率表示.
6)安全性C6是旅客出行的重要考虑因素.不同出行方式的安全性用伤亡事故率与极限事故率衡量[11].
7)低碳性C7(单位:kg/人)通过人均CO2排放量表示[12].低碳出行是政府倡导的一种出行方式,随着全民环保意识的加强,出行者也将越来越关注出行方式的碳排放量.
2 基于前景理论的最优配流模型构建
2.1 前景值计算
1)决策矩阵
构建原始决策矩阵X k为

其中,Xkij为k时段出行方式i对应的第j个交通特性值;k=1,2,…,g;i=1,2,…,n;j=1,2,…,m.由于原始决策矩阵中交通方式各特性值的单位量纲不同,需对原始决策矩阵进行无量纲化处理,为

变换后决策矩阵R k为
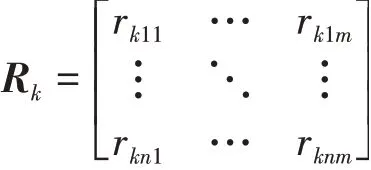
2)参照点选择
用t表示出行者类别,设t=1为城际高铁出行者;t=2为普通铁路出行者;t=3为长途客运出行者.当t=1时,参考点S1为城际高铁对应的7个交通特性值,即经济性、快速性、便捷性、舒适性、准时性、安全性及低碳性指标值,计算为S1={xk11,xk12,xk13,xk14,xk15,xk16,xk17};同 理,当t=2和t=3时,参考点S2和S3分别为普通铁路和长途客运对应的7个交通特性值,即S2={xk21,xk22,xk23,xk24,xk25,xk26,xk27},S3={xk31,xk32,xk33,xk34,xk35,xk36,xk37}.
3)确定前景值函数
第t类出行者的前景价值函数为
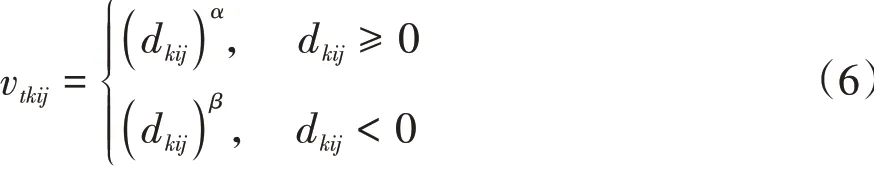
其中,vtkij为第t类出行者在k时段的价值函数;dkij为相对损益值,即为各指标值与参考点的差值;α和β为风险敏感系数,取α=β=0.88[13];λ为损失规避系数,取λ=2.25[13].
4)前景值计算
设第t类出行者在进行交通方式比选中面对收益的权重函数为面对损失的权重函数为即

其中,wtj为交通特性对应的权重,通过层次分析法确定;γ为风险收益态度系数,一般取γ=0.61[14];δ为风险损失态度系数,一般取δ=0.69[14].
第t类出行者在k时段对交通方式i的前景值为
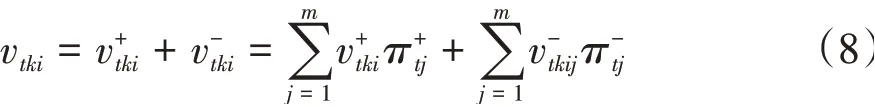
k时段交通方式i的综合前景值vki为

2.2 最优配流模型构建
2.2.1 广义出行前景成本函数构建
广义费用函数f一般是与客流量有关的增函数,f采用幂函数表示[15],用交通方式i在k时段的前景值vki代替效用值,构建广义出行前景成本函数,具体形式为

其中,qki为k时段内第i种交通方式的交通量(单位:人次);vki为k时段交通方式i的综合前景值;a和b为待定参数,一般取a=1.14、b=0.35[11].
2.2.2 最优配流模型构建
做如下假设:①常态下城际通道内交通方式日客流需求量不大于供给量;②城际通道内仅有城际高铁的票价变化,其他交通方式的票价不变;③高铁日客流量存在负供需差额、较小正供需差额和较大正供需差额时段.
在上述假设条件下建立广义出行前景成本Z最小配流模型为

其中,Q为城际通道日客流量(单位:人次);k为高铁出行时段,k=1为负供需差额时段,k=2为较小正供需差额时段,k=3为正向供需差时段.
2.3 客流敏感性分析
出行者流量对票价变动的敏感程度通过客流敏感度表示,即

其中,πki为k时段交通方式i的客流敏感度(单位:人次/元);Δqki为客流量的转移量(单位:人次);ΔC为高铁票价的变化量(单位:元).
票价变动下出行者流量变动速度通过客流敏感度变化率表示为

其中,yki为k时段交通方式i的客流敏感度变化率;Δqki为客流量的转移量(单位:人次);qoki为原高铁票价下k时段交通方式i的客流量(单位:人次).
3 实例分析
本研究以中国天津—北京客运通道公共客运客流为研究对象,分析城际公共客运客流敏感性随高铁票价的变化情况,研究仅考虑客流在公共交通方式之间的转移.采用调查问卷方式,于2020-10-26至2020-10-30在问卷星上发放调查问卷,共得到问卷522份,其中,有效问卷475份.问卷涉及出行者的个人属性和出行属性等内容.整理分析后得到各时段出行者的平均收入,根据式(1)计算得到,负供需差额时段、较小正供需差额时段及较大正供需差额时段的时间价值分别为35.2、30.8及29.4元/小时,因此,可得天津—北京运输通道内的3种交通方式的各时段交通特性指标值,如表1.

表1 各时段交通方式指标值Table 1 Traffic modeindexesof each period of time
3.1 前景值计算
1)构建决策矩阵
根据式(2)—(3)得到负供需差额时段3种交通方式的决策矩阵R1为

第1类出行者的参考点为S1={0.460,1.000,0.920,1.000,1.000,1.000,0.270};第2类出行者的参考点为S2={1.000,0.330,0.910,0.430,0.990,0.960,1.000};第3类出行者的参考 点 为S3={0.470,0.280,1.000,0.920,0.710,0.910,0.330}.
3)前景值计算
根据式(5)可得,第1类出行者的权重为π+={0.13,0.31,0.17,0.22,0.29,0.22,0.13}、π-={0.11,0.32,0.16,0.21,0.29,0.21,0.11};第2类出行者的权重为π+={0.31,0.18,0.22,0.17,0.18,0.30,0.14}、π-={0.31,0.16,0.21,0.15,0.16,0.30,0.12};第3类出行 者 的 权 重 为π+={0.26,0.12,0.35,0.15,0.15,0.30,0.08}、π-={0.25,0.10,0.37,0.13,0.13,0.30,0.06}.
根据式(7),取P1=P2=P3=1/3,可得负供需差额时段交通方式i的综合前景值为v11=-0.081、v12=0.212及v13=0.423.
重复以上步骤也可得到,在较小正供需差额与较大正供需差额时段交通方式i的综合前景值.天津—北京城际客运通道内较小正供需差额和较大正供需差额时段交通方式i的综合前景值分别为v21=-0.144、v22=-0.301及v23=-0.475;v31=-0.180、v32=-0.387及v33=-0.402.
3.2 交通量计算
将以上综合前景值带入系统最优配流模型式(8)中,取Q=30 164人次[16],利用交互式线性和通用优化求解器Lingo进行求解,得到不同时段各出行方式的客流量qki,如表2.

表2 不同时段各出行方式的客流量Table2 Passenger flow of different travel modesin different time 人次
3.3 客流敏感性分析
高铁票价变动下的客流量变化趋势如图1.其中,图1(a)、(b)及(c)分别代表负供需差额、较小正供需差额及较大正供需差额时段的票价.可见,当不同时段票价降低(提高)时,客流量变化最大的均为高速铁路,其次为普通铁路,最小为长途客运.随着不同时段票价的降低,对应时段高铁客流量的吸引量大幅增大,随着不同时段票价的提高对应时段高铁客流量的流失量均逐渐趋于稳定,表明天津—北京的出行者对票价提高的敏感性比票价降低时要小,且当票价不断提高时,出行者对票价的敏感性将逐渐降低,最终趋于一个较小值.

图1 天津—北京客流量变化趋势Fig.1 Tianjin-Beijing passenger flow trend
图2为负供需差额时段票价变动下的客流敏感度.可见,在负供需差额时段,票价降低比票价提高对客流敏感性的影响更大.当票价降低10%~50%时,不同时段3种交通方式的客流敏感度都在增大,其中,π11以大幅度增大;π12、π21及π31以较小幅度增大;π22、π13、π32、π33及π23一直保持较小水平,最小的π23为5.0~7.6人次/元,表明票价降低对长途客运、较小正供需差额时段普铁和较大正供需差额时段普铁出行者的影响较小.

图2 负供需差额时段票价变动下的客流敏感度Fig.2 Passenger flow sensitivity under ticket price change during period of time with negative supply-demand difference
当票价提高10%~50%时,不同时段3种交通方式的客流敏感度均逐渐减小,π11以较大幅度减小;当票价提高20%后,π32、π33及π23在低于5.8人次/元基础上发生微小变化;当票价提高30%后,π22和π13在低于8.3人次/元基础上发生微小变化;当票价提高50%后,π21、π12及π31发生较小变化.
图3为较小正供需差额时段票价变动下的客流敏感度.可见,在高铁较小正供需差额时段,票价降低比票价提高对客流敏感性的影响大.当票价降低10%~50%时,不同时段3种交通方式的客流敏感度均增大,其中,π21以大幅度增大;π11、π31、π12及π22以较小幅度增大;π32、π23、π33及π13一直保持较小水平,最小的π13为5.3~8.4人次/元,表明票价降低对长途客运和较大正供需差额时段普通铁路出行者的影响较小.

图3 较小正供需差额时段票价变动下客流敏感度Fig.3 Passenger flow sensitivity under ticket price changeduring period of timewith small positive supply-demand difference
当票价提高10%~50%时,各个时段3种出行方式的客流敏感度均减小,其中,π21以较大幅度减小;当票价提高20%后,π23、π32、π33及π13在低于4.7人次/元基础上发生微小变化;在票价提高40%后,π31、π22及π12在低于9.9人次/元基础上发生微小变化;在票价提高50%后,π11和π12在低于14.1人次/元基础上发生微小变化.
图4为较大正供需差额时段票价变动下的客流敏感性.可见,在高铁较大正供需差额时段,票价降低比票价提高对客流敏感性的影响大.当票价降低10%~50%时,不同时段3种交通方式的客流敏感度均增大,其中,π31增大幅度大;π11、π21及π12以较小幅度增大;π22、π33、π32、π13及π23一直保持较小水平,最小的π32为3.5~5.7人次/元,表明票价降低对长途客运、较小正供需差额时段和较大正供需差额时段高速铁路出行者的影响较小.

图4 较大正供需差额时段票价变动下客流敏感性Fig.4 Passenger flow sensitivity under the change of ticket priceduring period of timewith large positive supply-demand difference
当票价提高10%~50%时,不同时段3种交通方式的客流敏感度均减小,其中,π31以较大幅度减小;当票价提高20%后,π22、π32、π33、π12及π23在低于9.3人次/元基础上仅发生微小变化;当票价提高50%后,π11和π12在低于12.4人次/元基础上发生较小变化.
综合图2至图4可见,当票价降低10%~50%时,对应最大客流敏感度变化值排序为Δπ31(63.8)<Δπ21(65.1)<Δπ11(69.8);当票价提高10%~50%时,对应最大客流敏感度变化值排序为Δπ11(33)>Δπ21(27.7)>Δπ31(22.6).对于出行者来说,负供需差额、较小正供需差额及较大正供需差额时段票价降低均比票价提高的敏感性大.虽然负供需差额时段高铁票价提高时客流敏感性最大,但与票价降低时的126.4和196.2相比,票价降低对应客流敏感度约为票价提高对应客流敏感度的2倍.
图5(a)、(b)及(c)分别代表负供需差额、较小正供需差额及较大正供需差额时段的票价.可见,随着票价降低,不同时段3种交通方式的客流敏感度变化率接近线性增长,表明随着票价降低,交通方式的客流敏感度将以更大速度增大.负供需差额、较小正供需差额及较大正供需差额时段票价降低对应的最大客流敏感度变化率排序为y11<y21<y31,表明降低较大正供需差额时段票价比降低负供需差额和较小正供需差额时段票价对相应时段高铁客流量增长速度的影响大.负供需差额、较小正供需差额及较大正供需差额时段票价提高对应的最大客流敏感度变化率均小于22%,表明票价提高对各时段各交通方式的影响较小.票价降低对应客流敏感度变化率约为票价提高时的2倍.
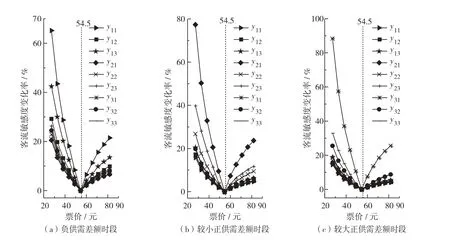
图5 客流敏感度变化率Fig.5 Passenger flow sensitivity changerate
结 语
本研究将高铁出行时段划分为负供需差额时段、较小正供需差额时段及较大正供需差额时段,在交通特性指标中添加低碳性指标,基于前景理论构建7个交通特性指标下的决策矩阵,以各类出行者所选择交通方式的交通特性值指标为参考点,建立前景价值矩阵,进而计算不同时段各交通方式的综合前景值.以广义出行成本最小为依据,构建广义出行前景成本下的最小配流模型,计算城际客运通道内不同出行方式各时段的客流量,进一步构建客流敏感性模型和客流敏感度变化率模型,分析天津—北京城际客运通道公共客运客流敏感性和客流敏感度变化率.结果表明,①不同时段高铁票价变动时,各时段各交通方式的客流敏感性变化趋势大体相近.票价降低50%至票价提高50%时,各时段各交通方式的客流敏感性呈下降趋势,并逐渐趋于稳定;②不同时段高铁票价降低时,各时段各交通方式客流敏感度变化率接近线性增长,且降低较大正供需差额时段票价时的客流敏感度变化率大于降低负供需差额和较小正供需差额时段;③不同时段高铁票价提高时,各时段各交通方式的客流敏感度保持平稳,但其客流敏感度达到平稳状态时,对应的票价提高百分比不同.
以上结论表明,在不同时段适当调整高铁票价可有效优化交通运输结构,较大正供需差额时段运输资源浪费和负供需差额时段运能不足、旅客舒适度差的现象也可以得到改善.后续研究可通过对节假日客流特征的解析,探讨工作日和节假日票价变动时的客流敏感性差异.
