基于缓冲时间的共享车位分配鲁棒方法

薛召杰，袁秋芳，季楷丰

1）深圳大学土木与交通工程学院，广东深圳 518061；2）深圳大学滨海城市韧性基础设施教育部重点实验室，广东深圳 518061；3）深圳大学未来地下城市研究院，广东深圳 518061；4）深圳市前海智慧交通运营科技有限公司，广东深圳 518052

随着共享经济的快速发展，人们逐渐接受并认可资源共享理念．通过车位共享平台，可以充分利用车位的空闲时段，有效提升有限车位资源的利用效率，为缓解城市停车难问题提供新思路．共享停车平台的车位分配很大程度上决定着平台收益和供需客户服务质量等，研究平台车位分配问题具有重要的经济价值和现实意义．

针对共享停车平台车位分配问题，LU［1］建立适合老社区的停车资源共享模型，以期缓解停车压力．KASPI等［2］比较了部分停车预订策略、停车位详细预订策略以及完整停车保留和非预订策略，并给出每个策略的详细用户行为模型，通过离散事件仿真评估不同设置下的系统性能．SHAO等［3］在离散时间窗刻画的停车供需基础上，建立了使平台收益最大化的二元整数线性规划模型．YANG等［4］针对多个停车场的车位分配问题，分析车位分配的主要影响因素，建立以总效益最大化为目标的数学模型．孙会君等［5］以平台运营商收益最大化为目标，建立共享车位的租用与分配模型．张水潮等［6］提出一种以平台收益与停车步行距离为优化目标的共享车位分配模型．

在预约停车的实际应用中，需考虑停车不准时问题，即停车用户相对于预约时间提前到达或延迟离开的不确定性．JIANG等［7］考虑停车不准时性的共享车位分配问题，建立消费者和车主在不同时段的停车概率函数和混合整数规划模型来确定最优解．RAN等［8］考虑停车者偏好、共享停车场景可行性、停车需求动态分布及局部因素随机性等因素，提出一种辅助决策的双层模型．HUANG等［9］分析车辆到达数量和停车时间的随机分布，建立以停车效益最大化为目标的共享停车分配模型，并根据停车效益最大化原则，确定预留停车位的最佳比例及向居民购买共享停车位的数量等．相较于预留停车位，本研究提出一种较为简单的缓冲时间预留方法，以车位共享平台收益和分配鲁棒性作为目标，研究平台车位的分配问题．

1 车位分配问题建模

本研究基于短时提前预约模式，即平台在收集完所有停车需求、车位供给时间及数量等信息基础上，再进行车位资源的最优分配．

1.1 平台收益最大化模型

基于连续时间窗描述建立平台收益最大化的车位分配模型．令S为供给停车位的总数，记停车位k的供给时间窗为[ak，bk]；令D为停车需求总数，记需求i的预约停车时间窗为[ci，di]；令ps和pb分别表示平台对车位的售价（对停车用户的单位时长停车收费价格）和进价（从闲置车位出租方租入停车位的单位价格）．有限的车位资源一般不能满足所有停车需求，μ为拒绝1个需求的惩罚成本．

定义0-1决策变量xik表示停车供需分配结果，若需求i被分配在停车位k，则xik=1，否则，xik=0；定义0-1决策变量yk表示平台是否租入车位，yk=1为平台租入车位k，否则，yk=0；定义0-1决策变量zij表示同一车位上不同停车需求之间的时序关系，zij=1表示需求i在j之前，否则，zij=0．

基于整数规划模型的平台收益最大化共享停车平台车位分配问题模型为

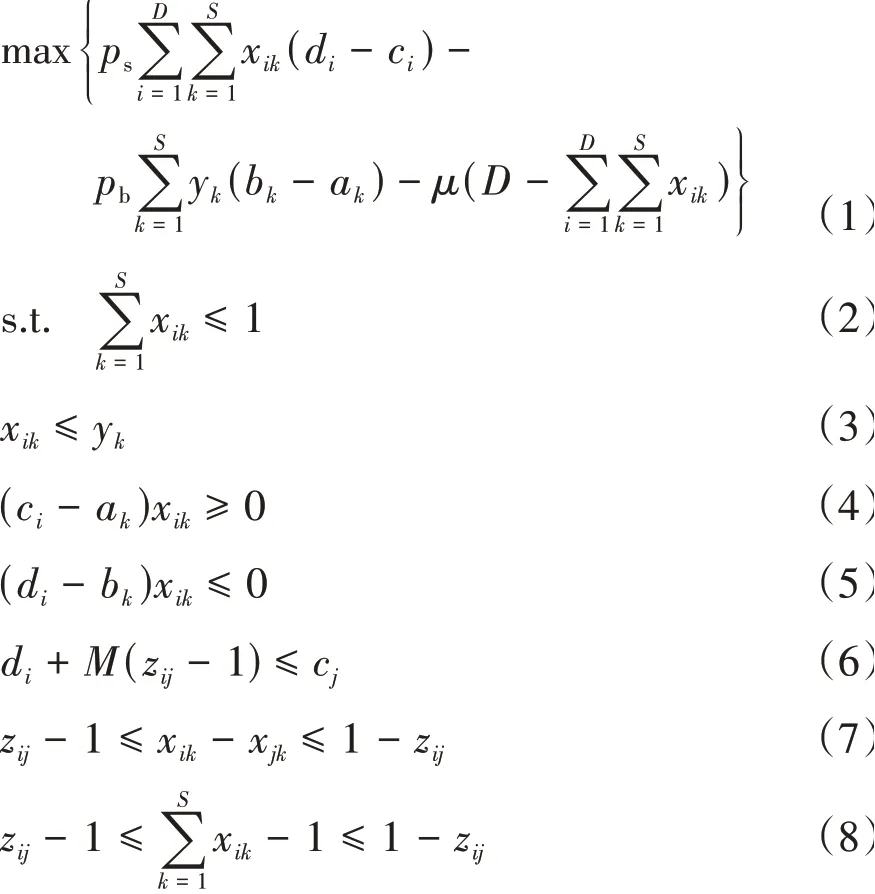
目标函数（1）表示最大化平台总收益，其中，第1项表示向停车用户收费的总收入；第2项表示租入停车位花费的总费用；第3项表示因拒绝部分需求造成的惩罚损失．约束（2）表示1个停车需求至多分配给1个停车位．约束（3）表示只有当车位被平台租入时，需求才能被分配到该车位上．约束（4）和（5）表示若需求i分配到停车位k，则应满足需求i的停车时间窗在停车位k的供给时间窗内，否则，若ci＜ak或di＞bk，则xik=0．约束（6）限制了分配在同一车位上前后两个停车需求之间的时间窗关系，其中，M为极大值．约束（7）至（9）表示当zij=1时，需求i和j必须接受且分配给同一个停车位，即若zij=1，则xik=xjk且约束（10）表示当需求i和j分配到同一停车位时，i在j的前面或后面，即若xik=xjk=1，则zij=1或zji=1．约束（11）定义0-1决策变量．

1.2 鲁棒性最大化模型

当停车需求相对预约时间提前到达或延迟离开时，会将平台根据预约时间生成的车位分配方案打乱，甚至导致方案不可行．因此，本研究通过预留缓冲时间应对一定的时间不确定性，原理如图1．假设需求i、j及j'均预约车位k，且j和j'的停车时长相同，可行的分配结果如图1．其中，图1（a）的分配方案仅考虑平台收益最大化，当需求i延迟离开或j提前到达时，可能会因为需求j无法正常停车导致损失；图1（b）方案预留一定的缓冲时间，这样当需求i短时间延迟离开或j'提前到达时，方案依然可行．因此，图1（b）方案较图1（a）方案更优．

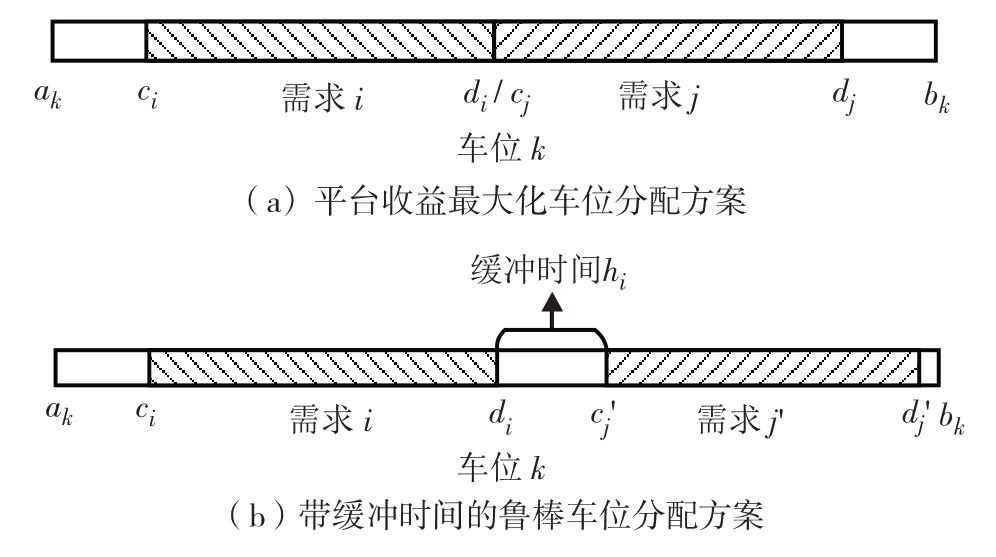
图1 缓冲时间原理示意Fig.1 Schematic diagram of buffer time

以下讨论如何通过缓冲时间刻画鲁棒性大小．记hi为车位分配方案中需求i之后的缓冲时间长度，考虑到边际递减效应［10］，需求i的鲁棒性g(hi)为

不同车辆在准时方面具有不同声誉，令需求i的不确定性系数为wi，则需求i的鲁棒性变为wig(hi)，则鲁棒性最大化目标函数为

约束条件为

其中，约束（15）限定若需求i未被接受，则hi=0；约束（16）限定需求时间窗与缓冲时间和车位供给时间窗之间的关系；约束（17）限定同一车位上前后需求时间窗和缓冲时间之间的关系．

1.3 双目标优化模型

引入目标权重系数λ(0≤λ≤1)表示平台对收益最大化和鲁棒性最大化目标函数的偏好，则双目标数学规划模型可转换为如下的单目标数学模型，

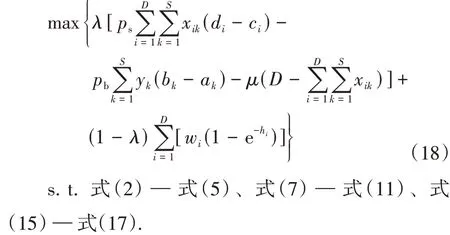
2 数值实验

本节通过求解不同规模的随机算例验证模型有效性．假设车位供给时间处于常规工作时间段09∶00—18∶00，具体的供给时间窗和需求时间窗通过Matlab生成，供给时间窗为均匀分布，需求到达符合泊松分布，停车时长满足负指数分布．参数ps=10、pb=5、μ=1，wi为1～10的随机整数．

2.1 目标函数线性化

由于目标函数中包含的非线性项1-e-hi难以求解，采用分段线性函数近似拟合非线性曲线．根据单位时间长度分段，则g(hi)的近似拟合表达式为

分段线性拟合曲线如图2．实线表示原函数g(hi)=1-e-hi，虚线表示分段拟合线性函数．可见，hi=4后曲线基本可以完全重合．

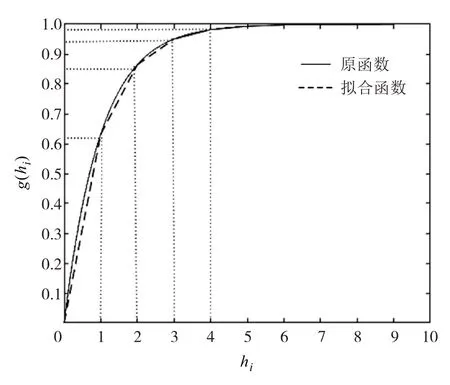
图2 非线性函数g(hi)=1-e-hi的线性拟合曲线Fig.2 Linear fitting plot of nonlinear function g(hi)=1-e-hi

为了将分段线性函数转化为线性约束，将g(hi)以分点f0=0、f1=1、f2=2、f3=3、f4=4及f5=9的5段线性函数(m=5)，并引入变量uil，则hi和g(hi)可表示为

s.t.式（2）—式（5）、式（7）—式（11）、式（15）—式（17）及式（20）—式（26）.

2.2 不同规模算例求解

基于上述线性规划模型，在配置为AMD 3.60 GHz CPU和16 GByte RAM电脑上采用商业求解软件CPLEX对15组随机生成的算例进行求解．车位供给数从1递增至15（步长为1），停车需求数为对应供给数的5倍，λ=0.8．求解得到的总目标函数值、平台收益、鲁棒性、最优分配方案的接受供给数、接受需求数、车位利用率指标及计算时间见表1．其中，算例1-5表示供给车位数为1，停车需求数为5车位；利用率表示接受的需求总时长与接受的供给总时长之比；计算时间＜0.5 h．

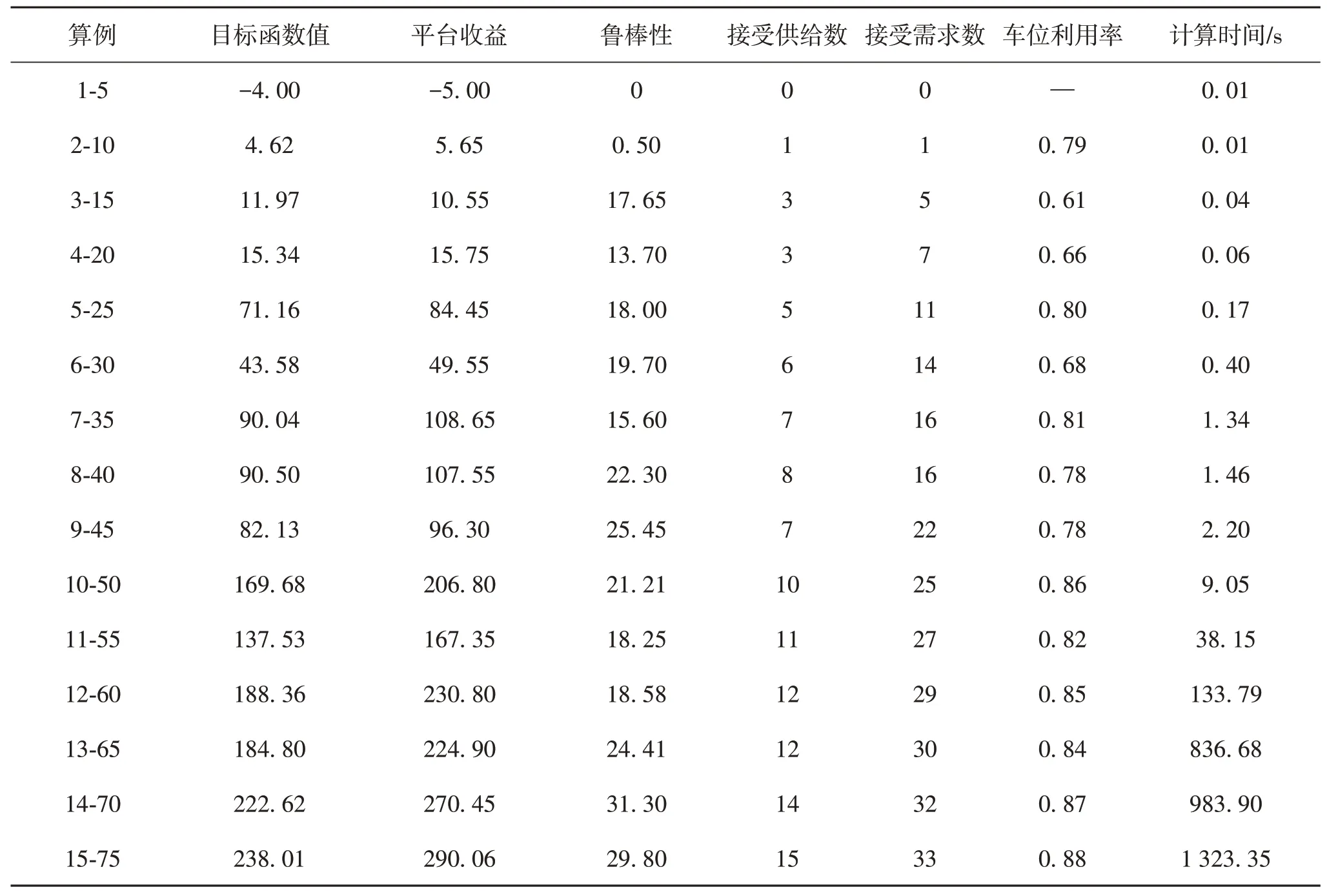
表1 不同规模算例求解结果Table1 Solutionsof different scaleexamples

2.3 灵敏度分析

选择算例5-25进行灵敏度分析．保持其他参数不变，只改变λ（λ从0.01到0.99，步长为0.01），得到不同λ值下的平台收益与鲁棒性，及平台收益-鲁棒性的近似Pareto前沿分别如图3和图4．5个典型的车位分配方案见图5．

图3 不同λ值下的平台收益与鲁棒性Fig.3 Platform revenue and robustness with differentλ

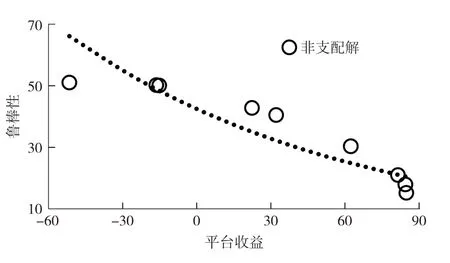
图4 平台收益-鲁棒性的近似Pareto前沿Fig.4 Approximate Pareto front of platform revenue-robustness

图5 不同λ值下的匹配方案Fig.5 Allocation schemeswith differentλ

由图3可见，随着λ的增大，平台收益分段增加，而鲁棒性分段下降．当λ=0.01时表示最注重鲁棒性，当λ=0.99时表示最注重平台收益．在λ值变化范围内，平台收益从-51.55升到84.85，鲁棒性从51.07降到15.28．

图4中的9个非支配解是当λ从0.01变化到0.99这99个最优解里筛选出的．非支配解拟合出的虚线表示近似Pareto前沿，靠近左上角的解偏向鲁棒性，靠近右下角的解偏向平台收益．从左上角到右下角，单位平台收益增加引起的鲁棒性减少量逐渐增加，减少量的变化范围从0.02到6.75．

图5中的空白矩形分别代表5个停车位S1—S5的供给时间窗，实心矩形代表接受的停车需求，用D1—D25表示．可见，随着λ值的增大，矩形之间的间隙减小．当λ=0.01时，接受9个停车需求，拒绝16个；当λ=0.20时，接受13个停车需求，拒绝12个；当λ=0.40时，接受12个停车需求，拒绝13个；当λ=0.60和0.80时，接受相同的11个停车需求，拒绝了14个；当λ=0.99时，接受10个停车需求，拒绝15个．随着λ值的增大，虽然平台收益增加，但是应对不确定性的能力（鲁棒性）降低．根据不同λ值，平台给出不同的匹配方案以达到平衡总收益和鲁棒性的目的．

结 语

在共享车位分配中，通过预留缓冲时间的方法解决时间不确定性因素，建立平台收益最大化与鲁棒性最大化的双目标优化模型．①通过双目标优化模型，在合理时间内可以求解出算例规模为15-75的最优解及各项指标值；②通过双目标调节系数λ可以平衡平台收益与分配方案的鲁棒性，随着λ值的增大，平台收益分段增加，而鲁棒性分段下降；③基于特定算例，改变λ值求得最优解，筛选非支配解并拟合出近似帕累托前沿曲线，算例5-25中增加单位平台收益带来的鲁棒性的减少量的变化范围为［0.02，6.75］．

本研究方法可以在保证分配方案稳定运行的前提下，较好应对车辆提前到达或延迟离开所导致的不确定性，提高共享停车位预订与分配的合理性．今后研究内容可集中在非固定工作时间内的私人停车位共享问题，并设计计算效率更高的算法来求解大规模算例．