依赖借款方资产的还款方式中的自由边界问题

梁 进，张柳青

（同济大学数学科学学院，上海 200092）

贷款是银行的一种基本信用经济活动，银行通过贷款的方式将所集中的货币和货币资金投放出去，可以满足社会发展对资金的需要。同时，银行也可以由此取得贷款利息收入，增加自身的积累。贷款的还款方式主要有两种：等额本息还款和等额本金还款。韩慧丽［1］、杨玉国［2］、王顺［3］等人对两种还款方式进行了简单分析与比较，并给出了各自的适用人群。但这两种还款方式基本上都要求还款本息在还款期内均匀分布，银行可以由此确定未来的现金流，却没有给借款人更多的可以根据自身收入分布状况选择还款方式的余地。事实上，无论从借款人借款的初衷和银行最初设计贷款的本意来看，双方都希望能够按照合同规定的期限和利率按时足额偿还贷款本息［4］。

在助学贷款领域，经济学家Milton Friedman［5］于1955年首次提出了按收入比例还款型学生贷款（income-contingent repayment loan，以下简称ICL），其内涵主要是指接受高等教育的学生以毕业后收入的一定比例来偿还大学期间获得的现金支持。澳大利亚ICL的设计者Bruce Chapman［6］指出，ICL是一种在贷款的覆盖面、利率资助和回收机制等方面均优于传统定期定额贷款的新型贷款方案。到目前为止，ICL已经在世界多国广泛应用，逐步发展了以澳大利亚模式、英美模式与德国混合型模式为代表的ICL经典模式。刘丽芳［7］、冯涛［8］等学者立足我国1999年以来一直实行按揭型助学贷款的背景，分析了ICL在我国的可行性，并设想了适合中国国情的ICL方案。

ICL最显著的特点是“偿还额度是学生未来收入的函数［9］”。基于此，梁进和刘兆雅［10］将ICL的思想应用到了更加一般的贷款形式中，具体提出了依赖借款方资产的灵活还款方式和模型：在假定借款方资产满足随机过程的基础上，建立了借款方每期偿还当期资产固定比例的数学模型，并求解得到了模型的解析解。相比于传统还款方式中每期偿还固定的金额，这种还款方式大大降低了借款方违约的可能性。对于银行而言，借款方在资金充裕时多还款可以加速银行的资金回流，而在资金紧张时不违约，则可以取得更多的利息收入。

然而当借款方资产长期处于一个较低水平时，还款额就会十分有限，无形之中可能会拉长还款期限，从而影响银行的资金流动。梁进和毛家琪［11］在刘兆雅模型的基础上为定期还款额设置了一个下界，同时还款方式保持不变。而一旦定期还款额碰到下界则贷款立刻终止，借款方随即将当时所有资产用于偿还剩余贷款，这样既保障了借款方可以灵活还款，同时也在一定程度上确保了还款期限不会被无限拉长。但由于剩余贷款价值和借款方资产并没有直接联系，清算时将借款方全部资产用于偿还可能还多或还少，会对借贷双方造成损失。

本文在刘兆雅和毛家琪的研究基础上，进一步修正和推广了上述模型，从而为这种还款方式在未来贷款业务中发挥广泛作用提供了可能。具体而言，本文将绕过借款方资产而直接对剩余贷款价值设置下障碍。类似于美式期权，一旦剩余贷款价值达到下障碍，贷款立刻终止，借款方随即偿还剩余贷款进行清还。另外，考虑到当借款方资产处于较高水平时，还款额也较高，不会使得还款时间延长，因此本文首先将借款方资产划分为高资产以及低资产两个区域，并在两个区域中设定不同的还款条款，最终建立关于剩余贷款价值的带限制的自由边界问题模型。该模型的设定可以在减小借款方定期还款压力，降低违约可能性的同时，加快贷款方资金回收，进而保护贷款方的利益，从而对借贷双方都有很强的吸引力。

1 模型的建立

1.1 基本假设与符号

（4）给定常数下障碍水平d(d＜Q)，同时记Φ(S，t)为t时刻借款方资产St＝S时的剩余贷款价值，则Φ(S，t)满足初始条件，即

（5）借款方不违约，期望意义下在T时刻还清贷款。进一步假设借款方资产St≥d，以确保在还清时刻借款方可以足额偿还。

（6）（资产边界）设定资产边界K＝qd/δ＞d，将借款方资产划分为低资产区域{St：d≤St＜K}和高资产区域{St：St≥K}。

（7）（还款条款）在高资产区域内，借款方正常还款。但在低资产区域内，一旦剩余贷款价值等于d，或者借款方资产降为d，则贷款随即终止，借款方均立刻偿还d。

在假设（5）中，T的含义是指[0，T]时间内借款方还款总额贴现价值的期望等于贷款金额Q，即T满足初始条件（1），下文称T为期望还清贷款时间。T事先未知，求解T的过程分为两步：首先给定T，在特定的还款条款下求解Φ(S，t；T)的终值问题，随后根据初始条件（1）尝试确定T。在文献［10-11］中，根据不同的还款条款，条件（1）分别为

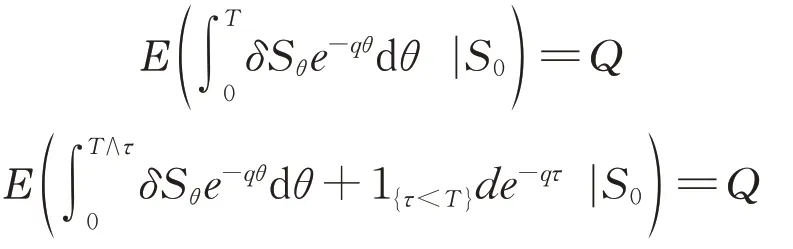
1.2 现金流分析

根据资产的划分，在低资产以及高资产两个区域内，首先将剩余贷款价值Φ(S，t)分别记为ΦL(S，t)与ΦH(S，t)。当借款方资产处于低资产区域时，根据假设（7），剩余贷款价值ΦL(S，t)始终大于等于d。当剩余贷款价值ΦL(S，t)大于d时，它在未来有4种可能：第1种在期望还清贷款时间T之前，由于资产进入高资产区域，剩余贷款价值ΦL(S，t)变为一份虚拟高资产区域中的剩余贷款价值ΦH(S，t)；第2种在期望还清贷款时间T之前，剩余贷款价值ΦL(S，t)已经达到d，贷款提前终止；第3种在期望还清贷款时间T之前，由于资产变为d而使贷款提前终止；第4种则是在期望还清贷款时间T之前，不发生第1～3种情况，剩余贷款价值ΦL(S，t)在T时刻达到d。

由此，定义如下3个随机变量τ1、τ2与τ3，分别表示借款方资产首次由低资产区域进入高资产区域时刻、剩余贷款价值ΦL(S，t)首次达到d时刻以及资产首次达到d时刻。

当借款方资产处于高资产区域时，剩余贷款价值ΦH(S，t)在未来有2种可能：第1种在期望还清贷款时间T之前，由于资产进入低资产区域，剩余贷款价值ΦH(S，t)变为一份虚拟低资产区域中的剩余贷款价值ΦL(S，t)；第2种在期望还清贷款时间T之前，资产始终处于高资产区域，剩余贷款价值ΦH(S，t)在T时刻达到d。

同理，定义借款方资产首次由高资产区域进入低资产区域时刻τ4如下：

则高资产区域中的剩余贷款价值ΦH(S，t)可以表示为如下条件期望：

1.3 模型推导

基于上述现金流表达式，下文将推导在低资产区域以及高资产区域内，剩余贷款价值分别满足变分不等式和偏微分方程，而在资产边界K处，通过引入一阶导数连续条件使得模型具有唯一解。

1.3.1 低资产区域

在低资产区域中，根据贷款执行情况可将剩余贷款价值ΦL(S，t)分为以下两个部分：

（1）继续还款区域：Σ1＝{(S，t)∈[d，K)×[0，T]|ΦL(S，t)＞d}.

（2）贷款结束区域：Σ2＝{(S，t)∈[d，K)×[0，T]|ΦL(S，t)＝d}.

而在贷款结束区域Σ2内，剩余贷款价值为d，则ℒΦL+δS＝δS-qd＝δ(S-K)＜0。因此在低资产区域内，剩余贷款价值ΦL(S，t)满足

在边界S＝d处，由模型假 设（7），ΦL(d，t)＝d，表示当借款方资产降为d时，贷款随即终止，借款方立刻一次性偿还d。相比于文献［11］中的情形，由于ΦL(S，t)≥d，此时借款方只可能少还而不会多还剩余贷款，进而一定程度上保证了借款方的利益。

综上讨论，在低资产区域中，剩余贷款价值

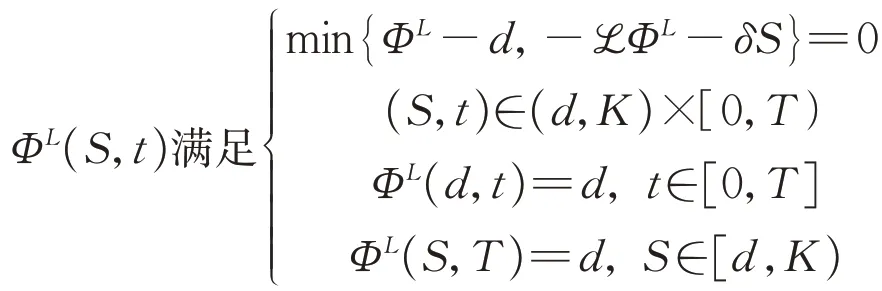
1.3.2 高资产区域

1.3.3 带限制的自由边界问题模型

在资产边界K上，根据现金流表达式（2）和式（3），有

根据上述讨论，若剩余贷款价值ΦL(S，t)与ΦH(S，t)均足够光滑，则它们是如下耦合问题的

由偏微分方程的理论可知，耦合问题（4）解存在但不唯一，因为在资产边界K处的条件仅为ΦL(K，t)＝ΦH(K，t)，想要得到唯一解必须在资产边界K处添加新的条件。注意到障碍问题的解一般具有连续的一阶空间导数［13］，以及线性抛物型方程的解具有无穷次可微性［14］，因此考虑在资产边界K处添加一阶导数连续条件。根据文献［15-16］中的讨论，利用Δ-对冲方法可以得到在等价鞅测度下成立。

因此，在资产边界K处也添加上述一阶导数连续条件。综上所述，若剩余贷款价值ΦL(S，t)与ΦH(S，t)均足够光滑，则它们是如下适定耦合问题的解：

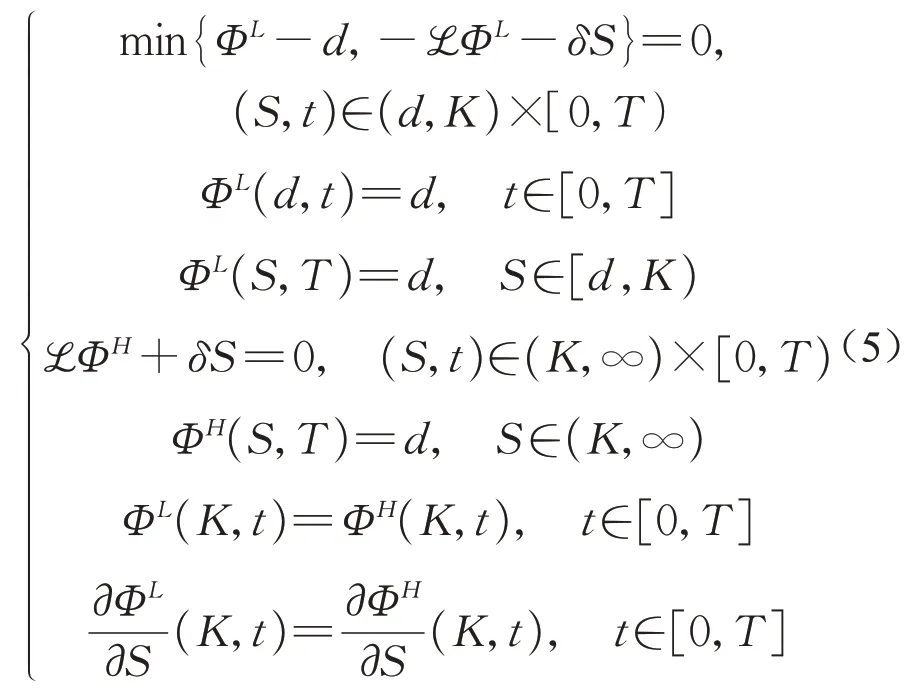
这是一个带限制的自由边界问题，确切地说是一个固定边界与自由边界问题相耦合的偏微分方程组问题。剩余贷款价值在低资产区域内满足变分不等式，在高资产区域内则满足偏微分方程，并且剩余贷款价值在跨过资产边界K时函数值以及一阶导数均连续。

2 数值计算与分析

利用有限差分法［18］首先在给定T的情况下计算剩余贷款价值Φ(S，t；T)，随后在低资产区域内计算自由边界。最后基于初始条件（1）：Φ(S0，0；T)＝Q，运用打靶法［19］求解期望还清贷款时间T，并讨论期望还清贷款时间与模型参数之间的关系。

2.1 有限差分法

运用有限差分法中的显式格式对剩余贷款价值Φ(S，t)进行数值求解，计算如下：

2.2 剩余贷款价值及自由边界

根据模型假设δ＜q以及充分条件（6），如无特殊声明，取模型参数和人工边界Smax如下：

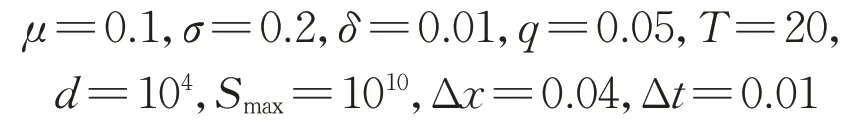
则资产边界K＝qd/δ＝5×104，低资产区域为{St：104≤St＜5×104}，以及高资产区域为{St：5×104≤St≤1010}。在图1a和图2中可以看到低资产区域内的剩余贷款价值被自由边界分为两部分：贷款结束区域和继续还款区域。剩余贷款价值在穿过自由边界时发生明显变化，而自由边界则具有一定的单调性和凸性。类似于美式期权，此时自由边界也可视为贷款的最佳还款边界。根据图1b，在高资产区域中，剩余贷款价值则始终大于d，直到期望还清贷款时刻等于d。

图1 给定T=20，高低资产区内剩余贷款价值Fig.1 The remaining loan value in high and low asset regions(Given T=20)

图2 给定T=20，低资产区域内的自由边界Fig.2 Free boundary in low asset region(Given T=20)

2.3 打靶法

应用打靶法求解期望还清贷款时间T：即首先给定T，接着通过有限差分法以及插值技巧计算Φ(S0，0；T)并与贷款金额Q相比较，最后寻找合适的T使得初始条件Φ(S0，0；T)＝Q在一定误差范围内成立。注意到在有限差分法计算过程中，剩余贷款价值Φ(S，t；T)关于T单调递增。因此，期望还清贷款时间T如果存在则必唯一。

2.4 期望还清贷款时间

同2.2节中的参数取值，另外根据模型假设S0＞Q＞d，在高低资产区域中分别取借款方初始资产S0和贷款金额Q如下：

高资产区域中S0＝106，Q＝5×105，低资产区域中S0＝4×104，Q＝2×104。

2.4.1 期望还清贷款时间与贷款金额的关系

低资产区域中取Q∈[1.1×104，3.9×104]，高资产区域中取Q∈[105，9×105]。从图3可以看出，在其他参数一定的条件下，无论借款方初始资产处于低资产区域还是高资产区域，期望还清贷款时间都随着贷款金额的增加而变长。这说明贷款金额越大，借款方的还款能力相对越低，还清贷款的时间也就越长。

图3 高低资产区域内期望还清贷款时间T与贷款金额Q的关系Fig.3 The relationship between the expected clear off time and loan amount in high and low asset regions

2.4.2 期望还清贷款时间与借款方初始资产的关系

低资产区域中取S0∈[2.1×104，4.9×104]，高资产区域中取S0∈[6×105，106]。从图4可以看出，在其他参数一定的条件下，无论借款方初始资产处于低资产区域还是高资产区域，期望还清贷款时间都随着初始资产的增加而变短。这说明借款方初始资产越多，还款能力相对越强，还清贷款的时间也就越短。

图4 高低资产区域内期望还清贷款时间T与借款方初始资产S0的关系Fig.4 The relationship between the expected clear off time and initial asset of the borrower in high and low asset regions

2.4.3 期望还清贷款时间与借款方资产期望收益率的关系

在两个区域中，均取μ∈[0.055，0.3]。从图5可以看出，在其他参数一定的条件下，无论借款方初始资产处于低资产区域还是高资产区域，期望还清贷款时间都随着借款方资产期望收益率的增加而变短。这说明资产期望收益率越大，借款方资产经营情况越好，因而还款能力相对越强，还清贷款的时间也就越短。

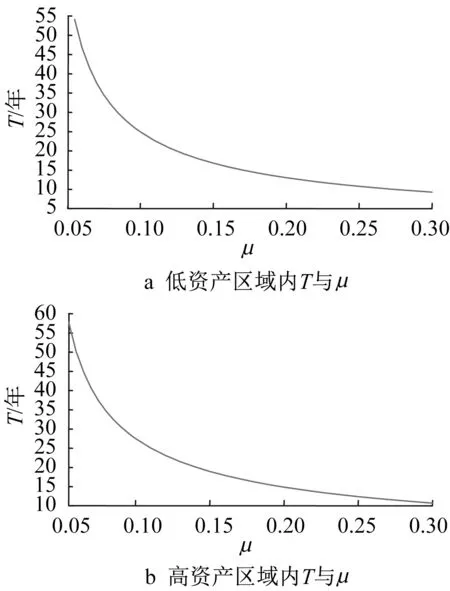
图5 高低资产区域内期望还清贷款时间T与借款方资产期望收益率μ的关系Fig.5 The relationship between the expected clear off time and the expected rate of return on borrower's asset in high and low asset regions

2.4.4 期望还清贷款时间与借款方资产波动率的关系

在两个区域中，均取σ∈[0.06，0.6]以及Δx＝0.04，Δt＝0.001。从图6可以看出，在其他参数一定的条件下，当借款方初始资产处于低资产区域时，期望还清贷款时间随着借款方资产波动率的增加而变短。这说明资产波动率越大，借款方资产变化越大，但由于此时资产St有下界d，因此资产变化带来的影响是不均等的，借款方的还款能力相对越强，还清贷款的时间也就越短。而当借款方初始资产处于高资产区域时，期望还清贷款时间则随着借款方资产波动率的增加而变长。这说明资产波动率越大，借款方资产变化越大，而且资产降低带来的影响超过了上升的影响，即资产越可能进入低资产区域，因此借款方的还款能力相对越低，还清贷款的时间也就越长。

图6 高低资产区域内期望还清贷款时间T与借款方资产波动率σ的关系Fig.6 The relationship between the expected clear off time and the volatility of the borrower's asset in high and low asset regions

2.4.5 期望还清贷款时间与贷款利率的关系

在两个区域中，均取q∈[0.045，0.1]。从图7可以看出，在其他参数一定的条件下，无论借款方初始资产处于低资产区域还是高资产区域，期望还清贷款时间都随着贷款利率的增加而变长。这说明贷款利率越大，借款方还款额的贴现价值越小，因此还款能力相对越低，还清贷款的时间也就越长。

图7 高低资产区域内期望还清贷款时间T与贷款利率q的关系Fig.7 The relationship between the expected clear off time and lending interest rate in high and low asset regions

2.4.6 期望还清贷款时间与还款强度的关系

低资产区域中取δ∈[0.004，0.012]，高资产区域中取δ∈[0.004，0.045]。从图8可以看出，在其他参数一定的条件下，无论借款方初始资产处于低资产区域还是高资产区域，期望还清贷款时间都随着还款强度的增加而变短。这说明还款强度越大，借款方连续还款额也越大，还款能力相对越强，还清贷款的时间也就越短。

图8 高低资产区域内期望还清贷款时间T与还款强度δ的关系Fig.8 The relationship between the expected clear off time and repayment intensity in high and low asset regions

2.4.7 期望还清贷款时间与下障碍水平的关系

低资产区域中取d∈[8.5×103，1.95×104]，而在高资产区域中取d∈[5×103，8×104]以及Δx＝0.0075，Δt＝0.001。从图9可以看出，在其他参数一定的条件下，无论借款方初始资产处于低资产区域还是高资产区域，期望还清贷款时间都随着下障碍水平d的增加而变短。这说明下障碍水平d越大，贷款相对能够越早的终止，还清贷款的时间也就越短。

图9 高低资产区域内期望还清贷款时间T与下障碍水平d的关系Fig.9 The relationship between the expected clear off time and the level of low obstacle in high and low asset regions

3 结语

本文继续探讨了一种依赖借款方资产的还款方式。为了尽可能缩短还款期限以保障贷款方的利益，本文首先设置资产边界将借款方资产分为低资产以及高资产两个区域，并在两个区域中设定不同的还款条款，数学上即是建立了关于剩余贷款价值的带限制的自由边界问题模型。接着，通过显式差分格式计算剩余贷款价值，并由此得到了相应的自由边界。最后，利用打靶法求解期望还清贷款时间，在一定的参数范围内讨论了模型参数对期望还清贷款时间的影响。

结果表明：无论借款方初始资产处于低资产区域还是高资产区域，期望还清贷款时间T都随着借款方初始资产S0、资产期望收益率μ、还款强度δ和下障碍水平d的增大而变短，以及随着贷款金额Q和贷款利率q的增大而变长。另外，在低资产区域中，期望还清贷款时间T随着借款方资产波动率σ的增大而变短，而在高资产区域中则相反。

作者贡献声明：

梁进：提出研究选题与模型，研究思路、写作指导。

张柳青：负责模型推导、数值计算、论文撰写等工作。