基于纯电动汽车高频数据的驾驶风格分类方法
2022-03-22纪少波苏士斌何绍清冯远宏
纪少波,张 珂,李 伦,苏士斌,何绍清,冯远宏,张 强
(1.山东大学能源与动力工程学院,山东济南 250061;2.青岛海信网络科技股份有限公司,山东青岛 256000;3.中国汽车技术研究中心有限公司,天津 300300)
根据国家统计局2013—2020年发布的《中国统计年鉴》,我国道路安全事故发生情况可以看出近几年的车祸发生数量呈增长趋势,这表明交通安全问题日渐严重。驾驶员作为交通行为的首要执行者、车辆的操控者,是导致交通事故的主要原因。因此,驾驶员在行驶过程中驾驶行为的安全性具有重大的研究价值。
国内外学者多采用无监督学习模型进行驾驶风格分类,通过对分类结果的分析确定驾驶风格类别。目前研究驾驶风格用的无监督学习主要有基于划分、层次、密度及模型等不同方法的聚类方法。基于划分的无监督学习聚类方法主要有K均值(Kmeans)和模糊C均值(FCM)。亓航等[1]、徐婷等[2]和余荣杰等[3]研究学者采用K均值聚类算法分别对出租车、货车和分时租赁汽车的驾驶行为数据进行驾驶风格分类,发现不同驾驶风格的驾驶员在出行特点、车辆运行参数及百公里能耗方面都具有差异性。石秀鹏等[4]从车辆轨迹数据提取了风险指标特征,基于这些特征利用FCM算法将驾驶行为聚为4个风险等级。基于层次的无监督学习聚类方法主要是层次聚类算法,牛增良等[5]基于大量重特大交通事故数据采用模糊聚类、层次聚类对危险驾驶行为划分层次进行分析。基于密度的无监督学习聚类方法主要是密度聚类(DBSCAN)算法,文江辉[6]从营运车辆监控平台获取出行高频时间段的车辆运行数据,利用DBSCAN算法对不同车辆、不同时间段及不同天气状况下驾驶行为进行了分类,用于判定车辆驾驶的稳定性程度。基于模型的无监督学习聚类方法主要是利用高斯混合模型(GMM)等模型展开研究,朱冰等[7]基于真实驾驶数据采用GMM和KL散度定量地度量驾驶员之间的相似性,实现驾驶员驾驶风格分类。李立治等[8]建立了驾驶员驾驶风格的数据库,使用K均值、FCM及层次聚类对驾驶风格进行分类。李卓轩等[9]基于不良驾驶行为特征参数,使用K均值聚类和DBSCAN算法对驾驶风格进行分类。刘通等[10]基于K均值聚类算法进行了驾驶风格的分类研究。
已有研究采用的聚类算法多是针对低维数据集设计的,处理高维数据集通常会面临“维灾难效应”,会出现基于距离的度量函数失效、聚类中心难以确定及计算效率低等问题。本文采用先降维后聚类的研究思路,在对比不同降维及聚类方法的基础上,提出利用t-SNE和GMM组合算法建立基于驾驶安全的驾驶风格分类模型,用于对不同驾驶风格进行分类。此外,已有研究关于异常驾驶行为的判定多采用固定阈值,本文在深入分析与驾驶安全相关的特征参数变化规律基础上,提出多参数组合阈值边界线识别危险驾驶行为的方法。本文的研究可以有效改进分类效果,提高异常驾驶识别精度。研究内容可为运输企业的安全运营提供指导,为道路安全评估提供参考。
1 数据采集与处理
1.1 数据采集
基于车辆的OBD接口,通过CAN总线获取车辆实时运行数据,并将采集的数据通过无线网络发送至服务器进行处理,数据采集流程如图1所示。驾驶员瞬态操作数据中包含丰富的驾驶行为信息,过低的采样频率将导致瞬态驾驶行为信息丢失;过高的采样频率将导致数据采集成本增加,数据处理难度加大,因此需要合理选择监测频率。心理学家认为正常人的反应时间为0.15~0.4s,最快反应时间也高于0.1s。本文数据采集频率设置为10 Hz,即采集间隔为0.1s,采样频率完全可以满足驾驶行为分析需求。

图1 车辆监测数据采集流程Fig.1 Vehicle monitoring data collection process
本文研究数据主要来自于北京、成都、天津、上海四座城市的200辆纯电动汽车4个月的高频运行数据,汽车用途有私家车、网约车、共享汽车。数据样本具有采样频率高、车辆用途多样、驾驶员分布广泛、出行次数频繁等优点,适用于驾驶员的驾驶行为分析。
1.2 数据处理
由于原始数据是按车辆VIN码分类储存的,且采集信号中存在的无效数据字段导致原始数据体量巨大,影响后续研究。因此,本文首先剔除了无效字段信号数据和充电与静置片段数据,形成每车每次独立的运行数据文件。考虑到一次正常行车时长不会过短,且驾驶工况在较短时间内变化不会很大,所以结合车辆的上电状态及车速,剔除一次行车时长小于10min和数据缺失率超过5%的行程事件。处理后的一次行车事件数据如图2所示。

图2 一次行车事件数据Fig.2 Data in a driving event
数据采集和传输过程受到干扰可能导致远程数据管理平台接收到的数据存在波动、异常或缺失等问题。为了消除异常数据的影响,在进行数据分析前需要对原始数据进行质量控制。首先对于轻微波动的信号数据采用滑动窗口均值滤波方法进行处理,效果如图3所示。采用统计分析和6σ法去除幅值异常的数据点;接收的数据中存在相邻数据时间差小于采样时间的问题,这主要是由于网络不稳导致数据重复发送造成,将这些冗杂数据亦作为异常值剔除,处理后的效果如图4所示。此外,对少量的缺失数据值采用线性插值进行填补。
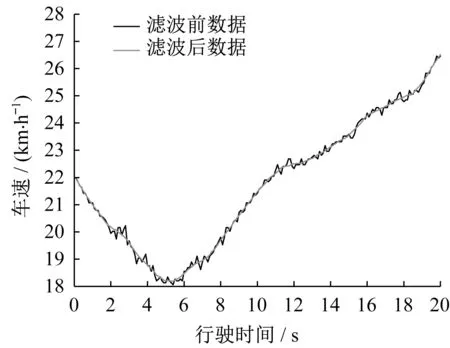
图3 滤波前后数据对比Fig.3 Comparison before and after treatment of filter

图4 异常值处理效果Fig.4 Treatment of abnormal value
在对原始数据进行质量控制后,参考文献[11-14]选取与驾驶安全有关的驾驶行为特征参数表1所示。通过对事故发生原因的分析,驾驶员超速、急加速、急减速和急转向等危险驾驶行为是导致事故多发的重要原因[15]。但在我国现有的相关交通规定中未对这些危险驾驶行为进行约束,并且交通违章监控难以有效辨识,无法及时给予驾驶员危险警示以避免事故的发生。本文对急加速、急减速、超速、急转向、转向超速和疲劳驾驶等不同危险驾驶行为的判别方法进行了研究。

表1 驾驶行为特征参数Tab.1 Driving behavior characteristic parameters
1.2.1 急加速
对车辆速度与前向加速度参数进行分析得到图5。使用式(1)对前向加速度与速度关系中的各分位值进行线性拟合,结果如表2所示。

表2 前向加速度各分位值的拟合参数Tab.2 The fitting parameters of each quantile value of forward acceleration

图5 前向加速度分位值随速度变化关系Fig.5 The relationship between acceleration quantile value and velocity
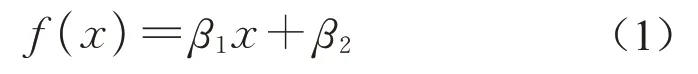
式中:x表示车辆速度;β1和β2是拟合参数;R2表示拟合系数。
文献[9]将最大加速度阈值设定为2.78m·s-2,文献[16-19]将最大加速度阈值设定为3m·s-2。由图6可知,前向加速度的峰值随速度增加呈降低的趋势,因此,如果将最大加速度阈值设为固定值,无法准确反映车辆实际运行情况。为此本文提出了多参数组合阈值边界线进行危险驾驶行为识别的思路,即随着车速的变化,最大加速度阈值亦相应调整,根据前向加速度峰值随速度的变化规律,定义了急加速判断阈值边界线为第99%分位值,如图6所示。

图6 急加速判断阈值线Fig.6 The judgment threshold line of rapid acceleration
1.2.2 急减速
对车辆速度与制动减速度参数进行分析,各分位值结果如图7所示,由图可见,制动减速度在约25km·h-1时存在拐点,这是由于研究用车辆存在制动能量回收,在25km·h-1时有最大的制动回收力矩。制动减速度各分位值在速度超过100km·h-1变化幅度较小,使用式(2)对制动减速度分位值进行分段线性拟合,以速度值25km·h-1为线性拟合分段边界,结果如表3所示。

表3 制动减速度各分位值的拟合参数Tab.3 The fitting parameters of each quantile value of braking deceleration
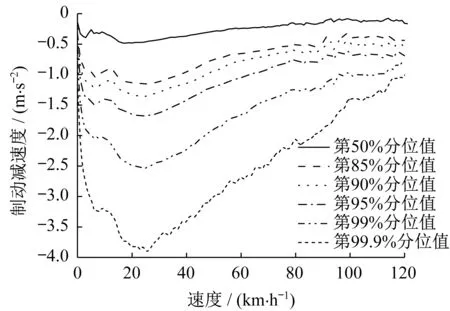
图7 制动减速度分位值随速度变化关系Fig.7 The relationship between braking deceleration quantile value and velocity
参考急加速阈值线设定,本文同样定义了急减速判断阈值线为第99%分位值,如图8所示。

图8 急减速判断阈值线Fig.8 The judgment threshold line of sharp deceleration

式中:x表示车辆速度;β1、β2、β3、β4是拟合参数;R2表示拟合系数。
1.2.3 超速
在不同的道路环境中限速是不同的,在城市道路中,车辆的限速一般为60km·h-1,高速道路中一般最高限速为120km·h-1。文献[20]认为车速在高于80km·h-1就认为驾驶员有超速倾向或已经在超速行驶了,而车速高于120km·h-1必然是超速行驶了。但准确的超速行驶行为的识别需要基于不同路段的限速情况进行,由于本文缺少道路限速信息,仅采用两个等级指标表征超速行为的严重程度:车速80~120km·h-1的行驶时间占总行驶时间的比例和车速高于120km·h-1行驶时间占总行驶时间的比例。
1.2.4 急转向
对车辆速度与方向盘角速度参数进行分析,各分位值结果见图9,随车速的增加,方向盘角速度持续降低,为此使用式(3)对方向盘角速度的各分位值进行曲线拟合,结果如表4所示。

图9 方向盘角速度分位值随速度变化关系Fig.9 The relationship between steering wheel angular quantile value and velocity

表4 方向盘角速度各分位值的拟合参数Tab.4 The fitting parameters of each quantile value of the steering wheel angular velocity

式中:x表示车辆速度;a、b、c是拟合参数;R2表示拟合系数。
同理,本文定义了急转向判断阈值线为第99%分位值,阈值线如图10所示。

图10 急转向判断阈值线Fig.10 The judgment threshold line of sharp turning
1.2.5 转向超速
对车辆速度与方向盘转角参数进行对比分析,各分位值结果见图11,使用式4对不同方向盘转角下的车速各分位值曲线进行拟合,结果如表5所示。

表5 车速各分位值拟合参数Tab.5 The fitting parameters of each speed quantile value

图11 车速各分位值随方向盘转角变化关系Fig.11 The relationship between speed quantile value and the steering wheel angle

式中:x表示方向盘转角;a、b、c是拟合参数;R2表示拟合系数。
同理,本文定义了转向安全车速分界线为第99%分位值,转向超速行为通过该分界线进行识别,如图12所示。

图12 转向超速判断阈值线Fig.12 The judgment threshold line of overspeed while turning
1.2.6 疲劳驾驶
统计结果表明疲劳驾驶造成的交通事故占事故总数的20%左右,占特大交通事故总数的40%以上[21]。行车时长是影响疲劳驾驶的直观因素,本文将单次行车累计时长超过4h记为疲劳驾驶。
2 驾驶风格分析
2.1 高斯混合模型
在聚类算法中K均值聚类算法因原理易懂、收敛速度快的优点得到广泛应用。但K均值聚类算法结果受初始聚类中心影响非常大,而且其要求簇的形状必须是圆形的,若实际样本点是椭圆分布的,其聚类结果可能会出现多个圆形的簇混在一起,聚类效果差。高斯混合模型(GMM)可以弥补K均值聚类算法的不足,GMM未将每个样本点置于明确簇中,而给出了该样本点在各簇中的概率或可能性,因此能够有效避免硬分配,并且簇的形状可以是任意椭圆状,而不仅局限于圆形。
假设数据集X={x1,x2,…,xn}服从由K个多元高斯分布组成的GMM,即可分为K类。对于每个样本xi,高斯混合分布的概率密度函数为
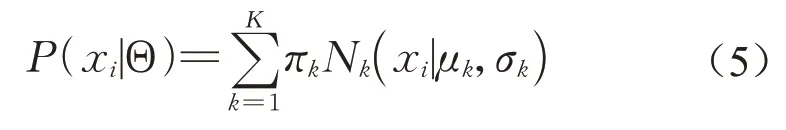
式中:πk是混合系数;μk,σk为每个高斯成分的均值和方差。Nk(xi|μk,σk)为第k个高斯成分的概率密度函数,即xi属于第k类的概率,可表示为

使用期望最大化(EM)算法对GMM进行非线性概率函数的优化。首先根据类别数目设定模型参数初值(μ0k,σ0k),迭代多次求出参数(μk,σk),即每一个样本属于第k类的概率,由最大后验概率准则可知,后验概率最大的那项类别为该样本所属聚类结果[22]。
2.2 降维方法选择
为了避免高维数据集导致的“维灾难效应”,在利用聚类算法进行驾驶风格分类时需要提前对驾驶行为数据集进行降维处理。常见的降维方法有多维尺度分析(MDS)、主成分分析(PCA)、等距特征映射(ISOMAP)和t分布随机邻域嵌入(t-SNE)等[23-24]。文献[24]指出在处理不同的高维数据集时,需要针对数据集特点选择适合的方法。因此本文采用PCA、MDS、t-SNE和ISOMAP 4种降维方法分别对驾驶风格特征参数进行降维,再将降维结果分别输入GMM算法中进行驾驶风格聚类。不同降维方法的效果采用轮廓系数S进行对比。
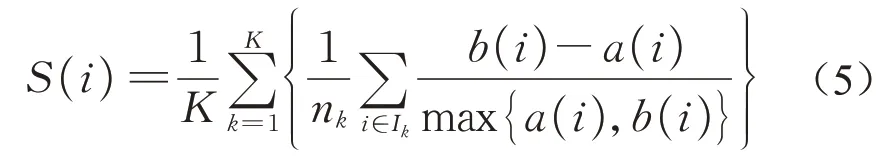
式中:K表示分类数量;nk表示第k类的观测值总数;a(i)是观测值xi与所在第k类其他值的平均距离;b(i)是观测值xi与其他集群中所有值的平均距离中最小值;Ik表示第k类集群观测值的索引集。
本文基于驾驶风格特征参数数据集比较了不同K取值的轮廓系数,确定最佳聚类K值,由图13可知将驾驶风格特征参数为3类效果最好。
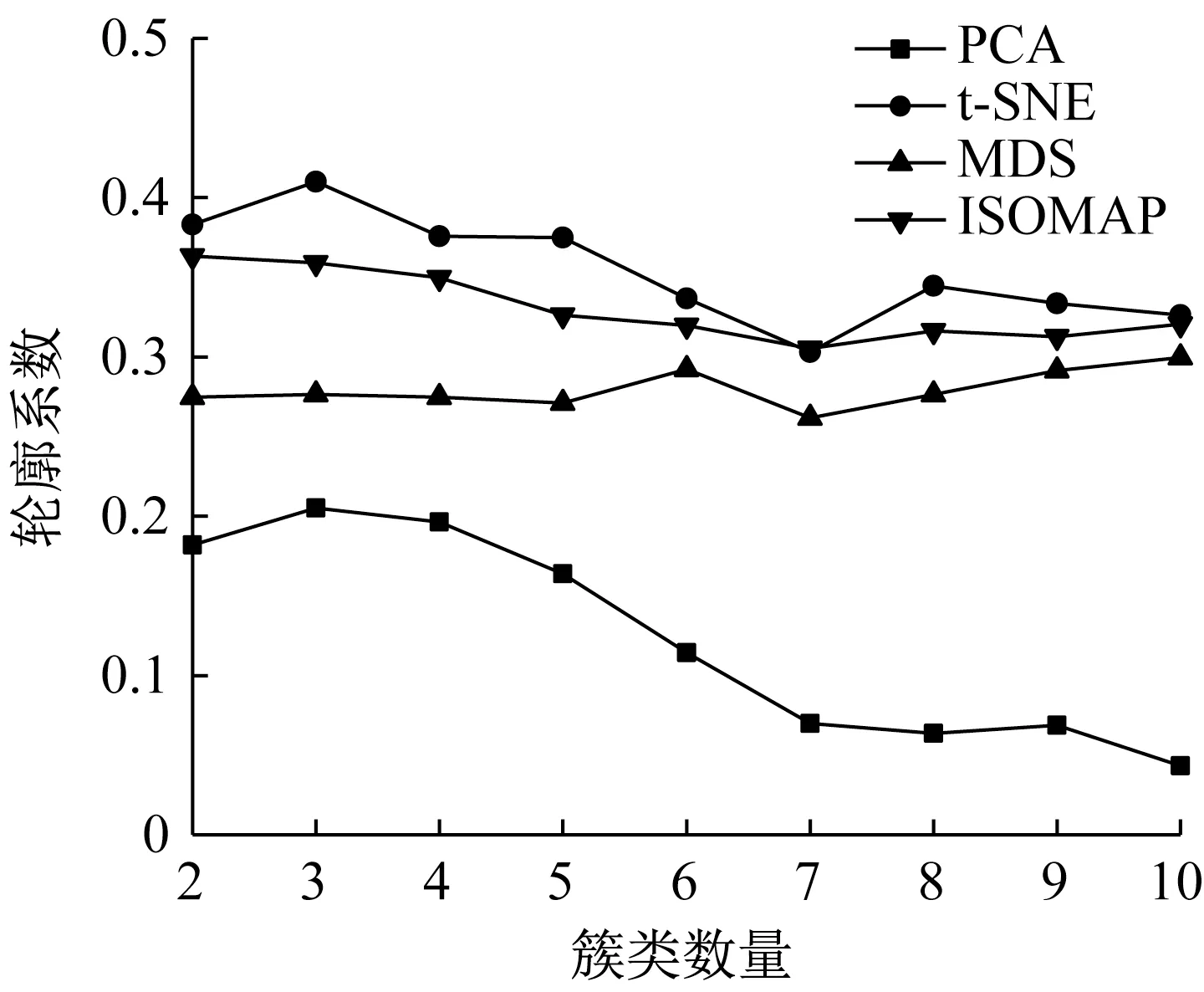
图13 不同K取值的轮廓系数Fig.13 Silhouette coefficient with different values of K
将上述降维方法结合K均值聚类算法和GMM两种聚类算法进行聚类效果的对比,结果如表6所示。结果表明对于本文所用驾驶风格数据集而言,相对于K均值聚类算法,GMM与每种降维方法组合后普遍表现出更优的聚类效果,且t-SNE和GMM组合聚类方法的轮廓系数最高。因此,本文最终选择t-SNE和GMM算法把驾驶风格特征参数数据集聚为3类驾驶风格。

表6 不同降维与聚类算法聚类效果Tab.6 Clustering effect of different dimension reduction and clustering algorithms
2.3 驾驶风格分类结果分析
驾驶行为是指驾驶员在某一次驾驶过程具体的操作行为,驾驶风格是指驾驶员在驾驶时所表现的综合行为特征,也是驾驶员养成的基本固定的驾驶习惯。也就是说驾驶行为能够反映驾驶风格,驾驶风格从一定程度上决定驾驶行为。为了揭示3种不同驾驶风格对应的车辆运行特征,本文从监测数据服务器接收的私家车与网约车数据中,提取同一款纯电动车型30名驾驶员一个月的驾驶事件(共2 227次)对应的驾驶数据。运用t-SNE算法对驾驶数据进行降维,采用GMM算法对降维后数据进行驾驶风格分类,聚类效果如图14所示,分类结果中各特征参数的平均值如表7所示。

图14 驾驶风格聚类效果Fig.14 Clustering effect of driving style
根据表7中各类特征参数平均值结果,发现第1类样本的百公里急加/急减/急转向/转向超速次数、加(减)速度平均值与标准差都是3类中最高的,而这些参数都与驾驶粗暴相关,故推断第1类为激进型风格;相对而言,第3类样本的车速、加(减)速度平均值与标准差都是3类中最低的,故推断第3类为保守型风格,推断第2类为普通型风格。保守型的平均速度比激进型低约15 km·h-1,这是因为保守型驾驶风格为确保行车安全,将车速稳定在安全车速以内。普通型驾驶风格也是熟练驾车人群常用的驾驶风格,保持速度稳定的能力较强,激进型驾驶风格对车速控制能力最差。图15为不同驾驶风格对应的危险驾驶行为发生次数对比结果,由图可见,激进型驾驶风格的危险驾驶行为在高发区间的占比最高。说明激进型对车辆控制能力最差,危险驾驶行为发生次数最多,发生交通事故的风险最高,对于这一类驾驶员群体,可针对性进行安全教育,提高驾驶员安全意识,减少交通事故伤亡和损失。相对而言,对于保守型驾驶风格而言,危险驾驶行为发生次数主要集中在低发区。普通型风格对应的危险驾驶行为发生次数介于保守型和激进型之间。不同风格驾驶员的车辆运行特性分类结果也验证了本文提出的分类算法是有效的。
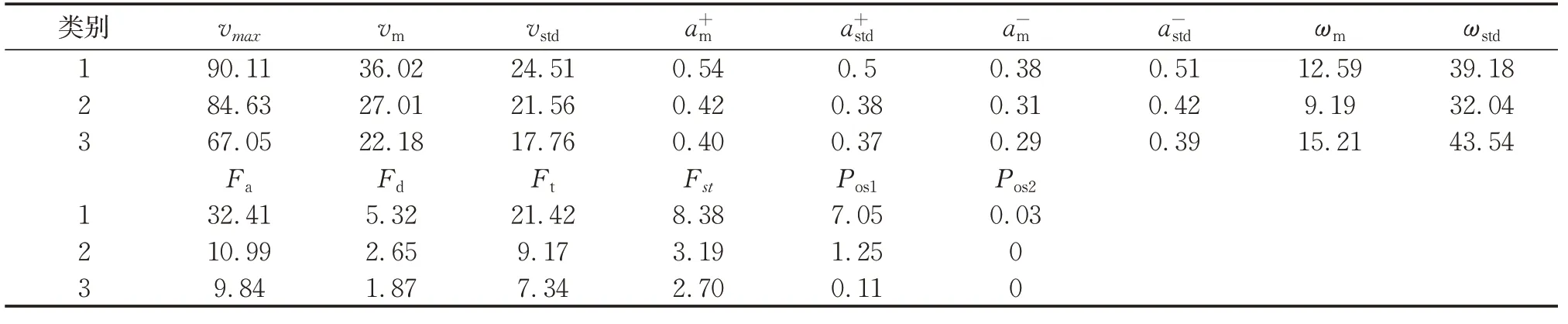
表7 各类特征参数平均值Tab.7 Average value of various characteristic parameters

图15 危险驾驶行为发生次数分布情况Fig.15 Distribution of the occurrence times of dangerous driving behavior
3 结论
为提高驾驶员安全认知,探究驾驶风格划分方法,本文利用纯电动汽车高频运行数据开展研究工作,主要结论如下:
(1)对驾驶行为数据进行统计分析,根据分析结果提出了采用多参数组合阈值边界线进行异常驾驶行为的识别,并得到了不同驾驶行为特征参数的危险驾驶阈值边界线。
(2)选取了15个与驾驶安全有关的驾驶风格特征参数,对多参数降维及聚类算法进行研究,通过轮廓系数对2种聚类算法和4种降维方法的性能进行评价,结果表明t-SNE和GMM组合算法分类效果最好。
(3)以t-SNE和GMM组合算法建立了基于驾驶安全的驾驶风格分类模型,将驾驶风格分为3种类型,不同驾驶风格对应的车辆运行特性分析结果验证了分类算法的有效性。
作者贡献声明:
纪少波:论文研究思路提出及语言组织。
张珂:车辆运行特性统计分析。
李伦:驾驶风格分类方法对比。
苏士斌:试验样本方案制定。
何绍清:车辆运行数据采集。
冯远宏:数据接收方法研究。
张强:数据预处理方法研究。
