基于正交试验的机械密封螺旋槽参数优化研究*
2022-03-22王鸿江刘连强张家祥张金亚
王鸿江 刘连强 张家祥 张金亚
(1.中国石油大学(北京)机械与储运工程学院 2.北京航天石化技术装备工程有限公司)
0 引 言
机械密封是一种由动静环端面在介质压力、弹性补偿机构弹力以及辅助密封配合作用下,保持端面贴合并相对滑动达到密封效果的轴向端面密封方式,又称端面密封[1]。机械密封因其良好的密封特性而得到广泛应用,95%左右的化工旋转设备中采用机械密封来防止介质泄漏[2]。对于泵送螺旋槽型机械密封来说,稳定的间隙液膜可以保证密封长期运行,而螺旋槽型参数以及螺旋槽所处位置对于密封性能有很大的影响。为了提高机械密封性能,并进一步优化螺旋槽型参数,探索螺旋槽位置系数λ对机械密封空化的影响有着重要的意义。
在机械密封端面槽型优化设计方面,已有多位学者开展了相关研究并取得了一定的进展[3-8]。丁雪兴等[9]针对单列槽和人字槽2种不同槽形进行密封性能对比,表明人字槽上游泵送机械密封的动压效应及密封性能均优于单列槽,说明微间隙流动中,槽与槽之间的相互干渉作用明显。陈汇龙等[10]优化了螺旋角θ、槽深h、槽宽比γ以及槽径比β,经过遗传算法得到优化槽型:螺旋角θ取17°,槽深h为8.6 μm,槽宽比γ为0.56以及槽径比β为0.78,但其并未对螺旋槽位置参数λ进行探索。LI Z.T.等[11]对螺旋槽处在流道中部位置进行了空化试验研究,并未与传统泵入、泵出式机械密封进行对比。李振涛等[12]研究了槽深h为1~15 μm,槽数n为6~30,螺旋角θ为14°~21°以及槽径宽径比为0.1~1.0的端面空化效应,表明空化效应随槽深和槽数的增加而增强,随槽径比的增加呈现先增强、后减弱的趋势,但随螺旋角的增加而减弱。魏琳宗等[13]对静压式机械密封结构参数进行了优化设计,结果表明密封端面转折半径的位置对密封结果产生显著影响。马润梅等[14]等对密封性能参数进行了优化,但只局限于优化单一的工况点,在对多目标密封性能参数的优化过程中没有提出明确的优化评估指标。
目前,对于螺旋槽的结构参数优化大多着眼于槽型本身,对螺旋槽所处位置并未进行探索。机械密封结构优化方法中较为经典的为正交试验法[15]和多目标优化算法[16]。本文采用CFD方法对上游泵送机械密封进行数值模拟,基于正交试验法,以P(即泄漏量增量ΔQ/开启力增量ΔF)作为优化评价指标,提出最优工况曲线法,研究不同槽型结构影响下的液膜空化特性及密封性能。
1 物理模型
1.1 几何模型
螺旋槽几何模型如图1所示,分为槽区、堰区和坝区。槽型线采用对数螺旋线,公式如下:

图1 螺旋槽机械密封示意图
r=rieφtanθ
(1)
式中:ri为密封环内径,mm;φ为螺旋线展开角,(°);θ为螺旋角,(°);
为了提高螺旋线的精确度,采用MATLAB计算螺旋线坐标,采用文献[12]中参数,密封环外径ro=53.25 mm,槽底半径rg=50.55 mm,液膜厚度1.5 μm,槽径比β=0.7,内径ri=44.25 mm,槽数n=12,螺旋角θ=18°,槽堰比lg/lw=1,转速为2 970 r/min。为了简化运算,采用全流道的1/n进行数值模拟。内压pi(内径处)为0.1 MPa,外压po(外径处)为0.1 MPa,采用水为模拟介质,温度为300 K,饱和蒸汽压pc为4.25 kPa。
1.2 网格划分及边界条件
单周期螺旋槽网格划分策略如图2所示,为了方便查看,在液膜厚度方向上放大1 000倍。在槽区及2个半堰区采用三棱柱网格,可以很好地解决尖角处网格最大倾斜度过大的问题,在坝区采用四棱柱网格,在计算两侧周期性边界时防止网格差异过大造成计算误差过大。单周期模型的最大网格倾斜度都在0.8以下,可实现高质量网格划分要求。

图2 单周期螺旋槽网格划分策略
1.3 网格无关性验证
以不考虑液膜内发生空化效应,内外压均为0.1 MPa进行验证。采用gambit划分时,interval size对泄漏量Q的影响较大,所以在确定interval size的基础上调整膜厚及槽深方向的层数来改变网格数量。网格无关性验证结果如图3所示。由图3可知,网格数≥113 944时,泄漏量Q基本不变,此时采用液膜厚度方向为5层,槽深方向为14层网格,与文献[17]相符。为提高计算效率,采用网格数为11万左右进行计算。

图3 网格无关性验证
1.4 文献验证
为验证上述方法的正确性,采用文献[12]中的槽型参数及工况参数进行验证,不考虑液膜间隙发生空化效应,结果如图4所示。

图4 文献验证
由图4可以看出,模拟结果与文献[12]结果非常接近,可以开展后续研究。
2 空化模型及控制方程
2.1 空化模型
Fluent中提供了3种多相流模型,分别为VOF(Volumeof Fluid)模型、混合(Mixture)模型和欧拉(Eulerian)模型。密封间隙的空化由螺旋槽底部的局部低压产生,故选择Mixture模型更合适。在Mixture模型中提供了3种空化模型,Singhal et al.模型不易收敛,Schnerr and Sauer 模型和Zwart-Gerber-Belamri模型结果基本相同,且在数值上更精确,收敛更快,本文与文献[12]选择一致,即采用Schnerrand Sauer模型[12,18]。
2.2 控制方程
基于空化的连续性方程、动量方程及气相传输方程如下[19]:
(2)
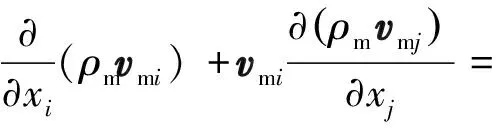

(3)
(4)
其中:
ρm=αρv+(1+α)ρl
(5)
μm=αμv+(1-α)μl
(6)
式中:ρm为混合物密度,vm为质量平均速度,μm为混合黏性系数,Re、Rc分别为气泡产生和溃灭源项,下标m为相数,下标v为气相,下标l为液相,α为气相体积分数。
3 正交试验设计
文献[10,12]中优化前与优化后的槽宽比γ取值差别不大,故本文中槽宽比γ取0.5。引入螺旋槽的位置系数λ,即槽底半径与端面内半径之差与坝区径向距离的比值,公式如下:
(7)
可得螺旋槽的槽底半径rgi(见图5)为:
rgi=(ro-ri)(1-β)λ+ri
(8)


图5 螺旋槽机械密封示意图(螺旋槽位置发生变化时)
螺旋槽结构参数中,槽深h、槽径比β、螺旋角θ、槽数n及螺旋槽位置系数λ的正交试验五水平取值如表1所示。

表1 各因素水平取值
4 结果与分析
4.1 正交试验计算分析
基于正交试验表进行数值模拟,计算25组工况下的泄漏量、开启力F及气相体积分数α(气相体积占液膜总体积的比值),结果见表2。


表2 正交试验结果
通过计算可得各因素的泄漏量对应的rj值,进行比较得到:rE>rD>rB>rA>rC,说明各因素对泄漏量影响的主次顺序为:λ>n>β>h>θ。只考虑泄漏量时,最佳参数组合方案为E5D3B1A4C5。同理,得到各因素开启力对应的rj值进行比较得到:rE>rD>rC>rB>rA,说明各因素对开启力影响的主次顺序为λ>n>θ>β>h。只考虑开启力时,最佳参数组合方案为E1D4C2B3A3。两者综合分析表明:螺旋槽位置系数λ对密封性能影响最大,槽数n的影响次之。螺旋槽位置系数λ对泄漏量和开启力的极差比其他因素对应的rj大得多。
为了探究螺旋槽位置系数λ对密封性能参数的影响,发现当槽位系数λ逐渐增大时,密封间隙内的气相体积分数也呈增大趋势,在λ=0.5左右达到峰值,如图6所示。

图6 气相体积分数α随槽位系数λ的变化曲线
为进一步探究密封端面空化对密封性能参数的影响,分别绘制了泄漏量Q随气相体积分数变化的散点图及开启力F随气相体积分数变化的散点图,如图7所示。从图7可见:当螺旋槽位置系数λ=0时,即为泵出型结构时,气相体积分数基本低于20%,开启力大于400 N,泄漏量大于5 mg/s;当螺旋槽位置系数λ≠0时,密封间隙内发生强烈的空化,气相体积分数增大,液膜内的压力下降,导致开启力和泄漏量迅速减小,螺旋槽的性能会发生突变。同时,从散点图中易知,密封性能参数随气相体积分数变化大致呈指数关系。由于剧烈的空化导致密封环不稳定运行,出于运行安全考虑,优化结构选择气相体积分数较低的泵出型开槽形式,即选择E1。

图7 密封性能参数随气相体积分数α变化的散点图
4.2 多目标参数最优工况曲线分析
提出多目标最优工况曲线法,找出一系列在不同泄漏量下具有最大开启力的优化工况点,通过将这些工况点拟合从而得到优化工况曲线。多目标优化工况曲线法计算流程图如图8所示。
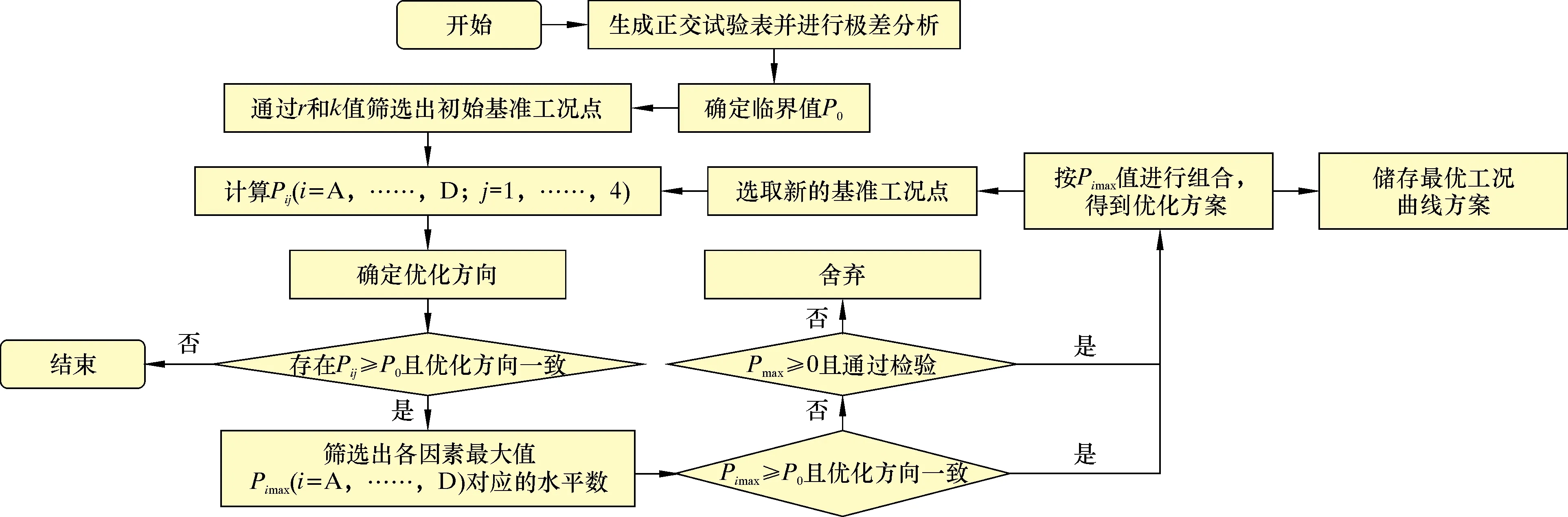
图8 多目标优化工况曲线法计算流程图
r值反映了不同因素对目标函数的贡献率,通过比较泄漏量和开启力下各因素对应的r值,将贡献率较大的r值作为目标参数,并选出其对应因素的最大k值的水平参数,可初步得到密封端面结构参数的较好组合,即A4B1C5D3E1。


图9 开启力与泄漏量之间的变化曲线
以极差分析出的A4B1C5D3为基准,计算出其他各个因素对应各水平的P值,当以开启力减小的方向作为优化方向时,其对应的P值均小于P0,无法进行优化,所以组合A4B1C5D3已经为开启力最小的优化组合,因此以开启力增大的方向作为优化方向,一级P值如表3所示。
由表3可以看出,各因素中P值最大值对应的水平参数为A1、B3、C1、D1,其值分别为579.44、13.93、61.14、107.94。其中B3、C1对应P值小于75.84,对A1B1C1D1E1和A1B3C1D1E1组合进行密封膜流场数值模拟,模拟结果具有优化效果,通过验证接受B3。为此提出了更优的组合方案:A1B1C5D3E1、A1B1C5D1E1、A1B1C1D1E1和A1B3C1D1E1。

表3 一级P值
以上4种组合具有良好的优化效果,且开启力得到了一定的提高,但开启力并未达到峰值。为了进一步提高开启力,重复上述优化方法,选择具有较高开启力的组合A1B3C1D1E1为基准,以开启力增大方向为优化方向,计算各个水平对应的P值,即二级P值。满足开启力为正值且二级P值大于P0只有A2,此外大于0且满足优化方向的有C4和D5,以此进行密封膜流场数值模拟计算,结果表明优化效果不明显。
将得到的具有较高开启力的组合A2B3C1D1E1,再以组合A2B3C1D1E1作为基准,以开启力增大方向为优化方向,计算三级P值,得到其值均低于P0,无法进行优化,所以组合A2B3C1D1E1即为最大开启力的优化组合。
以两级优化基准A4B1C5D3E1、A1B3C1D1E1及优化组合A1B1C5D3E1、A1B1C5D1E1、A1B1C1D1E1、A2B3C1D1E1汇总,得到表4所示的最优工况曲线方案,同时计算得到其泄漏量及开启力。

表4 最优工况曲线方案
将最优工况曲线方案绘成曲线,得到了基于正交试验方法的优化曲线,如图10所示。将优化工况点进行拟合,得到优化工况拟合曲线:

图10 多目标参数最优工况曲线
F=0.264Q3-11.422Q2+192.019Q-259.060
(9)
拟合优度R2=0.989,这说明拟合效果良好,基本可以反映出优化曲线趋势。
从图10可知,筛选出的6组组合均在正交试验曲线的左上侧,其中实线即为多目标参数最优工况曲线,表明选择出来的组合与25组正交试验相比,在相同的泄漏量情况下,会有更大的开启力。在低泄漏量时也有较大的开启力,在高泄漏量时具有更高的开启力峰值,且曲线一直保持着较快的增长趋势,优化效果显著。通过最优工况曲线可以对已知结构进行预测,若测得的泄漏量和开启力符合优化工况拟合曲线,则为较为优化的结构;若在该曲线的下方,则说明还有优化的空间。研究结果可为离心泵机械密封端面空化中的结构优化提供理论指导。
5 结 论
(1)在考虑离心泵机械密封端面空化下,定义了槽位系数λ,且λ对液膜空化影响显著。当槽位系数λ为0时,气相体积分数最低,约为10%。随着槽位系数λ的增大,会导致液膜中发生剧烈空化,气相体积分数陡增。当槽位系数λ在0.5附近时,气相体积分数达到峰值。当气相体积分数大于20%时,开启力基本小于200 N,会导致密封的不稳定运行。
(2)基于正交试验研究,提出了多目标最优工况曲线法,以P值(泄漏量增量ΔQ/开启力增量ΔF)为优化评价指标,得到6组开启力由最小到最大的优化工况点,且拟合曲线满足三次四项式,为螺旋槽结构的选择和优化提供了理论基础。基于最优工况曲线法可处理正交试验的多目标优化问题,具有普适性。
