水平井井眼曲率对膨胀管通过性的影响研究*

周 兰 孙巧雷 王高磊 马 越 冯 定

(长江大学机械工程学院；湖北省油气钻完井工具工程技术研究中心)

0 引 言

目前，由于常用的取换套、爆炸整形及套管补贴等修复技术已不适用于水平井多段破损或破损段较长的修复作业，所以油田现场大多采用膨胀管补贴进行修复[1-2]。膨胀管在水平井下入过程中，受井眼轨迹的影响会发生弯曲，且膨胀管螺纹连接处可能挤压受损，导致强度降低甚至发生脱扣现象[3-5]。

针对水平井的管柱下入及通过性问题，部分学者开展了相关研究工作。冯定等[6]基于结构力学和位移法，在充分考虑井筒摩阻、管柱自重及井眼轨迹等多种因素的影响下，推导出了多分层管柱整体通过性的研究方法；祝效华等[7]基于弹塑性理论，利用Abaqus非线性分析软件，研究了套管通过水平井弯曲段时的力学行为，并总结出套管通过水平井弯曲段时的下入规律；罗有刚等[8]在考虑管柱组合结构、流体摩阻及管柱存在多变径部位等影响因素下，建立了冲砂管柱下入摩阻预测模型；代理震[9]针对水平井压裂管柱封隔器的下入安全进行了预测，并推导出可通过造斜段工具最大长度的计算公式。但是，目前尚无学者针对井眼弯曲现象严重及井眼曲率大的水平井开展膨胀管的通过性影响因素研究。

为此，本文基于膨胀管在水平井中的下入过程，在考虑膨胀管所受重力、浮力、摩阻、弯矩、剪力及流体作用力等的情况下[10-12]，对膨胀管微元段进行受力分析，建立膨胀管下入载荷计算模型以及井眼曲率影响下产生的附加轴力计算模型；在考虑膨胀管螺纹不同螺纹牙中径和轴向载荷等不同情况下，建立膨胀管内、外螺纹连接强度条件。此外，运用所建立的模型分析了CA水平井井眼曲率对膨胀管通过性的影响，包括膨胀管通过性分析、井眼曲率对膨胀管通过性的影响分析以及极限曲率的计算与分析。所得结果可为大井眼曲率水平井下入膨胀管困难提供有效解决方案和理论依据。

1 膨胀管下入载荷计算模型建立

1.1 膨胀管下入受力分析

基于水平井井眼轨迹，选取膨胀管为研究对象。受力分析前，将膨胀管分为若干个微元段，在综合考虑膨胀管所受重力、轴向载荷、浮力、摩阻、弯矩、剪力和流体作用力等影响下，对膨胀管微元段进行受力分析并建立受力载荷模型[13-18]。相比于其他下入受力模型，该模型适用于井眼弯曲现象严重和井眼曲率大的水平井，且考虑了膨胀管的刚性，更符合现场实际工况。建立模型前，首先做如下假设：①膨胀管轴线与井眼轴线一致；②膨胀管与井壁连续性接触，且井壁为刚性；③膨胀管微元段受力均匀；④忽略温度效应对膨胀管的影响；⑤膨胀管微元段的曲率为常数；⑥忽略膨胀管下入过程中由于变形效应所导致的内外径变化；⑦忽略膨胀管下入时扭矩的影响。

图1 膨胀管微元段受力分析图

根据受力平衡可得膨胀管微元段各作用力的关系式：

(1)

膨胀管微元段的均布接触力为：

(2)

式中：μ为膨胀管与井壁间的摩擦因数，“±”分别表示膨胀管上提、下放两种工况；N为膨胀管微元段接触力的合力，N/m；Nn、Nb为膨胀管微元段主法线、副法线方向所受的均布接触力，N/m。

膨胀管单位长度浮重为：

(3)

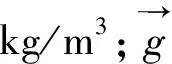
膨胀管微元段A处所受集中力为：

(4)

式中：T(s)为膨胀管微元段A处轴向力，N；Fn(s)、Fb(s)分别为膨胀管微元段A处的主法线、副法线方向所受的剪力，N。

膨胀管微元段B处所受集中力为：

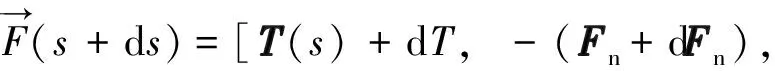
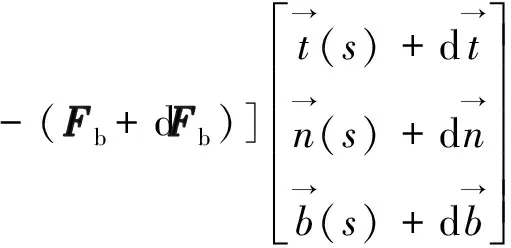
(5)

式中：dT为膨胀管微元段的轴向力增量，N；dFn、dFb分别为膨胀管微元段主、副法线上的剪力增量，N。

(6)

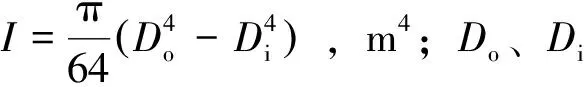
1.2 曲率附加轴力

当膨胀管下入到水平井的弯曲段时，受井眼曲率的影响其会产生附加轴力。若曲率过大，则会对膨胀管产生一定的破坏，且膨胀管螺纹连接处可能挤压受损，导致强度降低甚至脱扣。因此，基于材料力学的压杆失稳理论，建立了膨胀管的挠曲线近似微分方程，通过求解可得膨胀管曲率附加轴力的计算公式。

膨胀管挠曲线近似微分方程为：

(7)

式中：M(x)为膨胀管x处截面弯矩，N·m；Fw为膨胀管弯曲临界力，即曲率附加轴力，N；δ为膨胀管自由端挠度，m；ω为膨胀管x处的挠度，m。

对上式简化并求解，可得该微分方程通解为：

ω=Asin(kx)+Bcos(kx)+δ

(8)

式中：A、B、k为待定常数。

边界条件：x=0处，ω=0；x=l处，ω=δ。

通过对通解求导，并将边界条件代入求解，可得膨胀管曲率附加轴力：

(9)

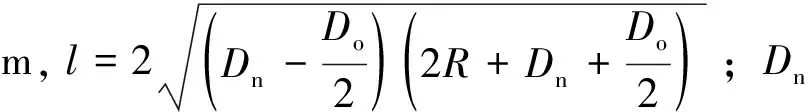
2 曲率对膨胀管通过性的影响

2.1 膨胀管内、外螺纹连接强度条件

由于膨胀管螺纹不同位置的中径、轴向载荷不同，导致螺纹牙发生破坏的危险截面具有不确定性，且由于其连接失效受到轴向载荷、螺纹结构、螺纹尺寸、螺纹各截面处复合应力及腐蚀环境等多个因素的综合影响，需结合相应位置的螺纹中径参数和轴向载荷来分别进行螺纹牙的失效条件判定[19-20]，取其最大工作应力。因此，考虑膨胀管外螺纹存在拉应力、内螺纹存在压应力以及螺纹面上的剪应力，基于第四强度理论，可分别得膨胀管内、外螺纹连接应力[21]。

膨胀管内螺纹连接应力：

(10)

膨胀管外螺纹连接应力：

(11)

式中：σni、σwi分别为膨胀管内、外螺纹连接应力，MPa；[σn]、[σw]分别为膨胀管内、外螺纹许用屈服应力，MPa；Ti-1为第i-1圈膨胀管螺纹的轴向载荷，N；Ani、Awi分别为内、外螺纹连接处的螺旋副接触面积，m2；T1、T2分别为螺旋副与接触面间的摩擦力矩，N·m；T1j为第j个螺纹牙处的摩擦力矩，N·m；Wni、Wwi分别为内、外螺纹连接处螺旋副的接触面抗扭截面系数。

2.2 极限曲率分析

基于以上分析，当膨胀管下入到弯曲段时，在曲率不同的情况下会产生不同的曲率附加轴力，从而导致膨胀管轴力发生变化，最终使膨胀管内、外螺纹连接应力变化。当曲率越大时，曲率半径则越小，膨胀管可通过的最大长度也随之减小，曲率附加轴力则越大，从而导致内、外螺纹连接应力随之增大。因此，当水平井井眼曲率增大到一定值时，膨胀管内、外螺纹连接应力可能大于螺纹连接部位的许用屈服应力，从而产生破坏导致失效。

为减轻膨胀管下入时井眼曲率的影响，需分析膨胀管下入到不同井深下的极限曲率。根据膨胀管螺纹连接处的许用屈服强度，可确定其极限连接应力，从而可分别确定膨胀管轴力、曲率附加轴力以及极限曲率，以此可计算出膨胀管下入到各井斜角处所对应的极限曲率。

3 应用实例

本文以CA水平井为例，分析水平井井眼曲率对膨胀管通过性的影响。下入膨胀管管柱组合：可捞底堵×0.50 m+膨胀管×18.00 m+ø105 mm膨胀锥×0.18 m +ø90 mm膨胀锥连接杆×0.58 m+ø73 mm工具油管。其中：膨胀前膨胀管本体外径为108 mm，内径为94 mm，长度为6 m；螺纹连接处外径为110 mm，内径为94 mm。通过计算并对比两段螺纹的轴向力及内、外螺纹连接应力，靠近井底螺纹的第二牙受力较大，因此以下分析选取靠近井底螺纹的第二牙为研究对象，以确保两段膨胀管螺纹的连接应力均符合强度要求。

基于以上参数，分析了膨胀管在CA水平井中下入的通过性、井眼曲率对膨胀管通过性的影响以及极限曲率，主要包括对膨胀管下入时的实际钩载、最小通过轴力(下入轴力+曲率附加轴力)、内外螺纹连接应力及极限曲率的分析计算，主要计算步骤及分析结果如下。

3.1 膨胀管通过性分析

为分析膨胀管在CA水平井中下入时的通过性，使用式(6)计算了膨胀管下入到不同井斜角位置时的实际钩载，并使用式(6)和式(9)计算可得下入轴力和曲率附加轴力，将二者相加，可得膨胀管下入到各井斜角位置处，曲率为每30 m井段1°～10°范围内的最小通过轴力，最终选取各组数据中最小通过轴力的最大值与相对应井斜角下入位置的实际钩载进行对比，结果如图2所示。由图2可知，膨胀管下入到各井斜角处的实际钩载均大于最小通过轴力的最大值。因此，从钩载角度来看，膨胀管可下入到CA水平井中各井斜角位置。

图2 不同井斜角处最小通过轴力的最大值与实际钩载对比曲线

3.2 井眼曲率对膨胀管通过性的影响分析

为分析水平井井眼曲率对膨胀管通过性的影响，分别计算了膨胀管下入到各井斜角α位置时，不同曲率下的最小通过轴力和内、外螺纹连接应力，计算结果如图3和图4所示。其中：使用式(6)和式(9)分别计算下入轴力和曲率附加轴力，二者之和即为最小通过轴力；通过式(6)计算不同曲率下的轴向载荷，将各轴向载荷代入式(10)和式(11)可分别得不同曲率下的内、外螺纹连接应力。

图3分析了井斜角分别为15°、35°、55°和75°处不同曲率下的最小通过轴力。由图3可以看出：最小通过轴力随曲率的增大而增大；在同一曲率下，最小通过轴力的变化与井斜角的大小并无直接相关关系。这是因为井眼曲率越大，膨胀管的可通过最大长度越短，此时膨胀管的下入则需要更大的通过轴力，而水平井井眼曲率的变化并不受井斜角变化的影响，因此井斜角的变化并不会导致最小通过轴力发生变化。

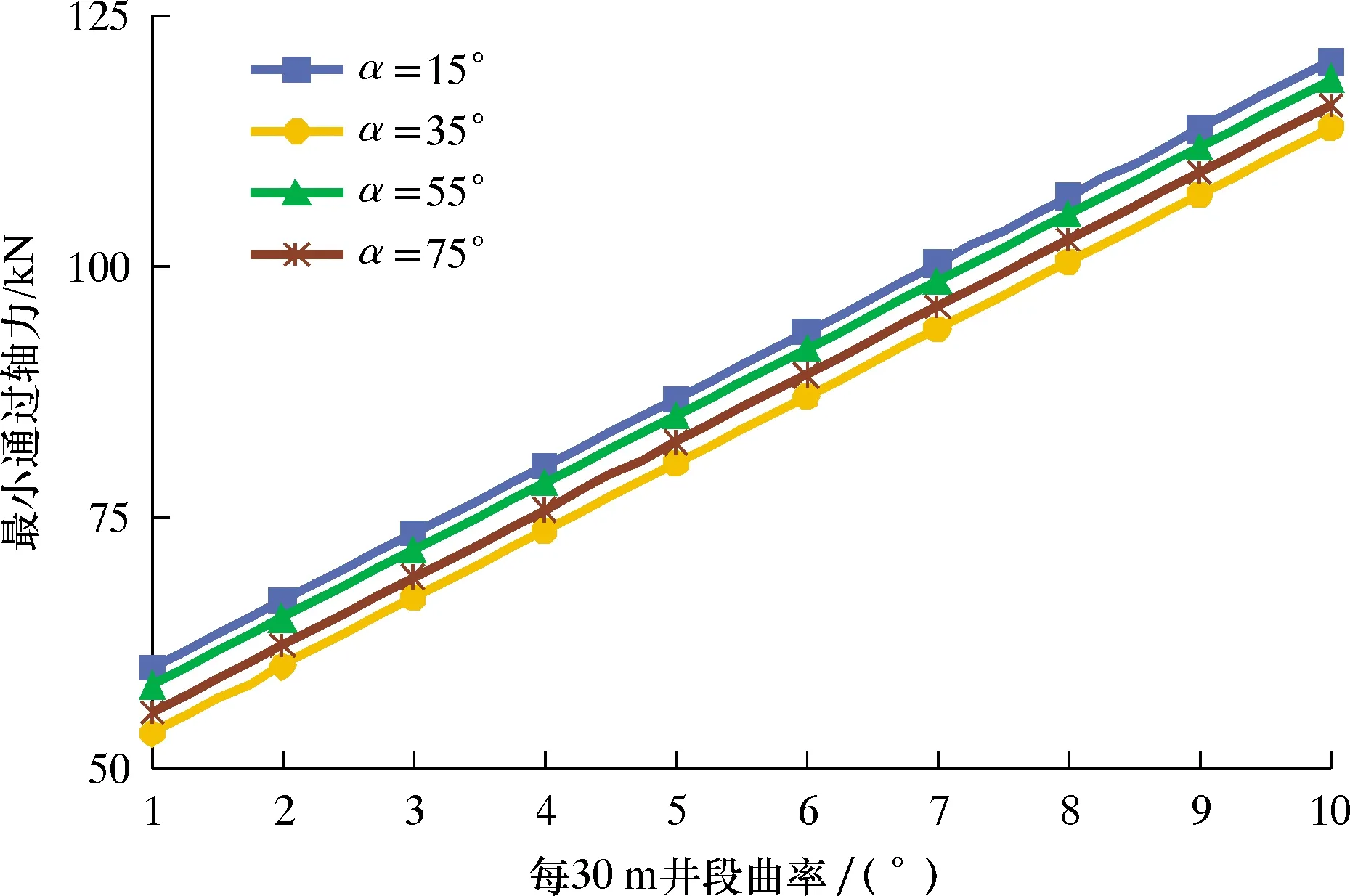
图3 不同曲率下的最小通过轴力曲线

图4分析了井斜角分别为15°、35°、55°和75°处不同曲率下的膨胀管内、外螺纹连接应力。由图4可以看出：膨胀管内、外螺纹连接应力均随曲率的增大而增大，且同一井斜角位置处相同曲率下的外螺纹连接应力均大于内螺纹连接应力；同一曲率下，内、外螺纹连接应力的大小并不随井斜角的变化而变化。这是因为曲率的增大会导致曲率附加轴力和最小通过轴力增大，从而使内、外螺纹连接应力增大。由此分析结果可知，判断膨胀管在下入过程中是否破坏应主要考虑井眼曲率的影响，与下入位置的井斜角大小并无关系。

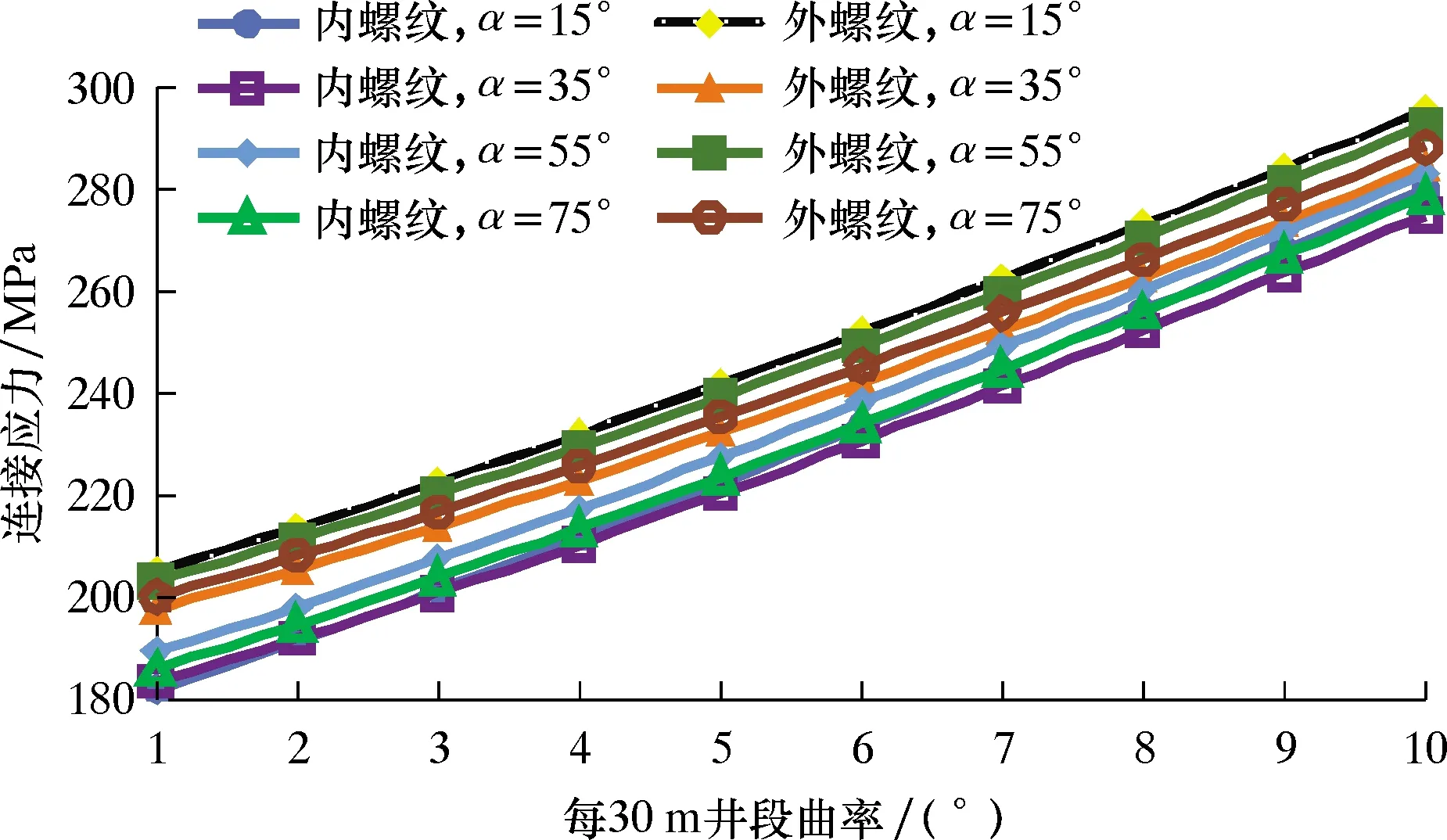
图4 不同曲率下的内、外螺纹连接应力曲线

3.3 极限曲率的计算与分析

图5展示了膨胀管下入到不同井斜角位置时的极限曲率，并与膨胀管下入至CA水平井相对应井斜角位置下的井眼曲率进行对比。其中，膨胀管屈服强度取440 MPa，安全系数取1.2，由此可得许用屈服强度，将此作为极限连接应力，从而通过式(10)、式(11)、式(6)以及式(9)可分别确定膨胀管轴力、曲率附加轴力以及极限曲率。

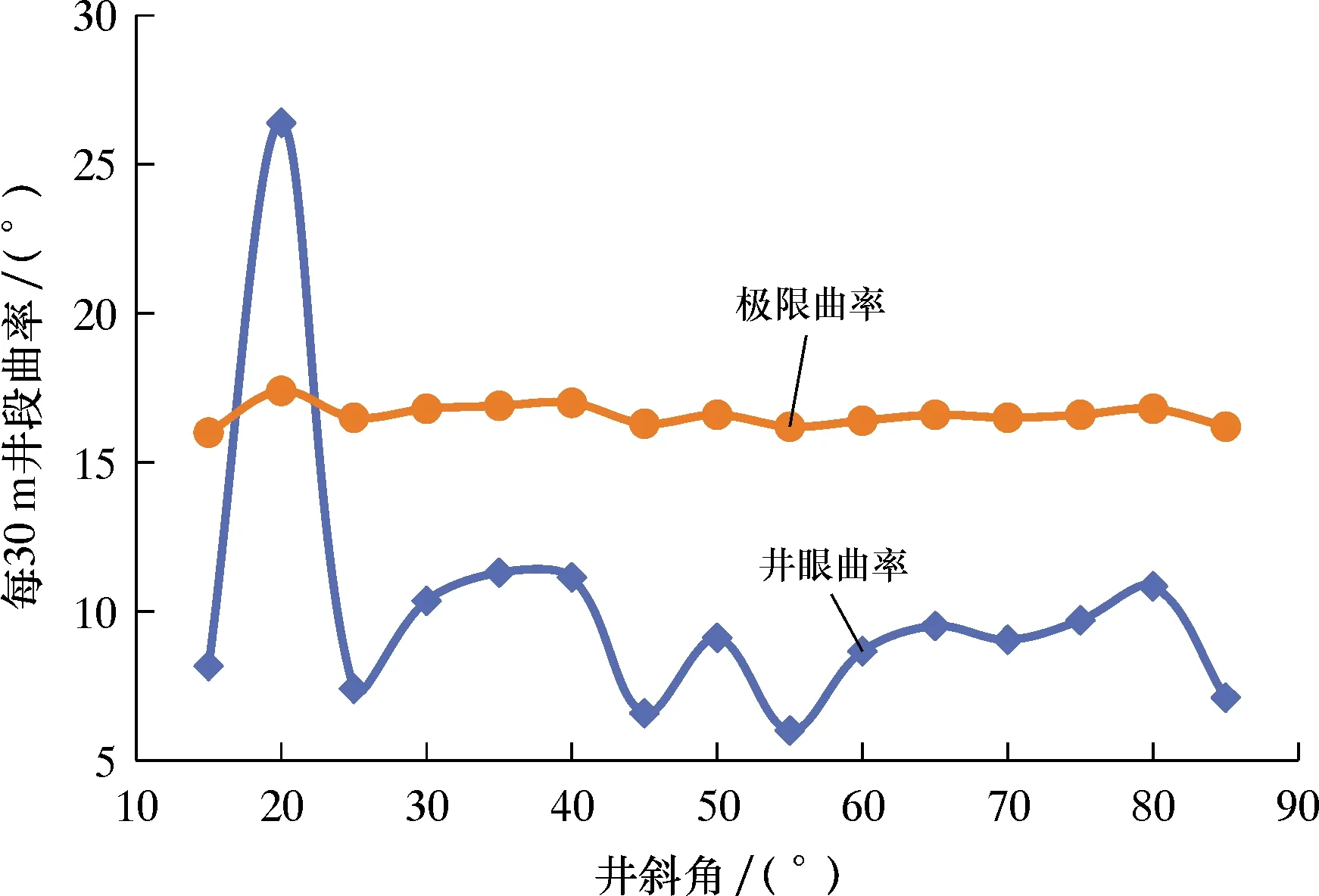
图5 不同井斜角处的井眼曲率与极限曲率的对比曲线

计算结果表明，CA水平井各井斜角位置的井眼曲率中，存在大于极限曲率的情况。因此，膨胀管在下入过程中会受到破坏，而在CA水平井的现场施工过程中，起出膨胀管的脱扣及起出膨胀锥连接杆的弯曲现象则证实了这一结论的准确性。

对结果进一步分析可知，在计算的各井斜角位置中，井斜角为20°时的极限曲率大于井眼曲率，说明膨胀管下入到此位置时，其强度不满足膨胀管材料的屈服强度，从而会导致膨胀管发生破坏。

4 结 论

(1)针对井眼弯曲现象严重及井眼曲率大的水平井，综合考虑膨胀管下入过程中所受重力、浮力、弯矩、剪力及流体作用力等的影响，建立了膨胀管在水平井中下入时的受力载荷模型，可用于计算膨胀管下入的轴力和钩载，且建立了曲率附加轴力的计算模型，膨胀管下入轴力和曲率附加轴力之和即为最小通过轴力，将最小通过轴力和钩载进行对比即可初步判断膨胀管的通过性。

(2)提出了计算极限曲率的方法，通过此方法可得水平井各位置的极限曲率，将其与井眼曲率对比可判断膨胀管在下入过程中是否会受到破坏，且可初步判断膨胀管强度破坏的下入位置。

(3)通过分析曲率对膨胀管通过性的影响，膨胀管内、外螺纹连接应力随曲率的增大而增大，且同一井斜角位置处相同曲率下的外螺纹连接应力均大于内螺纹连接应力；从钩载和最小通过轴力最大值的对比来看，膨胀管可下入至CA水平井中的各井斜角位置处，但从井眼曲率和极限曲率的对比来看，膨胀管在下入过程中会受到破坏，分析结果与CA水平井的现场施工情况相符。