矮塔斜拉桥塔墩梁固结区应力分析

周西游, 张 斌, 席晓旭, 张传兵, 彭 清

（中国中铁二局集团 第四工程有限公司, 四川 成都 610300）

0 引言

黎耀[1］等采用有限元软件, 对塔墩梁固结部位在最不利工况进行应力分析发现墩梁固结处存在一定的应力集中, 提出适当加密钢筋的方法以确保安全。刘子君[2］等选用有限元软件分析了在主梁截面在最大负弯矩状态下的墩顶的应力分布, 结果表明该区域以受压为主。曹忠强[3］建立了局部分析模型对塔墩梁固结区的三向应力进行分析。发现塔梁固结部位存在主拉应力集中现象, 建议增加配筋以抵抗拉应力。徐华锐[4］等以模型试验为背景, 提出了有效模拟塔墩梁锚固区复杂受力状态加载方法。覃耀柳[5］等通过有限元分析发现悬臂最大悬臂状态下塔梁墩固结区受力最不利, 建议该部位可采用钢纤维混凝土。彭定成[6］等的分析中发现在翼缘端部出现拉应力；墩梁固结区存在应力集中的现象。

由于塔梁墩固结区构造比较复杂, 索塔与主梁、主梁与主墩之间构件的刚度变化较大, 容易造成局部应力集中, 而这些现象在整体模型中不能得到全面反映。因此, 有必要运用有限元软件建立实体仿真分析模型, 对塔梁墩固结区进行细部分析, 探究该区域更真实、更详细的空间应力分布规律, 以优化该区域的构造和配筋设计, 保证结构设计的合理性和安全性。但较少有文献介绍局部模型加载边界条件的验证情况。本文在梳理局部模型的边界条件的基础上, 对加载边界条件简化进行验证判断, 确保边界条件准确无误, 建立局部三维分析模型, 在确定计算分析模型的基础上探究不同参数下墩塔梁固结段的真实应力状态, 为指导结构配筋、保证结构安全起到了非常重要的作用。

1 工程概况

博罗东江特大桥（90+180+90）m 矮塔斜拉桥采用双薄壁矩形截面桥墩, 截面尺寸为17.8 m×3.2 m。0#块长度11 m, 截面最大高度为9.6 m。桥塔用双柱式桥塔形式, 桥面以上塔高29.9 m。塔柱采用矩形实体截面, 顺桥向宽4.8 m, 横桥向宽2.4 m, 四周设30 cm×30 cm切角。

2 试验研究

2.1 测点布置

依据国内外已有研究, 为明确塔墩梁固结区混凝土受力规律, 确定了传感器的具体布置位置。选择塔底和桥墩顶部位置布置应力传感器, 具体布置位置个数量如图1～图3所示。

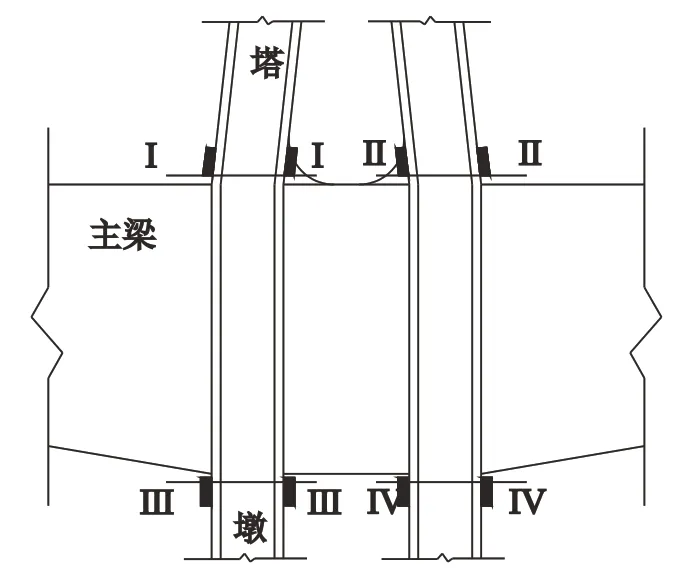
图1 塔墩梁位置布置图

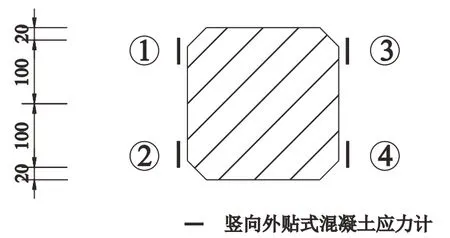
图2 墩底布置

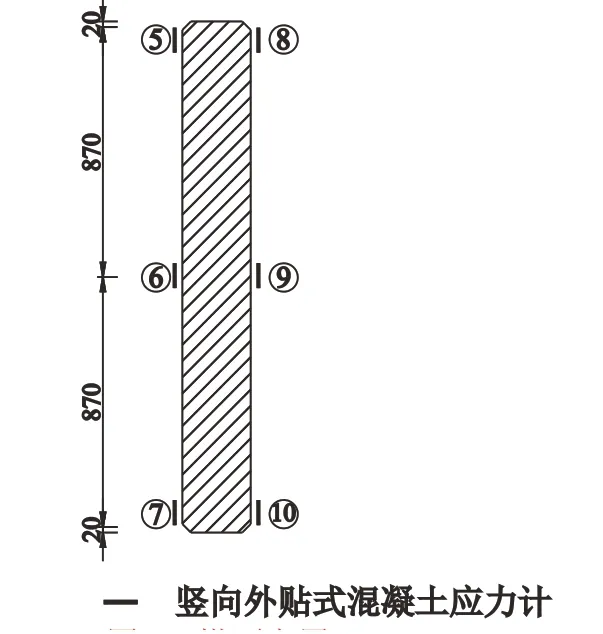
图3 塔顶布置

墩顶共布置2个断面, 每个断面共需布置6个竖向应力传感器, 共需12个应力传感器。塔底每个断面布置4 个传感器, 供需8 个应力传感器, 塔墩梁连接部位供需20个传感器。

2.2 测试结果

对施工全过程进行监测, 依据现场实测数据明确塔墩梁固结区混凝土的实际受力状态及不同施工阶段塔墩梁固结区混凝土应力的变化规律, 为此类桥梁的后续施工提供技术支撑。限于篇幅, 仅选取1#、2#、5#和8#测点数据进行分析。具体应力变化如图4～图7所示。

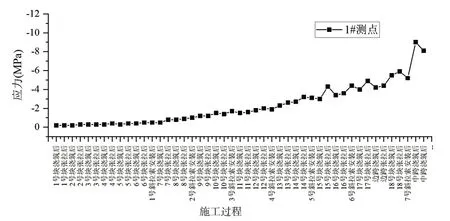
图4 不同施工阶段下1#测点的应力变化

图5 不同施工阶段下2#测点的应力变化

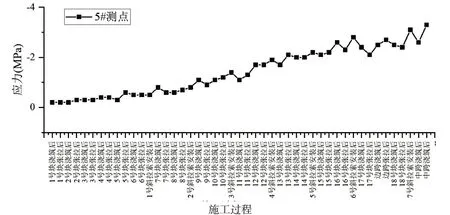
图6 不同施工阶段下5#测点的应力变化

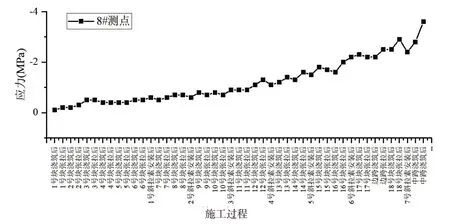
图7 不同施工阶段下8#测点的应力变化

在整个施工过程中, 塔墩梁固结区塔底位置处不同测点的应力随着施工阶段的增加应力不断增加, 且最大压应力仅为9.0 MPa, 远小于容许压应力。塔墩梁固结区墩顶位置处不同测点的应力随着施工阶段的增加应力不断增加, 且最大压应力仅为4.4 MPa, 远小于容许压应力。整个施工过程中, 塔底和墩顶均未出现拉应力。

3 有限元建模及验证

3.1 有限元分析模型

利用大型有限元分析软件, 采用由上而下的建模方法, 纵桥向为X 轴, 横桥向为Y 轴, 竖向为Z 轴, 建立塔墩梁固结部位的几何模型。该实体模型采用四面体划分, 单元类型为C3D10, 为十结点二次四面体单元。采用基于圣维南原理的子模型方法[7-8］, 整体模型为局部模型提供边界条件。本模型的边界条件为塔墩底部固结。为了避免边界条件对固结区受力的影响, 主梁、塔柱、桥墩的截取面离固结区的距离应足够长。局部分析模型采用等效荷载法来模拟预应力[9］。被截断的预应力钢束, 预应力效应已经包含在从整理模型中所提取的边界内力中, 而锚固在模型内的预应力钢束, 则需要等效成外荷载的形式作用在模型上。预应力钢束与混凝土之间产生的摩擦力当作外荷载加至模型上, 才能使得力的平衡条件得到满足。

局部模型有5个切割面, 施加在这5个面的位移和荷载称为边界条件。边界条件选择是否合适, 直接影响到固结区的应力分析结果。经过试算, 分别在主梁左端、主梁右端切面处和上端塔柱一个切面处施加内力边界条件, 在下端塔柱2个切面处施加固定约束, 以消除刚体位移, 能够较准确地模拟固结段的边界条件。为了使荷载施加方便, 在各边界截面的质心处均建立主节点, 截面上其余节点与主节点之间形成刚域, 边界条件均施加在主节点上。采用等效荷载法施加荷载。具体计算分析模型如图8所示。

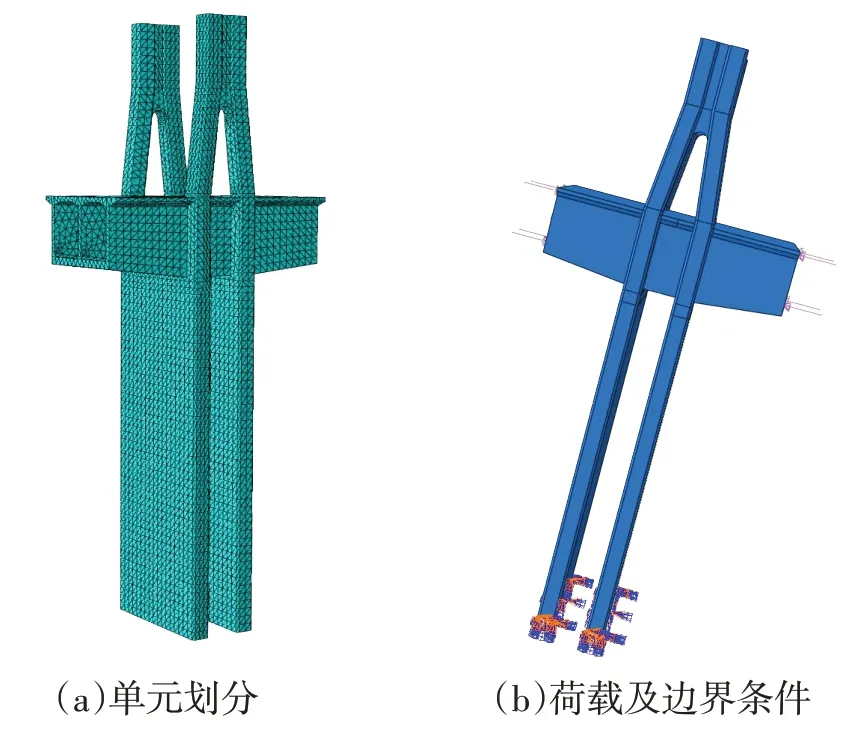
图8 塔墩梁固结局部模型

3.2 计算值与实测值对比

通过对比典型位置测点的理论值与实测值, 验证模型的合理性和准确性, 限于篇幅仅对1#测点和5#测点进行对比, 具体对比如图9和图10所示。

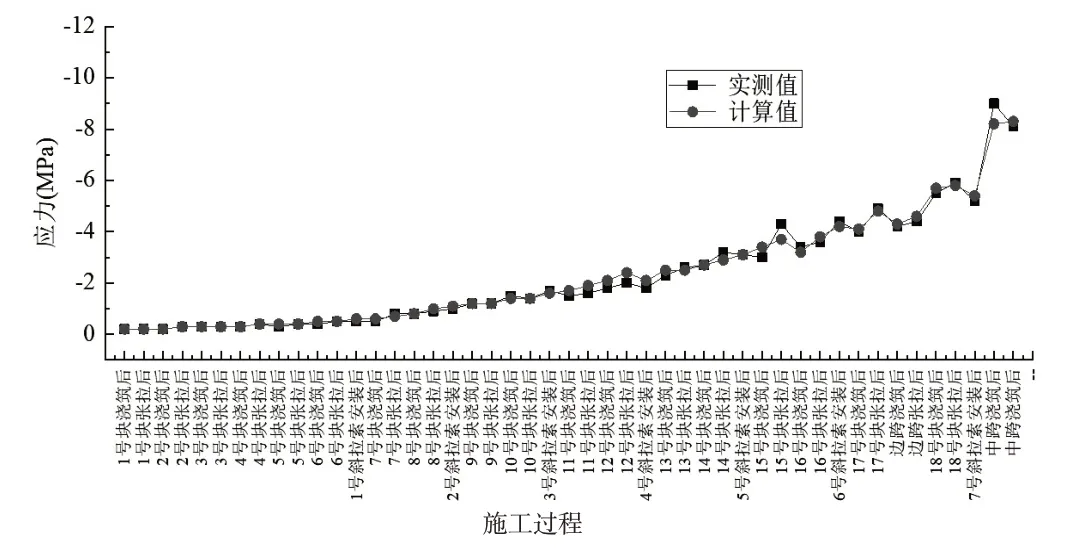
图9 不同施工阶段下1#测点的应力对比

图10 不同施工阶段下5#测点的应力对比

由图9 和图10 可知, 塔墩梁固结区不同测点在不同施工阶段的应力计算值与实测值变化规律一致。塔墩梁固结区的计算值与实测值的误差在-10.67%～9.07%, 该计算分析模型可有效模拟塔墩梁固结处在不同施工阶段的受力特征。

4 参数分析

依据上述计算分析模型对成桥后收缩徐变对塔墩梁固结区受力的影响及整体升温和梯度温度对塔墩梁固结区受力的影响。

4.1 收缩徐变

考虑混凝土的收缩徐变对塔墩梁固结区受力的影响, 考虑混凝土的收缩徐变对塔墩梁固结区受力的影响, 计算结果见表1和表2所列。

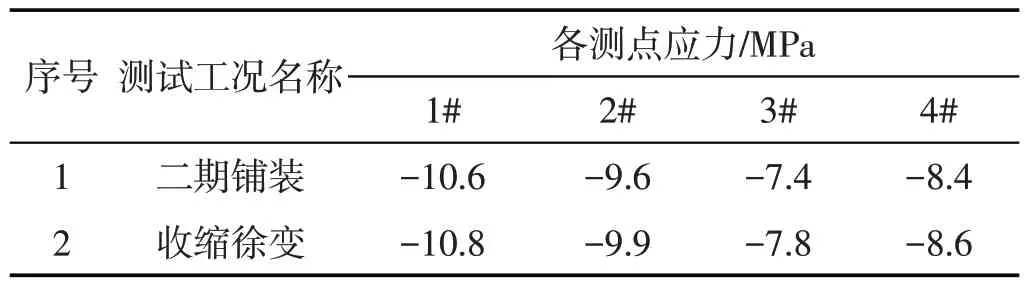
表1 塔底测点应力

由表1和2可知, 收缩徐变对混凝土压应力的影响较小, 竖向应力随着时间的变化会有所增大, 但变化幅度不大, 说明收缩徐变对塔墩梁固结区的混凝土的应力影响较小。

4.2 整体升温

四季的变化, 桥梁经历从冬季的低温到夏季的高温, 温度的变化也是桥梁受力不可忽略的一个重要的因素。采用上述计算分析模型对塔墩梁固结区进行整体升温10 ℃和20 ℃及整体降温10 ℃和20 ℃的受力分析。仅给出1#测点和5#测点在温度变化下的应力情况, 见表3和表4所列。

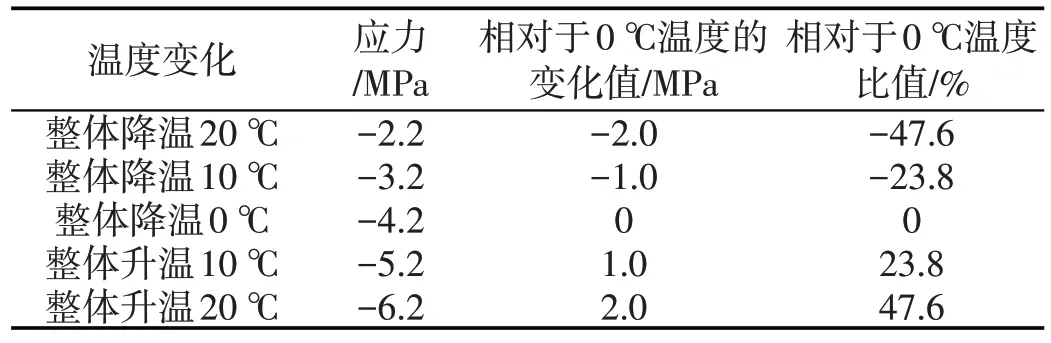
表3 整体温度变化对索梁受力的影响（1#测点）

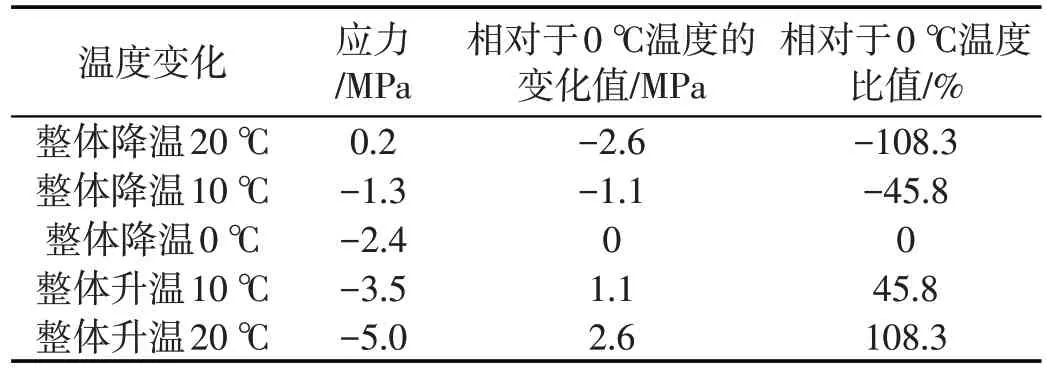
表4 整体温度变化对索梁受力的影响（5#测点）

由表3和表4可知, 整体升温和整体降温对结构受力的影响基本呈线性变化, 整体降温时塔底外侧混凝土的压应力减小, 内侧混凝土的压应力增大, 最大变化量为47.6%和61.5%；墩顶外侧混凝土压应力减小, 最大变化量达到了108.3%, 当降温达到20 ℃时, 外侧出现拉应力, 设计时需要考虑增设竖向拉筋。整体升温时塔底外侧混凝土的压应力会增大, 内侧混凝土压应力减小, 墩顶混凝土外侧压应力增大。

4.3 梯度温度

塔墩梁固结区在太阳照射的一面和未照射的一面会出现温度差, 两侧的温度不同也会对其受力产生影响, 因此梯度温度也是桥梁受力不可忽略的一个重要的因素。采用上述计算分析模型对塔墩梁固结区进行温差10 ℃和温差20 ℃的三向应力进行受力分析, 仅给出1#测点和5#测点在梯度温度下的应力情况, 见表5所列。

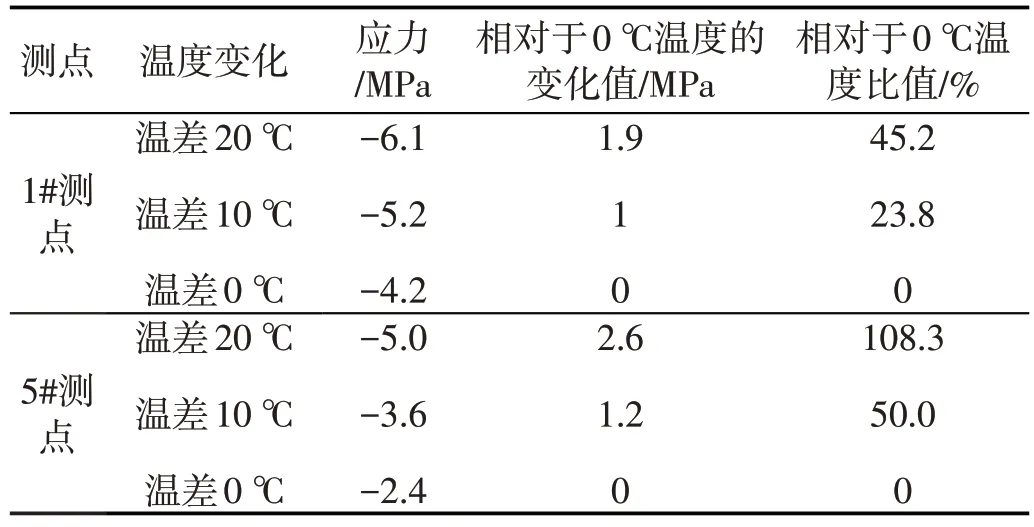
表5 梯度温度变化对索梁受力的影响

从表5中可以看出, 梯度温度对塔底和墩顶混凝土应力有一定的影响, 当温差达到20 ℃时, 相对于温差为0 ℃时塔底混凝土应力变化最大为45.2%, 相对于温差为0 ℃时墩顶混凝土应力变化最大为108.3%, 温度梯度对墩顶混凝土应力的影响较大, 设计时应考虑墩顶混凝土压应力的富余量, 以免因温差过大而使墩顶混凝土压碎。

5 结论

（1）在整个施工过程中, 塔墩梁固结区塔底位置和墩顶位置处不同测点的应力随着施工阶段的增加应力不断增加, 且最大压应力远小于容许压应力。整个施工过程中, 均未出现拉应力。

（2）实测数据和理论计算的对比分析结果验证了该计算分析模型的正确性和合理性, 为精确计算塔墩梁固结区混凝土的受力提供了技术支撑。

（3）收缩徐变对混凝土压应力的影响较小, 竖向应力随着时间的变化会有所增大, 但变化幅度不大。

（4）整体升温和整体降温对结构受力的影响基本呈线性变化, 整体降温时塔底外侧混凝土的压应力减小, 内侧混凝土的压应力增大；墩顶外侧混凝土压应力减小, 当降温达到20 ℃时, 外侧出现拉应力, 设计时需要考虑增设竖向拉筋。整体升温时塔底外侧混凝土的压应力会增大, 内侧混凝土压应力减小, 墩顶混凝土外侧压应力增大。

（5）温度梯度对墩顶混凝土应力的影响较大, 设计时应考虑墩顶混凝土压应力的富余量, 以免因温差过大而使墩顶混凝土压碎。