图的全-Domination染色

王彩云

(青海师范大学 数学与统计学院，西宁 810008)

1 引言与预备知识

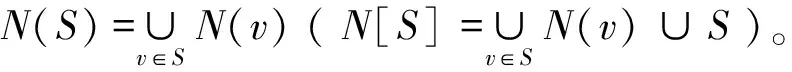
图G的一个正常点染色是一个映射f:V(G)→{1,…,k},使得图G中的任意两个相邻顶点u,v均有f(u)≠f(v)。图G的正常点染色所需要的最小颜色数称为色数,记为χ(G)。事实上,图G的正常点染色可将图G的顶点集划分为k个独立集{V1,V2,…,Vk},这里每个独立集称为一个色类,记为Vi={v∈V(G)|f(v)=i},i=1,…,k。图G的一个l-染色是指用l种颜色对G进行的一个正常点染色。

图的染色被大量用在涉及稀缺资源分配的实际问题的模型中(例如：课程表问题)，并且它在图论、离散数学和组合优化的发展中发挥了关键作用。随着应用背景的不断拓宽,一些其他染色概念被提出来。

Gera[11]等人提出了图的domiator染色的概念。图的domiator染色是指图G中每个顶点都至少与一个色类(可能是自己的色类)里的全部顶点相邻。图G的dominator染色所需的最少颜色数称为G的dominator色数,记为χd(G)。在2012年,K.Kavitha[12]研究了星和双星图族的 Middle图、Total图和Central图的dominator色数,同时还证明了上述图族的dominator色数和星色数之间的关系。

周[15]等人在dominator染色概念的基础上提出了domination染色的概念。图G的domination染色是指G的每个顶点至少与一个色类里的全部顶点相邻并且图G的每个色类的顶点要与G中至少一个顶点相邻。图G的domination染色所需的最少颜色数称为G的domination色数,记为χdd(G)。

K.P.chithra[16]等人在dominaton染色概念的基础上提出了全-do mination染色的概念。图G的全-domination染色是指G的每个顶点至少与一个色类(除了v)里的全部顶点相邻并且图G的每个色类的顶点要与G中至少一个顶点相邻。图G的全-domination染色所需的最少颜色数目称为G的全-domination色数,记为χtd(G)。图G的一个k-全-domination染色是指用k种颜色对G进行一个全-domination染色。K.P.chithra在文献[16]中研究了路、圈、路的补图和圈的补图的全-domination色数并且得出树的全-domination色数的上下界,同时刻画了树的全-domination染色数上下界相等时的充要条件。在2019年,周和赵[15]证明了对于任意图G,χdd(G)=k(k∈N*)是NP-完全的。

本文证明了对于任意图G,χtd(G)=k(k∈N*)是NP-完全的,并研究了χtd(G)和χtd(G′)之间的关系,这里G′是G通过某种操作得到的图。

2 全-domination色数的NP-完全性

定理2.1当k≥4时,任意一个图G的k-全-domination色数是NP-完全的。

证明下面给出,图G的一个k-全-domination染色与图G′的一个(k+1)-染色是等价的。

事实上,设G=(V(G),E(G))是一个没有孤立点的图,图G′是将图G添加一个新的顶点x并且使得顶点x和图G中的每个顶点都相连得到的图。下面证明χ(G)=k⟺χtd(G′)=k+1。

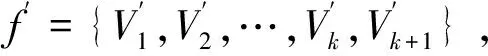
(1)f′是正常点染色。

(2)图G′中除了顶点x以外的每个顶点都可以控制颜色类Vk+1′,并且顶点x可以控制f的全部色类。

(3)图G′中除了Vk+1′以外的每一个色类都是由顶点x控制,并且Vk+1′由图G的任意一个顶点控制。

由上可知,当k≥4时,k-全-domination染色问题是NP-完全的。

3 图G-v和G-e的全-domination色数

下面研究从图G中删除一个顶点或一条边之后图的全-domination色数。

设v∈V(G),图G-v是从图G中删除顶点v得到的图。

定理3.1设G是连通图,v∈V(G)且不是割点,则χtd(G)-2≤χtd(G-v)≤χtd(G)+deg(v)-1。

证明设u,v∈V(G)且uv∈E(G),f:V(G)→{1,…,k}是图G-v的一个全-domination染色。下面对图G进行正常染色:用两种颜色m,n(m≠n∉{1,…,k})分别对顶点u和v进行染色,图G中其余顶点的染色方式是f在G-v上的限制。根据全-domination染色的定义,这种染色是图G的一个全-domination染色。因此,χtd(G)-2≤χtd(G-v)。

接下来证明χtd(G-v)≤χtd(G)+deg(v)-1。设f:V(G)→{1,…,k}是图G的一个全-domination染色,且f(v)=i。下面对图G-v进行染色:

情形1图G中仅有顶点v染i色。

用deg(v)种颜色i和cj(j=1,…,deg(v)-1,cj∉{1,…,k})对顶点v的开邻域进行染色,图G-v中其余顶点的染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图G-v的一个全-domination染色,因此χtd(G-v)≤χtd(G)+deg(v)-1。

情形2图G中除了顶点v,还有其他顶点染i色。

图G-v的顶点的染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图G-v的一个全-domination染色,有χtd(G-v)≤χtd(G)。

通过情形1和情形2,因此,χtd(G-v)≤χtd(G)+deg(v)-1。

根据定理3.1,可以得到下面的推论:

推论3.2设G是连通图,v∈V(G)且不是割点,那么|χtd(G)-χtd(G-v)可以任意大。

设e=uv∈E(G),图G-e是从图G中删除边e得到的图。

定理3.3设G是连通图,若e=uv∈E(G)且不是割边,则χtd(G)-1≤χtd(G-e)≤χtd(G)+2。

证明首先证明χtd(G)-1≤χtd(G-e)。设f:V(G)→{1,…,k}是图G-e的一个全-domination染色,下面对图G进行染色:

情形1若f(v)=f(u)=i(i∈{1,…,k})。

用颜色j(j∉{1,…,k})对顶点u或v进行染色,图G中其余顶点的染色方式是f在G-e上的限制。根据全-domination染色的定义,这种染色是图G的一个全-domination染色,因此有χtd(G)-1≤χtd(G-e)。

情形2若f(v)=i,f(u)=j(i≠j∈{1,…,k})。

图G中顶点的染色方式是f在G-e上的限制。根据全-domination染色的定义,这种染色是图G的一个全-domination染色,所以χtd(G)≤χtd(G-e)。

通过情形1和情形2,有χtd(G)-1≤χtd(G-e)。

接着证明χtd(G-e)≤χtd(G)+2。设f:V(G)→{1,…,k}是图G的一个全-domination染色,f(u)=i和f(v)=j(i≠j∈{1,…,k})。下面对图G-e进行染色：

情形1顶点v控制色类Vi且顶点u控制色类Vj。

用两种颜色m,n(m≠n∉{1,…,k})分别对点u的邻点s和点v的邻点w进行染色,并且图G-e中其余顶点的染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图G-e的一个全-domination染色,因此χtd(G-e)≤χtd(G)+2。

情形2顶点v控制色类Vi且顶点u不控制色类Vj。

用颜色m(m∉{1,…,k})对顶点u的邻点w进行染色,并且图G-e中其余顶点的染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图G-e的一个全-domination染色,因此χtd(G-e)≤χtd(G)+1。

情形3顶点v不控制色类Vi且顶点u控制色类Vj,与情况(2)的证明过程类似。

综上所述,χtd(G-e)≤χtd(G)+2。

上述两个定理分别得出了对图G删除一个点或一条边的简单操作后的图的全-domination色数,下面研究对图G进行收缩顶点集(边)和圈扩展后的图的全-domination色数。

4 图Gv，G{u,v},Ge，G⊙v和W+(G)的全-domination色数

设v∈V(G),图Gv是从G中删除顶点v使得顶点v的邻点两两连接形成的图。设S={u,v}⊆V(G)，图GS是从G中删除顶点v和顶点u后加入一个新的顶点x并且顶点x与顶点v和顶点u的邻点均相邻形成的图。图GS有两种情形:(1)顶点u和v是相邻的,不妨假设e=uv∈E(G),记为图Ge。(2)顶点u和v是不相邻的,记为G{u,v}。图G⊙v是图G删除顶点v的邻域中顶点对之间的边而得到的图,注意顶点v并没有从图G中移除。对于含圈的连通图G,C是G中的一个长度为l(≥3)的圈。图W+(G)是从图G中添加一个新的顶点x并且在顶点x与圈C上的每个顶点之间加入一条新边得到的图。上述图,参看图4-1：

图1 图例

定理4.1设G是连通图且v∈V(G),则χtd(G)-2≤χtd(Gv)≤χtd(G)+deg(v)。

证明首先证明χtd(Gv)≤χtd(G)+deg(v)。设f:V(G)→{1,…,k}是图G的一个全-domination染色。下面对图Gv进行染色,用deg(v)种颜色cj(cj∉{1,…,k})(j=1,…,deg(v))对顶点v的开邻域进行染色,并且图Gv中其余顶点的染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图Gv的一个全-domination染色,因此χtd(Gv)≤χtd(G)+deg(v)。

下面证明χtd(G)-2≤χtd(Gv)。设f:V(G)→{1,…,k}是图Gv的一个全-domination染色。对图G进行染色,用两种颜色m,n(m≠n∉{1,…,k})分别给顶点v和其邻点u染色,并且图G中其余顶点的染色方式是f在Gv上的限制。根据全-domination染色的定义,这种染色是图G的一个全-domination染色,因此χtd(G)-2≤χtd(Gv)。

根据定理3.1和定理4.1,可以得到下面的推论:

推论4.2设G是连通图,v∈V(G)且不是割点。则

定理4.3设G是连通图,则χtd(G)-2≤χtd(G{u,v})≤χtd(G)+4。

证明证明χtd(G)-2≤χtd(G{u,v})。设f:V(G)→{1,…,k}是图G一个全-domination染色,下面对图G{u,v}进行染色:用两种颜色m,n(m≠n∉{1,…,k})分别对顶点x和其邻点w进行染色,图G{u,v}中其余顶点的染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图G{u,v}的一个全-domination染色,因此,χtd(G)-2≤χtd(G{u,v})。

接下来证明χtd(G{u,v})≤χtd(G)+4。 设f:V(G)→{1,…,k}是图G{u,v}的一个全-domination染色,下面对图G进行染色:

情形1图G{u,v}中仅有顶点x染i色。

顶点u染i色并用三种颜色m,n,l(m≠n≠l∉{1,…,k})对顶点v、顶点u和顶点v的一个邻点w进行染色。图G中其余顶点的染色方式是f在G{u,v}上的限制,根据全-domination染色的定义,这种染色是图G的一个全-domination染色。因此,χtd(G{u,v})≤χtd(G)+3。

情形2图G{u,v}除了顶点x以外,还有其他顶点染i色。

用四种颜色m≠n≠l≠q(m,n,l,q∉{1,…,k})对顶点u及其一个邻点和顶点v及其一个邻点进行染色。图G中其余顶点的染色方式是f在G{u,v}上的限制,根据全-domination染色的定义,这种染色是图G的一个全-domination染色。因此,χtd(G{u,v})≤χtd(G)+4。

接下来考虑顶点u和v在G中是相邻的,即e=uv∈E(G)的情形。

定理4.4设G是连通图且e=uv∈E(G),则χtd(G)-2≤χtd(Ge)≤χtd(G)+1。

证明首先证明χtd(Ge)≤χtd(G)+1。设f:V(G)→{1,…,k}是图G的一个全-domination染色,使得f(u)=i和f(v)=j。下面给图Ge进行染色:

情形1若顶点u和顶点v都是单色类并且顶点u控制色类Vj和顶点v控制色类Vi。

顶点x染i色并且点x的一个邻点s染j色,图Ge中其余顶点的染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图Ge的全-dom ination染色,有χtd(Ge)≤χtd(G)。

情形2若顶点u不是单色类,顶点v是单色类并且顶点u控制色类Vj。

顶点x染j色并用颜色m(m∉{1,…,k})对点x的一个邻点s进行染色,图Ge中其余顶点的染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图Ge的全-domination染色,有χtd(Ge)≤χtd(G)+1。

情形3若顶点v不是单色类,顶点u是单色类并且顶点v控制色类Vi。证明过程与情况(2)的类似。

根据情形1、2和3,有χtd(Ge)≤χtd(G)+1。

现在证明χtd(G)-2≤χtd(Ge)。设f:V(G)→{1,…,k}是图Ge的任意一个全-domination染色。用两种颜色m,n(m≠n∉{1,…,k})对顶点u和顶点v进行染色并且图G中其余顶点的染色方式是f在Ge上的限制。根据全-domination染色的定义,这种染色是图G的一个全-domination染色,因此χtd(G)-2≤χtd(Ge)。

根据定理3.3和定理4.4,可以得到下面的推论:

推论4.5设G是连通图且e∈E(G)不是割边。那么

定理4.6设G是连通图且v∈V(G),则χtd(G)-deg(v)-1≤χtd(G⊙v)≤χtd(G)+1。

证明首先证明χtd(G⊙v)≤χtd(G)+1。设f:V(G)→{1,…,k}是图G的一个全-domination染色,且f(v)=i,下面给图G⊙v进行染色:

情形1图G中除了顶点v以外,还有其他顶点染i色。

用颜色m(m∉{1,…,k})对染i色的顶点(除了v)进行染色,图G⊙v中其余顶点的染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图G⊙v的一个全-domination染色,因此χtd(G⊙v)≤χtd(G)+1。

情形2图G中仅有顶点v染i色。

图G⊙v的顶点染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图G⊙v的一个全-domination染色,因此χtd(G⊙v)≤χtd(G)。

因此,χtd(G⊙v)≤χtd(G)+1。

现在证明χtd(G)-deg(v)-1≤χtd(G⊙v)。设f:V(G)→{1,…,k}是图G⊙v的一个全-domination染色,下面给图G进行染色。用deg(v)+1种颜色cj(cj∉{1,…,k}),(j=1,…,deg(v)+1)对顶点v的闭邻域染色,根据全-domination染色的定义,这种染色是图G的全-domination染色。所以χtd(G)-deg(v)-1≤χtd(G⊙v)。

根据定理4.6,可以得出下面的推论:

推论4.7设G是连通图且v∈V(G),则|χtd(G)-χtd(G⊙v)|可以任意大。

定理4.8设G是连通图,Cl是G中的长度为l的圈,则χtd(G)-l+1≤χtd(W+(G))≤χtd(G)+1。

证明首先证明χtd(W+(G))≤χtd(G)+1。设f:V(G)→{1,…,k}是图G的全-domination染色,下面对图W+(G)进行染色。用颜色m(m∉{1,…,k})对顶点x染色,图W+(G)中其余顶点的染色方式是f在G上的限制。根据全-domination染色的定义,这种染色是图W+(G)的全-domination染色,因此χtd(W+(G))≤χtd(G)+1。

现在证明χtd(G)-l+1≤χtd(W+(G))。设f:V(G)→{1,…,k}是W+(G)的一个全-domination染色。下面给图G的顶点进行染色:

情形1图W+(G)中仅有顶点x染i色。

因为图W+(G)中仅有顶点x染i色,用颜色i和l-1种颜色m(m∉{1,…,k})(m=1,…,l-1)对圈Cl上的l个顶点进行染色,图G中其余顶点的染色方式是f在W+(G)上的限制。根据全-domination染色的定义,这种染色是图G的一个全-domination染色。因此,χtd(G)-l+1≤χtd(W+(G))。

情形2图W+(G)中除了顶点x以外,还有其他顶点染i色。

用Vi表示所有染i色的顶点集合,下面给图G进行染色。用l种颜色cj(cj∉{1,…,k})(j=1,…,l)对圈C上的顶点进行染色。图G中其余顶点的染色方式是f在W+(G)上的限制。根据全-domination染色的定义,这种染色是图G的一个全-domination染色。

因此,χtd(G)-l≤χtd(W+(G))。