关于近拟常曲率空间中2-调和子流形

叶 闻， 宋卫东,2， 耿 杰

(1.安徽信息工程学院，安徽 芜湖 241000；2.安徽师范大学 数学与统计学院，安徽 芜湖 241000)

引言

以n+p表示其黎曼曲率张量取为如下形式

KABCD=a(gACgBD-gADgBC)+b(gACfBD+gBDfAC-gADfBC-gBCfAD)，

∑gACgBDfABfCD=1，

(1)

的n+p维单连通完备的黎曼流形，称为近拟常曲率空间[1].其中g是n+p的黎量度量，a,b是Nn+p的C∞—函数，{fAB}是Nn+p的一个单位向量函数。

显然，1)当a=1,b=0时，近拟常曲率空间就是单位球面Sn+p(1)。

2)当fAB可分解为λA·λB，即fAB=λA·λB时，近拟常曲率空间就是拟常曲率空间[2]，此时，其黎曼曲率张量具有如下形式

KABCD=a(gACgBD-gADgBC)+b(gACλBλD+gBDλAλC-gADλBλC-gBCλAλD)，

∑gACgBDλAλB=1，

(2)

同时文献[1]还给出了非拟常的近拟常曲率空间的例子。

在[2]中，Z.B.Bai建立了拟常曲率空间中的J.Simons型积分不等式。

定理A设Mn是拟常曲率空间中的紧致极小子流形，则下列不等式成立

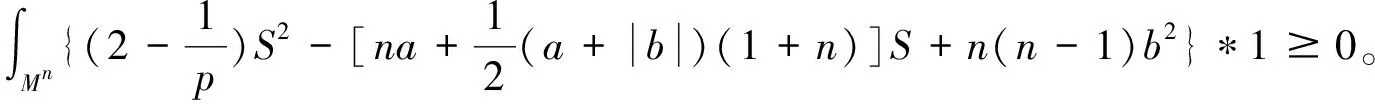
现在设f：Mn→Nn+p是等距浸入，若f是2-调和映射[3]，则称Mn是Nn+p中的2-调和子流形。姜国英[3]给出了2-调和映射所满足的条件，根据这个条件，极小子流形一定是2-调和子流形，同时，文献[3]还给出了非极小的2-调和等距浸入的实例。

本文考虑的第一个问题，在什么条件下，近拟常曲率空间中2-调和子流形是极小子流形，证明了

定理1设Mn是近拟常曲率空间Nn+p中具有平行平均曲率的n维2-调和子流形，如果第二基本形式模长‖B‖满足条件

则Mn必是Nn+p中的极小子流形。

本文考虑的第二个问题是建立近拟常曲率空间中2-调和子流形关于第二基本形式模长‖B‖的广义J.Simons型积分不等式，证明

定理2设Mn是近拟常曲率空间Nn+p中紧致无边的2-调和子流形，则成立如下的积分不等式

(3)

注：当a=1，b=0时，(3)就是常曲率空间中著名的J.Simons积分不等式。

1 预备知识

本文对各类指标的取值范围约定如下

1≤A,B,C,…≤n+p;1≤i,j,k…≤n;

n+1≤α,β,γ,…≤n+p。

设Nn+p是n+p维单连通的黎曼流形，Mn是Nn+p中n维子流形，在Nn+p上选取局部标准正交标架场{eA}，使得它们限制在Mn上，{ei}与Mn相切，设{ωA}是Nn+p关于{eA}的对偶标架场，{ωAB}是Nn+p的联络形式，则限制在Mn上，有[4]

(4)

(5)

(6)

(7)

式中B、ξ、Rijkl、Rαβkl分别是Mn的第二基本形式、平均曲率向量场、曲率张量场、法曲率张量场，KABCD是Nn+p的曲率张量场。

若Nn+p是近拟常曲率空间，则

(8)

(9)

(10)

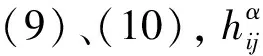
(11)

以下总假设Mn是Nn+p的2-调和子流形，则[3]

引理1Mn是Nn+p中2-调和子流形的条件是

(12)

2 定理的证明

(13)

由Cauchy不等式

(14)

又Nn+p是近拟常曲率空间。由(8)

Kαkβk=aδαβ+b(δαβfkk+fαβ)

(15)

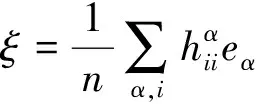
(16)

从而由(8)、(16)

(17)

又|fn+p n+p|≤1及Cauchy不等式

(18)

从而由(17)

(19)

由(13)、(14)、(19)

(20)

于是，若

(21)

则由(20)唯一的可能是

n2H2=0，

即Mn是Nn+p极小子流形。

定理2的证明由(9)

代入(12)第一式，得

两端关于指标i求共变导数，并关于i求和，得

调整指标，结合(12)第二式得

(22)

由(8)，易知Kαβkj=0。

现在计算Mn的第二基本形式模长平方的Laplacian，结合(11)、(22)，仿文献[4]

(23)

现在估计(22)式中出现的一些项，首先易见

由于Mn是紧致无边，由Stokes定理，对上面两边积分，得

(24)

由于Nn+p是近拟常曲率空间，再由(8)、(9)得

(25)

(26)

(27)

结合(8)、(16)、(18)，有

(28)

由文献[5]，有

(29)

而

(30)

由文献[4]

(31)

≥n(a-2|b|)(‖B‖2-nH2)。

(32)

由(22)-(32)及Mn的紧致，应用Stokes定理经整理，即完成定理2的证明。