隧道内燃料电池机车氢气泄漏扩散特性分析*
2022-03-21薛龙昌默帆宋立业邓佳佳刘斌
薛龙昌 默帆 宋立业 邓佳佳 刘斌
(1.中车工业研究院有限公司 北京 100160; 2.河北石家庄铁道大学机械工程学院 石家庄 050043; 3.浙江海洋大学船舶与海运学院 浙江舟山 316022)
0 引言
氢气(H2)被称为21世纪的“终极能源”,是实现碳中和的重要手段[1]。H2可通过燃料电池化学反应直接转换成电能,用于发电及交通运输等[2]。氢燃料电池动力系统应用于轨道车辆,替代传统内燃机或弓网受流系统,能显著降低建设投资,并具有高效率、无污染、低噪音等优势。目前,氢燃料电池机车主要采用若干高压氢罐储存H2,其高压罐故障时可能会导致H2泄漏。H2密度较小且易燃易爆,特别在隧道等封闭或半封闭不利于气体扩散的空间内,泄漏的H2和空气混合可能会形成氢爆炸云团,造成严重后果,因此氢燃料电池机车和其他应用中储氢系统的安全性问题亟需解决[3]。
目前,一些学者已经开展了一些关于隧道中的H2泄漏的研究,但没有足够完善的指导方针解决隧道内的安全风险。目前主要采用实验和数值模拟2种方法。在实验方面,考虑到安全问题,一些学者利用相似替代物,如氦气(He)、氮气(N2)等进行实验,这是因为H2和这些替代物泄漏扩散的规律相似,但这些气体化学性质稳定,不存在燃烧爆炸可能性[4]。另外少数学者在确保安全情况下进行H2泄漏燃烧实验。GU X等[5]通过实验研究了不同条件下隧道内H2射流的火灾特性,分析了射流火灾时对隧道内H2温度和扩散的影响,结果表明隧道内的升温速率与H2扩散速率的关系。MIDDHA P等[6]针对不同的隧道布局和一系列纵向通风条件,通过实验研究了隧道中氢燃料车辆的爆炸风险,该研究表明当隧道内纵向通风不足时,H2泄漏危险性高,可能会导致爆炸。在数值模拟方面,TOLIAS I C等[7]通过ADREA-HF计算流体动力学代码针对隧道模型中的H2爆燃评估,以无车辆隧道和有车辆隧道内的情况进行对比,结果表明考虑车辆时H2泄漏危险更大。QIAN J Y等[8]研究H2在不同泄漏位置和不同风效应下的泄漏扩散,考虑泄漏口和障碍物位置的影响,结果表明两者之间空间越窄,障碍物周围的H2浓度越大,风险因此更大。尽管已有一些学者从多个方面进行H2泄漏和扩散问题的探讨,出于安全角度,还未考虑机车储氢罐中H2在隧道内的泄漏特征等问题。
本文采用商用计算流体力学(CFD)软件对有轨电车储氢罐中H2在隧道内意外泄漏过程进行了数值模拟。首先建立真实的隧道模型,模拟了储氢罐中H2的泄漏和扩散行为分析模型,研究了H2从储氢罐的上方和下方泄漏2种工况。其次,考虑泄漏面积、隧道容积、纵向通风等不同的因素,综合分析扩散后在隧道内的分布情况。研究结果对促进氢燃料机车的应用具有积极意义。
1 CFD模型
计算域由选定的事故场景决定,包括隧道和机车的几何形状。只有1辆机车经过隧道,此处考虑沿隧道的纵向通风[9]。
1.1 几何模型
图1展示了单节列车在隧道中行驶时发生泄漏的物理模型,其中浅蓝色区域为隧道,隧道总长度为100 m,横截面宽为9.6 m,高为6.6 m;长方体为模拟机车。根据中车公司研制的燃料电池机车主要技术参数规定列车尺寸,机车总长度为30 m、宽2.65 m、高3.58 m。燃料罐距列车车头3 m,罐长为4 m。在泄漏时间和风速等参数一致的前提下,研究燃料罐上、下泄漏口发生H2泄漏的两种工况。如图1,泄漏口距离车头5 m,于罐的中心位置。上泄漏口释放的H2相对于下方更容易扩散,因为下方释放的H2会积聚在列车底部,对人员安全更具危险性。
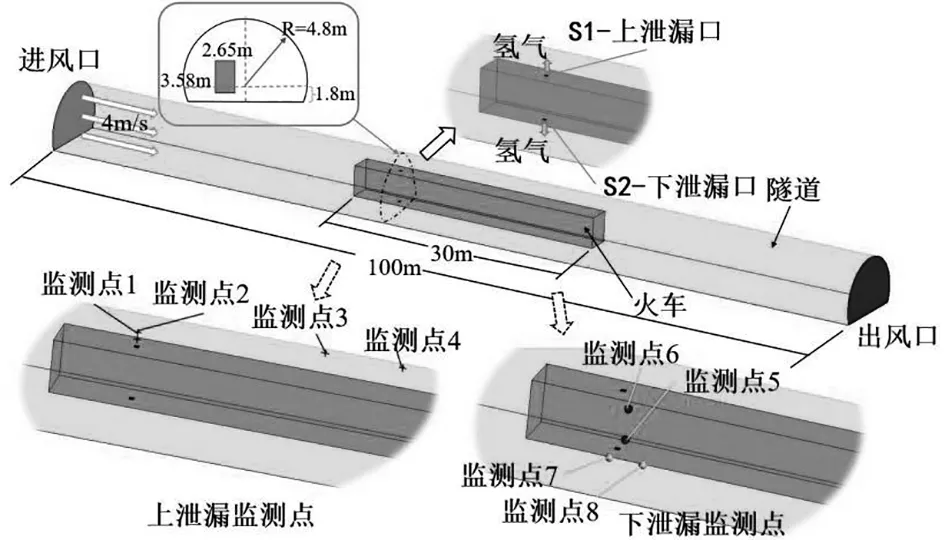
图1 物理模型
泄漏域认为是边长0.305 m的正方形,将其设置为质量流量入口。考虑了纵向通风作用,隧道口为进风区,设置为速度入口。假设列车行驶至隧道中心处开始以恒定速率发生泄漏(较为危险状态),质量流量为83.3 g/min,H2连续泄漏;环境压力为大气压力,温度为20 ℃,且隧道有4 m/s的纵向流动风。建立隧道的几何模型并进行网格划分,图2为隧道进风口网格情况,此模型网格为结构化网格。网格尺寸从泄漏口逐渐向两侧变大,并将泄漏口周围的网格进行加密。网格对仿真结果有很大的影响,合理的网格划分极其重要。这里为保证仿真的准确性,通过网格无关性验证,选择了348万网格进行求解[10]。

图2 隧道进口网格
1.2 数值模拟计算方法
本文应用计算流体动力学软件对隧道内列车H2泄漏进行模拟[11]。该软件应用有限体积法离散流体流动控制微分方程。基于Realizablek-ε湍流模型和组分运输模型,Realizablek-ε模型是在标准k-ε模型的基础上进行改进,引入了旋转和曲率相关内容,可应用于模拟气体的湍流流动[12]。
H2的泄漏扩散数值模拟,遵循连续性方程、动量方程、能量守恒方程。
(1)连续性方程
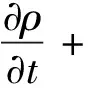
(1)
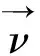
(2)动量方程

(2)
(3)

(3)能量守恒方程
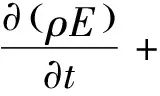

(4)
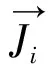
(4)湍流模型
Realizablek-ε模型中,湍流动能k及其耗散率ε由以下方程求得:
(5)
(6)
式中,Gk为由于平均速度梯度而产生的湍流动能;YM为可压缩湍流中波动扩张对总耗散率的贡献;C1、C2和C1ε为常数;μt为湍流粘度;σk和σε分别为k和ε的湍流普朗特数。
(5)组分输运方程
组分输运方程表示为系统中组分质量的变化率,该变化率等于通过系统界面的净扩散通量与化学反应中组分的产生率之和。可认为H2分散系统仅包含H2和空气2个成分。

(7)
式中,ρ为系统中H2或空气的密度;Yi为物种i的质量分数;Ri和Si分别为物种i的净生产率和由用户定义的源项和离散项引起的额外生产率。
2 模型验证
采用刘秀秀[13]的N2在CO2中泄漏扩散实验进行模型验证。实验空间为2端开口、4面封闭的半封闭空间长方体。图3比较了模拟与实验中监测点N2时变的体积分数。可以看出,模拟中的形态趋势和实验中的一致。N2的体积分数在释放时均有向上增长的趋势,在67~85 s时体积分数趋于稳定增长,并与实验结果保持几乎相同的增长速度。其中模拟和实验结果的偏差可能是测量误差等不确定因素造成的。综上,CFD模型是可行且有效的。

图3 实验和模拟N2体积分数对比
3 结果和讨论
本章分析2种泄漏工况下H2释放和扩散的变化规律。基于H2爆炸下限浓度4%的等值面进行分析。S1泄漏口释放时,其周围的浓度值较大,由于风速和天花板的作用,H2云沿着隧道顶部向隧道出口处扩散,并被流动风和持续释放的H2沿着顶部推动,在顶部周围形成易燃层。t=20 s时,H2扩散至隧道出口,H2在泄漏过程中形成H2-空气混合层,混合层可能会形成氢爆炸云团,造成极大的危险。H2泄漏后在天花板形成的可燃气体云轮廓不规则且相对于长时间的扩散其波动值较大。泄漏一段时间后,如t=110 s时扩散速度稳定,扩散到各方位的H2浓度变化不大并且扩散区域大。对比之前时间的泄漏来说,各方位的H2浓度增大,可燃气体云的轮廓增大,危险程度大于以上情况。分析表明,如果不采取缓解措施,在隧道顶部会积聚大量的H2,存在较大风险。
通过分析可知,S2泄漏危险程度较大,因为H2沿车身扩散浓度较高,在列车底部可能会形成氢爆炸云团,风险较大。在泄漏初期人员可选择向进风口的方向撤离,以确保人员安全。当t=20 s时,H2扩散到列车尾部,由于风速的作用,大部分H2还会沿原来方向扩散,又因其扩散范围受车尾漩涡及浮力的影响而变大,此时在列车尾部形成H2高浓度回流区。当t=110 s时,S2泄漏的H2大规模积聚在列车尾部,由于列车上部和下部都受流动风的影响,扩散到列车尾部的气体会向顶部和隧道出口处不断扩散,此时可燃气体云的轮廓变化相对稳定。
图4显示了S1和S2周围各监测点处H2浓度随时间变化情况。各泄漏点位置见图1。释放初始阶段,泄漏以高动量为主,S1处监测点1很快监测到较高浓度的H2,经过一段时间后H2浓度变化相对稳定。随后监测点3和4处的浓度由于通风和顶部的作用在初始检测时不平稳,但很快检测到气体,然而浓度相对监测点1较低,一段时间后均达平稳。S2释放H2时周围监测点也很快检测到气体,由于高动量、浮力和风速的作用,初始阶段浓度扩散不稳定,使得监测点8处监测到H2波动较大,扩散一段时间后达到平稳。从监测点的数值可以看出,泄漏口周围的H2浓度更高,在此处很容易形成易燃易爆区,其风险较大。
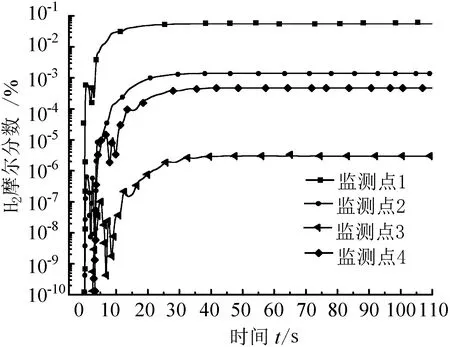
(a)监测点1、2、3、4
4 结论
本文对隧道环境中列车压缩气体系统泄漏的H2进行了计算流体动力学分析,有效识别了列车在隧道中H2罐意外泄漏时带来的风险。首先,利用软件对H2泄漏进行模拟,详细展示了H2在受限空间中泄漏特性;其次,探讨了隧道内纵向通风和不同位置泄漏对气体扩散分布的影响;最后,从浓度范围分析H2在隧道内积聚的后果。主要结论如下:
(1)H2在半封闭空间释放后,上浮扩散,会迅速往隧道顶部和列车底部积聚,使得顶部和底部区域H2浓度较高,危险性大,人员安全撤离时应尽快离开此区域。
(2)泄漏源位置的不同,其所处的风速相同。在初始阶段,S1和S2 2种泄漏工况下,气体扩散受不同障碍物的影响。气体向下游扩散时,其浓度值越来越低,尽管其H2浓度安全限值不同,但是仍然高于安全限值。模拟结果可用于制定H2安全问题的缓解策略。
