考虑网络通信时延的智能网联汽车横向鲁棒控制研究

曹青松, 易 星, 许 力

(1. 江西科技学院 人工智能学院, 江西 南昌 330098; 2. 江西科技学院 协同创新中心, 江西 南昌 330098)

0 引言

智能网联汽车搭载了先进的传感、计算和执行设备，融合了现代通信和网络技术，实现人、车、路等信息的共享交互，是智能车辆和车联网技术的有机结合[1-2]。智能网联汽车横向网联控制的场景应用通常包括：单车的路径引导、紧急避障，以及多车的协同换道、协同避障。车联网技术本身存在的通信时延、丢包等不利因素容易对智能网联汽车横向联网控制的场景应用造成不良影响，其中，车载网络通信时延受到发射机组包与调度、接收机解包等因素的影响；通信丢包受到空口传输速率、接收机灵敏度、信道环境等因素的影响[3]。因此，在研究智能网联汽车横向网联控制过程中，有必要考虑车联网的通信时延对系统造成的影响，从而提高智能网联汽车的横向稳定性和跟踪效果[4]。

智能网联汽车横向控制的相关研究通常忽略了网络通信时延和丢包特性，集中于控制算法方面的仿真与试验研究。冀杰等采用模糊逻辑和滑模控制理论，研究自动驾驶车辆纵向和横向运动的综合控制方法，改善了车辆的跟踪和运动性能[5]；陈无畏等构建智能车辆的横向控制闭环系统，设计并优化模糊控制器，提高了车辆横向控制系统性能[6]；文献[7]提出一种基于模型预测的自动驾驶汽车路径跟踪控制方法，试验验证了方法的有效性；文献[8]研究一种自动驾驶汽车串级纵横耦合控制器，仿真验证不同附着系数下车辆的跟踪精度和稳定性；文献[9]设计带有前馈控制的改进LQR控制器，仿真研究自动驾驶汽车的横向控制，结果表明横向距离和航向角的偏差得到有效控制。然而，通信时延与丢包特性在网络控制系统的研究中引起不少学者的关注。王宝凤等研究Markovian时延与丢包的离散系统，并设计基于跳跃线性的估计器[10]；Lei等对不同通信频率、通信时延与丢包对车辆队列间距的稳定性进行了研究[11]；安宝冉等提出一种时延与丢包补偿机制的预测控制器，提高了网络智能系统的性能[12]；文献[13]仿真研究了通信时延与丢包因素对车辆队列稳定性控制参数的影响；文献[14-15]研究时延与丢包对网络控制系统稳定性的影响。

综合上述相关研究背景，本研究考虑智能网联汽车在网络通信中存在的时延问题，以路径跟踪场景为例，研究智能网联汽车横向网联控制。通过建立含通信时延的车辆操纵动力学模型，设计一种鲁棒控制器，并对控制器参数进行优化，从车辆的横向稳定性和跟踪效果两方面考虑，选取横摆角速度、质心侧偏角、航向角误差、横向距离误差为评价指标，仿真验证所设计鲁棒控制器的控制效果，并分析不同通信时延对车辆横向控制性能的影响规律。

1 智能网联汽车横向控制系统概况

智能网联汽车横向控制系统主要由车体姿态传感器、期望路径生成模块以及横向控制器等组成，如图1所示。

图1 智能网联汽车横向控制系统框图Fig.1 Block diagram of lateral control system of intelligent connected vehicle

智能网联汽车横向控制是通过通信网络实现传感器、控制器与执行器之间的信息传递。在智能网联汽车横向控制过程中，横向动力学控制器根据车辆传感器检测到的侧向速度v、横摆角速度r、航向角偏差φe和横向距离误差de等信息，结合给定的期望跟踪路径，根据一定的控制策略，确定合适的车辆前轮转角δ，以抵抗车辆运行过程所遇到的空气阻力等干扰，不断优化跟踪效果和保证车辆运行稳定。

2 车辆横向动力学建模

2.1 两自由度汽车操纵动力学模型

为了便于研究，假设智能网联汽车行驶的路面平坦，车辆为刚性结构体，忽略转向与悬架系统、轮胎载荷变化、空气动力的影响，建立两自由度汽车操纵动力学模型，如图2所示。

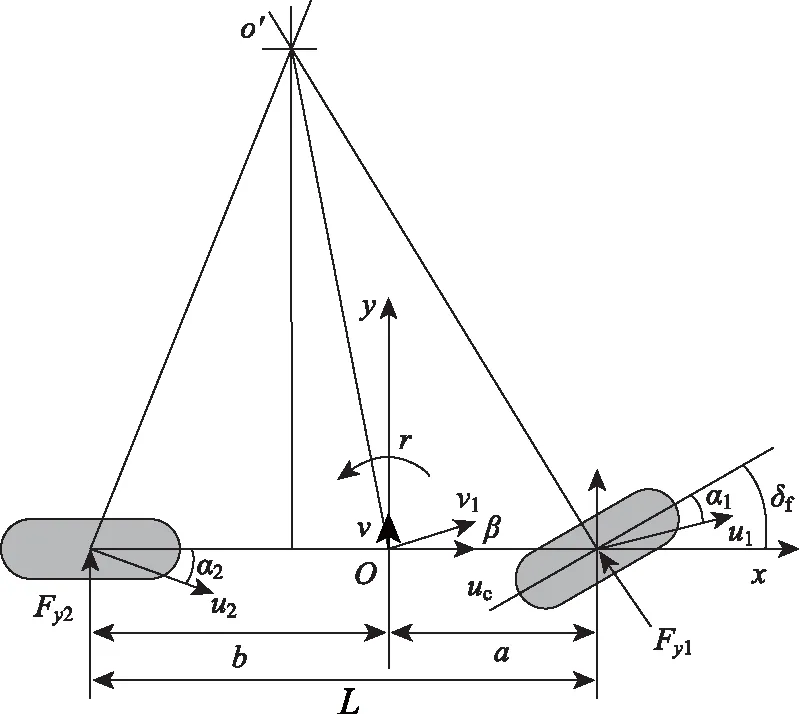
图2 两自由度汽车操纵动力学模型Fig.2 Handling dynamics model of 2-DOF vehicle

图2中，O为车辆质心位置；o′为车辆转向中心；Fy1，Fy2为地面对前、后轮的侧向反作用力；α1，α2为前、后轮的侧偏角；u1，u2为车辆前、后轴中点的速度；uc，v为车辆质心的纵向、横向速度；r为横摆角速度；β为质心侧偏角；δf为前轮转角；a，b为车辆质心到前、后轴的距离。

根据两自由度汽车操纵模型，采用牛顿第二定律推导得到两自由度汽车运动方程：

(1)

Fy1，Fy2的表达式如下：

(2)

α1，α2的表达式如下：

(3)

将式(2)和式(3)代入式(1)中，进一步得到系统运动方程。

(4)

式中，m为汽车质量；Cα1，Cα2为前、后轮胎的侧偏刚度；I为整车绕Z轴的转动惯量。

2.2 考虑通信时延的模型转化

在智能网联汽车横向控制中，车载网络通信通常是离散系统的信息交互，而通信时延是数据因网络连接中断或网络阻塞造成的数据传输滞后，容易对系统造成破坏，使系统出现不稳定的情况。以下考虑网络通信时延，对系统动力学模型进行转化。

对于网联横向控制，以网联路径跟踪应用为例，结合文献[16]，忽略扰动输入，使用状态反馈转角控制，通过零阶保持器以采样时间T离散化，将运动方程(4)转化成如下离散系统：

(5)

式中，A，B，P均为系数矩阵；K为线性状态反馈控制器增益；k为时间序列。

以φ(k)为系统的初始条件，可将上式写成与式(5)形式相同的且具有通信时延的网络控制系统：

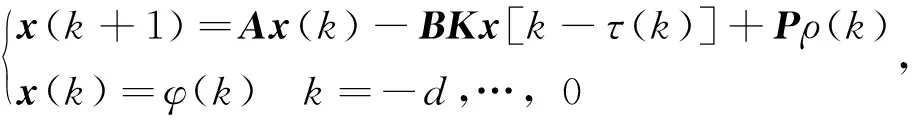
(6)

式中，x(k)=[v(k),r(k),ψe(k),de(k)]T；v(k)为侧向速度；r(k)为横摆角速度；ψe(k)为航向角误差；de(k)为横向距离误差。另外，K为线性状态反馈控制器增益；τ(k)为通信时延周期数或时变丢包持续周期数；d为最大时延周期数或最大丢包周期数；φ(k)为初始条件；lp为预瞄距离；ρ(k)为道路曲率。

式(6)中的系数矩阵如下：

3 车辆鲁棒控制器设计

针对上述考虑通信时延的网联横向控制离散系统，本研究根据Lyapunov泛函方法，结合Finsler引理，并采用线性矩阵不等式方法，设计一种鲁棒状态反馈控制器[17-18]，具体如下：

(7)

XB=BX1，

(8)

式中，

τ=dM-dm，

Θ11=P+dM(Z1+Z2)-X-XT，

Θ22=-P+dM(Z1+Z2)+(1+τ)Q+R+δα2FTF，

Ξ2=[0M+N-M+S-N-S0]

式中，dM，dm分别表示时间上限和下限；I为单位矩阵。

则闭环系统(6)是渐近稳定的鲁棒系统，此时控制器增益为：

(9)

4 仿真研究

4.1 车辆基本参数

以某型普通乘用车为例，采用MATLAB软件开展仿真研究，表1为车辆基本参数。

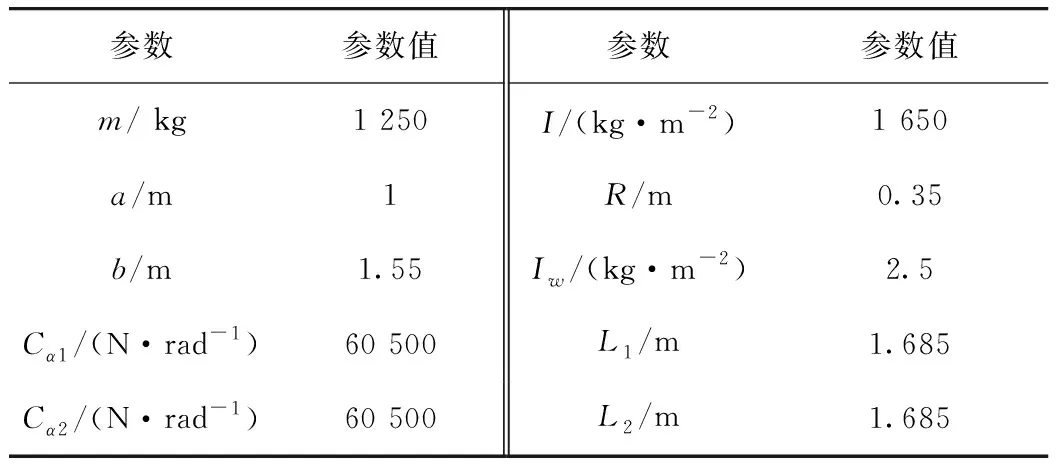
表1 车辆基本参数Tab.1 Basic parameters of vehicle

4.2 仿真步骤

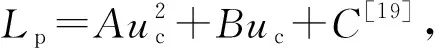
(2) 控制器关键参数K的计算。选定采样时间t=1 ms，采用MATLAB对系统(6)进行离散化处理，通过线性矩阵不等式(LMI)求解控制器最优参数K，进而得到反馈控制器。

(3) 设置离散系统时延τ=0,100 ms,200 ms，仿真观察v,r,ψe,de输出曲线，分析不同时延情况下系统的响应；设置车速uc=60 km/h,100 km/h等，研究不同车速下，控制器对通信时延的鲁棒特性。

4.3 仿真分析

根据上述仿真步骤，分别从道路曲率，反馈控制器参数优化结果，通信时延条件下车辆稳定性、路径跟踪效果以及不同车速下控制器的鲁棒性5个方面进行仿真分析。

(1) 道路曲率分析

道路曲率是车辆横向控制中的输入参量之一，文中采用曲率为阶跃变化的道路进行仿真研究，图3为仿真道路物理形态。其中，开始定义道路曲率为0.05，模拟顺时针方向的圆弧道路，再定义曲率为0，模拟直线道路，定义曲率为-0.05，模拟逆时针方向的圆弧道路，最后，定义道路曲率为0，模拟直线道路。

图3 仿真道路物理形态Fig.3 Physical shape of simulation road

(2) 鲁棒控制器参数优化结果

通过求解线性矩阵不等式，得到鲁棒状态反馈控制器的最优参数K,α和F，如下：

K=[-5.997 0, -9.772 6, -8.389 1, -0.642 3],

α=2,

F=[0.2, 0.2, 0.3, 0.001]。

当鲁棒状态反馈控制器参数设置成上述优化后的值时，含通信时延的系统可以取得较好的控制输出效果。由此，进一步地分析通信时延条件下智能网联汽车的横向控制效果，其中，选择横摆角速度和质心侧偏角为车辆稳定性的评价指标；选择航向角误差和横向距离误差为车辆跟踪效果的评价指标。

(3) 时延条件下车辆稳定性分析

理论上，当车辆的质心侧偏角较小时，通过横摆角速度分析车辆的转向特性，可以有效地判断车辆的稳定性；当质心侧偏角较大时，横摆角速度不能准确描述车辆的稳定性，常通过质心侧偏角来描述。横摆角速度和质心侧偏角是描述车辆稳定性的关键指标参数。

图4为时延τ=0,τ=100 ms,τ=200 ms下的车辆稳定性指标参数响应曲线，其中，图4(a)、图4(b)分别表示横摆角速度、质心侧偏角的响应曲线。

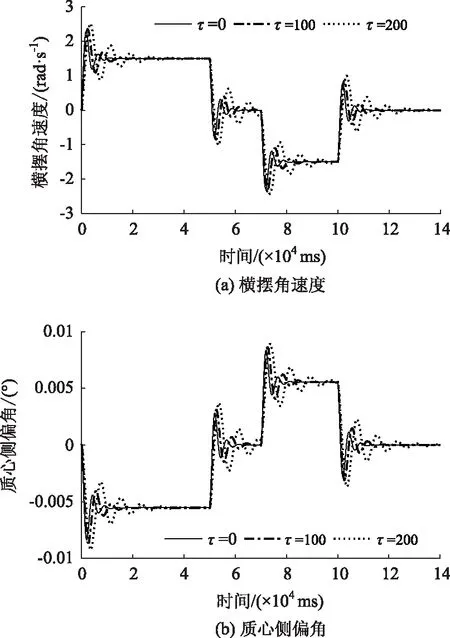
图4 车辆稳定性参数响应曲线Fig.4 Response curves of vehicle stability parameters

由图4(a)、图4(b)可知，横摆角速度、质心侧偏角与道路曲率的变化趋势符合实际，其变化范围分别保持在3 rad/s和0.01°的范围内变化，在路径曲率突变的拐点处，有一定幅度的波动但收敛较迅速，表明所设计的反馈控制器可以较好地控制横摆角速度和质心侧偏角，一定程度保证了车辆的横向稳定性能。

另外，时延τ=0时，横摆角速度和质心侧偏角的幅值变化最小，收敛速度最快，而当时延τ=200 ms 时，在道路曲率的转折点处，横摆角速度和质心侧偏的收敛时间都大于2×104ms，且幅值也有所增大，表明随着时延的增加，会降低车辆的稳定性。进一步研究发现，当时延τ超过300 ms时，横摆角速度和质心侧偏角出现发散，车辆将丧失横向稳定性。结果验证了通信时延会降低智能网联汽车的横向稳定性，且随着时延的增加而变差。

(4) 时延条件下车辆路径跟踪效果分析

智能网联车辆横向控制过程中，确保横向稳定性的前提下，应该尽可能的降低车辆航向角误差及横向距离偏差，从而提高智能网联车辆的路径跟踪精度。

图5为时延τ=0,τ=100 ms,τ=200 ms下的车辆路径跟踪效果参数响应曲线，其中，图5(a)、图5(b)分别表示车辆航向角误差及横向距离误差的响应曲线。

图5 车辆路径跟踪效果参数响应曲线Fig.5 Response curves of vehicle path tracking effect parameters

分析图5(a)、图5(b)可知，车辆航向角误差在±2°范围内波动，横向距离误差则保持在±150 mm 内变化，同样的，在路径曲率突变的拐点处，航向角和横向距离的误差均有一定幅值的波动，但收敛速度较快，而且在不同曲率段，航向角和横向距离稳定后的误差相差很小。结果表明，反馈控制器不但可以有效控制车辆的横向稳定性，还能够保证路径跟踪精度。

从时延的角度分析，τ=0时的车辆航向角和横向误差控制的最好，随着网联汽车通信时延的增加，误差振荡明显，如τ=100 ms,200 ms时对应的误差曲线。研究中也发现，随着通信时延的增加，航向角和横向距离的误差最终不受控制，由此证明时延条件下，随着时延的增加，会降低网联汽车的路径跟踪效果。

(5) 不同车速下控制器的鲁棒性分析

通常情况下，车辆在高速行驶时更容易丧失稳定性，根据上述研究，考虑网络时延的临界值τ=300 ms，以网络时延τ=300 ms为例，分别设置车速uc=30,60,100 km/h进行仿真，得到不同车速下的车辆稳定性参数响应曲线，如图6所示。其中，图6(a)、图6(b)分别表示横摆角速度、质心侧偏角的响应曲线。

图6 不同车速下车辆稳定性评价参数响应曲线Fig.6 Response curves of vehicle stability evaluation parameters at different speeds

由图6(a)、图6(b)可知，在通信时延τ=300 ms的临界条件下，随着车速的增大，横摆角速度和质心侧偏角在路径曲率突变的拐点处，幅值振荡增大，收敛时间延长，尤其当速度超过100 km/h时，稳定性评价参数响应发散，系统丧失稳定性。结果表明，控制器在车速不超过100 km/h时，能够保证车辆的稳定性在可控范围内，即所设计控制器保证系统鲁棒性的车速临界条件为100 km/h。

同理，对不同车速下车辆路径跟踪效果参数响应进行仿真分析，得到同样的结论，文中不进行赘述。

5 结论

(1) 建立了两自由度车辆操纵模型，考虑智能网联汽车的通信时延问题，将车辆操纵模型转换成以道路曲率为输入的状态空间方程，并进行离散化；设计了鲁棒状态反馈控制器，通过求解线性矩阵不等式得到最优的控制器参数。

(2) 仿真得到K等反馈控制器参数；以阶跃曲率为输入，仿真分析横摆角速度、质心侧偏角、航向角误差和横向距离误差的响应，结果表明，控制器能提高智能网联汽车的横向稳定性，同时在路径跟踪控制方面也有较好的效果；此外，验证了网络时延会降低车辆的稳定性和路径跟踪效果，且随着时延增加，容易导致车辆的横向控制失去稳定；在车速不超过100 km/h的条件下，控制器具有较好的鲁棒性。

(3) 本研究考虑通信时延的智能网联汽车横向控制，可以提高智能车辆在路径跟踪行驶时的横向稳定性和跟踪精度，为智能网联汽车在横向控制关键技术方面的研发提供一定借鉴与参考。