大跨波形钢腹板连续箱梁桥有效分布宽度研究

2022-03-21刘旭政荆伟伟

公路交通科技 2022年2期

刘旭政，程坤,2，吴刚，荆伟伟

(1. 华东交通大学土木建筑工程学院,江西南昌 330013； 2. 湖北交投智能检测股份有限公司,湖北武汉 430051；3. 嘉善县交通运输局,浙江嘉兴 314100)

0 引言

近年来随着我国大力推进钢结构桥梁建设，波形钢腹板组合箱梁桥发展迅速。截止2020年年底我国已建成波形钢腹板组合箱梁桥近百座。与钢筋混凝土箱梁桥一样，波形钢腹板组合箱梁桥的翼板也存在剪力滞效应。目前学者普遍认为钢腹板引起的剪力滞效应较混凝土腹板严重[1]。

对于薄壁箱梁的剪力滞效应，国内外学者已经系统地完成了相关研究，取得了大量研究成果[2-4]。对于波形钢腹板组合箱梁的剪力滞效应，目前也有学者开展了相关研究。吴文清结合理论分析、数值模拟及模型试验，系统地研究了等截面简支波形钢腹板组合箱梁桥的剪力滞问题[5-6]；周勇超基于最小势能原理、差分法和变分法，研究推导了变截面波形钢腹板梁的剪力滞递推公式，并与工程实测结果进行对比分析[7]；陈水生采用变分法与有限元法对单箱多室波形钢组合箱梁剪力滞效应进行了对比分析[8]；马磊、万水对比分析了单箱三室波形钢腹板箱梁桥的实测数据与有限元计算结果，对其有效分布宽度进行了探讨[9]。

国内外学者对于波形钢腹板组合箱梁剪力滞效应的研究多集中在简支梁桥或者某一特定桥梁剪力滞系数的计算及测试[10-13]，对于大跨度变截面波形钢腹板组合连续箱梁剪力滞效应研究较少涉及[14]，而相关规范对波形钢腹板组合箱梁翼缘有效宽度取值问题也未明确[15]。本研究以某大跨度变截面波形钢腹板组合连续箱梁为依托，系统分析了变截面箱梁几何参数对剪力滞系数的影响，并在此基础上修正了荷载作用形式，提出了基于现行规范的有效分布宽度比修正系数。

1 工程背景

大跨度连续梁桥主跨跨径最佳适用范围一般在80～200 m之间。表1列出了部分我国已建成和在建的大跨度波形钢腹板组合连续梁桥。

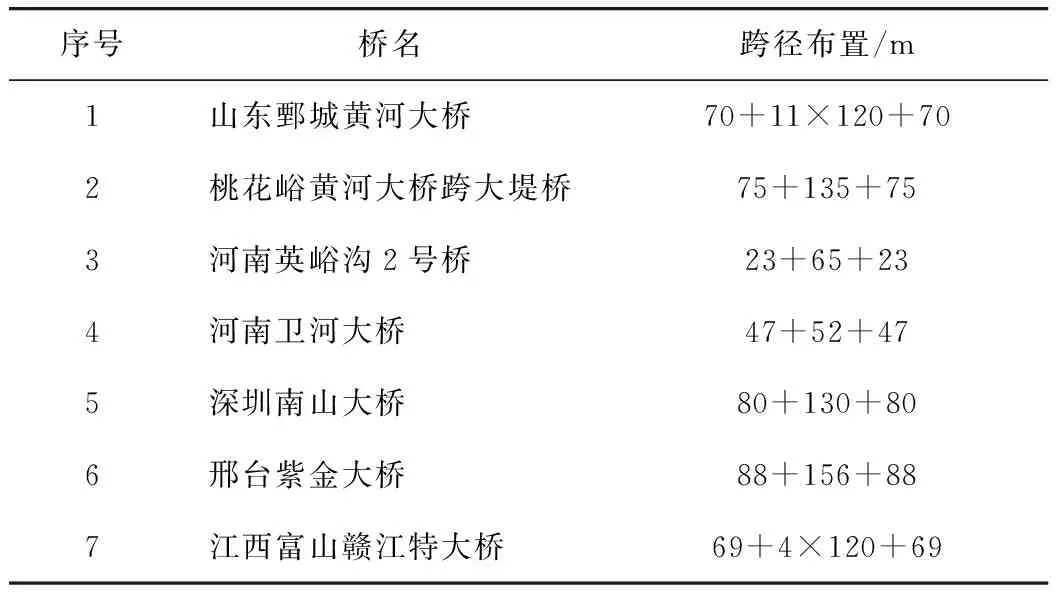
表1 国内大跨度波形钢腹板组合箱梁桥Tab.1 Long-span composite box girder bridges with corrugated steel webs in China

本研究以富山赣江大桥为依托工程[16]，该桥分跨为69 m+4×120 m+69 m，主梁为单箱单室箱梁波形钢腹板组合箱梁。中跨墩顶处梁高7.2 m，跨中梁高为3.5 m。顶板宽16 m，底板宽10 m，翼缘板悬臂长3 m。组合箱梁结构尺寸如图1所示。主梁采用C55混凝土，波形钢腹板采用1600型波形钢板，钢材采用18 mm厚Q345C级合成钢板。

图1 富山赣江大桥典型截面示意图(单位:cm)Fig.1 Schematic diagram of typical section of Fushan Ganjiang Bridge (unit:cm)

2 分析方法

2.1 有限元模型的建立

由于连续跨数量对于箱梁剪力滞效应无直接影响，本研究以典型的三跨式连续箱梁来计算分析其剪力滞效应。采用ANSYS的APDL参数化建模方法建立了(69+120+69) m有限元模型，截面尺寸采用富山赣江大桥实桥数据。混凝土顶、底板均采用8节SOLID45固体单元模拟，波形钢腹板采用4节点SHELL63弹性壳单元模拟。变截面变厚度底板通过“以直代曲”逐段循环建立。波形钢腹板箱梁桥的ANSYS局部模型见图2。

图2 ANSYS局部模型图Fig.2 Diagram of ANSYS partial model

2.2 剪力滞效应的分析方法

采用以下方法计算其剪力滞系数：提取箱梁上、下翼缘板若干个点(每0.5 m设1个数据提取点)的有限元计算出的正应力大小，并求出翼缘板的平均正应力；将上、下翼缘板各点的正应力除以其对应的翼缘板平均正应力，即可得出剪力滞系数。同时采用有效宽度比来考虑波形钢腹板组合箱梁的剪力滞效应。

有效宽度比的定义及计算见式(1)～(3)：

最大剪力滞系数：

(1)

翼缘有效宽度比：

(2)

翼缘有效宽度：

(3)

式中，σmax为翼缘最大正应力；σ0为翼缘平均正应力；b为翼缘的实际宽度；be为翼缘有效宽度。

3 剪力滞效应影响因素分析

关于几何参数对剪力滞效应的影响已有较多研究，除了常规的高宽比、宽跨比、腹板规格(厚度、波高等)的影响，对于变截面的波形钢腹板组合箱梁，主梁高度变化的影响也需要进行分析。计算荷载按一个设计车道布置，集中(均布)荷载横向对称布置于两腹板处。以下各图计算结果以翼缘板中心为坐标原点，箱梁横向各节点位置坐标即为图中横坐标。图例中M代表中跨跨中截面,S代表边跨跨中截面；U代表顶板,D代表底板；P代表集中荷载,Q代表均布荷载；C代表等高截面,V代表变高截面。

3.1 腹板厚度

选取波形钢腹板常用厚度分为16,18(原截面)，20 mm 3种规格对比分析剪力滞系数的大小。集中荷载P作用下的中跨跨中截面及边跨跨中截面的顶板、底板剪力滞系数如图3、图4所示。

图3 P作用下不同腹板厚度的跨中顶板剪力滞系数Fig.3 Shear lag coefficients of top slab at mid-span with different web thicknesses under P action

图4 P作用下不同腹板厚度的跨中底板剪力滞系数Fig.4 Shear lag coefficients of bottom slab at mid-span with different web thicknesses under P action

均布荷载作用下跨中截面的最大剪力滞系数具体数据汇总至表2。

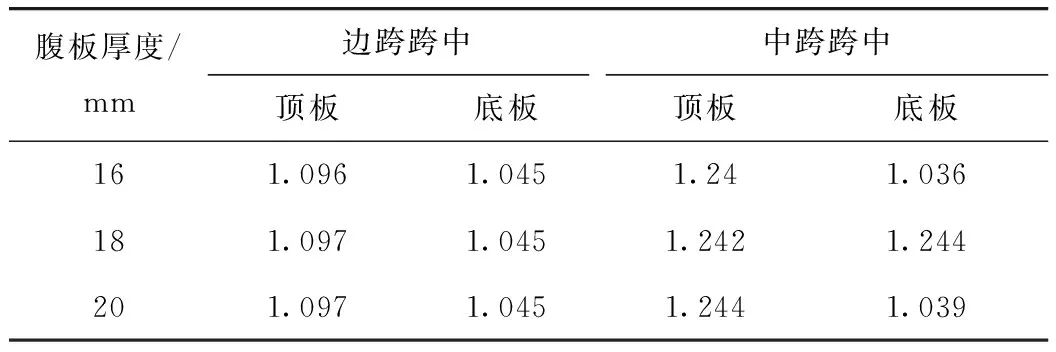
表2 均布荷载作用下跨中截面的最大剪力滞系数Tab.2 Maximum shear lag coefficients of mid-span section under uniform load

随着腹板厚度的增加，中跨及中跨跨中截面顶、底板的剪力滞系数均有所增加，但增加幅度很小，最大增幅为3%。均布荷载作用下的剪力滞系数明显小于集中荷载作用下的剪力滞系数。因此，波形钢腹板厚度对变截面组合箱梁的剪力滞效应影响很小。

3.2 腹板波高

选取波形钢腹板波高分别为0，0.22(原截面)，0.44 m 3种尺寸比较对比分析剪力滞系数的大小。

根据计算结果，中跨截面剪力滞效应小于边跨截面，出于篇幅考虑，本研究以下部分仅列出边跨跨中截面的剪力滞系数计算数据。集中荷载P作用下边跨跨中截面的剪力滞系数如图5所示，从计算结果可以看出：集中荷载作用下，边跨跨中截面顶/底板最大剪力滞系数随着腹板波高的增加均有所降低，最大降幅为6.6%。均布荷载作用下，腹板波高越高，顶板的最大剪力滞系数越小，底板的最大剪力滞系数越大，但整体变化幅度较小。总体来说，波形腹板的波高对变截面组合箱梁的剪力滞效应影响较小。

图5 P作用下不同波高的边跨跨中顶/底板剪力滞系数Fig.5 Shear lag coefficients of top/bottom slab at side span mid-span with different wave heights under P action

3.3 宽高比

考虑到建模的便利性，改变箱梁高度来考虑宽高比的影响。根据已建成大跨度变截面波形钢腹板连续箱梁资料分析，连续梁跨中梁高与主墩墩顶梁高的比值均在0.4～0.67范围内。取墩顶梁高H支=7.2 m不变，分别取跨中梁高H中=0.4H支=2.9 m，原箱梁高度3.5 m以及H中=0.67H支=4.8 m，中间部分梁高按二次抛物线变化,对比分析了3种不同箱梁宽高比在集中/均布荷载作用下截面的顶、底板剪力滞系数，如图6所示。

图6 P作用下不同宽高比边跨跨中顶/底板剪力滞系数Fig.6 Shear lag coefficients of top/bottom slab at side span mid-span with different width-height ratios under P action

集中荷载作用下，边跨跨中截面的顶板的剪力滞系数随着箱梁高度的增加有小幅增加，而底板剪力滞系数小幅减小，最大幅度为5.1%。均布荷载作用下，箱梁高宽比对剪力滞系数几乎没有影响，最大变化幅度为0.3%。总体来看，对于大跨度变截面波形钢腹板组合连续箱梁，箱梁高宽比对剪力滞系数有一定影响，但影响较小。

3.4 宽跨比

对于薄壁箱梁，宽跨比对剪力滞效应影响较大。保持桥跨跨径不变，改变箱梁腹板间距考虑宽跨比的影响。顶板宽度取13，14，15，16(原截面)，17，18 m，对应腹板间距为6，7，8，9(原截面)，10，11 m。对比分析6种不同宽跨比在集中/均布荷载作用下截面的顶、底板剪力滞系数。

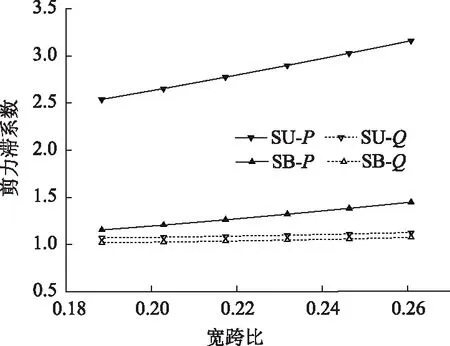
图7 不同宽跨比的边跨跨中顶/底板剪力滞系数Fig.7 Shear lag coefficients of top/bottom slab at side span mid-span with different width-span ratios

从图7可知：集中荷载作用下，随着边跨宽跨比的增加，边跨跨中截面顶板的剪力滞系数从2.538平缓增加到3.157，底板从1.154平缓增加至1.446。均布荷载作用下边跨跨中截面顶/底板剪力滞系数也有所增加，最大增幅为5.3%。

图8 不同宽跨比的中跨跨中顶/底板剪力滞系数Fig.8 Shear lag coefficients of top/bottom slab at central span mid-span with different width-span ratios

从图8可知：集中荷载作用下，随着中跨宽跨比的增加，中跨跨中截面顶板的剪力滞系数从1.472平缓增加到1.703，底板从1.271平缓增加到1.588；均布荷载作用下中跨跨中截面顶/底板剪力滞系数也有所增加，最大增幅为9%。对于大跨度变截面波形钢腹板组合连续箱梁，宽跨比对剪力滞效应影响较大。在集中(均布)荷载作用下，跨中截面的顶板剪力滞系数大于底板剪力滞系数。

3.5 变截面

建立同跨径等截面波形钢腹板组合连续箱梁有限元模型与原变截面模型进行对比分析，荷载类型与加载方式均不变，比较分析集中荷载作用下边跨跨中截面顶/底板剪力滞系数如图9所示。

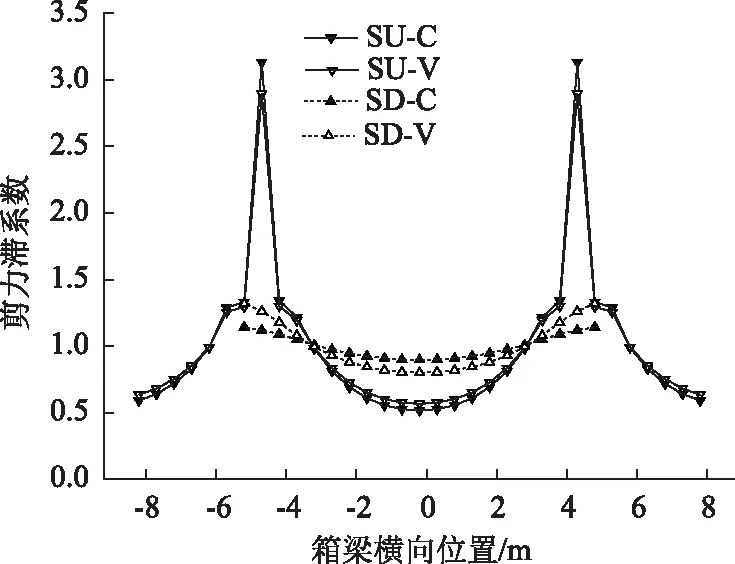
图9 P作用下边跨跨中顶/底板剪力滞系数Fig.9 Shear lag coefficients of top/bottom slab at side span mid-span under P action

从图9可知，集中荷载作用下，等截面连续梁边跨跨中截面顶板的剪力滞系数大于变截面连续梁桥7.6%，底板剪力滞系数小于变截面连续梁桥15.5%。从计算结果可知：集中荷载作用下，等截面箱梁顶板的剪力滞系数大于变截面箱梁，等截面箱梁底板的剪力滞系数小于变截面箱梁。等截面连续箱梁与变截面连续箱梁的剪力滞效应存在较大差异。

3.6 剪力滞效应顺桥向影响范围分析

为了分析剪力滞效应顺桥向影响范围，将集中荷载作用在中跨跨中截面(纵坐标位置为129 m)，荷载作用位置两侧沿顺桥向每隔0.2 m提取截面剪力滞系数，得到集中荷载作用下各分析截面剪力滞系数分布规律如图10所示。

图10 P作用下附近位置的顶板剪力滞系数Fig.10 Shear lag coefficients of top slab at adjacent sections under P action

集中荷载作用在中跨跨中截面时，剪力滞效应在2 m范围内迅速减小，从加载截面的2.896减小到距加载截面0.8 m的1.075，其影响范围十分有限，仅限加载处及附近截面。

4 翼缘有效分布宽度分析

对于大跨度变截面波形钢腹板组合连续箱梁，宽跨比是影响剪力滞效应的主要参数，其他次要参数对翼板的剪力滞效应影响均较小，故在随后探讨翼缘有效分布宽度取值时没有考虑这些非主要因素。

4.1 面荷载对剪力滞大小的影响

根据上述计算结果，集中荷载作用下剪力滞效应更明显，但影响范围十分有限。实际车轮荷载是经过铺装层扩散后以面荷载的形式作用于桥面板的，采用集中荷载计算翼缘有效分布宽度将显得过于保守，影响结构设计的经济性。轮胎与桥面的接触面按规范推荐a2×b2=0.2 m×0.6 m计，假定铺装层厚度H为0.1 m，将集中荷载修正为a1×b1=0.4 m×0.8 m(a1为顺桥向尺寸，b1为横桥向尺寸)的面荷载计算剪力滞系数。分别计算集中荷载、面荷载在中跨不同位置的剪力滞系数，计算模型采用原结构模型,计算出各截面顶板的剪力滞系数如表3所示。

表3 修正荷载前后截面顶板剪力滞系数对比Tab.3 Comparison of shear lag coefficients of top slab of sections before and after load correction

根据计算结果可知，修正前后剪力滞系数变化明显，故可采用修正后面荷载来计算翼缘有效分布宽度。

4.2 有效分布宽度取值研究

将面荷载作用在跨中截面、中墩墩顶截面，同样以加载处截面为分析截面，从分析截面提取结果。与前面一样，分别取腹板间距为6，7，8，9(原截面)，10，11 m，(根据相关资料，现有大跨度变截面波形钢腹板组合连续箱梁宽跨比基本涵盖在此范围内)。为了与现有规范进行比较分析，按宽跨比bi/li计算分析中跨跨中截面、边跨跨中截面、中墩墩顶截面、边墩墩顶截面的有效宽度比，分析在实际车轮面荷载作用下关键截面的有效宽度比变化规律。

从图11可知，随着宽跨比从0.04变化至0.076，集中荷载作用下的中跨跨中顶板有效宽度比从0.847逐渐减小到0.692，底板有效宽度比从0.779逐渐减小到0.624；均布荷载作用下的中跨跨中顶板有效宽度比从0.846逐渐减小到0.776，底板有效宽度比从0.973逐渐减小到0.953。

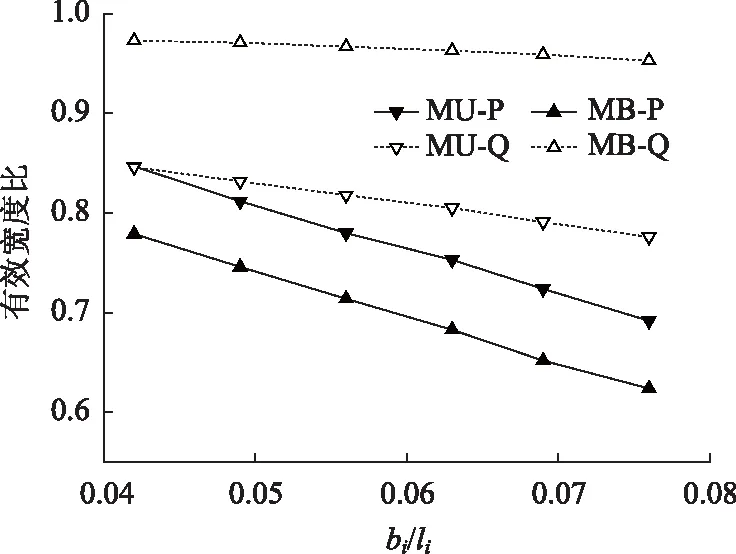
图11 面荷载作用下中跨跨中截面顶/底板有效宽度比随宽跨比变化Fig.11 Effective width ratios of top/bottom slab at central span mid-span section under plane loads varying with width-span ratio

从图12计算结果可知，随着宽跨比从0.054变化至0.1，集中荷载作用下的边跨跨中顶板有效宽度比从0.641逐渐减小到0.457，底板有效宽度比从0.86逐渐减小到0.685；均布荷载作用下的边跨跨中顶板有效宽度比从0.935逐渐减小到0.89，底板有效宽度比从0.982逐渐减小到0.933。

图12 面荷载作用下边跨跨中截面顶/底板有效宽度比随宽跨比变化Fig.12 Effective width ratios of top/bottom slab at side span mid-span section under plane loads varying with width-span ratio

4.3 有效分布宽度修正系数

现行的《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[17](以下简称《公路桥涵混规》)以及《公路钢结构桥梁设计规范》(JTG D64—2015)[18](以下简称《公路钢桥规范》)均给出了箱形截面梁翼缘有效宽度比计算公式。将本研究计算分析结果与规范规定值进行对比，由此提出基于规范的波形钢腹板组合箱梁翼缘有效分布宽度计算的修正系数，修正系数按《公路桥涵混规》考虑，分析结果如表4所示。应当注意的是，规范中提出的有效分布宽度是在设计组合效应下的有效分布宽度，而本研究给出的是单一荷载形式下的有效分布宽度。均布荷载作用下的有效宽度比修正方法同集中荷载，限于篇幅，本研究未给出详细数据。

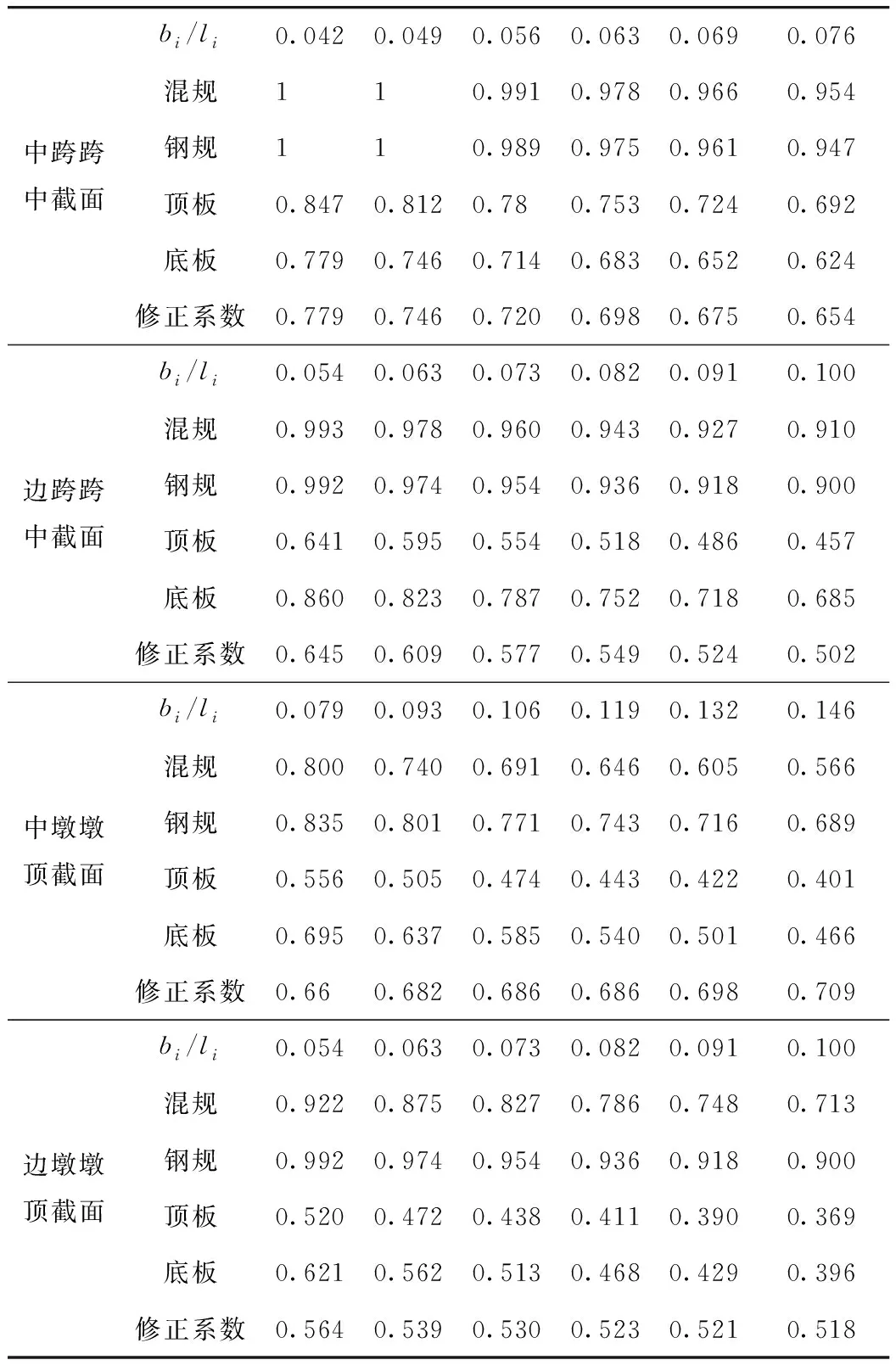
表4 面荷载作用下的大跨度变截面波形钢腹板的有效宽度比Tab.4 Effective width ratios of long-span variable sectional corrugated steel webs under plane loads

根据计算结果可知：在跨中位置，《公路桥涵混规》的有效宽度比的计算结果大于《公路钢桥规范》；而在墩顶位置，《公路桥涵混规》的有效宽度比的计算结果小于《公路钢桥规范》。大跨度变截面波形钢腹板组合连续箱梁在修正荷载作用下的有效分布宽度均小于规范值。中跨跨中截面及中墩墩顶截面的有效分布宽度修正系数取0.65，边跨跨中截面及边墩墩顶截面有效分布宽度系数取0.5。同时，根据结构宽跨的具体大小可参照表格适当调整修正系数。