基于频繁轨迹序列模式挖掘的路径推荐方法
2022-03-21段宗涛任国亮杜锦光王倩倩
段宗涛,任国亮,康 军,黄 山,杜锦光,王倩倩
(长安大学 a.信息工程学院,b.陕西省道路交通智能检测与装备工程技术研究中心,西安 710064)
随着全球卫星导航、物联网、移动通信、大数据等技术与智能交通系统(intelligent transportation system,ITS)的深度融合,城市交通系统已经进入了智能交通时代,越来越多的各类移动对象在不同场景下的时空轨迹数据被采集和存储到时空数据库中。这些时空轨迹数据包含的大量知识需要进行快速有效的分析。在对各种时空轨迹的分析任务中,序列模式挖掘是其中最重要的任务之一。时空轨迹序列模式挖掘作为序列模式挖掘的一个重要研究分支,其可以定义为从海量的、异构的、含噪声的移动GPS轨迹序列中提取潜在的、频繁出现的、具有价值的轨迹序列的过程。通过对这些轨迹序列研究分析可以揭示出有价值的信息来用于广泛的社会服务,如移动模式挖掘[1]、位置预测[2]、路径推荐[3]和异常检测[4]等。
时空轨迹路径推荐作为数据挖掘的一个应用,主要是通过对移动对象的历史轨迹进行挖掘以找出其行为潜在的时空规律性及其行为偏好,以此来为移动对象推荐合理、高效的运动路径。出租车作为城市居民户外出行普遍乘坐的交通工具,其对城市居民的出行生活有着举足轻重的影响,而出租车司机对城市的路网结构以及交通情况有着很深的了解,他们经常利用他们的经验知识在给定起始点-目的地(O—D)的情况下选择行驶路线,这些蕴含经验知识的行驶轨迹往往具有较高的成本效益,如行程距离短、行车时间少、行车速度快等。依据出租车司机的经验轨迹模式来进行路径推荐可以提供更加合理、准确、高效的行驶路线。在此背景下,本研究的目标是提供一种融合经验路线的路径推荐方法,以涵盖出租车司机的行车经验与偏好。当用户给定一个起始点—目的地(O—D)的时候,应该解决以下几个挑战:1)如何将出租车历史轨迹数据中蕴含的经验知识融合到路径推荐过程。2)如何针对给定的O—D进行个性化路径推荐。3)证明路径推荐方法的有效性。
针对以上问题,提出了一种基于频繁轨迹序列模式的路径推荐模型,首先,根据出租车的状态信息(空载或载客)将原始GPS轨迹序列分段为子轨迹序列,并利用经过Map-matching的GPS轨迹数据中包含的城市路网路段信息将出租车GPS轨迹数据转换为一种由道路编码的表现形式,称之为路段ID序列;然后将路段ID序列保存为.json格式的路段轨迹序列数据文件导入到MongoDB数据库中,通过输入起始路段ID、终止路段ID和某个时间段,就可以检索出在该时段内经过这两个路段ID的所有路段轨迹序列。接下来,使用序列模式挖掘算法PrefixSpan[5]挖掘频繁轨迹序列对候选轨迹路径集合进行优先级排序,针对频繁轨迹序列中长短模式对候选路径排序的影响差异较大的问题,提出了一种长短模式权重评估模型,最后,按照排序结果向用户推荐评估值前Top-n的路径。该方法有以下贡献点:
1)提出了一种新的路段历史轨迹序列数据库。将出租车GPS轨迹数据转换为一种由道路编码表示的路段ID序列,然后转换为数据文件并导入MongoDB数据库中生成路段历史轨迹序列数据库,该数据库使得用户可以根据自己的需求快捷地检索轨迹数据。
2)提出了一种基于频繁轨迹序列模式的路径推荐模型。根据用户要求在路段历史轨迹序列数据库中检索出符合条件的路径,然后基于序列模式挖掘方法对候选路径集进行排序,针对频繁轨迹序列中长短模式对候选路径排序的影响差异较大的问题,提出了一种长短模式权重评估模型。
3)依据真实的城市路网交通轨迹数据设定了4个模拟场景,通过模拟案例对该路径推荐方法的分析结果表明,该推荐方法是具备合理性的,其为用户推荐的路径是符合大多数出租车驾驶员行车习惯的,如:行车距离短、行车时间少、平均速度高等;同时与最短路径测试集相比较,推荐算法所推荐的路径更加可靠、稳定;与传统路径推荐算法相比其运行速度更快。
1 相关工作
时空轨迹序列模式挖掘作为序列模式挖掘的一个重要研究分支,旨在从时空轨迹数据集中找出频繁出现的序列模式,如普遍性规律或公共性频繁路径等。本文采用模式增长类算法PrefixSpan来挖掘频繁轨迹序列模式,该算法在保证模式时序性和空间位置关系不变的情况下,能够花费较短的时间挖掘出蕴含出租车司机经验知识的频繁路径。
路径推荐不仅是时空轨迹序列模式挖掘的一个主要应用,在其他技术研究领域也越来越受欢迎。例如,文献[6]提出了一种基于地理标记照片的语义轨迹模式挖掘的轨迹推荐系统,该系统考虑了轨迹的时空顺序和空间语义维度以及用户的偏好约束,从带有地理标记的照片中挖掘频繁的旅行模式,然后提取出一组语义行程向用户推荐。文献[7]提出了一种通过深度神经网络权重学习的上下文感知路径推荐方法,该方法基于深度学习从历史数据中提取与每个路线特征相关的权重知识,应用随机规划模型来解决权重丢失问题,在此基础上通过利用加权最短路径的目标值自定义深度神经网络的损失函数来连接学习方法和优化问题。文献[8]提出了一种基于用户群动态群类的个性化旅游路径推荐系统,该系统使用MapReduce编程模型优化的聚类方法来挖掘小群模式。文献[9]提出了k最短路径算法,在满足用户给定的阈值下,向用户推荐k条彼此足够不同且尽可能短的路径。文献[10]提出了一种基于混合交通模式的出行路线推荐模型,将路线推荐问题转化为旅行路线图中的最短路径问题,相比于传统最短路径推荐模型,改变了单一交通规划的方式,解决了单车出行方式的局限性。上述文献依据路径最短、语义结合、业务需求等方面向用户推荐路径,综上所述,很少有研究考虑过将出租车司机行车经验加入到路径推荐方法中,即使用出租车轨迹数据在指定起点和终点的情况下,考虑出行的起始时间以及出行路径的频率,使用面向O—D和面向路径结合的方法将隐藏在轨迹数据中的知识转化为候选推荐路径。
2 问题建模
本文利用经过Map-matching的GPS轨迹数据中包含的城市路网路段信息,将车辆原始GPS轨迹数据转换为城市路网路段序列,将原始轨迹序列中车辆移动的地理位置、移动方向等空间特征用路段及其之间的顺序来表示,将路段轨迹序列数据文件导入到MongoDB数据库中,得到一个路段历史轨迹序列数据库,通过输入起点、终点和出行时间段搜索得到一个候选路径集,基于各个候选路径中包含的频繁路径序列模式对其进行量化评估并进行排序,取出指定的前Top-n条路径为用户进行推荐。
2.1 路段历史轨迹序列数据库
首先从出租车原始轨迹数据中提取得到载客路段轨迹序列集和空载路段轨迹序列集数据文件,数据文件的格式为.json,其每一条轨迹段数据共包含6个字段信息。
定义一轨迹段ID(TrajectoryID).前10位表示轨迹段起始点的年、月、日、时,第11~14位表示轨迹段起始点的分、秒,统一化为s表示(不超过3 600 s),最后5位为对应出租车的车牌号。
定义二轨迹段状态(State).表示该条轨迹段是空载还是载客(4:空载轨迹段,5:载客轨迹段)。
定义三由路段ID组成的轨迹段序列(Segment)。原始轨迹点通过地图匹配映射到路网中的路段上,不同轨迹点对应的路段ID有可能相同也有可能不同。
定义四路段掩码(Mask).其表示该路段轨迹序列中匹配到各个路段ID上轨迹点的个数。因此Segment和Mask的个数是一一对应的。
定义五时间戳序列(Timestamp).其每一项表示相邻轨迹点之间的采样时间间隔,单位为s,由于起始轨迹点前面不存在轨迹点,故其对应的时间间隔设置为0.
定义六轨迹段的其他信息序列(Other)。其表示由该轨迹段中一系列轨迹点按照先后顺序匹配到路段上的经纬度信息、速度信息、航向角信息组成的序列。
通过将路段轨迹序列数据文件导入到MongoDB数据库中,得到一个路段历史轨迹序列数据库TD1,其结构如表1所示。然后,构造一个路段索引哈希表结构HM,该哈希表的key代表轨迹数据中的路段ID,value为经过该路段ID的所有TrajectoryID,该哈希表结构保存在内存中供检索路段使用,其具体的结构如表2所示。

表1 轨迹段数据表Table 1 Track segment data table

表2 路段索引结构表Table 2 Link index structure table
2.2 基于频繁轨迹序列模式的路径推荐方法
通常情况下,出租车司机相比其他出行群体具有更优的路径选择行为,即其选择行驶的路径往往具有行程距离短、行车时间少、行车速度快等特点,将此称之为驾驶员的经验行驶轨迹;基于大规模出租车历史轨迹数据挖掘出出租车的频繁轨迹序列模式,这些轨迹序列模式即出租车司机的经验行驶轨迹。把这些频繁轨迹序列模式用于为出行者进行路径推荐的过程中,将会为其提供性价比较高的出行路线,从而实现合理化的路径推荐。
对此本文设计了一种路径推荐方法,其主要包括两个阶段:
1)查询阶段。对于给定的起点、终点和出发时间段,通过构建的历史轨迹数据库TD1和路段结构表HM可以搜索出满足给定条件的所有轨迹路径,它们构成了一个候选轨迹路径集合。
2)排序阶段。由于在1)中通过数据库自带的搜索引擎查询出来的各轨迹路径之间的优先级是不得而知的,即哪一条路径更值得被推荐还无法确定,因此设计了一种长短模式权重评估模型对查询出的所有候选路径进行一个优先级排序,然后将排名前n的路径推荐给用户。
本文使用模式增长类算法PrefixSpan算法挖掘出租车的频繁轨迹序列模式,具体算法流程见算法1,由于频繁路段轨迹序列必为轨迹段数据中的子路段序列,即每条频繁路段轨迹序列都会对应一个或多个轨迹段ID信息TrajectoryID,因此在进行结果保存的时候,为每条频繁路段轨迹序列带上其在原始轨迹段数据集中的轨迹段ID信息TrajectoryID,然后以TrajectoryID作为key,其对应的频繁路段轨迹序列集合作为value(若有多条路段轨迹序列,中间用“;”隔开)输出.json文件。
算法1 PrefixSpan算法
输入:序列数据集S和支持度阈值min_sup
输出:所有满足支持度要求的频繁序列集
i=1,αi←findPrefix(i)
S|αi←findProjection(αi)
for each elemLj∈αido
sum_i_Lj=count(Lj)
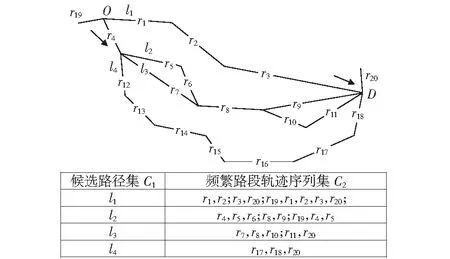
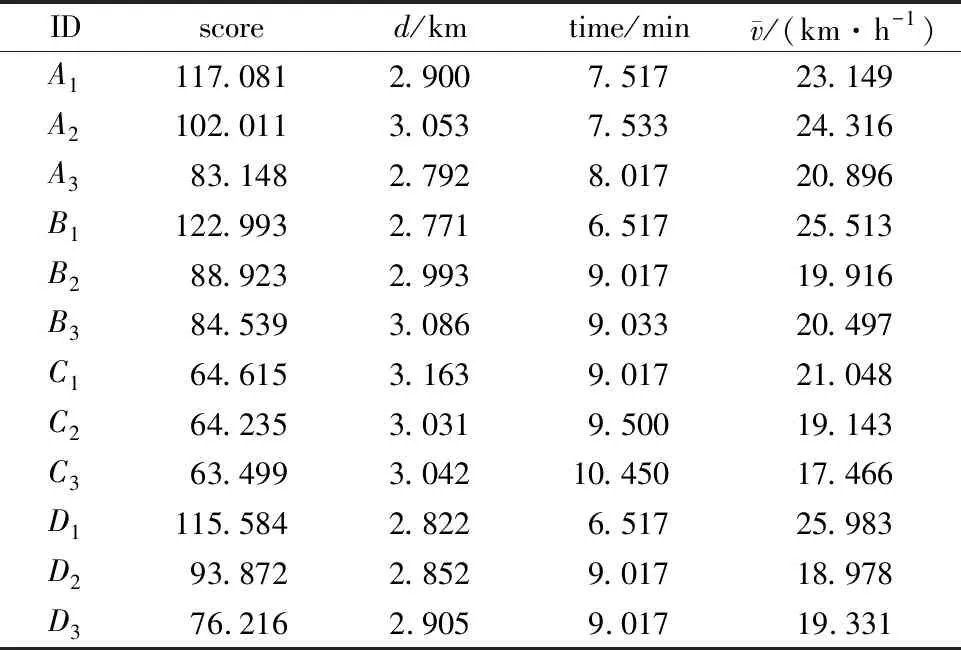
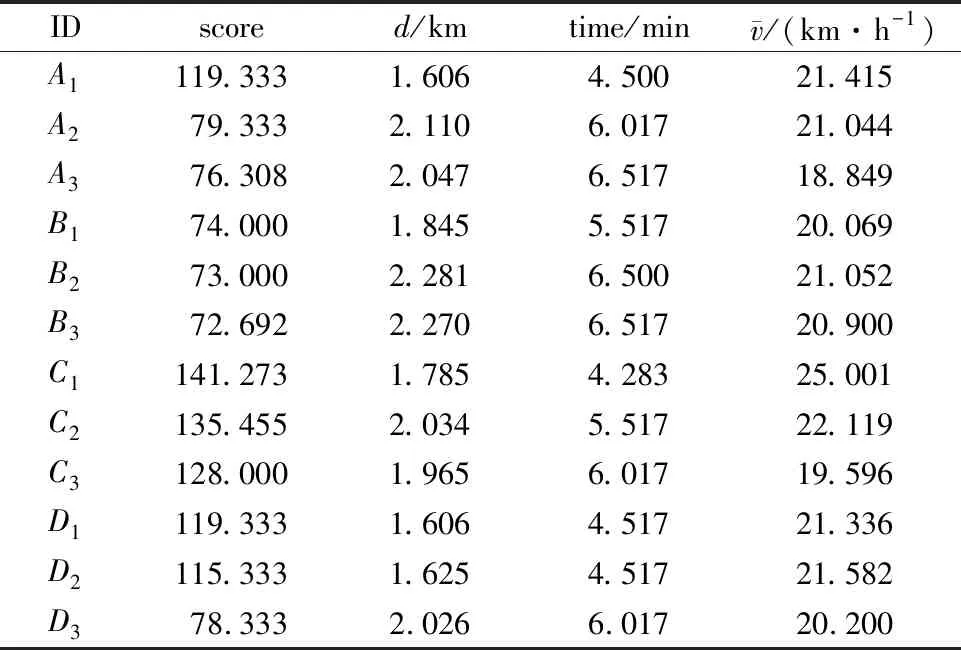
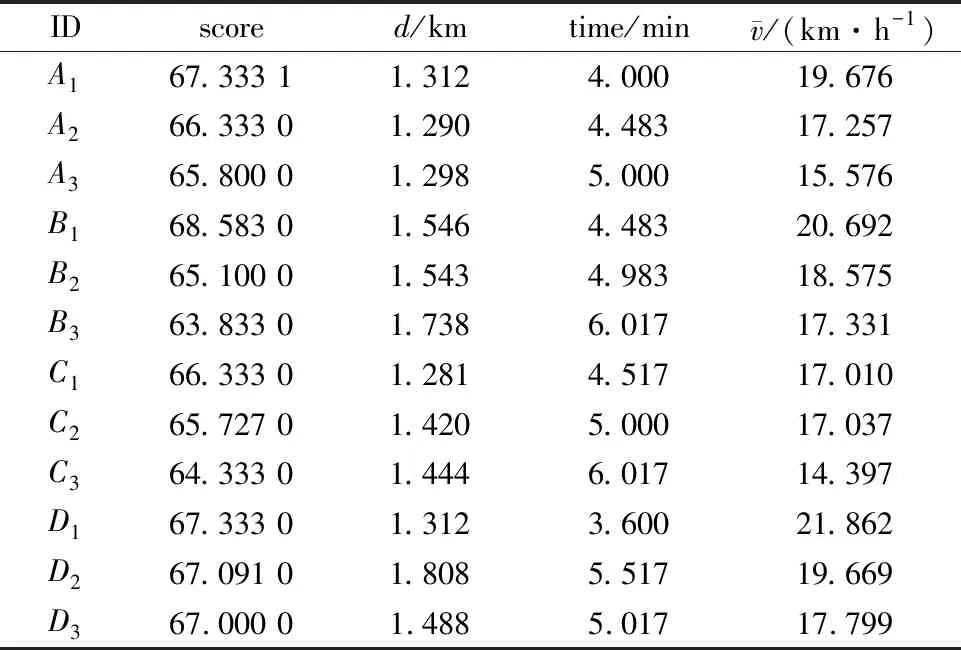
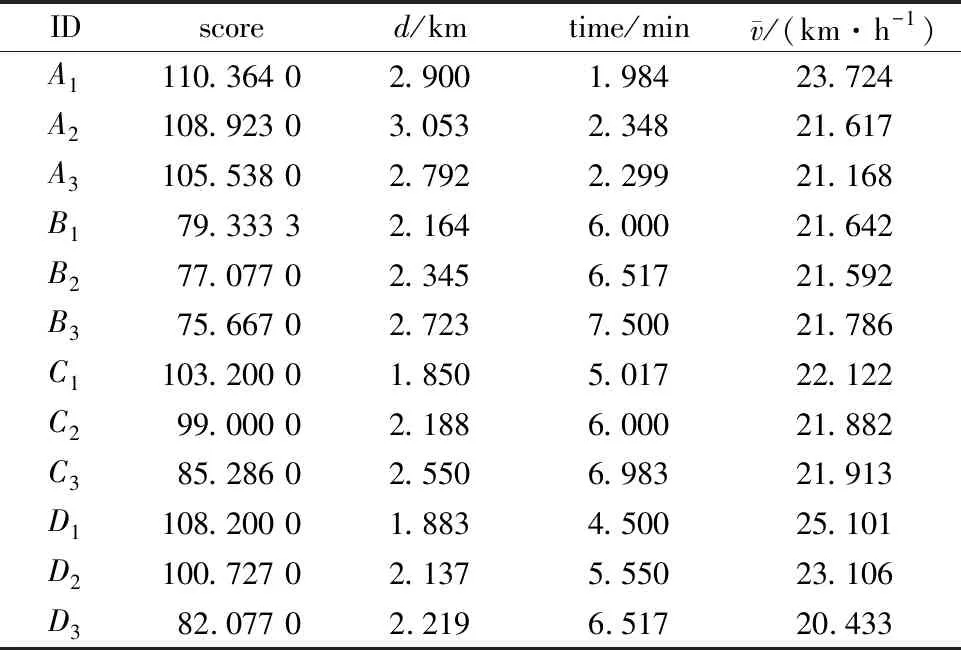
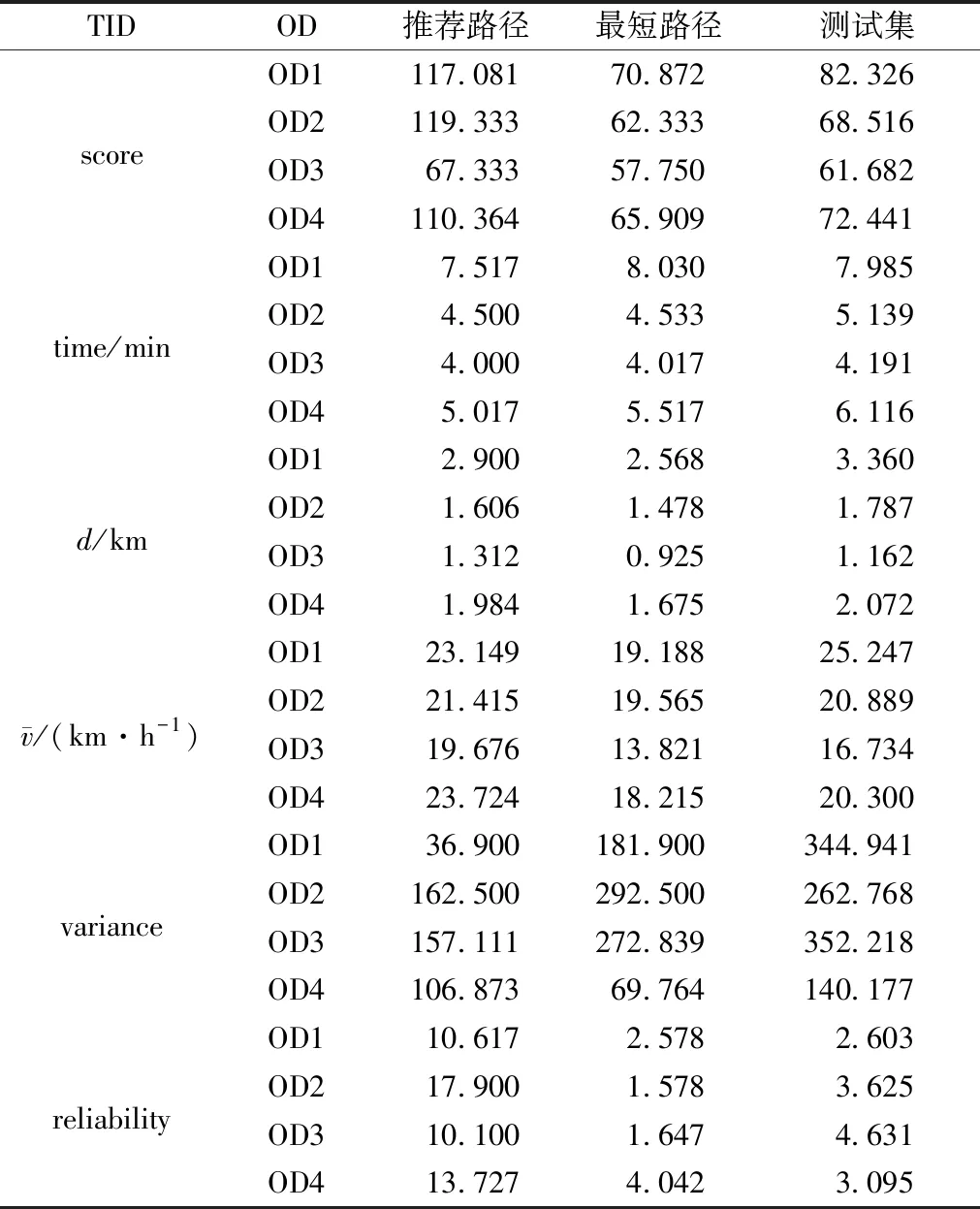
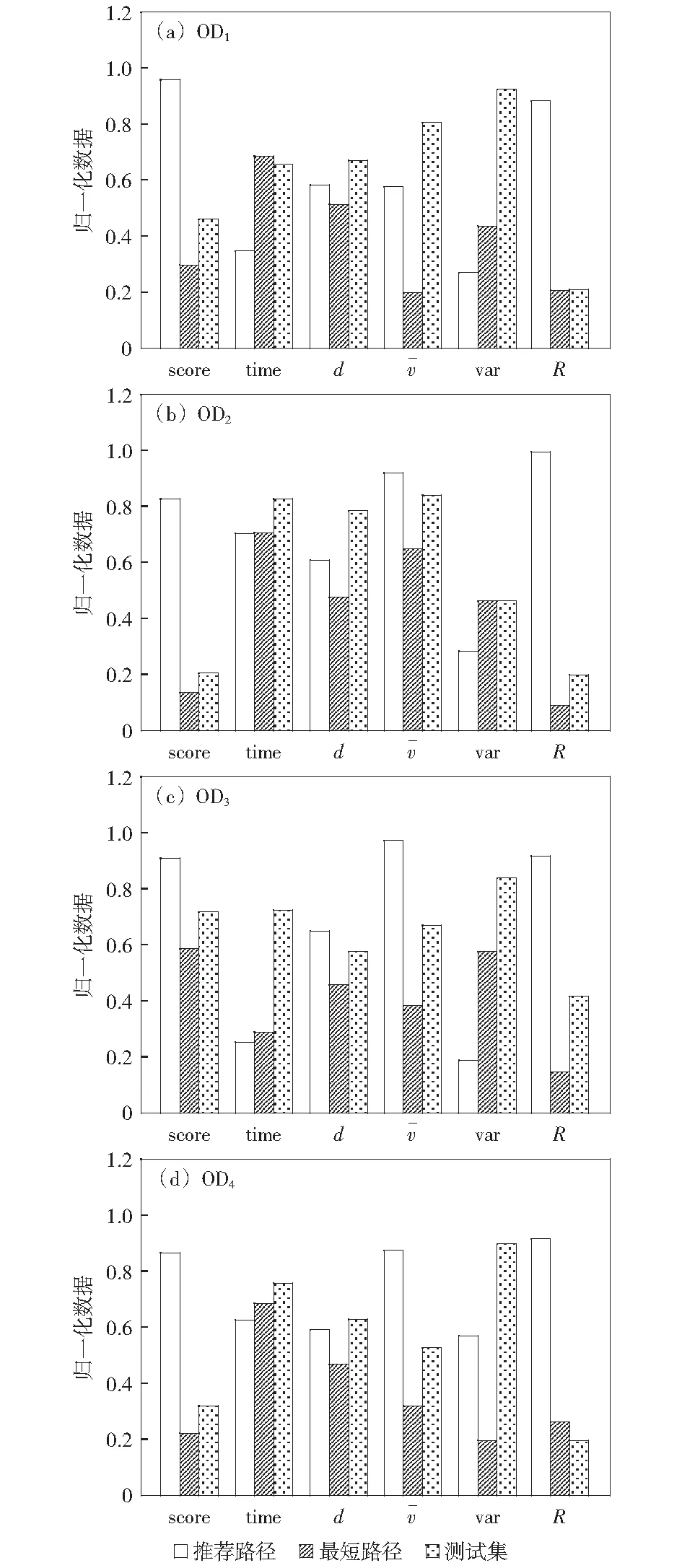
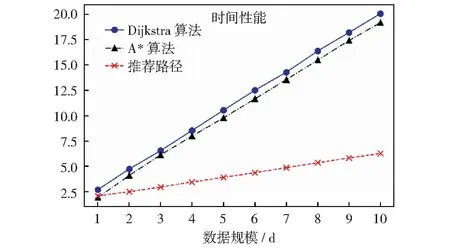
if(sum_i_Lj αi.delete(Lj) end for for each elemLj∈αido S|Lj←findProjection(Lj) if(S|Lj=null ‖ each elem sumiLj∈count(S│Lj) Return 然后,同样将频繁路段轨迹序列数据文件导入到MongoDB数据库中,得到一个频繁路段轨迹序列数据库TD2,如表3所示。通过输入某个轨迹段ID即可得到该轨迹段ID对应的频繁路段轨迹序列集。 表3 频繁路段轨迹序列数据表Table 3 Frequent trajectory data table 接下来,基于构建好的路段历史轨迹序列数据库TD1和频繁路段轨迹序列数据库TD2,对查询阶段的候选路径集合设计了一种排序方法,具体步骤如下: 1)在数据库TD1中输入用户给定的起始路段编号O,通过哈希表HM查找出所有经过起始路段的所有轨迹段ID集startSet,同样,输入终止路段编号D查找出所有经过终止路段的所有轨迹段ID集endSet,然后通过交集运算startSet∩endSet计算出经过这两个路段ID的所有路段轨迹序列,根据用户给定的起始时间t1-t2对其进行过滤得到满足O—D和时间要求的轨迹段ID集合,最后使用数据库TD1查询过滤得到的轨迹段ID,就可以查询出经过O和D并且满足时间要求的所有路段轨迹序列及其对应的轨迹段ID,将其称为候选路径集合C1(C1中的所有轨迹序列仅保留以O开始以D结束的部分)。 2)对于候选路径集合C1中的每一条路段轨迹序列Li,先提取出Li的轨迹段ID,即Ti,然后在数据库TD2中查询出Ti对应的频繁路段轨迹序列集C2. 3)由于C2中每条频繁路段轨迹序列Lj必是原始路段轨迹序列的一部分,因此对于候选路径集合C1中每条路径Li而言,Lj可能存在于Li中,也可能不存在,例如,当Li的长度小于Lj时,肯定不会在Li中匹配到Lj;而频繁路段轨迹序列集C2中的每条频繁路段轨迹序列Lj在候选路径Li中的出现情况能反映出该条候选路径是否更值得被推荐,即对于任意一条候选路径Li而言,其在频繁路段轨迹序列集C2中匹配到的频繁轨迹序列模式越多,尤其是长模式,该路径就越符合出租车驾驶员的出行习惯,越值得优先向用户推荐。 接下来,对C2中每条频繁路段轨迹序列Lj在候选路径Li中进行模式匹配,若Lj完整存在于Li中,则用Lj长度与Li长度的比值表示Lj在Li中的匹配得分,否则,得分为0.最后将所有匹配得分求和即可得到候选路径Li的总得分,其计算公式如式(1)所示。 (1) 4)根据式(1)算出候选路径集合C1中每条候选路径Li的总得分,再根据每条路径的总得分降序排列,取出指定的Top-n条路径为用户进行推荐。 下面以一个例子具体地说明该过程,如图1所示,在指定O—D对之后从数据库中搜索出4条候选路径集合C1,依次为l1={r1,r2,r3};l2={r4,r5,r6,r8,r9};l3={r4,r7,r8,r10,r11};l4={r4,r12,r13,r14,r15,r16,r17,r18},并根据轨迹段ID搜索找到对应的频繁路段轨迹序列集C2,然后遍历处理每一个轨迹段,对于路径l1,遍历他的频繁路段轨迹序列集,{r1,r2}在l1中,得分为2/3,{r3,r20}有一半在l1中这种情况得分为0,{r19,r1,r2,r3,r20}的长度为5大于l1路径长度,得分为0,所以经过计算路径l1的总得分为0.667.路径l2有两个匹配频繁项{r4,r5,r6}和{r8,r9},总得分为3/5+2/5=1.路径l3匹配的频繁项为{r7,r8,r10},匹配得分为3/5=0.6.路径l4搜索到的频繁项只有{r17,r18,r20},不完整存在于路径l4中,所以l4得分为0.最终根据匹配分数对4条路径排序为l2>l1>l3>l4,路径l2推荐给用户的优先级最高,最不推荐用户选择路径l4出行。 图1 路径推荐实例Fig.1 Route recommendation example 具体的算法如算法2所示。 算法2 频繁轨迹序列模式路径推荐算法 输入:起始路段ID编号O、终止路段ID编号D、时间段t1-t2、推荐路径条数n 输出:得分前Top-n条路径 C1←TD1.FindRoute(start=O,end=D,time=t1-t2) for each candidateLi∈C1do Ti←Li.getTrajID() C2←TD2.FindFrequentSet(TrajID=Ti) for each elemLj∈C2do ifLi∈Ljthen Li.score←Li.score+Lj.size÷Li.size end for C1.sortBy(key=Li.score) C1.take(n) 为了评测算法推荐的路径,本文从可靠性、稳定性和合理性3方面来进行评测[11],具体定义如下: (2) 定义八稳定性(Stability)。通过所推荐路线的速度的方差来量化其稳定性,方差越高表示速度的变化幅度越大,行程越不稳定,计算公式如式(3)所示。 (3) 本文采用模拟场景的方式对提出的路径推荐算法进行分析与评估,实验采用2016年9月1日到9月10日11 530辆西安市出租车GPS轨迹数据,轨迹数量为1 000多万条,在进行实验之前对数据进行预处理、轨迹分段和轨迹段编码。假定有4名用户A、B、C、D,用户A在早高峰时段8:00-11:00出行,用户B在午高峰时段14:00-17:00出行,用户C在非高峰时段17:00-19:00出行,用户D在晚高峰时段19:00-22:00出行,并指定了4组起止路段ID,分别为OD1(51483701132,51482708869)、OD2(51482702983,51482702631)、OD3(51483710281,51483701237)、OD4(51483708245,51483703286)。各个OD对所代表的实际地址如表4所示,频繁轨迹序列模式挖掘算法的最小支持度阈值设置为3,n为3. 表4 OD对地址详情Table 4 OD pair address details 这几个位置都处于市中心地区,选择这一领域的考虑因素如下。首先,这几个地区有足够的出租车司机和行驶轨迹数据来支持这路径搜索实验。复杂的交通状况和城市中心地区频繁的拥堵,使得利用经验丰富的司机的路线决策经验是有价值的。其次,由于中心地区人流量大,出租车司机倾向于到中心地区为乘客提供服务,因此,在中心地区可以观察到比其他地区更多的轨迹数据,以支持路径搜索任务。 使用本文提出的路径推荐方法为4个用户针对4组OD对分别进行路径推荐,推荐结果如表5-8所示,此处将轨迹段ID简写为用户ID加编号。 表5 OD1推荐路径属性值Table 5 Attribute value of recommended path at OD1 表6 OD2处推荐路径属性值Table 6 Attribute value of recommended path at OD2 表7 OD3处推荐路径属性值Table 7 Attribute value of recommended path at OD3 表8 OD4处推荐路径属性值Table 8 Attribute value of recommended path at OD4 下面从可靠性、稳定性两个方面证明所提出的路径推荐算法是可取的。将算法推荐路径和最短路径、测试集路径的属性进行比较。指定四组OD对,起止点的设置和上文相同,用户出行时间为高峰时段8:00-11:00,使用加入了历史轨迹信息的Dijkstra最短路径算法寻找最短路径,从历史轨迹中随机选取了50条符合起止点要求和时间要求的路径作为测试集,将其数据属性的平均值作为测试集结果。实验结果如表9所示。 表9 推荐路径和最短路径、测试集比较结果Table 9 Comparison results of recommended path,shortest path,and test set 为了更好地反映推荐路径和最短路径、测试集之间的差异,将实验结果进行归一化处理,如图2所示,可以看出推荐算法推荐的路径的得分要远远高于最短路径和测试集,在4组实验中,推荐路径的旅行时间相较最短路径和测试集快10%~20%,路线距离大体上比测试集短接近于最短路径,稳定性和可靠性远远大于其他两种数据集。具体来说,在OD1中推荐路径的各项属性值都是优于测试集的,对比测试集更加具有合理性、可靠性和稳定性。相较于最短路径,虽然最短路径的长度要比本文算法推荐的路径长度短332 m,但是最短路径花费的时间更长平均速度也更低,说明推荐路径比最短路径更具有合理性。同时最短路径的稳定性比推荐路径低79.7%,可靠性低70.2%,这是因为人们都趋向于选择最短路径到达目的地,这样会导致最短路径上的车流量保持在一个很高的水平,出现交通堵塞现象的概率大大增加,所以距离短的路径不一定路况好,而本文提出的算法考虑了出租车司机的行驶经验(出租车司机会根据路况做出适当的路线决策,从而更快地达到目的地),向用户推荐的路径更加频繁、可靠和适用,虽然该方法没有明确的设计为推荐旅行长度最短、时间最快的路径,但是其推荐的路径具备这些特性。 图2 推荐路径与最短路径、测试集比较(归一化)Fig.2 Comparison of recommended path,shortest path,and test set attributes (normalized) 为了验证本文算法的效率,选择Dijkstra算法和A*算法进行对比实验[12],Dijkstra算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止,A*算法使用了一个特别的估价函数f(n)=g(n)+h(n),其中g(n)表示从起始搜索点到当前点的代价(通常用某结点在搜索树中的深度来表示),h(n)表示当前结点到目标结点的估值。实验数据和上文相同,在划定的区域(实验中使用的轨迹数据是经过指定起止点的)中使用Dijkstra算法和A*算法寻找最短路径,将实验数据分为10组,如:1 d、1~2 d、1~3 d、…、1~10 d,指定起始路段ID为51483701132、终止路段ID为51482708869,用户出行时间为高峰时段8:00-11:00,算法运行时间如图3所示。从图中可以看出本文提出的推荐算法相比于另外两种传统算法快得多。 图3 算法执行效率对比Fig.3 Comparison of algorithm execution efficiency 本文提出了一种基于频繁轨迹序列模式的路径推荐方法:基于历史轨迹数据构建路段轨迹序列数据库、路段索引表和频繁路段轨迹序列数据库,根据用户要求搜索得到候选路径集。利用所提出的频繁路径序列长短模式权重评估模型,基于各个候选路径中包含的频繁路径序列模式对其进行量化评估并进行排序,取出评估值前Top-n条路径为用户进行推荐。为了评估该路径推荐方法的合理性,本章最后设定了4个模拟场景,通过模拟案例对该路径推荐方法的分析结果表明,该推荐方法是具备合理性的,其为用户推荐的路径是符合大多数出租车驾驶员行车习惯的。同时实验研究证明,与传统的最短路径算法相比,该推荐算法推荐的路径在行驶时间、路径长度、平均速度、可靠性和稳定性方面表现更好,对比一般测试集更有优势,算法的运行速度更快。
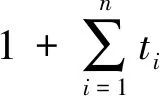
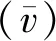
3 实验与分析
3.1 算法效果

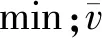
3.2 算法效率
4 结束语
