广义四元数群的幂图的电阻距离
2022-03-21潘向峰徐思奥李云翔
潘向峰,徐思奥,李云翔
安徽大学数学科学学院,安徽 合肥 230601
在该研究中,只考虑简单连通图。 对于一个简单图G=(V(G),E(G)),其中V(G)={v1,v2,…,vn}是G的顶点集,E(G)={e1,e2,…,en}是G的边集。 在图G中,两个顶点u,v之间的距离记为dG(u,v),被定义为两点之间的最短路的长度。 图G的直径D(G)是图中所有点对间的距离的最大值。 维纳指数(Wiener index) 是一个基于距离的拓扑指数,1947年由WIENER[1]提出并用于化学图论中,之后也被用于数学领域[2]。维纳指数定义为图G中所有点对之间的距离的和,即:
电网络理论中有许多的计算电阻距离的技术被提出,如串并联原理、星-三角变换[9]、消去原理[3]、星网变换[10]。各种计算电阻距离的公式也被推出,包括概率公式[11,12]、组合公式[13]、代数公式[3,5,13-17]等。一些特殊图类的电阻距离也被计算出来,如循环图[18]、轮图和扇图[19]、有限阿贝尔群上的凯莱图[20]、完全n部图[21]、环形网络[22]、两类硅酸盐网络[23]、汉诺塔图[24]、嵌套三角形网络[25]等。电阻距离的计算与一系列的问题相关,如图上随机游走[12]、覆盖花费[26]、点阵格林函数[27]等。
KERALEV和QUINN定义了半群S上的有向幂图[28]Pow(S),即一个有向图以S中所有元素为顶点,且对于S中任意不同两点u和v,若存在正整数m使得v=um,则有一条从u到v的弧。 后来,CHAKRABARTY等定义了半群S上的(无向)幂图[29]P(S) ,即一个(无向)图以S中所有元素为顶点,且对于S中任意不同两点u和v,如果存在正整数m使得v=um或u=vm,则u和v之间有一条边。也在[29]中证明了对任意的有限群Ω,幂图P(Ω)是一个完全图当且仅当Ω是一个循环群,且Ω的阶为1或pm,其中p是素数,m是正整数。
一个有限群Q4n称为广义四元数群,若Q4n=〈x,y|x2n=l,xn=y2,yxy-1=x-1〉,其中l是单位元,且n=2k,k∈N+。 笔者对广义四元数群的幂图的电阻距离、(度积、度和)基尔霍夫指数进行研究。
1 基本概念
若无特殊说明,图所对应的电网络指的是把图中每条边替换为单位电阻所得到的电网络。一个电网络也可以看作成一个权值图,其中每个边的权值表示边的电阻。对于图或电网络G,用rG(u,v)表示边e=(u,v)的电阻,用RG(u,v)表示顶点u和v之间的电阻距离。
对于图G中的两点x和y,当存在一条边e=(x,y)连接x和y时,称x和y是相邻的,并且x和y与e是相关联的。 点x的度,记为dG(x),是指G中与x相关联的边数。 图H是图G的子图,记为H⊆G,如果图H的顶点集和边集分别是图G的顶点集和边集的子集,即V(H)⊆V(G)且E(H)⊆E(G)。 对于2个连通图G和H,它们的联记为G∨H,其顶点集为V(G)∪V(H) 边集为E(G)∪E(H)∪{e=(x,y)|x∈V(G),y∈V(H)}。
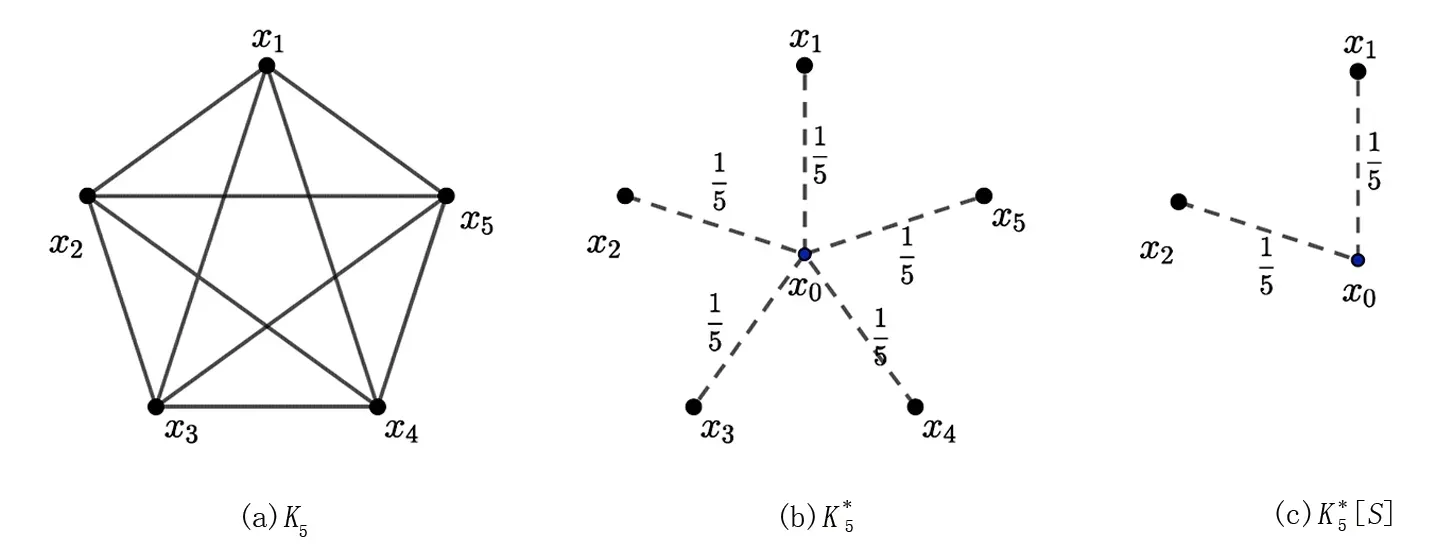
图1 5阶完全图K5及其等价电网络和应用消去原理后余下的网络其中S={x0,x1,x2}Fig.1 The complete graph K5 of order 5 and its equivalent network and the remaining network
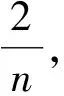
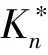
2 关于电网络的几个重要原理
1)串联原理。如果n个电阻值分别为r1,r2,…,rn的电阻串联,则可以用一个电阻值为R的电阻代替这n个串联的电阻,其中:
R=r1+r2+…+rn
(1)
2)并联原理。如果n个电阻值分别为r1,r2,…,rn的电阻并联,则可以用一个电阻值为R的电阻代替这n个并联的电阻,其中:
(2)
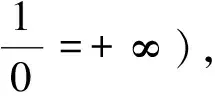
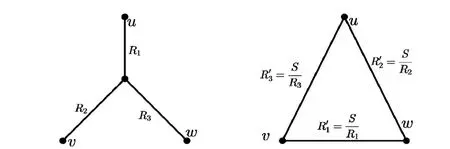
图2 星-三角变换(S=R1R2+R2R3+R3R1)Fig.2 Star-triangle transformation (S=R1R2+R2R3+R3R1)
3)星-三角变换[9]。一个星形电网络通过图 2 中的公式可以转换为一个等价的三角形电网络。
对于一个连通图G,如果移除一个顶点x后,使得图G不再连通,则点x是G的一个割点。一个不含割点的极大连通子图是图G的一个块。
4)消去原理[3]。设N是一个电网络且其基础图G是连通的,设B是G的一个块且含有G的一个割点x,将V(B)x中的顶点都从N中移除,得到的新的电网络记为M,则对于M中任意两个顶点u和v,都有RN(u,v)=RM(u,v)。
定义1设M,N是两个电网络且S⊆V(M)∩V(N),称M和N是S-等价的, 如果对于S中任意两点x和y,都有RM(x,y)=RN(x,y)。当S=V(M)∩V(N),即M和N是V(M)∩V(N)-等价时,称M和N是等价网络。
注1显然等价网络关系满足自反性和对称性。
5)星网变换[10]。在任意电网络N中,一个n+1个点的星可以替换为一个n点的网(即完全图)而不影响电网络中余下的部分,即新的电网络N*是N的一个等价网络。网中任意两点x和y之间的等价电阻如下:
其中:rx是点x和被移除的中心点之间的边的电阻。
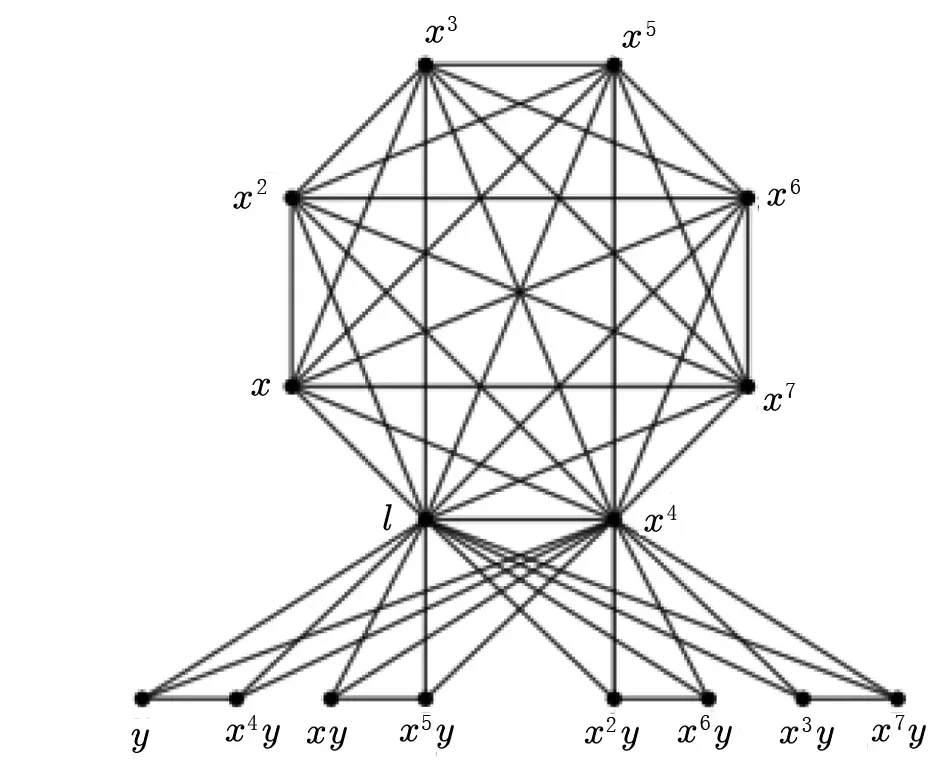
图3 广义四元数群Q16的幂图P(Q16)Fig.3 The power graph P(Q16) of generalized quaternion group Q16
注意到等价网络关系满足自反性,因此根据星网变换,可以得到了一个很重要的命题。
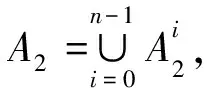
下面给出了P(Q4n)的具体结构。 当n=4时,P(Q16)如图3所示。
命题 2设P(Q4n)是广义四元数群Q4n的幂图。 则P(Q4n)=K2∨(K2n-2∪nK2)。
3 主要结果
3.1 广义四元数群的幂图P(Q4n)中任意两点之间的电阻距离
定理1设图P(Q4n)是广义四元数群Q4n的幂图,u和v是图P(Q4n)中任意不同的两点。A1,A2,A3如前所述,则u和v之间的电阻距离如下所示:
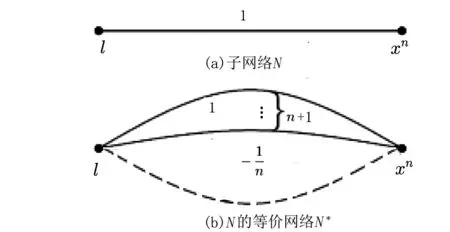
图4 子网络N和其等价网络N*Fig.4 Subnetwork N and its equivalent network N*
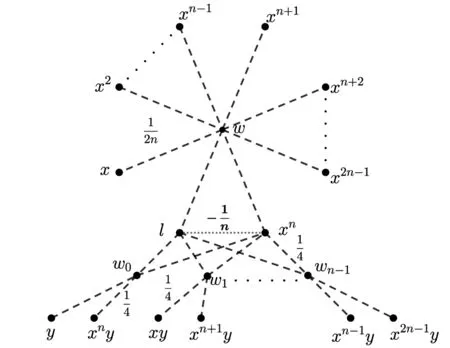
图5 P*(Q4n)的等价网络P(Q4n)Fig.5 The equivalent network P(Q4n) of P*(Q4n)
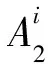
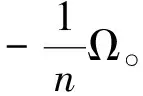
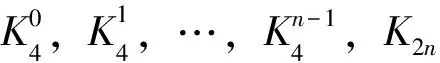
这里笔者仅对情形:
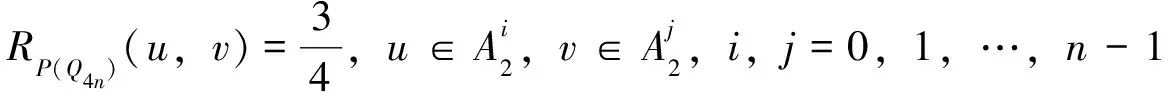
进行证明,其他情形类似可证。
不失一般性,设u=y,v=xy, 不难发现,顶点w,w0,w1,…,wn-1都是P(Q4n)的割点。首先,根据消去原理,可以得到P(Q4n)的等价网络如图6(a)所示;其次,根据串联和并联原理,把w,w2,w3,…,wn-1消去后,得到(Q4n), 如图6(b)所示; 第三步,对(Q4n)应用星-三角变换,把xn消去后,得到(Q4n),如图6(c)所示; 最后,根据串并联原理,有
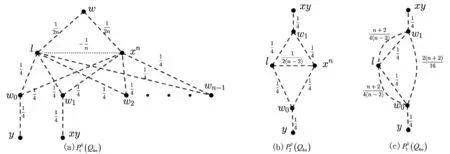
图6 P(Q4n)的等价网络(Q4n),(Q4n),(Q4n)Fig.6 The equivalent networks (Q4n),(Q4n),(Q4n) of P(Q4n)
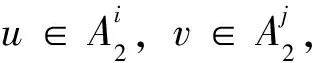
3.2 P(Q4n)的电阻直径
定理2设图P(Q4n)是广义四元数群Q4n的幂图,则:
3.3 P(Q4n)的基尔霍夫指数
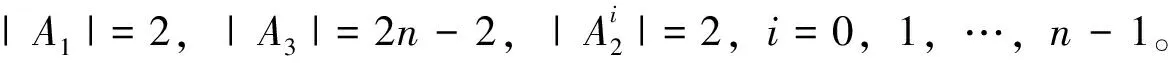
定理 3设图P(Q4n)是广义四元数群Q4n的幂图,则:
Kf(P(Q4n))=3n2+4n-4
证明
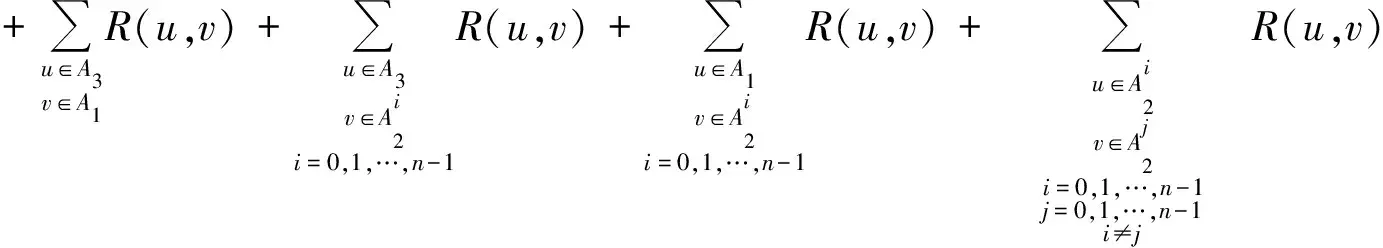
=3n2+4n-4
3.4 P(Q4n)的度积基尔霍夫指数
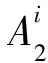
定理4设图P(Q4n)是广义四元数群Q4n的幂图,则:
Kf*(P(Q4n))=17n3+36n2-37n+11
证明
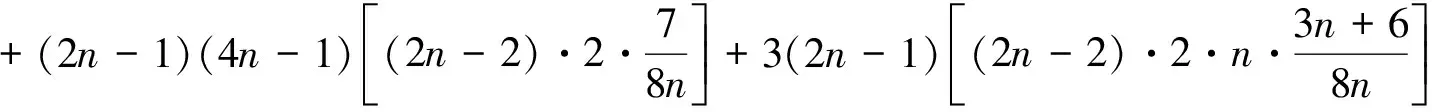
=17n3+36n2-37n+11
3.5 P(Q4n)的度和基尔霍夫指数
定理5设图P(Q4n)是广义四元数群Q4n的幂图,则:
Kf+(P(Q4n))=3n3+29n2-7n-7
证明
=3n3+29n2-7n-7
