复杂运输工况下堆码包装的疲劳寿命分析方法

曾台英，周龙炎，江海林

复杂运输工况下堆码包装的疲劳寿命分析方法

曾台英，周龙炎，江海林

（上海理工大学，上海 200093）

研究堆码产品的缓冲包装在连续复杂运输工况下的受到振动冲击后的疲劳损伤。采用Miner准则、Dirlik法和Steinberg三区间法，并结合Workbench和ncode疲劳分析模块建立2层堆码模型进行有限元仿真，通过不同工况的振动激励来模拟缓冲包装在复杂连续工况下的振动疲劳损伤并得出对应的疲劳结果云图和疲劳寿命云图。复杂工况下瓦楞外包装的疲劳寿命为9.26×109，最大节点处的损伤值为1.08×10−10，EVA内缓冲衬垫的疲劳寿命为1.882×1014，最大节点处的损伤值为5.313×10−15。堆码包装模型的易损点主要集中于内外缓冲包装的边角和楞边区域。通过Dirlik和Steinberg方法证明了缓冲件在经历16 h的复杂运输工况下的剩余寿命为2.6×104h和9.198×105h，利用Miner准则证明了缓冲包装结构对内部产品可以起到良好的保护作用。通过该种方法可以对堆码包装在复杂工况下进行可靠的疲劳寿命分析，并对堆码包装产品在进行多工况运输时的工况选择，以及结构上的优化设计提供了建议和参考思路。

堆码包装；复杂运输工况；频谱分析；疲劳寿命

伴随着电子商贸在全球范围内的不断扩张，单一的物流手段已经难以满足人们对于高速化的追求，现如今国际物流运输往往通过多式联运[1]来提高效率。多种运输载体的切换以及更复杂的载荷变化常常导致包装缓冲结构的疲劳损坏，从而引起了产品的破损，因此复杂物流环境下包装件的疲劳损伤，开始成为众多学者关注的问题。

陈志强等[2]研究了一种同时进行低气压环境与振动环境的实验方法，并研发一种低气压振动试验装置，对乳制品包装、充气包装、医疗包装的运输安全性进行了测试。杨平[3]对船舶在行驶过程中产生的随机振动从而导致的船舶疲劳问题进行了数学模型的建立，并利用实验进行了验证。张帆等[4]以多士炉包装为研究对象，利用SolidWorks建模并通过Workbench导入公路随机振动PSD曲线进行跌落和随机振动分析，并通过仿真结果对包装的脆弱部位进行了结构优化。王志伟等[5]通过实验和仿真研究对固定约束下包装件的响应特性进行了研究，说明了缓冲包装在整个运输过程的结构共振区域中起到了带通和放大的作用。李有堂[6]采用Miner损伤准则和Steinberg三区间法对合金管接头进行了随机振动振动分析，表明了接头在80 000 h内的飞行寿命安全可靠。

以上学者的研究主要集中于产品结构在单一工况下的随机振动疲劳分析和响应特性分析。在实际的国际贸易物流过程中，产品自生产线到客户手中往往会经历多种运输工况。鉴于上述，文中在考虑包装产品之间静载荷的影响下，构建堆码包装产品模型。通过Miner疲劳累积损伤理论、Dirlik寿命预测方法和Steinberg三区间法，结合有限元仿真的手段对堆码产品的缓冲包装在连续不同运输方式下产生的疲劳损伤进行分析，进而得出堆码包装件在复杂工况下的分析方法。

1 基于ncode的频域分析方法

1.1 Miner疲劳累积损伤理论

Miner线性疲劳累积损伤理论是分析疲劳的重要理论之一，在工程领域应用广泛。根据Miner理论，结构在不同应力水平下经受1,2,…,n次循环后的总损伤等于1时，结构才会发生破坏。当材料试样的加载历史由1,2,…,σ的的个不同的应力水平构成，每个应力水平下的疲劳寿命为1,2,…,N，各应力水平下的循环次数为1,2,…,n，则线性疲劳累积损伤准则可以表达为：

(1)

1.2 Dirlik寿命预测方法与Steinberg三区间法

基于产品—包装—运载体的整个运输包装系统，载体机械在服役过程中受到的载荷往往是不规则的，而在实际测试中，其得到的随机振动信号数据往往对应有时域和频域的处理方法。鉴于工程上频域处理的便捷性，一般通过研究功率谱密度的统计特性的数字特征[7]去实现频域分析。功率谱密度的关系式的数字特征可以用单边功率谱密度[8]表示为：

i

=0, 1, 2, 3,… (2)

式中：（）为应力谱密度；m为谱距。

对于整个运输包装系统在各工况下所经历的随机振动过程，在进行测试与计算过程中都假定为各态历经的、平稳的随机过程。本质上都是服从高斯概率分布的均匀随机场[9]。对于平稳随机过程的信号均值为，则系统在极短的单位间隔d内以正斜率的穿越发生率v为：

(3)

单位时间内的穿越率()为：

(4)

不规则因子2为：

(5)

随机振动的频域疲劳寿命分析方法众多，包括窄带近似法、α0.75法、Dirlik方法、Wirsching-Light方法等。程侃等[10]基于6种不同的频域疲劳计算模型对于汽车底盘的零件进行了损伤计算，结果显示了在公路运输工况下的Dirlik方法具有较高的准确性和适应性，Steinberg的三区间法简单高效，适用范围广。周凌波[11]运用多种频域方法求解某航空飞行器的加筋板件在航空运输中的疲劳寿命，结果显示Dirlik方法有着较小的误差。董磊等[12]根据铁路的试验标准设计仿真了辅助安装座，并使用Dirlik方法求解铁路运输中安装座的疲劳寿命。综上考虑到多式联运下的包装产品的载体的复杂性，文中将使用Dirlik寿命预测方法和Steinberg三区间法。

根据Dirlik公式有：

(6)

()为发生在时间内应力幅值为的循环次数：

(7)

Steinberg认为载体在振动环境下的Mises应力可以处理为3个应力区间：[−，+]、[−2～−1∪1～2]、[−3σ～−2∪2+3]，使用高斯分布和Miner疲劳损伤理论对概率分别为68.30%、27.10%、4.33%的3个区间进行简化，从而得出总损伤值为：

(8)

当临界总损伤值=1时，则可以求出振动时间为：

(9)

式中：1σ2σ3σ分别为材料在S-N曲线上应力水平1、2、3下对应的疲劳寿命。

1.3 ncode平均应力修正方法

载荷谱的平均应力对寿命有着较大的影响，在实际情况下受制于各方面条件的影响，很难得到多种不同的精确平均应力S-N曲线，故需要修正平均应力，将模型的实际应力状态按照相等寿命转换到材料测试的应力比状态[11]，公式为：

(10)

在不为−1时，修正公式为：

(11)

式中：a为材料在实际工况下的应力幅；m为材料在实际工况下的平均应力；为材料的极限拉伸强度；e为材料在−1情况下的应力。

1.4 ncode存活率设置

结构疲劳实验的获得的数据结果往往因为材料本身质量分布的不均匀性、尺寸大小的差异、实验载荷的差异以及影响实验的环境差异等因素而具有分散性，因此在实际情况下的存活率有偏差，需要对分散的寿命进行统计。ncode中存活率服从高斯分布：

(12)

式中：为样本方差；为样本均值

1.5 S-N曲线

利用ncode对瓦楞材料S-N曲线进行推测，根据表1参数结合文献[12]，求解瓦楞的向抗拉强度为：

(13)

式中：b为试样拉断时所承受的最大力；o为试样原始横截面积。计算求得瓦楞抗拉强度为1.53 MPa，EVA衬垫材料的抗拉强度为14.3 MPa。

2 双层堆码包装仿真分析

通过SolidWorks建立双层堆码包装的三维模型，在Workbench中对模型的材料属性、约束条件、接触关系进行赋予并完成网格划分。在分析过程中，通过模态分析以及谐响应分析获得频率响应函数（Frequency Response Funtion，FRF)，并在Ansys ncode designlife预定义的随机振动分析中，导入多种运输工况下的PSD功率谱结合疲劳寿命计算方法，对内外缓冲包装进行疲劳计算和分析[13]。

2.1 有限元模型的建立

利用SolidWorks软件对2层堆码包装产品进行三维实体建模。将固定约束下的堆码包装的螺栓简化为弹簧单元，并对模型中不影响实验过程和结果的倒角、曲面部分也进行适当的简化处理，从而降低模型在网格划分时的计算量。模型的实体包括5大部分：振动台、木板、瓦楞纸箱、EVA内衬、水泥块产品。材料参数[14]见表1。

对有限元模型进行接触设置，内部EVA缓冲材料与产品在轴向上设置为无摩擦接触，在平面采用不分离接触。缓冲材料与瓦楞包装接触设置为不分离接触，其他接触类型均设置为绑定接触。对瓦楞纸箱进行壳单元划分。对模型的底部施加固定约束，并将螺栓孔等效成弹簧单元。底座和木板使用六面体划分，其他使用四面体划分。整体模型的总计为93 108个节点数、52 843个单元数，模型网格划分后的整体见图1。

输入文献[14]的加速度功率谱，得到模型内部产品的第1共振频率为34.198，见图2。第1共振频率值与文献[14]实验结果误差仅为3.5%，验证了该模型的可靠性。

表1 材料特性

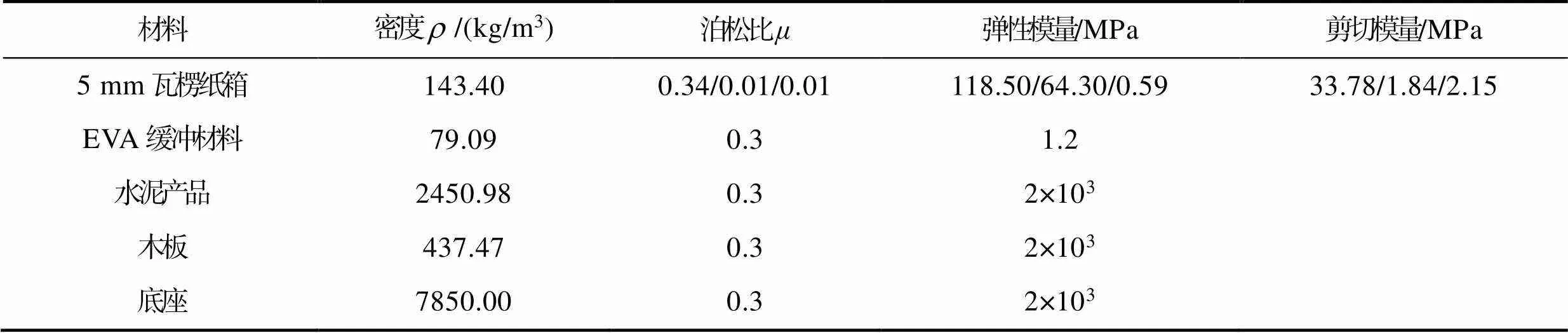
Tab.1 Material properties

注：0.34/0.01/0.01表示//方向的泊松比；118.50/64.30/0.59表示//方向的弹性模量；33.78/1.84/2.15表示//平面的剪切模量

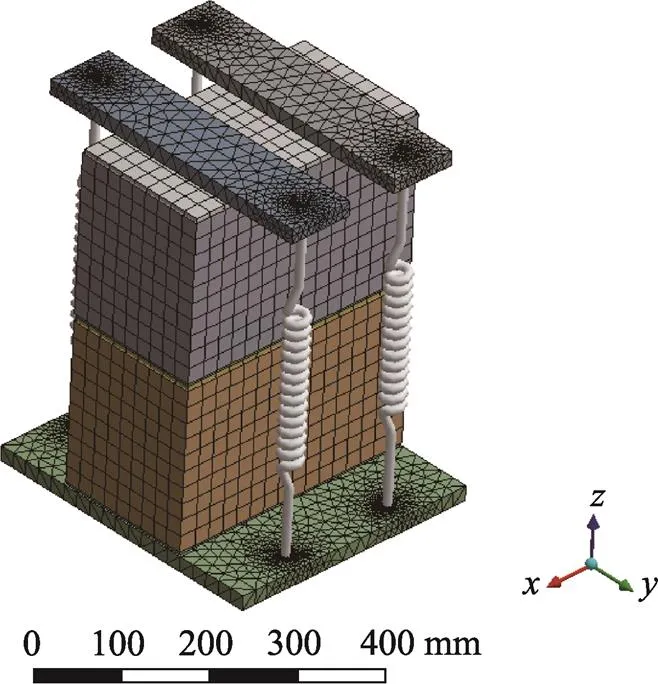
图1 双层堆码包装有限元网格划分

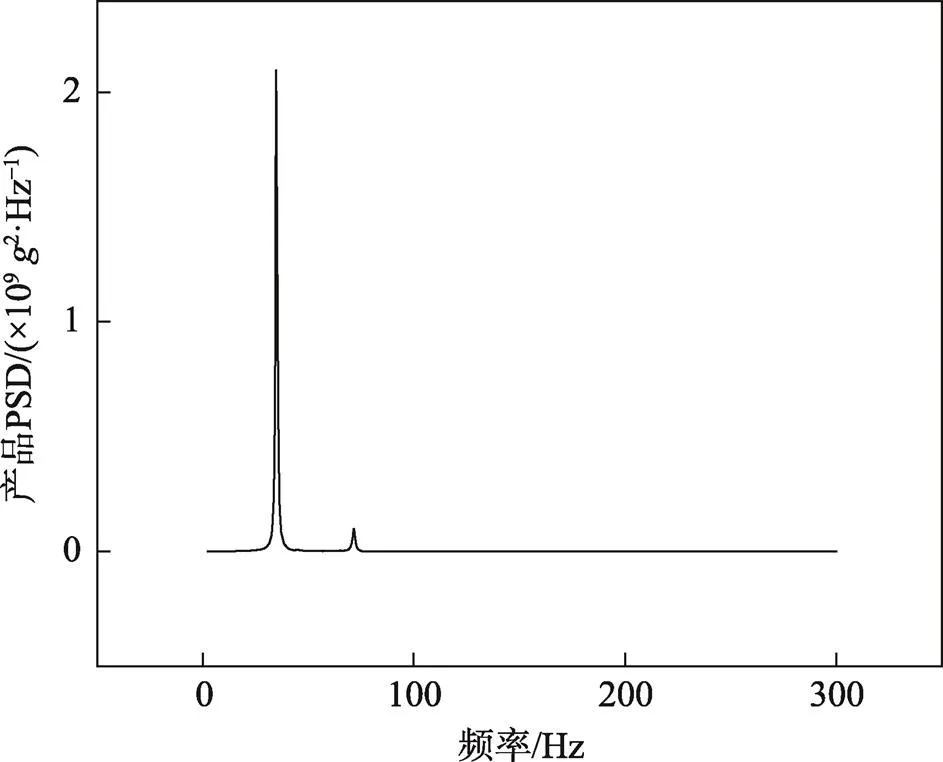
图2 产品的响应加速度功率谱

2.2 模态分析与谐响应分析

ncode通过模态分析和谐响应分析获得双层堆码包装模型的频率参数和频率响应函数，并获取包装结构的薄弱处[15]，从而进行随机振动疲劳分析。基于Workbench ncode designLife的模态分析要求在确定模态数量时，根据文献[11]计算的模态阶数的范围应为PSD激励最大频率的1.5倍。分析各运输载体的道路工况的频率范围，铁路、公路运输随机振动频率为1～200 Hz，低气压下的空运随机振动频率为2～300 Hz。设置模态阶数为6，前6阶模态分析结果见表2。

表2 前6阶模态振型特征

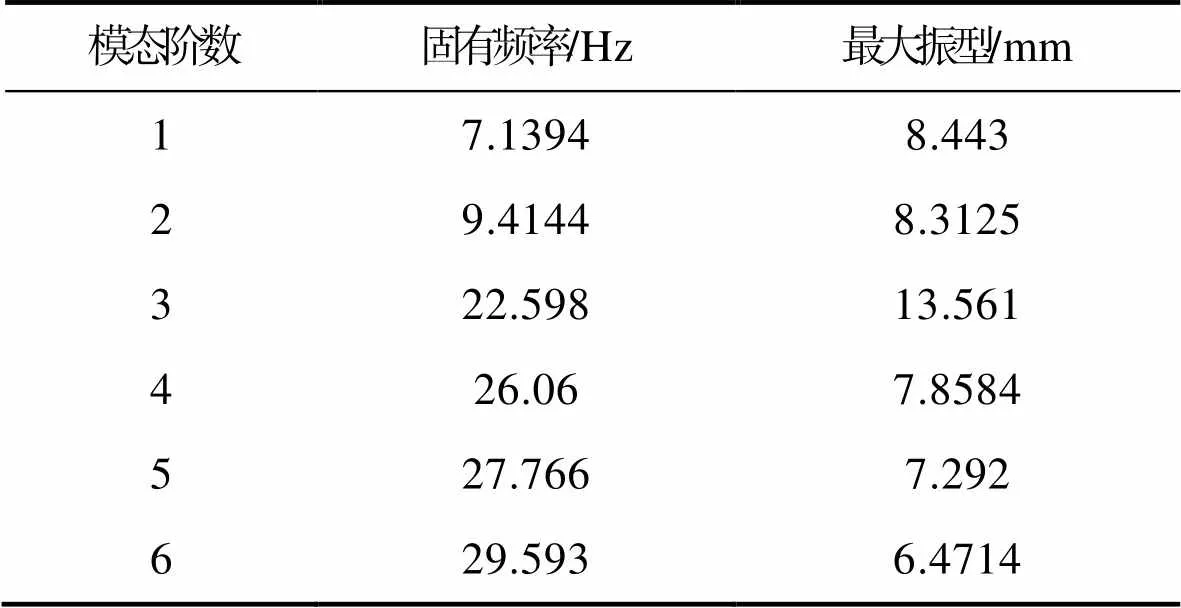
Tab.2 Characteristics of the first six modes

由前6阶模态振型特征可知，双层堆码包装的薄弱处主要集中于上层堆码件的顶部楞边区域以及下层堆码的中间区域，得到的前6阶固有频率都在200 Hz内，包装件易发生共振现象。上层堆码包装件的顶部区域承受了较大的受压变形，除此之外，底部包装件的内部受压变形较大。

谐响应分析共有2种方法：完全法（FULL）和模态叠加法（MSUP）。随机振动分析的目的在于生成频率响应函数，需要使用模态叠加法，因此文中将使用模态叠加法来求解随机振动的谐响应分析。定义频率为1～300 Hz，加速度信号为9800 mm/s2（轴）。

3 ncode随机振动疲劳寿命分析

3.1 载荷谱设置

对2层堆码包装件进行随机振动分析，将谐响应分析模块结果导入到Ansys ncode Designlife的随机振动分析模块，通过Vibration Load Provider提供PSD载荷的施加。基于当前的国际物流模式常常采用多式联运，多式联运有着融合仓储、运输的优势，可以及时将货物运送到目的地，从而使利润得到最大化，因此文中将采用多式联运的多运输工况。设置工况为：物流产品由A地经短途的公路运输1 h到达机场，经航空运输10 h后转由铁路运输5 h到达B地，不考虑整个运输过程中的产品清点、交接、装车时间。运输环境的激励模拟实验数据均采用美国材料与试验协会标准ASTM D—4169—14中严酷等级为Ⅱ的加速度功率谱[16]，见表3。

3.2 随机振动疲劳寿命求解

打开ncode模块，设置疲劳求解方法为Dirlik，应力修正方法根据式（8）结合实验模型分析使用Goodman法，Goodman适应于低韧性的材料，存活率根据式（10）设置为90。利用ncode对瓦楞材料S-N曲线进行推测，根据表1参数得出瓦楞的S-N曲线见图3。

结合之前Ansys Workbench的模态分析和谐响应分析获取的频率响应函数和传递函数，以及功率谱密度求解结构的疲劳寿命[17]，在随机振动载荷谱作用下，得到连续运输工况下的疲劳寿命循环数云图以及损伤值，见图4和图5。

表3 随机振动加速度功率谱

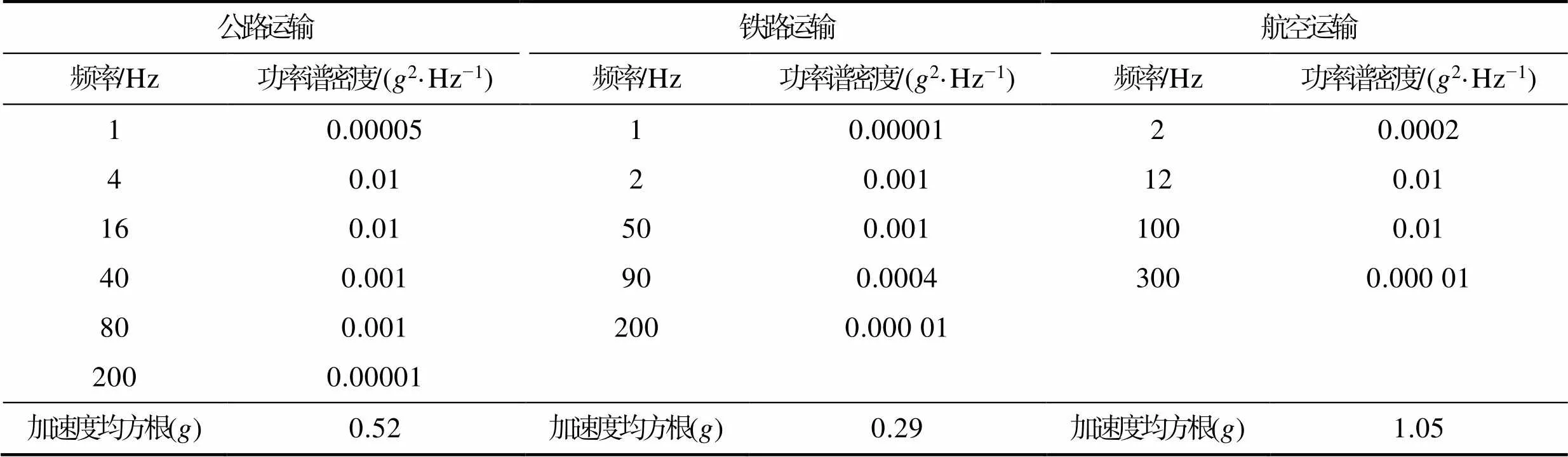
Tab.3 Acceleration PSDs of random vibration

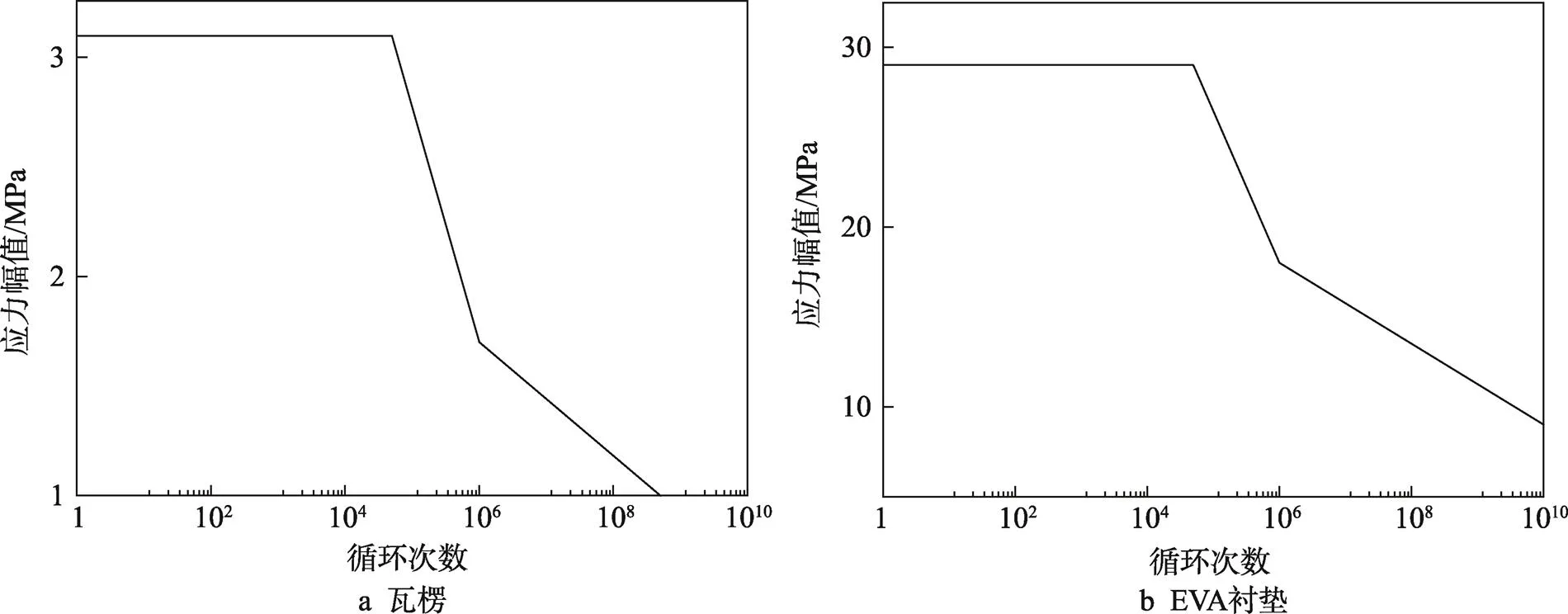
图3 内外缓冲包装材料的S-N曲线

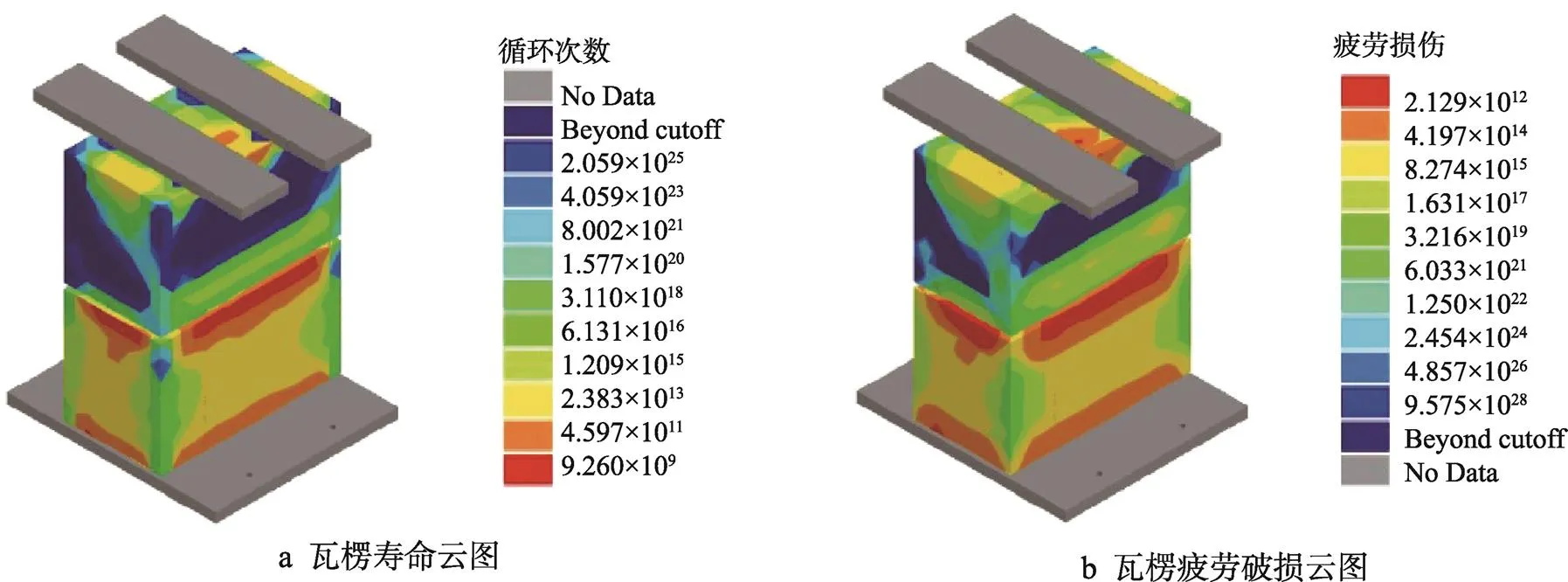
图4 瓦楞纸箱的疲劳损伤值与循环次数

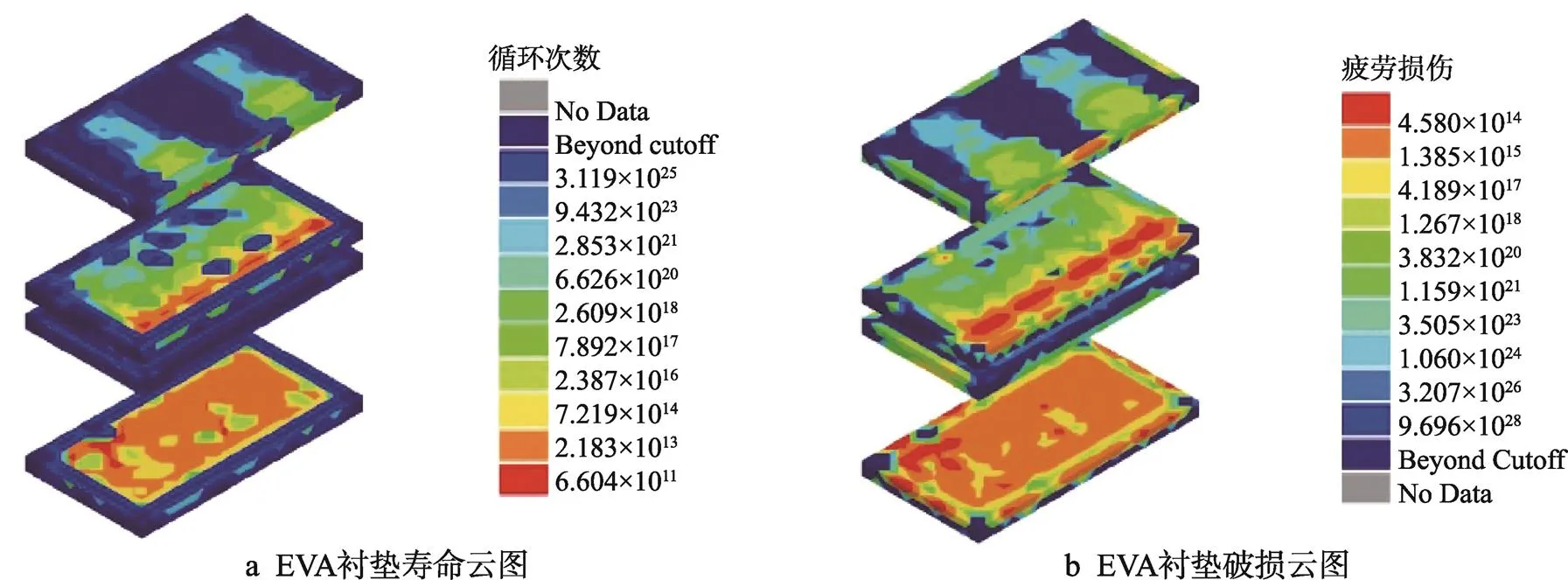
图5 EVA衬垫材料的疲劳损伤值与循环次数

由图4和表4可知，纸箱在节点73 830处产生了最大损伤值与最小寿命循环数。由图5和表5可以观察出，内部缓冲衬垫最大损伤节点为1232，损伤区域主要集中于包装件的边角和楞边区域，损伤区域的响应PSD曲线见图6。由于堆码包装件采用了固定约束的方式，整体包装件存在着连结耦合关系。考虑到固定约束方式对包装件产生的预压力和堆码件之间的抗压强度以及模态分析结果，可知底层堆码件在向上受到耦合力的影响均明显大于、方向的耦合力大小。实际运输中的下层堆码结构的加速度功率谱主要受1阶和2阶共振频率的共同控制，外缓冲包装在不同工况下的随机振动动压力功率主要受到1阶共振频率的影响，因此在对包装件结构进行改进时，不仅需要考虑到抗压强度，还需要考虑到包装件在边角和楞边区域的应力受力和共振情况。

不同运输工况下的随机振动均方根值反应了振动信号的振动强度强弱。由表3的信息可知，空运的均方根值远大于公路运输和铁路运输。空运是由于飞机起落时的振动，以及飞行时的振动情况，从而使得损伤值较大。根据运输载体实际振动强度下的分析可知，飞机在高空稳定飞行时产生的振动属于高频振动，相较于固有频率相对较低的普通包装件，飞机产生的高频振动传递小，受到的振动影响也小。铁路运输依赖于铁轨，由于铁轨之间的连接存在缝隙，往往振动存在周期性，并且铁路运输速度较慢，在现如今的物流环境下缺乏竞争力。公路运输方式最为广泛，它本身机动灵活并且可以实现短途运输。根据图6可知，公路运输振动频率较低时的功率谱波动很大，考虑到堆码包装易受到低频共振的影响，应重视公路运输时包装件的结构优化，因此复杂运输工况下的产品包装往往比单一运输下的产品包装的损伤值更大，而共振的情况的发生率更小。

表4 各工况下瓦楞纸箱的疲劳损伤与寿命值

Tab.4 Fatigue damage and life value of corrugated carton under different working conditions

表5 各工况下EVA衬垫的疲劳损伤与寿命值

Tab.5 Fatigue damage and life value of EVA liner under different working conditions

除开包装件自身结构的因素外，包装的损伤还取决于道路的严酷等级、环境温湿度、人为暴力搬运等多种因素。这些因素使得包装件的受到的随机耦合激励增大，从而对内外的缓冲包装甚至内部产品产生更大的损伤。由表4和表5可知，瓦楞与EVA衬垫的最小寿命时长约为3年和105年。根据瓦楞的正常使用GB/T 6544—2008中瓦楞出厂的储藏期不超过半年，并且使用期间应保持通风、远离明火等，因此正常的保存情况下，瓦楞和EVA可以满足正常的使用要求。

3.3 疲劳寿命评估

总运输时长为16 h，短途的公路运输时长为1 h，航空运输时长为10 h，铁路运输时长为5 h，即1=3.6×103s、2=3.6×104s、3=1.8×104s。公路、铁路振动频率为1～200 Hz，空运振动频率为2～300 Hz。根据相应工况的输入频率可得公路和铁路的平均频率V为99次，空运的平均频率V为149次。各类运输方式的各区间应力值见表6。

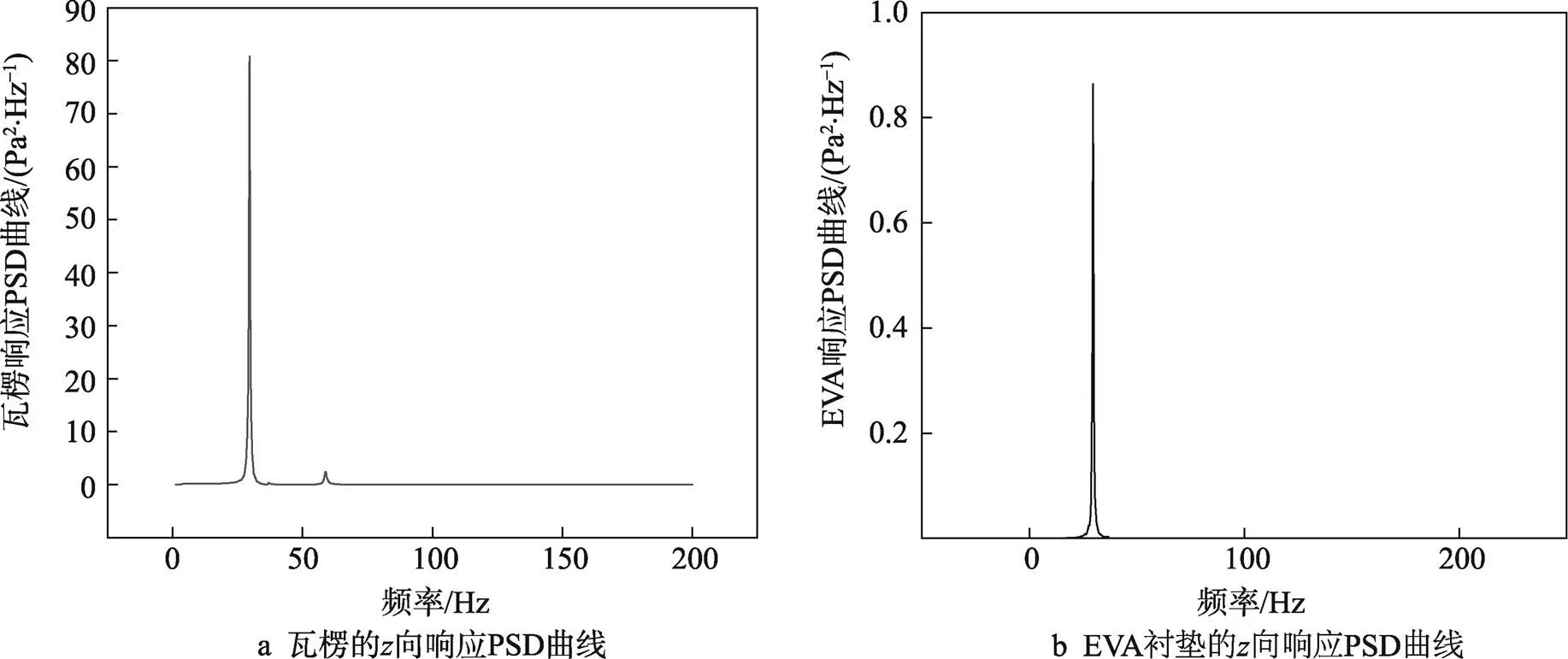
图6 内外缓冲包装z向响应PSD曲线

表6 各工况下内外缓冲包装的应力值

Tab.6 Stress value of internal and external cushion packaging under different working conditions

根据表6和图3数据可以得出1下公路的瓦楞外缓冲包装的总循环次数1σ≈5×108，2下的总循环次数1σ≈5×1083下的总循环次数1σ≈5×108，EVA缓冲衬垫1下的总循环次数1σ≈+∞2下的总循环次数1σ≈+∞3下的总循环次数1σ≈+∞，根据式（8）可得：

1σ= 0.683aT1=2.43×105

n= 0.2718aT1=9.68×104

n= 0.0428aT11.52×104

计算瓦楞外缓冲包装在经历公路运输后产生的损伤值≈7.1×10−4。同理可得出铁路运输的疲劳损伤值约为3.5×10−3，空运的疲劳损伤值约为1.9×10−2。EVA内缓冲衬垫的公路运输的损伤值约为0，铁路运输的损伤值约为0，空运的损伤值约为0。根据式（9）计算瓦楞的振动时长为1.4×103s，EVA的振动时长约为0。

多式联运下的瓦楞包装的总损伤值约为0.023，EVA内缓冲衬垫的总损伤值约为0。根据Miner线性疲劳累积损伤当结构在不同应力水平下经受1,2, …,n次循环后的总损伤等于1时，结构才会发生破坏。瓦楞外缓冲包装和EVA内缓冲衬垫在经历连续多工况下的总损伤值之和都远小于1，并且两者的剩余寿命约为2.6×104h和9.198×105h。说明堆码包装件的瓦楞纸箱与EVA缓冲衬垫可以很好地适应运输疲劳要求，具有较大的寿命富裕度。

4 结语

文中通过SolidWorks进行双层堆码包装的实际建模，并利用Workbench和ncode软件结合了功率谱密度、Miner疲劳累积准则、Dirlik疲劳寿命预测方法、Steinberg三区间法对模型在不同运输工况下的疲劳损伤进行了分析。结合模态分析和随机振动疲劳分析的结果，得出了复杂运输工况下包装件的损伤点所在位置主要集中于边角以及楞边区域。建立了实际的复杂运输工况，并进行寿命计算。通过疲劳寿命预测方法和Miner疲劳累积准则进行了分析，进而提出了一种基于多工况下的疲劳寿命分析方法，为堆码包装产品经历复杂工况运输时的工况选择和结构优化提供了参考意见。

[1] 李万里. 探究国际物流管理与多种运输方式的选择和应用[J]. 全国流通经济, 2019(8): 18-19.

LI Wan-li. Explore the Choice and Application of International Logistics Management and Various Modes of Transportation[J]. China Circulation Economy, 2019(8): 18-19.

[2] 陈志强, 尹兴, 魏娜, 等. 运输包装件低气压振动模拟试验方法[J]. 包装工程, 2021, 42(5): 157-162.

CHEN Zhi-qiang, YIN Xing, WEI Na, et al. Simulation Test Method for Low Pressure Vibration of Transport Package[J]. Packaging Engineering, 2021, 42(5): 157-162.

[3] 杨平. 船舶寿命估计的数学模型构建及实验验证[J]. 舰船科学技术, 2020, 42(20): 16-18.

YANG Ping. Mathematical Model Construction and Experimental Verification of Ship Life Estimation[J]. Ship Science and Technology, 2020, 42(20): 16-18.

[4] 张帆, 汤婧雅, 朱友林. 基于ANSYS Workbench的多士炉包装设计与仿真分析[J]. 数字印刷, 2020(1): 29-37.

ZHANG Fan, TANG Jing-ya, ZHU You-lin.Packaging Design and Simulation Analysis of Toaster Based on ANSYS Workbench[J]. Digital Printing, 2020(1): 29-37.

[5] 王志伟, 林深伟. 随机振动下产品包装件动态响应的实验研究和有限元分析[J]. 振动与冲击, 2017, 36(13): 223-229.

WANG Zhi-wei, LIN Shen-wei. Tests and FE Analysis for Dynamic Responses of Packaged Products under Random Vibration Environment[J]. Journal of Vibration and Shock, 2017, 36(13): 223-229.

[6] 李有堂, 王标. 随机振动下镍钛形状记忆合金管接头的疲劳寿命分析[J]. 兰州理工大学学报, 2020, 46(3): 155-159.

LI You-tang, WANG Biao. Fatigue Life Analysis of Ni-Ti Shape Memory Alloy Pipe Joints under Random Vibration[J]. Journal of Lanzhou University of Technology, 2020, 46(3): 155-159.

[7] 王永德, 王军. 随机信号分析基础[M]. 5版. 北京: 电子工业出版社, 2020: 60-70.

WANG Yong-de, WANG Jun. Fundamentals of Random Signal Analysis[M]. Beijing: Publishing House of Electronics industry, 2020: 60-70.

[8] KIM H G, KIM G C, JI W, et al. Random Vibration Fatigue Analysis of a Multi-Material Battery Pack Structure for an Electric Vehicle[J]. Functional Composites and Structures, 2021, 3(2): 025006.

[9] 罗文韬. 钢桥汽车振动问题浅析[J]. 黑龙江科技信息, 2013(15): 39.

LUO Wen-tao. Analysis on Vibration of Steel Bridge Vehicle[J]. Heilongjiang Science and Technology Information, 2013(15): 39.

[10] 程侃, 赵礼辉, 刘斌, 等. 频域疲劳寿命预测方法对比与分析[J]. 农业装备与车辆工程, 2018, 56(9): 1-5.

CHENG Kan, ZHAO Li-hui, LIU Bin, et al. Comparison and Analysis on Fatigue Life Prediction Methods in Frequency Domain[J]. Agricultural Equipment & Vehicle Engineering, 2018, 56(9): 1-5.

[11] 周凌波. 航空典型结构件的随机振动疲劳寿命分析[D]. 南京: 南京航空航天大学, 2014: 20-26.

ZHOU Ling-bo. Random Vibration Fatigue Life Analysis of Aircraft Typical Structures[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014: 20-26.

[12] 董磊, 付德龙, 安靖宇, 等. 随机振动疲劳分析方法在高速铁路车辆上的应用[J]. 机车车辆工艺, 2021(1): 5-8.

DONG Lei, FU De-long, AN Jing-yu, et al. Application of Random Vibration Fatigue Analytical Method in High Speed Railway Vehicles[J]. Locomotive & Rolling Stock Technology, 2021(1): 5-8.

[13] 何稣昇. ANSYS ncode DesignLife疲劳寿命分析基础与实例教程[M]. 北京: 人民邮电出版社, 2020: 213-227.

HE Su-sheng. Fundamentals and Examples of ANSYS Ncode DesignLife Fatigue Life Analysis[M]. Beijing: posts＆Telecom Press, 2020: 213-227.

[14] 骆光林. 包装材料学[M]. 2版. 北京: 印刷工业出版社, 2011: 87-88.

LUO Guang-lin. Packaging Material Science[M]. Beijing: Printing Industry Press, 2011: 87-88.

[15] WU Ning-qiang, WANG Yan-xia, WEI Ming-huai. Fatigue life Analysis of Driving Shaft of Conveyor System Based on nCode Design-Life[J]. International Core Journal of Engineering, 2019, 5(9): 1-5.

[16] GB/T 4857.23—2012, 包装运输包装件基本试验第23部分: 随机振动试验方法[S].

GB/T 4857.23—2012, Packaging-Basic Tests for Transport Packages Part 23: Random Vibration Test Method[S].

[17] USIU S, BAYRAKTAR M, DEMIR C, et al. Innovative Computational Modal Analysis of a Marine Propeller[J]. Applied Ocean Research, 2021, 113: 102767.

Fatigue Life Analysis Method of Stacked Products under Complex Transportation Conditions

ZENG Tai-ying, ZHOU Long-yan, JIANG Hai-lin

(University of Shanghai for Science and Technology, Shanghai 200093, China)

The work aims to study the fatigue damage of cushion packaging of stacked products after vibration and shock under continuous complex transportation conditions. Miner’s rule, Dirlik's method and Steinberg’s three-interval method, combined with Workbench and ncode fatigue analysis module, were used to build a two-layer stacked packaging model for finite element simulation. The vibration fatigue damage of cushion packaging under complex continuous working conditions was simulated by vibration excitation under different working conditions and the corresponding fatigue result and fatigue life cloud diagram were obtained. Under complex working conditions, the fatigue life of corrugated packaging was 9.26×109and the damage value at the maximum node was 1.08×10−10. The fatigue life of EVA internal cushion liner was 1.882×1014and the damage value at the maximum node was 5.313×10−15. The vulnerable points of stacked packaging model were mainly concentrated at the corners and edges of internal and external cushion packaging. Dirlik and Steinberg methods were used to prove that the residual life of the cushion was 2.6×104h and 9.198×105h under the complex transportation condition for 16 h. The Miner’s rule was used to prove that the cushion packaging structure could play a good role in protecting the internal products. By this method, the fatigue life of stacked packaging can be analyzed reliably under complex working conditions, and some suggestions and reference ideas are provided for the selection of working conditions and the optimal design of structure of stacked packaging products during transportation under multiple working conditions.

stacked packaging; complex transportation condition; spectral analysis; fatigue life

TB484.1；TB484.3

A

1001-3563(2022)05-0159-08

10.19554/j.cnki.1001-3563.2022.05.022

2021-08-12

高水平大学科建设医工交叉创新项目（10-20-309-402）

曾台英（1978—），女，上海理工大学讲师、硕导，主要研究方向为包装运输动力学。