基于相对坐标的空空导弹截获概率计算模型

李 斌，强艳辉

(1 中国空空导弹研究院，河南 洛阳 471009；2 海军装备研究院，北京 100161)

0 引言

捷联惯导+双向数据链修正+末制导是现代中远距空空导弹普遍采用的复合制导体制，在中末制导交接班时需要完成导引头交接班[1-3]和弹道交接班[4-6]，导引头交接班是根据平台目标指示信息在设计条件下完成导引头截获并稳定跟踪目标，弹道交接班是实现中制导和末制导弹道平滑过渡。中末制导导引头交接班时导弹对目标的截获概率是导弹总体性能设计的一项重要指标。工程上可采用蒙特卡洛法[7]或方差法[8]计算截获概率，蒙特卡洛法需要对典型弹道进行多次解算并取统计值，计算量大且效率不高。为提高计算截获概率效率，文献[1]将各种测量误差等效转换为目标指示误差，建立了在一次弹道解算中得到该弹道的截获概率模型，并对主要误差源进行了影响分析。文献[2]将文献[1]方法扩展到红外型空空导弹截获概率计算，同时考虑了影响红外成像导引头图像处理过程目标识别的影响，文献[3]借鉴文献[1]的等效转换思路，提出将各种误差转换到导弹位置散布和偏差上，并推导了截获概率计算公式。

采用误差等效转换方法建立的截获概率模型可用于研究各误差源对截获概率的影响。文献[1]指出对截获概率影响较大的是对准误差和机载雷达测量误差，其放大因子与导弹截获距离成反比。现代战机隐身性能大幅提升，导弹对隐身目标探测截获距离明显下降，如战斗机的RCS降低20倍，则导弹探测截获距离约下降一半，对准误差和雷达测角误差的影响也放大了一倍，从而降低了导弹对目标的截获概率。工程实际中，继续减小对准误差和机载雷达测量误差的费效比很高，迫切需要新的方法提高中远距空空导弹在中末制导交接班时的截获概率。

在地空导弹武器系统中，采用相对坐标计算中末制导交接班时的目标指示误差，能提高导弹的截获概率[9-10]，公开资料表明，对于空空导弹武器系统采用相对坐标计算目标指示误差的研究非常少，文献[11-12]采用相对坐标计算了空空导弹的截获概率，但都未给出目标指示误差的计算方法。文中采用相对坐标推导了目标指示误差计算公式，并分析了主要误差源，与文献[1]绝对坐标方法进行了对比，结果表明，采用相对坐标的计算模型可显著提高中远距空空导弹在中末制导交接班时的目标截获概率。

1 截获概率计算模型

对于空空导弹，其完成对目标的截获需同时满足角度截获和距离截获两个条件，角度截获要求导引头光轴指向与实际弹目连线的夹角小于导引头半视场角，距离截获要求弹目距离不大于导引头稳定截获距离。文中只考虑角度截获，且假设导引头对落入视场目标的识别概率为1。

在中末制导交接班时，导弹导引头根据目标指示信息指向目标，但由于测量等误差因素，导引头光轴指向目标附近区域而偏离真实目标，即为目标指示误差。目标指示误差是均值为m，方差为σ的随机变量，如图1所示。图中Δφy、Δφz分别为方位角和高低角指向误差，点T为导引头视场中心，d为导引头半视场，点O为目标指示散布中心，点O与点T之间距离为目标指示误差均值m。目标指示以高概率落入以点O为圆心、3σ为半径的圆内，圆O和圆T重叠部分即为目标落入导引头视场概率，在假设识别概率为1时，落入概率即为截获概率。

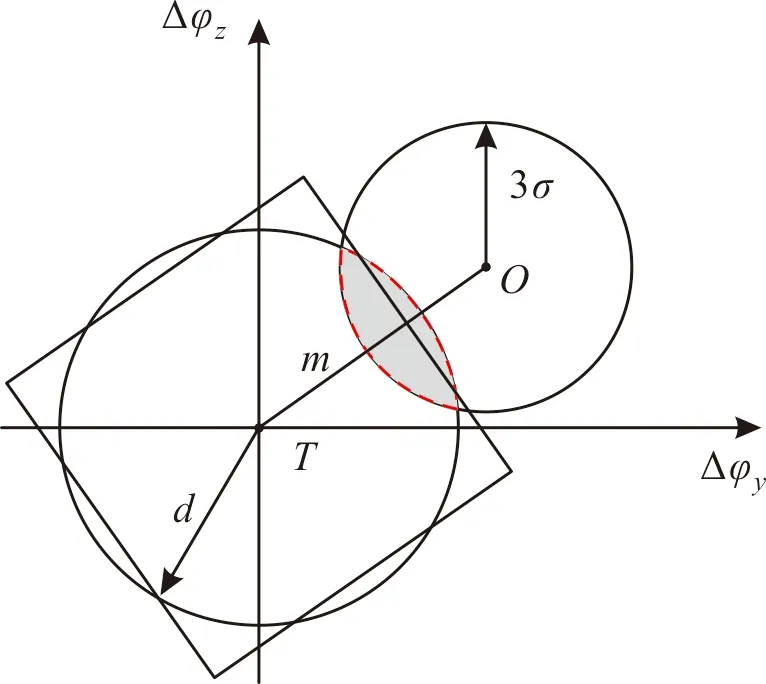
图1 落入概率示意图

落入概率P0计算公式为：

P0=(2F(U1)-1)·(F(U2)-F(U3))

(1)

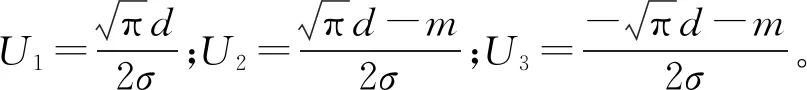
(2)

在不考虑目标识别概率时，P0即为截获概率。截获概率在实际工程计算中还要考虑累积过程[1-2,13]。

2 目标指示误差源分析

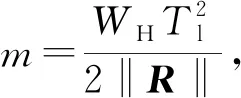
采用捷联惯导/卫星组合导航提高导弹位置和速度精度，可有效减小导弹中末制导交接班时导引头的目标指示误差，同时考虑到随着弹载加计和陀螺精度的不断提高，导弹加计和陀螺测量误差对目标指示误差影响已经很小，可以忽略[1,14]。

下面主要分析对准误差和测角误差对目标指示误差的放大效应影响。

2.1 对准误差

在导弹发射前，载机主惯导与导弹子惯导要进行对准，主子惯导之间存在对准误差，包括姿态、速度和位置误差，由于速度和位置误差很小，忽略二者影响。子惯导中弹目矢量与主惯导中弹目矢量夹角即为对准误差，文献[1]给出对准误差产生的目标指示误差SB计算公式如下：

(3)

式中：Φ为对准误差矢量；R为弹目相对位置向量，在交接班时R数值等于导引头探测距离；RW为不考虑初始速度，仅由导弹加速度传感器测量值的积分得到的飞行距离。

2.2 机载雷达测量误差

文献[1]给出机载雷达测量误差产生的目标指示误差SR计算公式，简化后如下：

(4)

式中：SYY为机载雷达测角误差Φra的方差；Sdd为机载雷达测距误差Φrd的方差；Svv为机载雷达测速误差Φrv的方差；RH为载机与目标的距离矢量；α为R和RH之间的夹角。

测距误差与导引头探测距离相比通常很小，测速误差和数据链传输周期也很小，因此忽略机载雷达测距误差和测速误差对目标指示误差的影响。

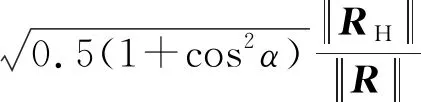
3 基于相对坐标的截获概率计算模型

基于相对坐标的目标指示误差计算模型是在机载雷达同时测量导弹与目标的位置、速度和角度信息时，利用机目矢量RFT、机弹矢量RFM和其夹角θ可确定导弹与目标矢量方向，即目标指向。如图2所示，点F、点M和点T分别表示载机、导弹和目标。

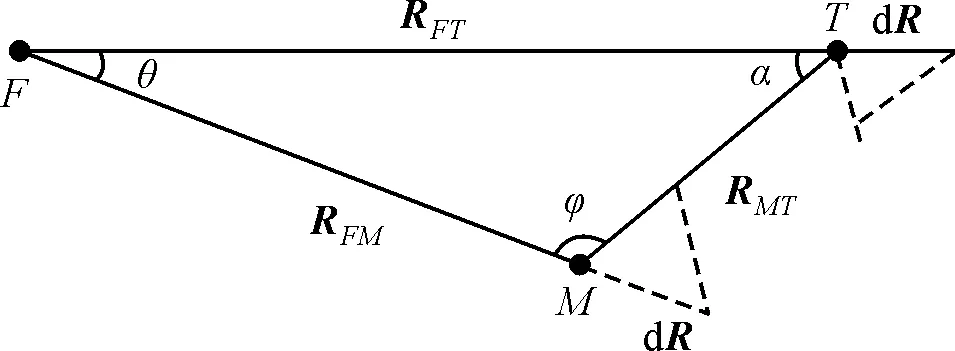
图2 机弹目相对位置示意图

基于相对坐标的主要误差源包括量机载雷达测相对角度误差、测角误差、测速误差、测距误差和目标机动误差。

(5)

导引头光轴空间指向可表示为：

(6)

对式(6)进行全微分，可得相对坐标引起的导引头光轴空间指向误差为：

(7)

式中：

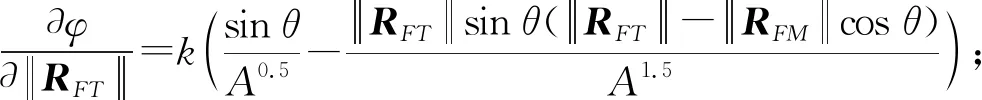
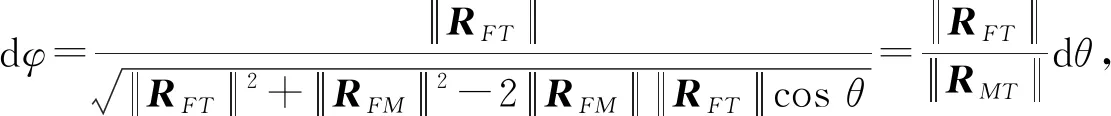
综上所述，基于相对坐标的目标指示误差可由均值和上述随机误差的方差计算。

采用相对坐标计算目标指示误差，导引头利用机载雷达测量目标和导弹相对位置，解算导引头光轴指向，与导弹捷联惯导计算的位置精度无关，因此目标指示误差与对准误差无关，同时未放大机载雷达测角误差。采用相对坐标新引入了测量相对角误差，且该误差要被放大，但由于测量相对角误差可消除机载雷达系统误差，仅余机载雷达随机误差，测量相对角误差引起的目标指示误差小于测量绝对坐标测角误差引起的目标指示误差。

采用相对坐标计算中末制导交接班时的目标指向，可有效抑制对准误差和测角误差对目标指示误差的影响，同时使随导弹飞行距离放大的误差源只剩下测相对角误差，且相对角误差精度高于测角误差精度。因此采用相对坐标可以提高中末制导交接班时的目标指示误差精度，提高目标的截获概率。

4 对比仿真分析

取迎头发射距离150 km典型弹道中末制导交接班时参数：A-极距离为85 km，对典型三代机(RCS=2 m2)导引头探测距离为20 km[10]，导弹纯惯导飞行65 km，机弹距离为65 km，α=15°，θ=4.5°，数据链更新周期Tl为1 s，目标机动为9g。采用文中方法和文献[1]方法计算的目标指示误差数值分别为0.7°，1.79°。其误差源及取值见表1。其中，输入项为理论误差(1σ)；对准误差为0.3°；测角误差为0.3°；目标测速误差为30 m/s；导弹测速误差为60 m/s；目标测距误差为60 m；导弹测距误差为120 m；测相对角误差为0.15°；机动误差为0.13°；弹载加速度计误差为20 m；弹载陀螺误差为0.1°。

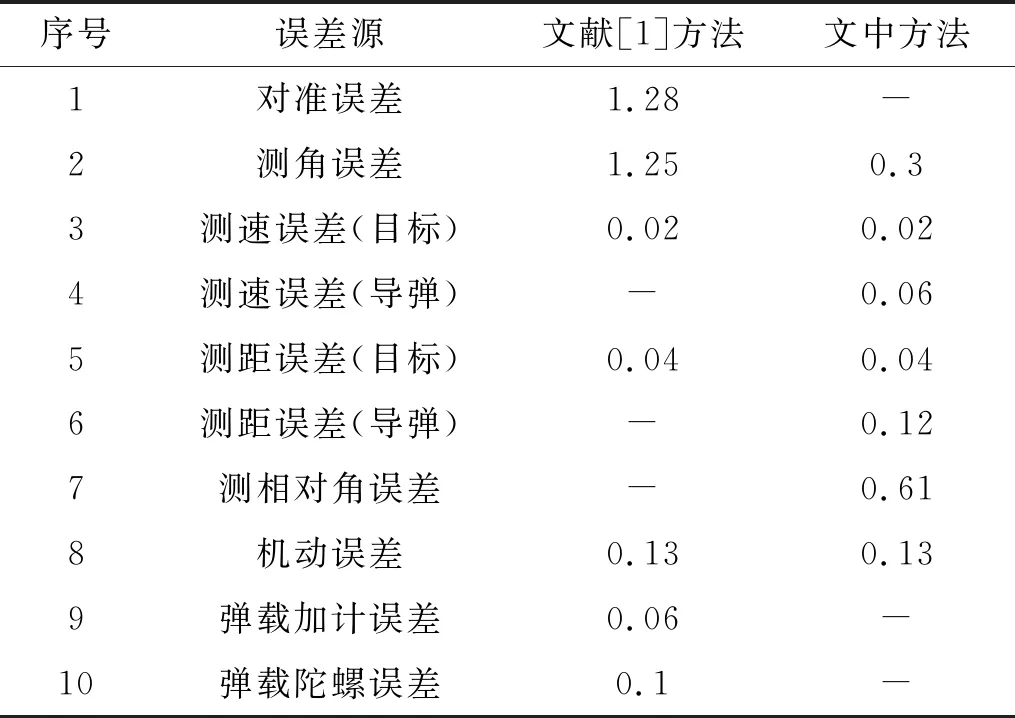
表1 目标指示误差 单位：(°)

根据表1计算的中末制导交接班时目标的截获概率对比见表2。

表2 对三代机目标的截获概率

取迎头发射距离150 km典型弹道中末制导交接班时参数：A-极距离为80 km，对隐形三代机(RCS=0.1 m2)导引头探测距离为9.5 km，导弹纯惯导飞行70 km，机弹距离为70 km，α=17°，θ=2.5°，数据链更新周期Tl为1 s，目标机动为9g。目标机动引起的目标指示误差均值m=0.25°。采用文献[1]方法计算的目标指示误差为3.36°，采用文中方法计算的目标指示误差为1.21°。截获概率对比见表3。

表3 对三代机目标的截获概率对比

从表2和表3可以看出，采用相对坐标的计算模型截获概率明显提高。在中远距空空导弹攻击隐身目标时，由于导引头探测截获距离大幅降低，采用绝对坐标得到的目标截获概率显著降低，即使在将导引头视场提高到±6°时，其对应的目标截获概率仍不具备工程意义。从提高目标截获概率角度，导引头视场越大越好，但大视场会导致背景噪声增多，给导引头稳定截获和抗干扰带来不利影响[15-16]。工程上一般采用导引头光轴扫描的方法，以较小的瞬时视场获得尽可能大的搜索视场，搜索策略、周期以及目标在视场中驻留时间等都会影响截获概率。因此在攻击隐身目标时，采用扩大导引头视场不能无限提高中末制导交接班时的目标截获概率。

采用相对坐标计算目标指示误差，不仅可以提高导弹对目标的截获概率，可以增大导弹的A-极距离，间接提高了载机平台的生存能力。

5 结论

中远距空空导弹攻击隐身目标时，攻击距离增大和探测距离降低双重加剧了对准误差和测角误差对目标指示误差的放大效应，在攻击距离不变时会显著降低目标截获概率。为提高中远距空空导弹攻击隐身目标中末制导交接班时的截获概率，文中采用了相对坐标计算目标指示误差，推导了空空导弹武器系统采用相对坐标计算目标指示误差的计算公式。与采用绝对坐标计算目标指示误差相比，所提出的方法消除了对准误差和测角误差引起的放大效应，增加的测相对角误差虽被放大但其测量精度高，综合提高了目标指示误差的精度，提高了目标截获概率。更具备工程意义的是，采用相对坐标提高目标截获概率的同时，也提高了导弹的A-极距离，进而提高了载机平台的生存能力。