面向非正交多址接入无人机系统的能效优化算法

陈德全

(重庆幼儿师范高等专科学校儿童智能科学与技术系，重庆 404047)

0 引言

地震、洪水等自然灾害对地面通信系统有毁灭性影响。一旦发生灾害，灾区居民的通信需求迅速增加，使通信负荷急剧增长。同时，灾害可能破坏了原有通信设备，降低了对灾区居民的服务质量。然而，保持通信畅通是开展灾区救援工作的前提条件[1]。由于维修或者重建通信系统耗时且不易操作，利用无人机组建应急通信系统是行之有效的方法。与传统的固定基站相比，利用无人机作为空中基站可极大地提高灾区居民(地面用户)的通信质量[2]。

此外，非正交多址接入(non-orthogonal multiple access, NOMA)技术是5G无线通信的重要技术，其允许多个用户以不同功率将多个信息流在同频域信道上传输[3]，即NOMA技术能够在相同的资源上为多个用户提供无线通信业务。NOMA的基本思想为：发送端采用正交传输数据，主动引入干扰信息；在接收端通过串行干扰删除(successive interference cancellation, SIC)[4]技术进行解调，进而提高频谱利用率。

研究人员将NOMA应用于无人机基站通信网络[5-11]，提高通信服务质量，文献[5]基于功率域的NOMA网络模型，提出了基于用户配对的能效无人机部署策略；文献[6]分析了功率分配和最大化下行链路速率问题。

然而，这些研究工作并没有在满足用户端的信号质量、用户向无人机传输数据时延的约束条件下，讨论无人机能效问题，为此，文中针对单架无人机覆盖多个用户的场景，通过优化无人机的高度，最大化无人机能效，提出用户服务质量约束下无人机能效优化算法(energy-efficient optimization algorithm under quality of service constraints, EEOA)。采用NOMA技术，用户向无人机传输信号，接收端(无人机)采用SIC技术分离各用户信号。

主要研究内容包括：

1) 构建最大化无人机能效的目标函数，并考虑两个约束条件：无人机高度和用户通信服务质量。服务质量包含两项指标。第一项指标是用户端信噪比不小于预设阈值，该指标保证无人机端能够成功解码用户信号；第二项指标是无人机为用户提供充足的服务时间，该指标保证每个用户有充足的时间向无人机传输数据。

2) 通过对目标函数进行处理，将两个约束条件转换成关于无人机高度的函数。

3) 求解目标函数，获取无人机能效最大化的无人机高度值。

1 系统模型

1.1 网络模型

考虑如图1所示的网络模型，将网络中一个无人机作为空中基站和无线接入点。UAV收集在其覆盖范围内用户的数据。这些用户均匀分布在UAV在地面的覆盖区域内。此外，无人机在地面上配备控制器，该控制器控制UAV的位置。

图1 网络模型

假定无人机配备半功率波束的有向天线，依据文献[12-13]可知，天线在方向(φ,ω)上的增益为：

(1)

式中g0≈2.2846[12]。

所有用户配备全向天线，在相同时间和频率资源上向无人机发送自己的数据。但是所有用户发送数据的功率不同，因此它们形成上行链路的功率域-NOMA(power-NOMA, P-NOMA)网络模型。通过P-NOMA方案，信号相互正交，避免干扰。无人机端利用SIC技术解码各用户信号。

1.2 信道模型

无人机与用户间链路可能为视距链路，也可能为非视距链路，这取决于无人机与用户间的相对位置。依据文献[14-15]，用户与无人机间链路呈视距链路的概率为：

(2)

式中：φi表示用户向无人机传输信号的仰角,φi=(180/π)arctan(hu/ri)，ri表示用户离无人机在地面覆盖区域中心点位置间距离，hu表示无人机盘旋的高度；a,b为环境参数。

路径衰耗的概率均值为[15]：

(3)

式中：μ1和μ2分别表示视距链路和非视距链路的路径衰耗均值；h0表示在1 m的参考距离下的信道增益。

2 问题描述

2.1 上行的P-NOMA的传输模型

蜂窝系统中上行链路功率控制机制要求来自不同用户的接收功率均等于目标功率pu。因此，用户i的传输的功率为：

(4)

为了能够成功地解码接收的消息，无人机要求不同用户采用不同功率传输消息。为此，用户先通过正交控制信道，并以相同功率向无人机传输各自的控制消息。收到所有用户的消息后，无人机就依据相应的路径衰耗值给所有用户设置解码顺序编号。编号原则为:路径衰耗值大的用户，就设置大的解码编号；反之，路径衰耗值小的用户，就设置小的解码编号。

如图2所示，无人机通过SIC技术检测用户信号[15]。假定无人机覆盖了J个用户，用户U1离无人机最近，用户UJ离无人机最远。无人机先解码信道质量最佳信号，即信道增益最大的信号最先被解码出来。因此，用户U1最先被解码，其解码编号为1。

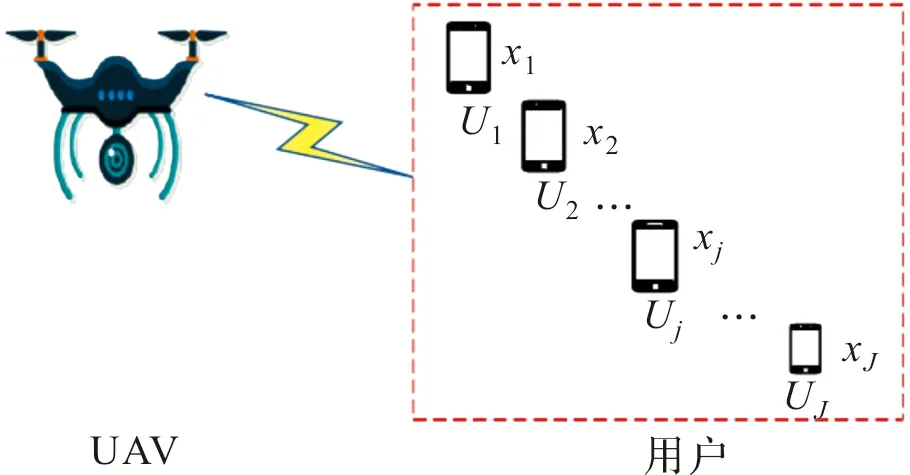
图2 NOMA上行链路

当收到解码编号后，用户i就利用解码编号对传输功率进行控制：

(5)

式中：δ表示功率衰减因子；n(i)表示用户i的解码编号。

各用户依据各自的功率向无人机传输消息后，无人机所接收的信号为：

(6)

接收了信号后，无人机就依据解码编号解码各用户的信号。在解码某特定用户信号时，其他还未解码的信号对该用户信号形成干扰，换而言之，仅当前(n(i)-1)用户的消息被解码后，才能解码用户i的信号。因此，从用户i接收的信干比(signal interference noise ratio, SINR)为：

(7)

(8)

依据香农公式，用户i所获取的速率为：

(9)

2.2 能效

将无人机覆盖区域面积与无人机所消耗的总能量之比定义为能效：

(10)

Pt(hu)=Pu(hu)+Pc

(11)

式中：Pu(hu)表示无人机盘旋在高度为hu时所消耗的能量,Pu(hu)=αuhu+βu；Pc表示无人机作为无线接入点时所消耗的能量。

2.3 构建目标问题

在满足无人机高度和用户服务质量的约束条件下，最大化无人机能效，可构建如式(12)所示的目标优化问题：

(12)

约束项为：

hmin≤hu≤hmax

(13)

(14)

(15)

式(13)对无人机的飞行高度进行限制，式中：hmin,hmax分别表示无人机飞行高度的最小值、最大值；式(14)确保无人机能够解码从用户端所接收的所有消息；式(15)确保了每个用户均有充足时间向无人机传输数据。

3 P1问题的转换及求解

先将P1问题进行变换，使其都是关于无人机高度的函数，再利用二分法求解。

3.1 P1问题的转换

(16)

证明过程为：

将式(5)代入式(7)，可得：

(17)

(18)

当hu=hmin时，Nmin(h′min)=ρuπ(h′min)2tan2θ，将其代入式(16)可得：

(19)

因此，利用命题1，式(14)和式(15)可分别写成：

(20)

(21)

将式(5)代入式(20)可得：

(22)

再将服务质量约束转换成高度约束条件：

(23)

通过上述等式转换，最终P1问题被转化成：

(24)

约束项：

(25)

从式(24)可知，P2问题的分子和分母都是关于hu的增函数。

3.2 基于二分法的P2问题的求解

先计算EEn(hu)关于hu的一阶微分特性：当hu取hopt时，EEd,n(hopt)=0；当∀hu∈(hmin,hopt),则EEd,n(hu)>0；当∀hu∈(hopt,hmax)，则EEd,n(hu)<0，其中EEd,n表示EEn的一阶微分函数：

(26)

4 性能分析

通过数值评估EEOA算法的性能。仿真参数取值如表1所示。

表1 仿真参数取值[16-17]

4.1 基准算法

为了更好地分析EEOA算法性能，选择均衡正交多接入(orthogonal multiple access, OMA)算法[16]作为参照。在OMA算法中，用户i所获取的速率：

(27)

引用命题1，可得到OMA算法的能效：

(28)

4.2 能效随飞行高度的变化情况

首先，分析EEOA算法和OMA算法产生的能效，分别依据式(24)和式(28)计算能效，如图3所示，其中δ=1.5，γn=10。图中的AEEo(hu)，AEEn(hu)分别表示OMA算法、EEOA算法的能效。

图3 能效随飞行高度的变化情况

正如所预料的，获取最大的能效既不是在最低的飞行高度，也不是在最高的飞行高度。在低的飞行高度期间，能效随hu的增加而上升，原因在于：依式(24)可知，无人机覆盖的面积越小，就过度补偿了无人机本身能耗的减少。而在高的飞行高度区间，能效随hu的增加而下降，原因在于：在高的飞行高度区间，无人机需要消耗更多时间去完成数据传输，这就增加了无人机的能量消耗。能量消耗量随飞行高度的增加而增加。

此外，相比于OMA算法，提出的EEOA算法能够获得较高的能效。同时，观察图3不难发现，OMA算法和EEOA算法的能效随飞行高度呈钟形，其最优高度值均可通过算法1获取。

4.3 最大能效随用户密度的变化情况

分析不同用户密度对能效的影响，如图4所示，其中γn=6。

图4 最大能效随用户密度的变化情况

从图可知，用户密度的增加，使OMA算法和EEOA算法的最大能效下降。原因在于：用户密度越大，覆盖区域内的用户数越多，这必然增加了无人机的能量消耗，最终就降低了能效的最大值。

此外，相比于OMA算法，EEOA算法的能效性能得到提高。但是随着δ值的增加，EEOA算法的能效优势逐步下降。

通过上述分析可知，提出的EEOA算法能够提高能效。同时，当用户密度较小时，小的δ值可以获取更高的能效。

5 总结

针对应急保障通信的无人机作为空中基站的应用场景，提出用户服务质量约束下无人机能效EEOA优化算法，基于用户服务质量约束条件，通过优化无人机高度，提升无人机能效。通过构建满足用户服务质量约束条件下的目标函数；再经数学处理转换，形成关于无人机高度的函数；最后，利用二分法求解，得到最优的高度值。仿真结果表明，提出的EEOA算法提升了无人机能效。此外，无人机能效与用户密度、功率衰减因子成反比。下一步，将重点研究下行链路的能效问题以及多个无人机的协同工作。