湿微下击暴流对火炮外弹道精度影响分析

王 晋，田军委,，刘雪松，张 杰，张 震

(1 西安工业大学兵器科学与技术学院，西安 710021；2 西安工业大学机电工程学院，西安 710021；3 内蒙古北方重工业集团有限公司，内蒙古包头 014030)

0 引言

影响火炮外弹道射击精度的因素多种多样，据研究表明，在影响火炮射击精度的诸多因素中，气象条件产生的影响占比70%以上[1]，其中低空风切变对火炮外弹道的影响较为典型。作为众多低空风切变类型中的一种，微下击暴流因其尺度小、强度大、生命周期短、无法及时预报等特点，成为了对飞行安全影响严重的危险气流[2-3]。近年来，国内外相关学者主要围绕干微下击暴流展开了大量的研究，其中Sengupta等[4]采用大涡模拟(large eddy simulation, LES)方法对微下击暴流进行模拟并开展数值分析；Kwon等[5]建立了关于长脉冲持续时间情况下非平稳波动的闭合模型，以快速评估非平稳湍流效应；张涛等[6]通过测得实际数据对微下击暴流进行了结构分析与形成机理研究；刘时杰等[7]利用插值法对涡环速度场进行处理并进行线性叠加，验证结构的有效性；陶杨等[8]基于涡环原理建立有限粘性涡核模型，解决了涡核内部速度分布不连续问题；陈健伟等[9-10]将干微下击暴流模型与火箭弹外弹道模型相结合，并分析其对火箭弹外弹道的影响，取得了一定的成果。但与干微下击暴流不同，湿微下击暴流中会出现短时强降水现象[11-12]，增大弹丸飞行过程中的空气阻力，对火炮射击精度的影响较为明显，同时由于火炮弹丸与火箭弹的气动外形，发射方式不同，受到湿微下击暴流的影响也存在差异。

文中基于涡环原理与流体力学建立微下击暴流与雨滴运动模型融合为湿微下击暴流模型，分析湿微下击暴流的气流特性，并将该模型与火炮质心弹道方程相结合，仿真并分析不同初始涡环中心诱导速度对火炮在平射与曲射两种发射方式下射击精度的影响。

1 气流风场建模

微下击暴流是以降水的拖曳作用作为动力，在降水过程中，由于雨水的蒸发作用使得周围空气温度降低，导致上升气流崩塌，下沉气流将其替代，撞击地面向四周扩散并上扬[13]，从而形成下击暴流。如图1为微下击暴流形成的过程，在该特性气流影响区域中，不同位置气流对火炮外弹道的影响也各不相同。

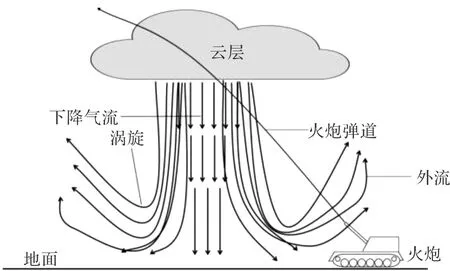
图1 微下击暴流形成示意图

1.1 干微下击暴流模型构建

基于涡环原理[14]对微下击暴流模型进行构建，将地面坐标系作为参考系，设主涡环中心为Oa，其坐标点为(xa,ya,za)，镜像涡环中心为Ob(xb,yb,zb)，弹丸位置为Oc(xc,yc,zc)，涡环半径为R，当主涡环与镜像涡环平行于地面时，主涡环曲线方程[9]为：

(1)

在实际情况中，主涡环与镜像涡环分别与地面存在夹角φ，其示意图如图2所示，通过将三维倾斜涡环投影到XOZ面上形成二维图形，此时弹丸在飞行过程中任一位置与主涡环距离极值为：

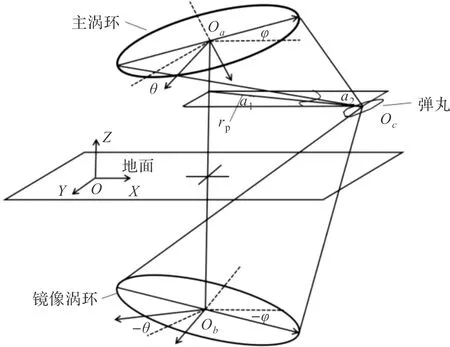
图2 倾斜涡环示意图

(2)

同理弹丸与镜像涡环距离极值为：

(3)

在Oc点主涡环的流函数φa[9]为：

(4)

ka=|(rmax1-rmin1)/(rmax1+rmin1)|

(5)

Γ=2Rv0

(6)

其中：Γ为涡环强度；F1(ka)，F2(ka)为椭圆积分函数；ka为椭圆积分变量；v0为初始气流速度。

经过简化计算[10]，当0≤ka≤1时，

(7)

同理可求出镜像涡环的流函数φb,其表达式[10]为：

(8)

kb=|(rmax2-rmin2)/(rmax2+rmin2)|

(9)

主涡环与镜像涡环的径向、轴向诱导速度可分别对两个涡环流线方程求偏导得出，其表达式为：

(10)

将两个涡环的径向速度在地面坐标系下进行分解，可求出沿Ox轴与Oy轴方向速度，其表达式为：

(11)

将主涡环与镜像涡环方程进行叠加，将各轴诱导速度进行线性叠加，可得到Oc点的流线方程和速度方程，其表达式为[7]：

φc=-φa+φb

(12)

(13)

由速度方程可知，当Oc点与涡核之间的距离增大时，诱导速度会逐渐减小，但当Oc点与涡核之间的距离为0时，诱导速度会呈+∞，不符合实际情况。如图3所示为微下击暴流涡环原理。因此引入诱导因子ξ，建立连续变化的涡核模型，其表达式为[8]：

图3 微下击暴流涡环原理图

(14)

式中：R为主涡环半径；r为涡核截面半径。

阻尼系数随最小距离rmax1的变化如图4所示。

图4 阻尼系数随最小距离rmin1的变化图

因此诱导速度修正后可表示为：

(15)

由式(10)可知，式中rp不能为0，不符合实际情况，因此为了解决这个问题，基于湍流自由射流理论分别建立主涡环与镜像涡环中心轴的轴向诱导速度，如图5所示。涡环外任一点c的速度位函数φ为[15]：

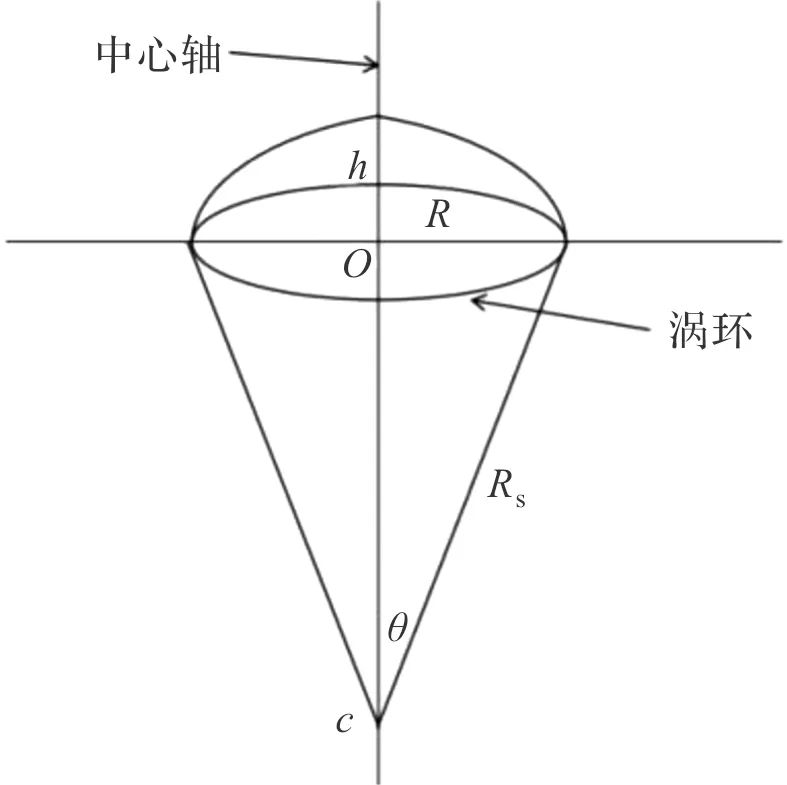
图5 涡环中心诱导速度

(16)

(17)

式中：Ω为c点的立体角，即辐射球面上的部分面积ΔS与整个球面积之比。因此可得：

Ω=2π(1-cosθ)

(18)

(19)

对φ求偏微分可得：

(20)

根据主涡环、镜像涡环与c点的相对位置关系可得出z1=za-zc，z2=za+zc，然后将其分别代入式(20)，可得主涡环与镜像涡环中心轴的轴向诱导速度：

(21)

(22)

因此中心轴OaOb处轴向合速度为：

vz2=vza-vzb

(23)

由于涡环与地面存在夹角，其中主涡环与地面夹角向量为(φθ0)T，因此引入俯仰变换矩阵Lθ与滚转变换矩阵Lφ完成主涡环和镜像涡环的坐标系转换[10]。

(24)

(25)

(26)

1.2 雨水与气流融合的湿微下击暴流模型构建

对于湿微下击暴流，雨水在降落过程中并不会马上被完全蒸发，势必会对火炮外弹道产生一定的影响。基于流体动力学理论，建立雨滴运动轨迹方程[16]：

(27)

(28)

(29)

(30)

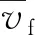
(31)

对式(31)求积分可得：

(32)

由于雨滴下落时间与火炮弹丸飞行时间不能统一，为避免计算冲突，通过求解微分方程将雨滴下落时间用其他量替代，即得出下落时间与下落位置的关系，其计算步骤为：

(33)

(34)

(35)

其中：h2为雨滴不同时刻下落高度；h1为雨滴下落总高度；H为不同时刻雨滴距离地面高度。将式(35)代入式(32)中并化简可得：

(36)

因受到气流的影响，雨滴与地面存在夹角，将雨滴落速进行坐标系转换，其转换后速度方程为：

(37)

式中α为速度vx与地面坐标系x轴正向夹角。

由于飞行中的弹丸为高速自旋刚体，其周围存在的空气附面层被带动，使得雨滴很难通过直接接触弹丸表面的方式对其施加作用力影响弹丸飞行轨迹，因此为了准确分析雨水与气流对外弹道产生的综合影响，特将气流与雨水进行等效替代，其替代方程为：

(38)

由于替代后空气状态特性发生改变，不能通过弹道方程准确计算出弹道偏差，为让替代方程得以适用，需将近地空气密度、压强等状态参数进行修正，修正方程为：

(39)

(40)

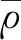
2 火炮6自由度外弹道方程

为分析微下击暴流对火炮外弹道产生偏差的影响，根据火炮体外弹道学理论，建立弹丸6自由度弹道方程，采用Runge-Kutta法进行解算[17]。

2.1 计算偏差的6自由度弹道方程模型

为了分析微下暴击气流对火炮外弹道产生偏差的影响，利用仿真软件建立火炮外弹道6自由度运动方程，其表达式[18]为：

(41)

式中：ΩE为地球自转角速度；αN为射向角；r0为地球半径。

2.2 四阶Runge-Kutta法

Runge-Kutta法是基于泰勒级数改进的一种算法，该方法计算精度高，是计算火炮外弹道的一种主要算法，其表达式[19]为：

(42)

时间步长取0.005 s，基于Runge-Kutta法计算火炮外弹道，迭代4次即可满足精度要求。

3 仿真及结果分析

将火炮质心运动弹道模型与微下击暴流风场模型相结合，以某型155 mm杀爆弹为研究对象，其技术参数如表1所示，研究该类风场对火炮外弹道射击精度影响。

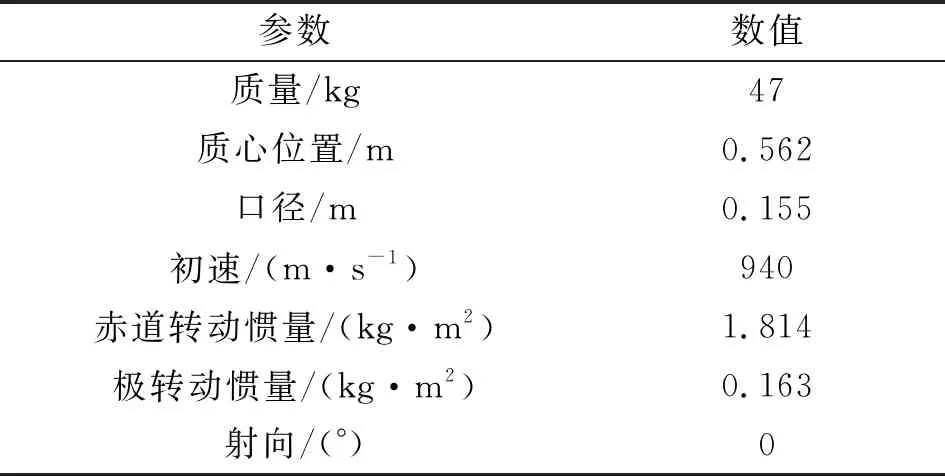
表1 某型155 mm杀爆弹技术数据

3.1 气流模型仿真

根据上述数学模型，设置涡环参数：主涡环中心坐标Oa(3 000 m, 3 000 m, 800 m)，半径R为1 000 m，涡核r为100 m，初始涡环中心诱导速度v0为10 m/s，涡环倾斜角度为30°。图6、图7分别为干微下击暴流不同高度上水平气流速度和垂直气流速度，取向右、向下方向为速度正方向，由于主涡环与地面呈30°夹角，且左侧低右侧高，因此气流在中心点偏右方向速度较偏左方向速度略大，且在垂直方向上，中心点右侧下沉气流撞击地面时速度与左侧气流速度相比约大10 m/s。

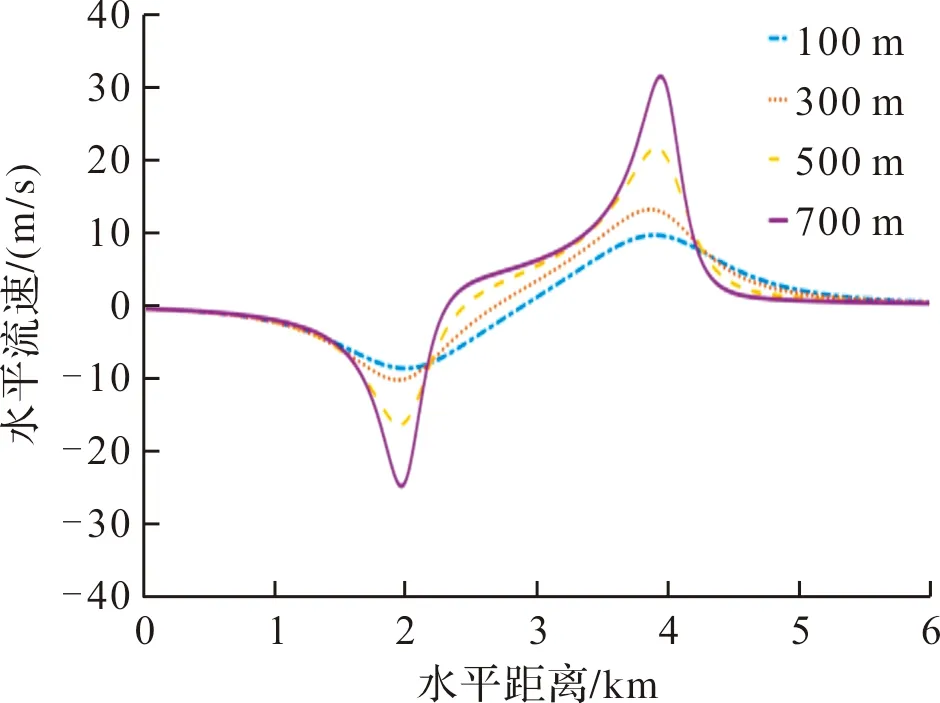
图6 干微下击暴流不同高度水平流速

图7 干微下击暴流不同高度垂直流速

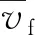
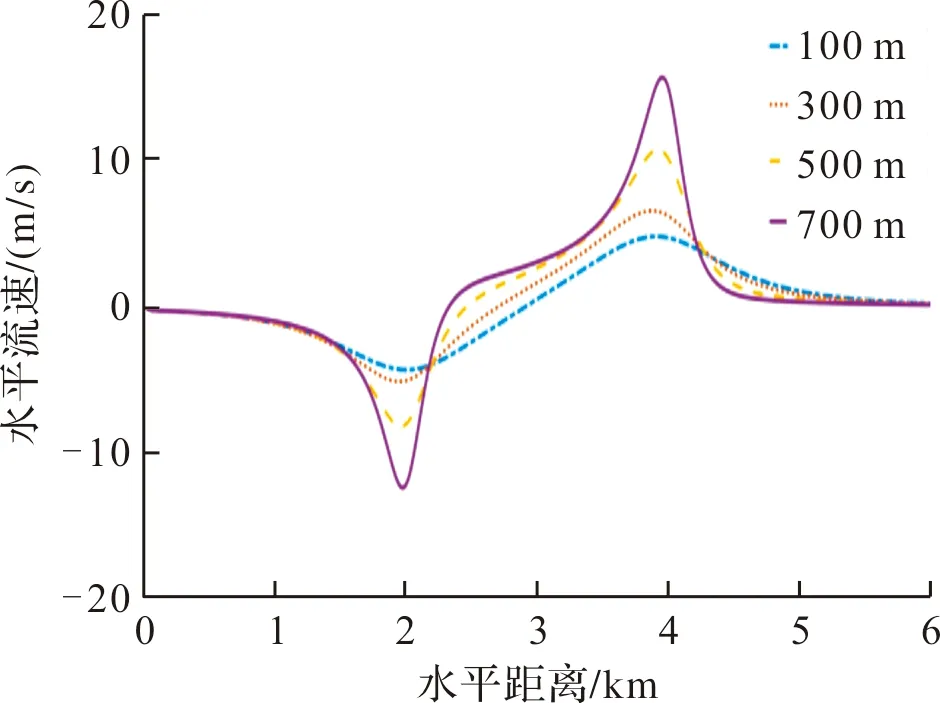
图8 不同高度湿微下击暴流水平流速

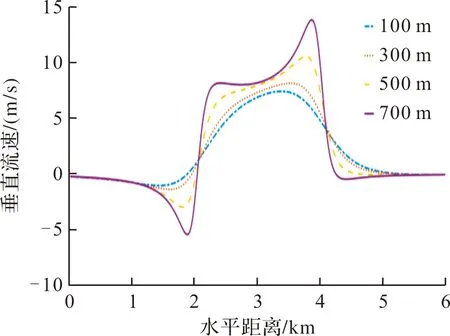
图9 不同高度湿微下击暴流垂直流速

由图10、图11可知，对于高度较低的水平融合型气流，如高度为100 m时，其速度大小及分布近似关于涡环中心位置对称，与理想环境下水平涡环气流速度大小与分布类似，涡环倾斜对此类低高度水平气流流速影响较小。

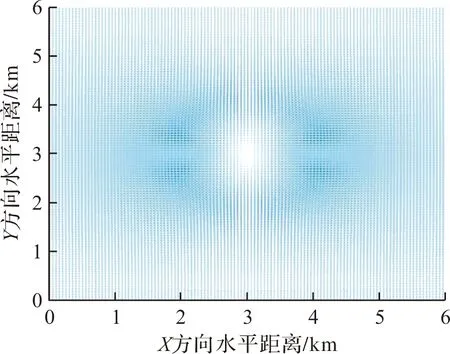
图10 高度为100 m时湿微下击暴流水平流速

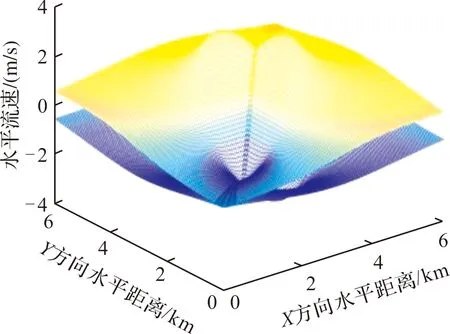
图11 高度为100 m时湿微下击暴流水平流速三维图

3.2 不同中心诱导速度对火炮低伸弹道影响

当目标距离较近时，常采用小射角的方式利用火炮对目标进行打击。但火炮小射角射击时，其外弹道射高较低，射距较近，易受到近地低空气流影响，由于微下击暴流涡环高度与直径远大于火炮低伸弹道的射高与射距，因此弹丸在飞行过程中会全程受到微下击暴流的影响。

根据JAWS雷达测量结果以及FDR数据记录器记录微下击暴流数据[10]，设置中心涡环气流诱导速度为10 m/s，15 m/s，20 m/s，25 m/s，其余涡环及气流等数据参照3.1节，并与无风环境做对比，火炮射角为1°，图12为不同诱导速度与弹道射程、侧偏的曲线。

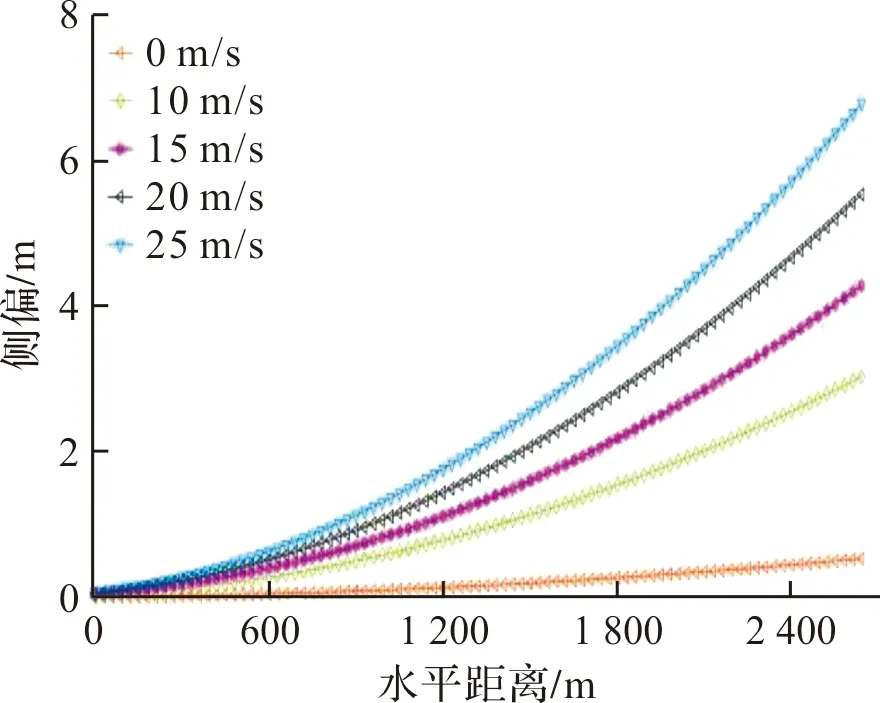
图12 不同诱导气流与外弹道射程、侧偏曲线

实验数据如表2所示，由于受到下沉气流与降雨的影响，弹丸垂直下降速度增快，飞行时间缩短，因此随着诱导速度的增加，弹丸的最大飞行高度、落点速度、射程随之降低，与无风状态下数据相比，降低比率均小于1%，影响较小；但侧偏与落点偏航角随着诱导速度的增大而增大，相对于无风状态数据，诱导速度在10 m/s时，其侧偏与偏航角分别增大770%、747%，且诱导速度每增加5 m/s，侧偏与偏航角相对于前一项以同样的比率分别增加约45%、36%、24%。

表2 不同诱导速度对火炮低伸弹道影响

3.3 不同中心诱导速度对火炮远距离射击精度影响

对于远距离攻击目标，常采用大射角、高初速的曲射方式发射弹丸，由于射角大、初速快、火炮的最大射击高度较高，弹丸会在极短时间内穿越涡环，因此在弹丸部分上升阶段会受到湿微下击暴流影响。将火炮射角设置为45°，射击位置设置在涡环中心轴线右侧，穿越点在涡环中心附近，且涡环外环境为无风环境，其余参数参照3.1节，图13为不同诱导速度下火炮外弹道轨迹图。

图13 不同诱导速度下火炮外弹道轨迹图

实验数据如表3所示，由于涡环高度低、弹丸初速高，因此穿越涡环时间短，受到微下击暴流的影响比较有限。通过实验数据可知，与无风环境数据相比，中心涡环气流诱导速度的增加对火炮的射程影响较为明显，相比于无风环境下，在10 m/s的诱导速度下，射程减小约2.7%，且诱导速度每增大5 m/s，相比于前一项射程减小约1.3%。

表3 不同诱导速度对火炮远距离射击精度影响

4 总结

基于涡环原理与流体力学建立微下击暴流与雨滴运动模型，并融合为适用于弹道分析计算的湿微下击暴流模型，通过引入6自由度弹道方程分析融合模型对某型155 mm火炮射击精度的影响。根据仿真结果，对于低伸弹道，不同中心诱导速度对外弹道侧偏与偏航角影响明显，但随着诱导速度的增加，侧偏与偏航角的增加比例也随之减小；而对于远距离射击时，不同中心诱导速度对火炮的射程影响较为明显，在10 m/s的诱导速度下射程比无风环境射程减小约2.7%，且诱导速度每增大5 m/s，射程减小约1.3%，严重影响火炮射击精度及杀伤效果。

上述研究为火炮在湿微下击暴流环境中射击提供理论参考，对于火炮外弹道应用研究具有积极的意义。但实际发射过程中，气象条件较为复杂且有多种特性气流共存的可能性，如何将研究与其他特性气流进行融合并分析其对火炮外弹道的影响，以及如何对火炮在该类环境下落点产生的偏差进行修正，还有待进一步研究。