不变量与五声性十二音序列的变换网络

许 琛

在某种变换下，一个系统的某种物理量保持不变，则称此物理量为“不变量”（invariant）。美国当代作曲家米尔顿·巴比特在《作为作曲决定因素的十二音不变性》①Milton Babbitt: “Twelve-Tone Invariants as Compositional Determinants” , The Mиsical Qиarterly, Vol. 46, No. 2, Apr., 1960, pp. 246-259.一文中，首次将数学中的“不变量”概念引入音乐分析，使十二音序列作曲方法上升为系统谨严的理论，其序列思维对西方当代音乐理论与创作产生了深远影响。②陈小兵：《十二音的不变量——巴比特序列思维研究札记》，《黄钟》1997 年第3 期，第34 页。以此为发端，阿伦·福特在《无调性音乐的结构》中，就集合在移位、倒影等变换下所产生的不变音级的具体生成条件进行了系统阐释，并强调：“不变性的概念和发展、变化、连贯与间断等直觉音乐概念有着密切的关系。由于在无调性音乐中不变性有着如此根本的重要性，以致了解它的基本原理是十分重要的。”③［美］艾伦·福特：《无调性音乐的结构》，罗忠镕译，上海：上海音乐出版社2009 年版，第37 页。约瑟夫·斯特劳斯在《后调性理论导读》④Joseph N. Straus: Introdиction to Post -Tonal Theory, New York: W.W. Norton & Company， 2016.中，兼容并包巴比特用以决策序列音乐作曲的“不变量理论”以及列文“十二音音乐截断联系”理论⑤David Lewin: “A Theory of Segmental Association in Twelve-Tone Music” , Persрectives of New Mиsic, Vol.1, No.1, Autumn, 1962, pp. 89-116.，发展了福特的“音级集合理论”，讨论了序列在某种变换下保持的不变性二音对子、不变性三音和弦等现象。郑中在《〈鸟儿的小小素描〉之不变量与变量分析》等文中⑥郑中：《〈鸟儿的小小素描〉之不变量与变量分析》，《黄钟》2006 年第2 期，第10—18、60 页；郑中：《梅西安〈鸟类志〉之分析》，《中央音乐学院学报》2005 年第4 期，第73—75 页。，将不变量理论扩大至更为广阔的后调性音乐世界，就梅西安“与鸟类对话作品”中蕴藏的不变性素材进行提取量化。

关于不变量与不变性等问题的研究，不仅适用于西方无调性思维的十二音技法音乐的创作与分析，更可以为探索作为无调性的十二音技法与有调性的五声音阶的综合体——五声性十二音序列音乐的音高逻辑与形式分析提供新的路径和策略。

一、极小值不变性与互补的 五声性十二音序列

音程向量中若有分量的值为0，那么取该分量所对应的音程数作为移位值进行移位变换，变换双方将没有共同音交集，不变性音级的数量为0，在变换过程中实现极小值不变性。相对的，取音程向量中最大值分量所对应的音程为移位值进行移位变换，则变换双方所持的不变音级的数量可最大化。

互补的五声性十二音序列中，最明显的是序列内部各宫系统对共同音的保留。这种不变量的生成取决于一个必要条件，即根据与宫系统等价的五声性音级集合的音程向量，所采取的特定的移位值。

（一）移位值与十二音序列五声性截断移位变换中的极小值不变性

在互补的五声性十二音序列中，互为补集的五声性截断可被视为一种移位关系。五声音阶的集合标记为5—35，其音程向量［032140］决定了取d1=0 或d6=0 所对应的音程数，即以1（小二度音程）、11（大七度音程）或以6（增四/减五度音程）为T 值进行移位变换，变换双方将不存在交集，即在移位变换过程中不会产生共同音，实现极小值不变性，对写作“互补的五声性十二音序列”有重要意义。

1. T1/11与移位变换中的极小值不变性

以罗忠镕的《牵牛花》⑦华铃诗、罗忠镕曲：《牵牛花（女高音独唱）》，《中国音乐》1982 年第2 期，第65 页。和黄育义的《溪声》⑧徐訏诗、黄育义曲：《溪声》，《音乐创作》1988 年第3 期，第13 页。为例（见谱1a、1b），两首艺术歌曲的序列主题都可被视为建立在♭G 宫系与G 宫系之上的“互补的五声性十二音序列”。宫音以1 或11 为T 值进行移位的两个宫系统相距半音，关系最远，没有共同音，相互独立，实现了极小值不变性。

谱1a 《牵牛花》（罗忠镕曲）互补的五声性十二音序列原型P2（人声部分）截断1

谱1b 《溪声》（黄育义曲）互补的五声性十二音序列原型P4截断1

诚然，两个没有交集的五声宫系无法覆盖十二音序列全部音级（余两个音）。那么，让我们换一种截断方式，基于五声与均七声来观察《牵牛花》和《溪声》主题序列内部的变换逻辑。如谱2a、2b 所示，两首艺术歌曲的主题序列可被分割为由G 宫五声音阶和♭G 均七声音阶，或由F均七声音阶和♭G 宫五声音阶前后接续而成。作为互补的五声性十二音序列，无论是5+7，还是7+5 组合，宫音（五声音阶）与均主（七声音阶）之间均为半音关系，两个音阶之间没有共同音，相互独立，互补为一个完整的五声性十二音序列。

谱2a 《牵牛花》互补的五声性十二音序列原型P2（人声部分主题）截断2

谱2b 《溪声》互补的五声性十二音序列原型P4截断2

2. T6与移位变换中的极小值不变性

笔者尝试将《溪声》序列中的第6 个音与第10 个音互换位置，可得一对相距三全音关系的五声音阶。宫音以6 为移位值的两个五声音阶在移位变换中无共同音级关联，实现极小值不变性，加之一对增四/减五度音程音，互补为五声性十二音序列。

谱3 《溪声》互补的五声性十二音序列原型P4的变形

基于对五声性截断移位变换过程中实现极小值不变性生成机制的考察，我们可以总结出一些基于五声性框架的互补的五声性十二音序列组合的设计基本原则（但这并不全面，有待下文进一步补充）：

组合一：六声（五声带清角）+六声（五声带变宫），在两个相距半音的五声宫系之间，加入一个纯四度关系二音对子，以合成为一列互补的五声性十二音序列。纯四度音程中的根音可被视为宫音音级数较大的宫系之清角音，而音程中的冠音可被视为宫音音级数较小的宫系之变宫音。在实际写作中，偏音是两个相距半音的五声宫系统之间的桥梁，它们往往或前或后紧挨着其所隶属的宫系五声音阶以形成完整的五声性六音截断。不过，由于这些六声音阶或以偏音始，或以偏音终，并不构成对于宫音的强烈倾向。

以《牵牛花》为例，二音对子中的音级C为G 宫系统中的清角音，音级F 则为♭G 宫系统中的变宫音。为加深序列中人们关于五声性的主题形象和听觉印象，人声部分的序列主题在初次呈现时便被拆分成两个带偏音的六声音阶截断，与二分性歌词断句“我是一朵牵牛花，哑的铃”紧密联系（见谱4a）。此外，六声音阶还具有音乐主题的作用，贯穿器乐前奏部分始终，始于♭A 宫六声，落于G 宫六声（见谱4b）。

谱4a 《牵牛花》十二音序列主题P2之带偏音的六声音阶截断（声乐部分，第4—6 小节）

谱4b 《牵牛花》十二音序列主题P3之带偏音的六声音阶截断（钢琴前奏部分，第1—3 小节）

组合二：六声（五声带清角）+六声（五声带清角）/六声（五声带变宫）+六声（五声带变宫），在两个相距增四/减五度音程的五声宫系之间，加入一组增四度旋律音程，以合成为一列互补的五声性十二音序列。增四度音程中的根音若被视为宫音音级数较大的宫系之清角音，则音程中的冠音被视为宫音音级数较小的宫系之清角音；若增四度音程中的根音被视为宫音音级数较大的宫系之变宫音，则音程中的冠音被视为宫音音级数较小的宫系之变宫。

组合三：五声+七声，互补的五声性十二音序列由一个五声音阶加一均（七声）组合而成，五声宫音与七声均主音之间相距半音音程。

（二）五声旋法与序列原型—倒影变换中的极小值不变性宫系

除了共同音，五声性十二音序列变换中的不变性还反映在序列原型—倒影变换中的不变性宫系。宫系被保留的数量，取决于一个必要条件，即倒影轴音的选择。对于一个互补的五声性十二音序列来说，序列的起始音级，一般来说隶属于某一宫系统下，是以宫角轴、商为轴还是以徵或羽为轴，决定着原型—倒影变换中的是否生成不变性宫系。

序列原型—倒影变换中的极小值不变性宫系是指在变换过程中，随着宫系统的推移，原型与倒影序列之间不存在共同宫系。以五声性十二音序列原型上首个宫系的徵音或羽音为轴进行倒影变换，均可在变换过程中实现极小值不变性宫系。

1.羽轴与倒影变换中的极小值不变性宫系

“花间一壶酒，独酌无相亲。”借方位隐喻，房晓敏在其十二音序列艺术歌曲《月下独酌》⑨［唐］李白诗、房晓敏曲：《月下独酌》，《音乐创作》1989 年第1 期，第38 页。中使用由两个相距半音的六声宫系互补而成的序列形式与诗人清冷孤独的内在精神相贯通。在起承转合的诗歌体中，音乐相继完成了序列原型P8—原型的逆行R9—原型的倒影I8—原型的逆行倒影RI7等一系列序列变换。以点带面的艺术路径承担着音乐创造性、简约性发展的内在动力，这是一曲基于五声性音高材料之上的层次分明的有机体。作曲家紧扣诗词中的“对影”一词展开想象，以序列倒影的形式呼应诗人的浪漫主义气息。伴随着力度与音区的逐渐攀升，以原型序列中的♯G 为轴（B 宫系羽音）进行倒影变换，变换后得♭A、G两宫系，实现了极小值不变性宫系。以倒影为法，以羽生宫，主宫生多象，对影成四宫。“举杯邀明月”——西方十二音序列技法形式的原则，与五声旋法、“鱼咬尾”相对⑩详见谱6 框示部分。其中，B 宫羽音♯G 以等音等同的关系变换为♭A 宫系之主音，以鱼咬尾的方式接续了诗的上片与下片。——“对影成三人”。全曲组织严密一气呵成，乐节之间、乐句之间环环相扣连绵不绝，音乐与诗歌融为统一的艺术整体。

谱5 《月下独酌》（房晓敏曲）五声性十二音序列原型P8与倒影I8（羽=♯G/♭A，羽轴）

谱6 《月下独酌》呈示段序列原型及其变换（声乐部分，第4—20 小节）

2.徵轴与倒影变换中的极小值不变性宫系

作为组合型十二音序列，由马友道所作的艺术歌曲《西江月》⑪［宋］辛弃疾诗、马友道曲：《西江月》，《上海歌声》1988 年第4 期，第29 页。，其序列主题既可被视为由六个二音音列组成，也可作重叠排列的三个五声音阶的排列，尤其以两端的D 宫五声和♭E宫五声被强调地呈示出来。如谱7 所示，原型序列P9起始于音级A，D 宫的徵音，以其为轴形成的倒影序列I9⑫《西江月》为无再现三段式，倒影序列I9 被用于第三段，作倒影序列的逆行RI1。，其两端则被推移为C 宫五声和B 宫五声，而不再复现原型序列中的任一宫系。

谱7 《西江月》（马友道曲）五声性十二音序列原型P9与倒影逆行I9（徵=A，徵轴）

该主题序列P9亦由六组对音组成。在两个五声宫系的移位变换中，始终保持每组对音大二度音程关系不变，每两个对音组之间保持了纯四/纯五度音程不变。如此一来，《西江月》的12 个音级序进可分为三个阶段，每个阶段实现同样数量的对音组数，进而生成五声性十二音序列的三个不变性四音子集（4—23）。该序列中最明显的不变量是各个移位四音子集中“2,5,2”音程数数列的保留。

谱8 《西江月》五声性十二音序列原型P9中的不变量：6 组对音、3 个不变性四音子集及音程数数列“2,5,2”

二、极大值不变性与五声性 十二音序列的变换网络

序列原型—倒影变换中的极大值不变性，是指在变换过程中，倒影序列产生同样数量的宫系统，且宫音保持不变。

（一）商轴与倒影变换中的极大值不变性宫系

《西江月》主题序列P9中的三个不变四音子集4—23，其音响实质为具有五声性的四声音阶（见谱9）。G（D）宫四声，B（♯F）宫四声和♭E（♭B）宫四声用于诗词上阕，分别对应“明月清风”“惊鹊鸣蝉”等声景。四声曲调古朴悠扬，引人入胜。前文“路转”，后文“忽见”。马友道以原型P9首宫G（四声）之商音A 为轴行倒影变换，得序列I9，其开篇仍属G 宫四声，后续♭E 和B 两宫。至此，在P9和I9上已实现了对3 个四声宫系的全部保留。将I9再以逆行为序，置G 宫四声于尾，终于商音，复见“明月”。实现极大值不变性宫系的整个倒影变换过程，既衬出了词人骤然间看出了分明临近旧屋的欢欣，又表达了曲作者沉浸在“十二个音天外，两三调五声前”中怡然自得的入迷程度，相得益彰。曲作者有着词人潜心的构思，深厚的艺术功底，令人玩味无穷。

五度相生，对称平衡，是传统五声调式音阶“宫商角徵羽”的内在规律和审美诉求。在一个宫系统内，在一个音高空间中，存在着唯一一对互为倒影对称着的音列，即以商音为轴互为倒影的宫调式与角调式。以商音为轴，其它四个音级作倒影变换后，仍得其自身。比之马友道的《西江月》，罗忠镕在《涉江采芙蓉》《牵牛花》等艺术歌曲的创作中，已然更早地认识到“商核论”的理论价值与实践意义。“以商为轴”被广泛地用于决策五声性十二音序列中去。

谱9 《西江月》五声性十二音序列原型P9与倒影逆行RI9（商=A，商轴）⑬出于对旋律歌唱性的考虑，序列RI1 中的第5 个音♭E 和第6 个音F 互换了位置。

谱10 《牵牛花》五声性十二音序列原型P2与倒影I2（商=D，商轴）

《牵牛花》的五声性十二音序列原型P2起始音为D，因以C 宫系统（F 均）的商音为轴进行倒影变换，变换后仍得其自身（倒影序列I2上的1—7 音），余下的8—12 音为♯F 宫五声，与原型中的♭G 宫五声为等音等同关系（见谱10）。以商为轴进行十二音序列倒影，实现原型序列中的一宫一均在倒影序列中不变，实现了极大值不变性。

较《牵牛花》早两年发表的艺术歌曲《涉江采芙蓉》⑭［唐］李白诗、罗忠镕曲：《涉江采芙蓉》，《音乐创作》1980 年第3 期，第53 页。，是新中国成立以来歌曲创作领域使用十二音序列技术的标志性作品。“思远道……望旧乡”，罗忠镕用十二音矩阵空间上的序列变换，点化了诗词上阕与下阕之间的空间转换。取“回望”之意，曲作者充分而又经济地利用原型序列P6及其逆行序列R2，洋洋洒洒地贯穿了整个上阕。尔后，作者又巧妙地利用原型序列的倒影I6及逆行倒影RI10完成下阕。如谱11所示，由于采用了作为商音的♯F（E 宫系统）为轴进行原型—倒影序列变换，变换后的倒影序列I6在变换过程中完全复现了P6的宫系统结构——E 宫五声+♭E 均七声（不计第20 小节“长”字所对应的♭E 音）。利用商轴倒影实现变换中极大值不变性宫系，使得变换前后的两个序列，P6和I6，虽有“原型”“倒影”形式之别，却似转非转，“离居而同心”，这样的呼应明白晓畅。

谱11 《涉江采芙蓉》（罗忠镕曲）五声性十二音序列原型P6与倒影I6（商=♯F，商轴）

1986 年春，榕城的西子湖畔，桃发红萼，鹂鸣翠柳，极目远眺，青草湖水相连，白鹭青天相印。这番家门口的春景深深地打动了一位福州籍作曲家的内心。彼时，时任福建省艺术研究所副研究员的郭祖荣得到了著名词作家林澍的合作邀请，用自由十二音技法创作出了一首民族风格浓郁的艺术歌曲《湖中雨意》⑮林澍词、郭祖荣曲：《湖中雨意》，《音乐创作》1988 年第1 期，第38 页。。为求突出中国化的旋律于十二音中，曲作者精心设计了一条至少包含了五种民族调式的原型序列P11。⑯P11：11，1，6，9，4，8，0，2，10，5，7，3。该原型序列起于A 宫五声（1—5 音），1—6 音为E 宫六声（带清角音）；7—11 音为♭B 宫五声，7—12 音为♭E 宫六声（带变宫音），♭A 均隐于其中（6—12 音）。为印证以商为轴可实现原型—倒影变换中宫系的极大值不变性，谱12 仅以五声+七声为法（A 宫五声+♭A 均七声）截断该五声性十二音。宫系频繁推移，彼此交叠。连续的调性变化，点化了虚无缥缈亦真亦幻的诗词意境，保持了词曲结合的有机联系。

谱12 《湖中雨意》（郭祖荣曲）再现段（第21—26 小节）五声性十二音序列原型P11宫系截断（人声声部）与倒影I11宫系截断（钢琴伴奏声部）

节选《湖中雨意》再现段，声乐部分再现了呈示段所使用的原型序列P11，而钢琴伴奏部分则使用了原型的倒影序列I11。由于起始音B为P11首宫A 之商音，以商为轴进行倒影变换后，倒影序列仍保持原型序列的五声性结构不变，实现了对原型序列上的一宫一均的全部保留。

初识序列，以为艰涩；含英咀华，意趣充然；玩味中西，慕然回首，方悟其中之妙。以商为轴的原型序列P11及其倒影序列I11的重叠，其实在前奏中早已并置在了一起（见谱13）。

谱13 《湖中雨意》前奏（第1—4 小节）五声性十二音序列原型P11与倒影I11宫系截断

相较于具有传统五声性调性音乐的旋律，《湖中雨意》的人声声部五声性调性因素刻意回避方整性的乐句结构，伴奏声部则凸显极端长时值音符和休止符以及建立在非常规节奏之上的超大跨度的旋律音程等“非钢琴化材料”。使用交响化写作技术体现音响结构多样性的同时，也表明了郭祖荣对传统调性音乐所采取的回避态度，试想摆脱调性音乐控制的决心逐渐明朗化。然，或隐或显地强调序列内部及其变换过程中A 宫五声—♭A 均七声这一对不变性材料，并将它们放置在歌曲的前奏及最后部分，则应被视为作曲家对传统五声性调性功能结构所作的辩证继承。

（二）宫角轴与倒影变换中的极大值不变性宫系

均隔4 个半音的三音集合3-12={0，4，8}（移 位{1，5，9}，{2，6，10}，{3，7，11}）可将12 音级钟均分为三等份，首尾接续，每一等份包含5 个音级。循此法，以C（0）—E（4）—♭A（8）为序列之龙骨框架，朱践耳先生为他的《第十交响曲》设计了一条由C 宫、E 宫和♭A 宫五声首尾咬合接续而成的十二音原型序列P0。以4 为移位值的三个宫系等分了12 个音级，两两宫系之间均交叠有一个不变音级。⑰音程向量［032140］决定了取d4=1 所对应的音程数，即以4（大三度音程）为T 值进行移位，五声音阶变换双方将存在一个共同音交集。如谱14 所示，序列起始于C 宫宫音，C 宫五声止于角音E，生E 宫之宫音，E 宫五声止于角音♯G，生♭A 之宫音（♯G=♭A），序列止于♭A 宫羽音F，续以序列首音C 为♭A 之角音，生C 宫之宫音……由此，十二音闭环，相邻两宫之不变音级宫角互换，三宫循环往复，生生不息。

谱14 朱践耳《第十交响曲》五声性十二音序列原型P0之三宫截断：p0—p4—p8，音程数数列现极大值不变性

传统民族五声调之间的关系可分为以核心调的宫音为轴向下属方向扩展和以角音为轴向属方向扩展。比如以C 宫五声为核心调，以宫音C 为轴作倒影变换，可生♭B 宫五声、♭A 宫五声、F 宫五声以及♭E 宫五声，核心调C 宫与其派生宫系♭A 宫之间，宫角互换；以C 宫五声为核心调，以角音E 为轴作倒影变换，可依次产生A 宫五声、G 宫五声、E 宫五声以及D 宫五声，核心调C 宫与其倒影派生宫系E 宫之间，宫角互换。

以不变音级C、E、♯G为轴， 得五声性音级集合矩阵三个，Penp0·i0、Penp8·i8和Penp4·i4，⑱大写字母“P”“I”用以标识十二音序列原型与倒影，小写字母“p”“i”用以标识五声序列原型与倒影。将它们作首尾接续有机复合在一起。图1 展示了《第十交响曲》五声性序列p0（源）—p4（路径）—p8（目标）之“Z”字形移位派生路径。

进一步的，当P0=р0+р4+р8，则有P4=р4+р8+р0和P8=р8+р0+р4。所以，当 有P0-P4-P8作循环移位时，三宫宫系循环交替出现：C 宫-E宫-♭A；E 宫-♭A 宫-C 宫；♭A 宫-C 宫-E 宫，实现了原型序列移位变换中的极大值不变性宫系。

由于十二音原型序列P0中最明显的不变量是三个五声音列中对“+2,+5,+2,-7”音程数数列的保留，所以，十二音序列矩阵FP0·I0⑲图2 采用了十三音矩阵是为了能在二维平面中完整地表示三个宫系统。实则第13 行与第1 行重合，第13 列与第1 列重合。可被分割为三种等价的分块五音矩阵Penp0·i0、Penp8·i8和Penp4·i4，纵横共计9个。它们分别以0 （C宫宫音）、4（E 宫宫音）和8（♭A 宫宫音）为轴进行倒影变换。以图2 为例，循倒影变换后宫角互换之理，Penp0·i0中的p0经宫轴倒影后得i0（♭A 宫五声），Penp8·i8中的p8经宫轴倒影后得i8（E 宫五声），Penp4·i4中的p4经宫轴倒影后得i4（C 宫五声）。

进一步的，当I0=i0+i8+i4，且i0=p8、i8=p4、i4=p0，则I0=р8+р4+р0，I0=RP0，实现了十二音原型序列P0与倒影序列I0之倒影变换中极大值不变性宫系。

图1 宫角轴与五声性序列矩阵中的 p0—p4—p8 之移位派生

图2 《第十交响曲》十二音序列矩阵FP0·I0 之 分块矩阵Penp0·i0 、Penp8·i8 和Penp4·i4

谱15 《第十交响曲》十二音原型序列P0与倒影序列I0之倒影变换中宫系邻接不变量

在音高元素迁移的过程中，作曲家巧妙地设置以宫角为边界音，以4 为移位值，建立起了新的且十分稳定可靠的逻辑关系，促成了倒影变换中，横向宫系邻接、宫系内部音程数列等两个不变量，且促使三个宫系联系为息息相关的一个整体。三者之间相互包容、互为因果，没有一个可以离开其它两个而独存。三者之间仅存在一种不可分割的本质和属性，即对称循环，驱使音乐深层结构的简约与稳定。“在音乐中，形式不能脱离逻辑，而逻辑必须保持统一性。”⑳［美］唐纳德·杰·格劳特、克劳德·帕利斯卡：《西方音乐史》，汪启璋、吴佩华、顾连理译，北京：人民音乐出版社1996 年版，第756 页。通过建立不变量，原型序列及其倒影变形在时间的运动中完成音高迁移的同时，两者实为一体且始终保持着统一的逻辑，完成了该主题的一体化写作，实现了“移步不换形”的艺术效果。

三、小于极大值不变性与五声性 十二音序列的变换网络

（一）移位值与十二音序列五声性截断移位变换中的小于极大值不变性

在芦世林为科教影片《丹顶鹤的一家》配乐的一些十二音序列音乐段落中，比如《前奏曲》的序列原型P7，如图3 所示，该序列上至少交叠有四种五声宫系——G 宫、B 宫、♭A 宫还有♯F 宫。其中，除了宫音以1 或11 为移位值的五声宫系G 宫和♭A 宫间无共同音保留之外，宫音以5 为移位值的B 宫系和♯F 宫系之间保持的共同音为至多（4 个），实现了3 个音高邻接不变；次之是以2 为移位值的♯F、♭A 二宫，保持共同音3 个，实现了2 个音高邻接不变；以3 为移位值的B、♭A 二宫，保持共同音2 个，实现了1 个音高邻接不变；至少也有1 个共同音的是以4 为移位值的G、B 二宫。

图3 芦世林《前奏曲》十二音序列原型P7 之五声性 截断的变换音网，不变音级，音高邻接不变量

从图4 的五声性截断的变换音网可以看出，与保持至多3 个音高邻接数量不变相联系的多重宫系移位变换完成了《溪声》的十二音序列原型P4。居于序列中间位置的以5 为移位值的♭B 宫和♭E 宫之间保持了4 个共同音，实现了3个音高邻接不变；次之是序列两端的以3 为移位值的G、♭B 二宫和♭E、♭G 二宫，分别保持了2 个共同音，实现了1 个音高邻接不变。

图4 《溪声》十二音序列原型P4 之五声性 截断的变换音网，不变音级，音高邻接不变量

在这里，移位值是不变量的生成机制，移位值的选择关乎不变音级或音高邻接的数量，也是调性因素频繁推移的成因。最大限度利用调性因素的频繁推移来加强序列内部动力发展。十二音序列内部这些与五声性截断相对应的宫系之间，以更多的共同音自然过渡，互相具有1 至4 个不等的共同音，使得一个宫系向另一个宫系的过渡几乎察觉不到。每一个瞬间是它自身，但同时又是别的什么——一个宫系还未走到尽头，另一个宫系却已悄然萌芽，开始了一场踏旧路而自辟蹊径的行程。它们色彩不同，自具个性，却又和谐地构成一个有机统一的十二音序列体系。从变换的规则式构图到音响的自然式构图，整个十二音序列都建立在五声旋法的支架之上，音程序进流畅，音调风格统一连贯，宛如一条分布均匀、过渡自然的“小溪”，层层跌宕，峰回路转，新意不绝，悦耳不绝，并且在溪水中能看到五光十色、变换无穷的景致。

（二）宫角轴与倒影变换中的小于极大值不变性宫系

为迁就五声性十二音序列内部多重宫系的频繁推移与堆叠，势必导致各宫系无法保证都能以其宫角音为边界音，各宫系五声音阶的音程序进也无法统一，也就无法实现倒影变换中对原型序列所有宫系的保留。以《前奏曲》为例，虽有以G 宫宫音为轴进行倒影，倒影序列I7中也仅保留了原型序列P7中的B 宫五声，新赋♭E宫、E 宫和D 宫。《溪声》因以G 宫羽音E 为轴，故I4仅保留了P4中的两个宫系不变，即♭B、♭G二宫，新赋♭D 宫、A 宫。此外，除倒影轴音E，音级♭B 在原型和倒影序列中的音序位置保持不变。

谱16 《前奏曲》十二音原型序列P7与倒影序列I7之倒影变换中小于极大值不变性宫系

谱17 《溪声》十二音原型序列P4与倒影序列I4之倒影变换中小于极大值不变性宫系

不变性宫系的数量视倒影变换中每一个环节的机制问题，不断变化的宫系具有多样统一的形式美感。通过对小于极大值不变性宫系的观察，笔者发现了两个有意思的现象：1.作为在倒影变换过程中始终具有不变性的宫系，则具有中心宫系的地位。以《前奏曲》为例，如谱16 所示，十二音序列P7与其倒影序列I7中的5 个音（B 宫五声）保持在原位，除轴音外的6 个音作了左右换位，其中部分音是等音变化。2.《溪声》的十二音序列因宫系堆叠而出现了的共同音，共同音的数量呈2—4—2 中心对称。至此，笔者不禁追问，生成上述现象的机制又是什么呢？

（三）均控框架、音轴与五声性十二音序列

我们通常把相邻音级间无半音和三全音，其3 至5 音截断具有五声性音调特征的序列称为“五声性的十二音序列”。㉑郑英烈：《十二音技法在中国作品中的运用》，《音乐研究》1986 年第1 期，第24 页。诚然，五声性十二音序列的截断方式是多样性的，笔者在前文中结合不变量的产生机制，论述了五声性十二音序列的多种结构形态，以作为创作具有鲜明特色的中国风格序列之作曲规则。而在这些规则与现象的背后，中国传统乐理学理论中“均”以及“均”的组合所形成的的十二音框架，即“均控框架”，是五声性序列得以生成之决定性机制。

以五度相生为法，五度链的7 音截断可构成一均，8 音截断可构成两均，9 音截断为三均，以此类推，12 音一般可构成6 均。相邻两均不变音级为至多（6 个），隔一均共同音减至5 个，12 音序列的外缘两均，因对“均控框架”有支撑作用，所以称之“基均”或“两基均”。两基均之间共同音只有两个，是十二音序列中居中的两个音级，称其为“音轴”。

1．双音音轴（不变音级）与两基均均控框架

《牵牛花》《溪声》等序列都是五声性十二音序列（如前文中谱2 所示），都是源于两基均和双音音轴的框架。由相隔半音的外缘两均，F 均和♭G 均构成的均控框架，两均之共同音（音轴）为居于序列中心的6—7 音，一个纯四/五度音程。循同均三宫之理，音轴前是F 均之G 宫五声截断，音轴后是♭G 均之♭G 宫五声截断，前呼后应连为一体，互补为五声性十二音序列。在音轴的前后，《溪声》序列中还隐伏着其它不完整的、无法确定的均（见谱18）。正是叠均的不完整性，使得那些无法完全归属均控框架的五声音阶具有更为“暧昧”的立场，导致宫系堆叠不变音级增多。倒影变换中作为不变性宫系被保留的也通常是那些不属于均控框架的五声。《溪声》不仅有音轴二音作为两基均变换之间的不变量，不变量同样也反映在音程序列上。如谱18 所示，以双音为轴，作曲家设置该序列两端的五声性音列倒影同构，以保证“-7,+2,+3,-7,-2”这一音程数序列不变（逆行相同）。这一数列作为一个恒定的向量，因作曲家所设定的五声音组划分不与歌词断句、小节线或拍号所规定的强弱规律吻合，故而，在音高迁移过程中，守恒的opi 数列结构所在的五声性截断既能独立于人们所期待的强弱规律之上，又让十二音序列不失内在逻辑的整体性和稳定性。

谱18 《溪声》五声性十二音序列原型均控框架与音轴（不变音级）、音程数量不变量

芦世林的《前奏曲》序列是两基均上叠一均的框架结构，以♯C—♯F 为音轴，音轴前是G均之G 宫五声，音轴后是♯F 均之♯F 宫五声和♯G 宫五声（♭A 宫五声）。除双音音轴在两基均变换过程中保持不变外，相隔纯五度的B 均和♯F 均在变换过程中则保持了6 个音级不变。

谱19 《前奏曲》五声性十二音序列原型均控框架与音轴、均场变换与不变音级

2．四音音轴（不变音级）与两基均上叠两均的均控框架

如前文所述，五度链的十二音序列，两基均框架之上，至多可以叠四均，可构成两均的8音截断，保持的共同音为至多（6 个）。对照朱践耳《第十交响曲》序列原型，该序列框架主要是由两基均控制，上叠两均。在C、B 两基均和上叠G、E 两均中，共计有4 个不变音级（见谱20a）。四音音轴，以奉五声——E—B—♯F—♯C 为顺向五度链。由于C 均—G 均、E 均—B均这两对均场相隔纯五度音程，故而在变换过程中，这两对均场各保持了6 个音级不变，实现了小于极大值不变性（见谱20b）。

谱20a 《第十交响曲》五声性十二音序列原型均控框架与音轴（不变音级）

谱20b 《第十交响曲》五声性十二音序列原型均场变换与不变音级

3．极点为轴（不变音级）与两基均均控框架

《涉江采芙蓉》和《月下独酌》也是两基均均控框架。但这两个序列的均框架轴音并非居于序列正中的6—7 音，而是第6 音和第12 音。以《涉》为例，我们将谱21 所示序列首尾接续环形成十二音级钟（见图5），便可直观地看出所谓轴音正好位于环形直径两端，D、♭E 两基均以极点音D、A 为轴。轴心的位置发生变化，并不影响两基均仍然以半音音程为距，在均场变换中所保持的两个不变音级，即轴心音，其音程关系还是纯五度。

谱21 《涉江采芙蓉》五声性十二音序列原型均场框架与音轴

图5 《涉江采芙蓉》五声性十二音序列原型 均场框架与极点音轴示意图

谱22 《月下独酌》五声性十二音序列原型均场框架与音轴

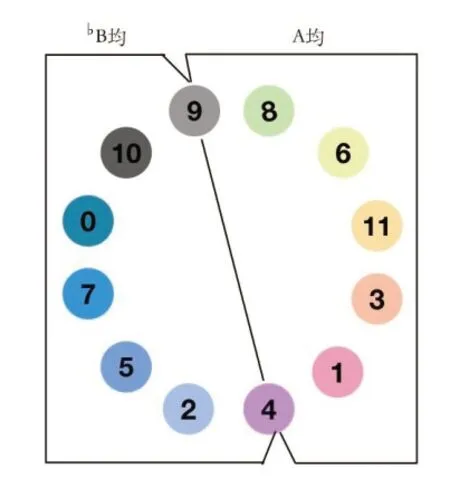
图6 《月下独酌》五声性十二音序列原型 均场框架与极点音轴示意图

进一步地，我们将《涉江采芙蓉》主题二均变换之下的两个不变音级D、A 置于半音序进的十二音级钟内，取D（2）-A（9）平行相关的5 组二音对子：{F（5），♯F（6）}，{E（4），G（7）}，{♭E（3），♯G（8）}，{♯C（1），♭B（10）}，{C（0），B（11）}。我们发现这6 组二音对子及其平行关系在《涉》的十二音序列主题中保持不变。

图7 6 组二音对子极大值不变性：从半音十二音级钟到《涉江采芙蓉》原型序列十二音级钟

结 语

借鉴一种产生于外域的律制，一种远离我们民族传统的现代技法，使十二平均律与五度相生律共生，十二音技法与五声旋法共存。从五声性十二音写法本身来看，作曲家在无调性思维中渗入了浓烈的调性因素。他们有意调和无调性思维的调性化和调性思维的无调性化，使这两个方面互相接近来达到十二音语言民族化的目的。㉒王宁一：《评科教影片〈丹顶鹤的一家〉中的序列音乐》，《乐府新声》1984 年第2 期，第48 页。诸多成功的实践证明，五声性十二音技法已经将新的原则与传统调性原则相熔化，熔诸多手法为一炉。在努力寻求有机联系的可能性和塑造形式美的同时，这些作品又肩负起反映历史、反映思想性，主张内容和形式、情与理的辩证统一的美学原则。