连续单调不减函数迭代产生的数列的收敛性

成凯歌

连续单调不减函数迭代产生的数列的收敛性

成凯歌

（浙江旅游职业学院 基础部，浙江 杭州 311231）

函数迭代是函数运算的重要内容，也是反映重复运动的重要数学模型，函数迭代产生的结果和函数本身的性质密切相关，越是复杂的函数迭代后往往会产生越复杂的结果，所以，函数迭代研究通常从简单函数开始．单调连续函数作为一类较简单的函数，它的迭代一直是迭代研究的重点内容之一，对定义在有限闭区间和无限区间上连续单调不减函数的迭代产生的数列进行讨论，证明了定义在有限闭区间上连续单调不减函数在定义域中任意一点的迭代产生的数列都收敛，给出了定义在无限区间上连续单调不减函数迭代产生的数列的收敛条件．

连续单调不减函数；迭代；数列；不动点；收敛

1 引言及预备知识

迭代是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果，每一次对过程的重复称为一次迭代，而每一次迭代得到的结果会作为下一次迭代的初始值．迭代是自然界和人类社会的一种常见普遍现象．从数学的角度看，迭代就是重复执行一系列运算，从前面的量依次求出后面量的过程，此过程的每一次结果，都是由对前一次所得结果施行相同的运算步骤得到的.

关于映射迭代的研究，较早的数学家有E.Schröder[1]，N.H.Abel[2]，J.M.Dubbey[3]．近代以来，随着自然科学的进一步发展，对迭代的研究提出更多更高的要求，并且促进了迭代方程的的发展.

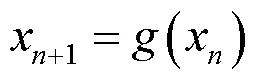
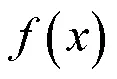
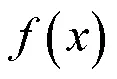
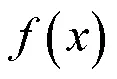
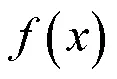
引理4[16]单调有界数列必有极限．

2 主要结果及证明

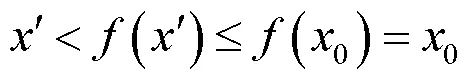
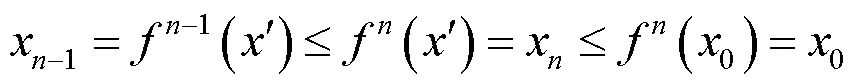
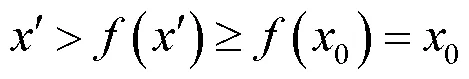
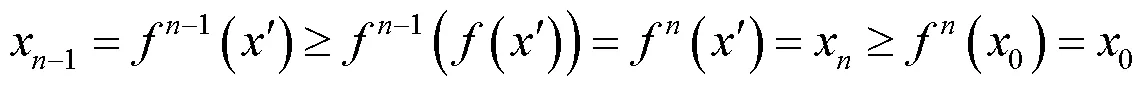
证明 情况（1）的证明类似于定理1证明中的（ii）； 情况（2）的证明类似于定理1证明中的（iii）.

（4）其证明和定理2中的情况（3）和情况（4）的证明完全类似. 证毕．

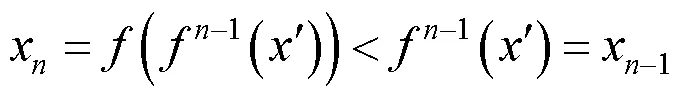
（3）其证明和定理2中的情况（3）和情况（4）的证明完全类似. 证毕．

3 结语

函数的迭代会产生许多意想不到的结果，对于复杂的函数，其迭代会更为复杂．本文按定义域是有限区间和无限区间，分别对连续单调不减自映射的迭代进行了讨论，得到其迭代产生的数列的收敛或者发散的情况．如果收敛，一定收敛到这个自映射的不动点；如果发散，则一定是无穷大量. 后续将进一步研究连续单调不增函数、连续非单调函数和非连续函数迭代产生的数列的收敛情况.

[1] Schröder E．Überiterate funktionen[J]．Math Ann，1871，3：295-322．

[2] Abel N H．Oeuvres completes[J]．Christiana，1881，2：36-39．

[3] Dubbey J M．The Mathematical Work of Charles Babbage[M]．New York：Cambridge University Press，1978：13-64．

[4] 陈伟军．一类平顶单峰映射的迭代[J]．四川师范大学学报（自然科学版），2015，38（3）：391-397．

[5] 刘晓华，罗天琦．迭代运算使不连续映射变为光滑映射[J]．西南大学学报（自然科学版），2021，43（8）：84-92．

[6] 陈荔靖．一类含迭代的二元均值函数[J]．四川大学学报（自然科学版），2020，57（6）：1033-1037．

[7] 王宇翔．一类压缩型映射的不动点定理[J]．大学数学，2021，37（1）：1-4．

[8] 龙爱芳．避免导数计算的一个新的迭代公式[J]．大学数学，2017，33（2）：108-110

[10] 刘晓华，罗世超．有理函数的迭代[J]．乐山师范学院学报，2020，35（4）：1-5．

[12] 同济大学数学系．高等数学：上[M]．7版．北京：高等教育出版社，2014：7-8．

[13] 邱森．高等数学基础：上[M]．2版．北京：高等教育出版社，2018：58-63．

[14] 程其襄，张奠宙，胡善文，等．实变函数与泛函分析基础[M]．4版．北京：高等教育出版社，2019：135-136．

[15] 俞建，贾文生．不动点与平衡点[J]．运筹学学报，2020，24（2）：14-22．

[16] 华东师范大学数学系．数学分析：上[M]．4版．北京：高等教育出版社，2010：36-39．

Convergence of the number sequence generated by iterations of the continuous and monotone-non-decreasing function

CHENG Kaige

（Department of Basis Course，Tourism College of Zhejiang，Hangzhou 311231，China）

The functional iteration is the important contents of function operation and an important mathematical model reflecting the repeated movement．The results of functional iteration are closely related to the nature of the function itself，the more complex results of iteration are produced by the more complex functions，thus，the researches of the functional iteration are usually began from the simple functions．The monotonic and continuous functions are considered as a simpler class of functions，its iterations are thought as one of the important issues of iterative research.By discussing the number sequence generated by iterations of the continuous and monotone-non-decreasing function defined on the finite closed interval or the infinite interval，it was obtained that the number sequence generated by iterations of the continuous and monotone-non-decreasing function defined on the finite closed interval is convergence at any point in domain，and the conditions of the convergence of the number sequence generated by iterations of the continuous and monotone-non-decreasing function defined on the infinite interval was given.

continuous and monotone-non-decreasing function；iteration；number sequence；fixed point；convergence

O192

A

10.3969/j.issn.1007-9831.2022.02.001

1007-9831（2022）02-0001-06

2021-09-03

浙江旅游职业学院优质课程资助项目（2017ZLY012）

成凯歌（1968-），男，浙江杭州人，讲师，从事函数研究．E-mail：zjchengkaige@sina. com