基于CEEMD和LSTM-ARIMA的短期风速预测

李秉晨， 于惠钧， 丁华轩， 刘靖宇

(湖南工业大学轨道交通学院，湖南 株洲 412007)

0 引 言

风能作为理想的可再生能源之一，在世界各国的应用都越来越广泛，但风速本身具有随机性和间歇性的特点，会使风电出现频繁的波动，在进行大规模风电并网时，会对电网的正常运行和电能质量带来威胁[1]。因此，准确预测风速有利于风电并网的调度，对电力系统的稳定运行有重要作用[2]。

目前，风速预测受到很多国内外研究人员的关注，采用多种模型对风速进行预测。风速预测常用的方法包括卡尔曼滤波法、自回归差分平均回归、人工神经网络、支持向量机、经验模态分解（empirical mode decomposition，EMD）等[3]。单一模型在预测风速时，往往存在精度不高的问题，越来越多的研究人员开始研究组合模型[4]。文献[5]针对风速序列具有很强的波动性，提出基于VMD和ARIMA的超短期风速预测模型，利用改进经验模态分解算法将风速序列从高到低逐次分解，然后对各分量分别建立ARIMA模型进行预测，结果表明模态分解法在风速预测有较大优势。文献[6]利用局域均值分解法将风速序列分解为若干分量，再对各分量分别采用ARMA算法进行建模预测，提出LMD和ARMA组合风速预测方法，提高了风速的预测精度。文献[7]提出基于VMD和LSTM的超短期风速预测，用VMD将风速序列分解为多个子模态，对子模态进行预测并叠加得到预测结果。文献[8]提出基于CEEMD和改进时间序列模型的超短期风功率多步预测模型，CEEMD算法在经验模态分解算法上进行改进，能更好地将非线性时间序列分解为代表不同时间尺度上的局部特征的模态分量，能提高风速预测精度。

以上模型都考虑了将风速序列分解为不同频率的高低频模态分量，然后分别对高频和低频分量建立预测模型进行风速预测，但是没有考虑算法对不同频率子模态的适用性，只是采用同一种算法对高频和低频模态分量进行预测。本文在现有研究的基础上，提出基于CEEMD和LSTM-ARIMA的短期风速组合预测模型，ARIMA模型对于低频的平稳时间序列预测结果精确，而LSTM神经网络能对高频的非平稳时间序列取得较好的预测精度，采用CEEMD算法将LSTM与ARIMA模型结合起来，用LSTM网络和ARIMA算法对经CEEMD算法分解的高频和低频的模态分量分别进行预测，以期提高风速预测精度。

1 算法原理

1.1 CEEMD原理

经验模态分解算法(EMD)是一种常用于非平稳时间序列信号的数据处理方法，可将非平稳信号分解为一系列不同时间尺度的本征模态函数(IMF)分量，不过该方法存在模态混淆的现象。完备总体经验模态分解(CEEMD)算法在EMD算法的基础上进行改进，添加一组大小相等、符号相反的辅助白噪声，然后再分别进行EMD分解，既抑制了EMD算法的模态混淆效应这一缺陷，又不会使得原始信号因白噪声的添加而产生较大的影响。CEEMD主要步骤如下[9]：

1）在原始的序列x(t)中，添加一组符号相反的高斯白噪声εi(t)序列，得到一组新的时间序列：

2）对式（1）中的每一个时间序列进行EMD分解，都会得到m个本征模态分量：

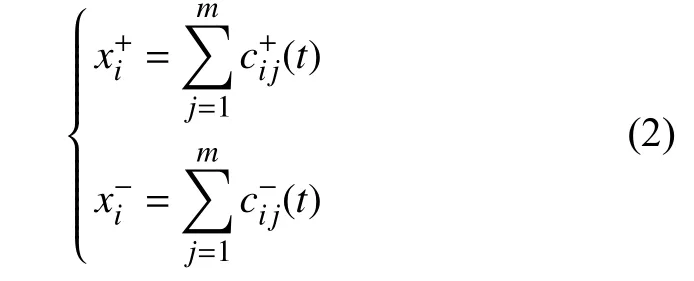
其中cij为第i次加入白噪声后，经过EMD分解得到的第j个模态分量。

3）添加不同的高斯白噪声，重复步骤1）、2）分别n次，得到n组本征模态分量(IMF)的集合，其中最后一组为趋势项(Res)。

4）计算所有分量的集合平均值，得到最终的模态分量组ci(t)。

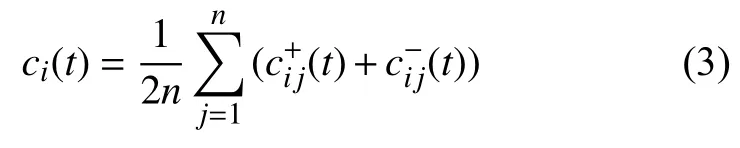
1.2 PE算法

排列熵(PE)算法是一种基于信息论的度量方法，通过相邻值的比较来分析时间序列数据的复杂性。PE算法的计算方法如下：

首先，假设一个时间序列X(t)(t=1,2,···,T)，对其进行相空间重构：

式中：m—— 嵌入维数；

τ 时间延迟。

然后，将X(t)中的元素按递增顺序重新排列：

其中jm为排序后各元素的序号。

每种可能的排列表示为w={j1,j2,···,jm},m维序列可以存在m!种排列方式。每种排列的概率为p1,p2,···,pg。根据 Shannon 熵定义，排列熵归一化可定义为：

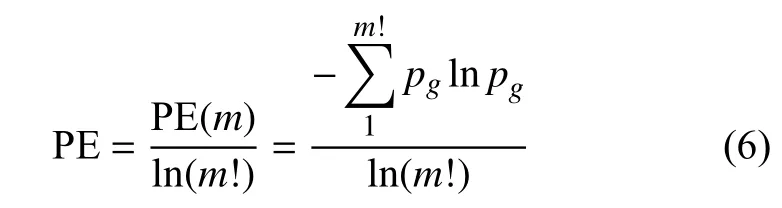
1.3 LSTM算法

长短期记忆网络(LSTM)是在循环神经网络(RNN)的基础上进行改进的算法，LSTM模型能有效地自动从时间序列数据中学习特征，并且能够学习长期依赖信息，避免了RNN训练过程中存在的梯度爆炸和梯度消失的问题[10]。与RNN不同的是，LSTM模型通过独特的门结构来增加一个细胞状态，用来保存以前的数据状态信息。LSTM模型结构如图1所示，单元内部结构由输入门、遗忘门和输出门等组成，此外，tanh激活函数控制要更新输入，Ct–1和Ct分别为t–1 和t时刻的细胞状态，ht–1和ht分别为t–1和t时刻细胞的隐藏状态。

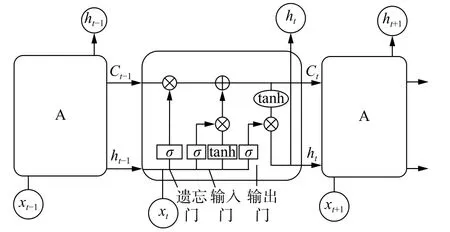
图1 LSTM模型结构图

LSTM模型的遗忘门用来确定t–1时刻的隐藏状态ht–1和t时刻的输入xt的信息保留程度。遗忘门的公式为：

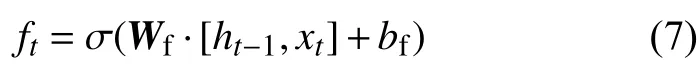
式中：W——f— 遗忘门的权重矩阵；

bf—遗忘门的偏置项；

σ 激活函数sigmoid。

LSTM模型的输入门用来确定输入变量xt中有多少信息可以保存到细胞状态Ct中。输入门的公式为：

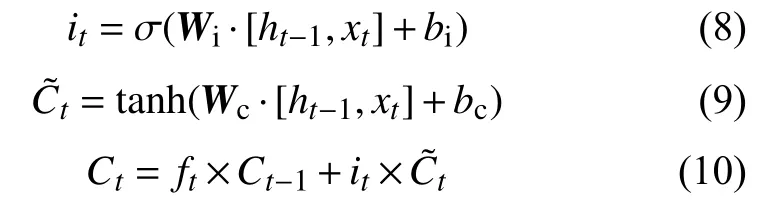
式中：Wi和Wc— 输入门的权重矩阵；

在两组实验对象入组后,于次日在空腹状态下抽取其外周静脉血(3毫升)和动脉血(2毫升),采取ELISA法(酶联吸附法)测定其IL—6、TNF—α水平,采取散射免疫比浊法测定其Hs—CRP水平,采取免疫发光法测定其BNP水平。本次实验所用IL—6、TNF—α试剂盒为北京伯乐生命科学发展有限公司生产,IMMAGE全自动特定蛋白分析仪和AU5800全自动生化分析仪为贝克曼库尔特公司生产。

bi和bc——输入的偏置项；

σ和tanh 激活函数。

LSTM模型的输出门用来输出单元的隐藏状态。输出门的公式为：

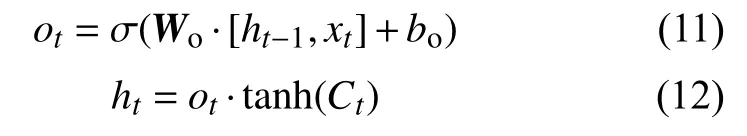
式中：ot—— —输出门的输出；

W——o输出门的权重矩阵；

bo输出门的偏置项。

1.4 ARIMA模型

自回归差分移动平均(ARIMA)是一种分析预测变量的未来值和历史值的线性函数关系的方法，ARIMA应用的时间序列应该是线性且平稳的。ARIMA(p,d,q)模型先对时间序列进行平稳性检验，如果不满足平稳性的要求，对时间序列进行d阶差分，然后再对序列进行自回归移动平均(ARMA(p,q))建模[11]。ARMA方程为：

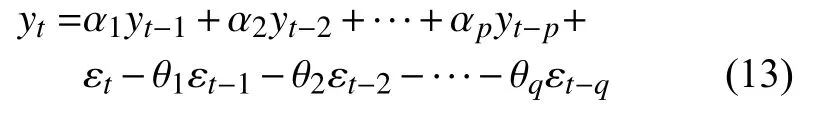
式中：yt——实际时间序列；

εt———t时刻的随机误差；

αp——自回归(AR)模型的系数；

θq移动平均(MA)模型的系数。

p和q都是模型的阶数，当q=0时，模型就简化为p阶AR模型AR(p)、当p=0时，模型就简化为q阶MA模型MA(q)。

2 基于CEEMD和LSTM-ARIMA组合预测模型

风速数据具有很强的非线性和非平稳性，采用CEEMD算法将功率序列分解为几个不同频率的子序列，采用PE对子序列进行计算，按照时间序列复杂度来选出高频子序列部分和低频子序列部分[12]。经CEEMD分解后的高频子序列部分使用LSTM进行预测，LSTM神经网络能对复杂度较高的时间序列进行有效预测；对于低频子序列部分使用ARIMA进行预测，ARIMA对于平稳的时间序列有良好的预测效果。将两种模型得出的预测结果进行叠加，最终得到风速的预测值。提出的基于CEEMD和LSTM-ARIMA短期风速预测模型建模步骤为：

1）利用CEEMD将原始风速序列分解为n个模态分量。

2）使用PE算法分别计算n个序列分量的排列熵，按照时间序列的复杂程度将模态分量分为高频部分和低频部分。

3）高频序列部分采用LSTM进行预测，低频序列部分采用ARIMA进行预测。

4）将高频序列预测结果和低频序列预测结果相加，得到风速的预测值。风速预测框图如图2所示。

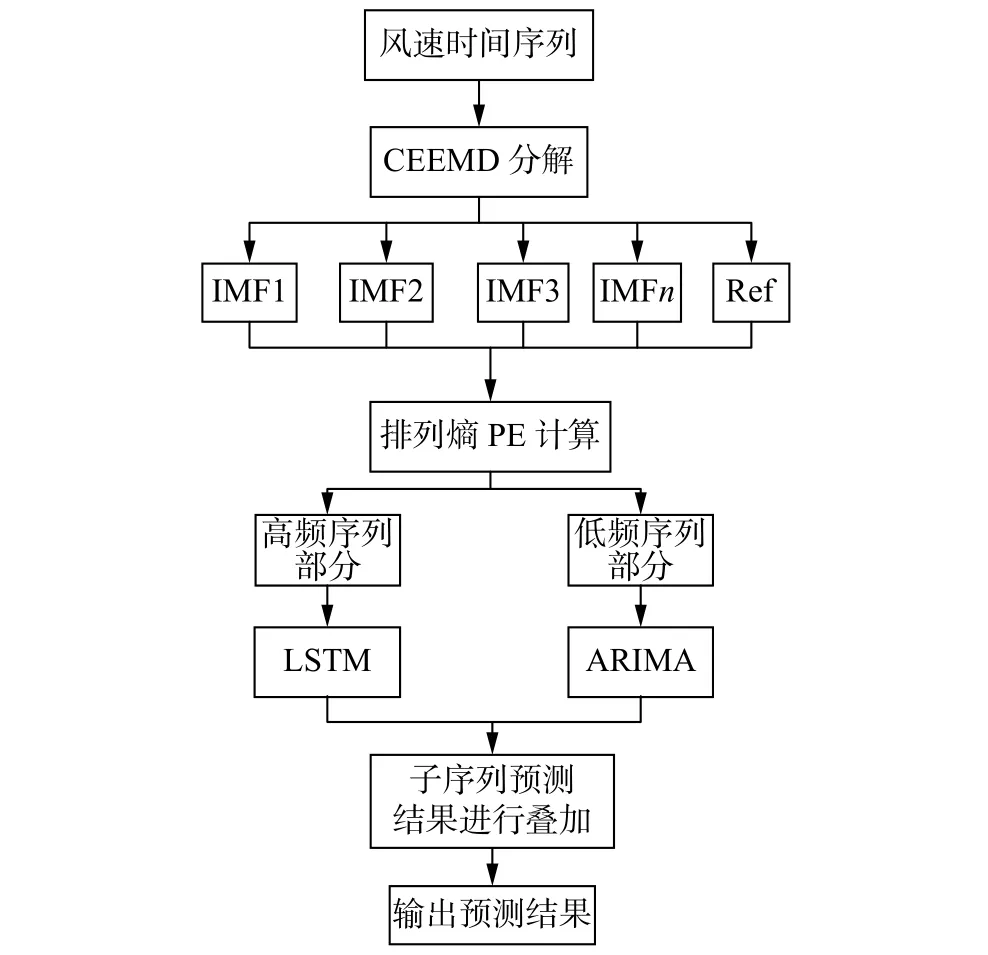
图2 风速预测框图

采用平均绝对百分比误差(MAPE)和均方根误差(RMSE)等性能指标来比较模型之间的预测性能水平。公式如下：

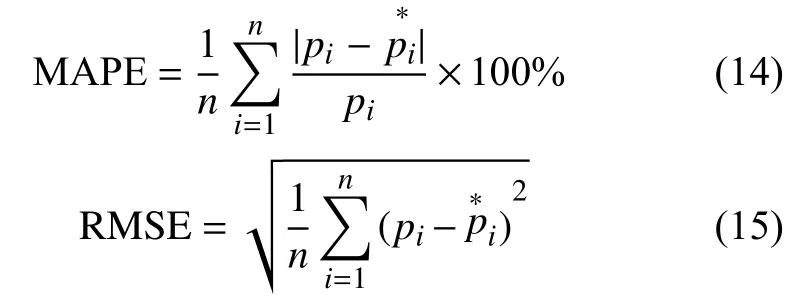
其中pi和分别为第i位的观测值和预测值。

3 算例分析

本文选用2016年湖南省某风电厂实际采集数据，样本的采样周期为5 min，选取4月10日～4月19日共2 880个点作为样本数据。原始风速数据如图3所示，其中前2 592个点(4月10日～4月18日)的数据作为训练样本（按8∶1划分训练集和验证集），后288个点(4月19日)的数据作为测试样本。

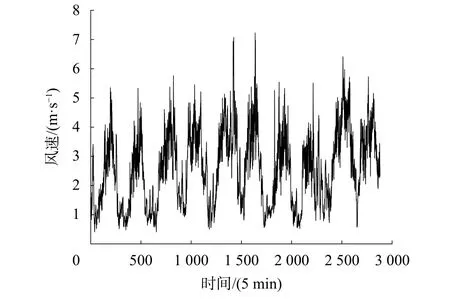
图3 原始风速数据

从图3可以看出风速数据具有明显的非线性和非平稳性，预测难度较大。对原始时间序列进行CEEMD分解，将风速分解为几个更容易预测的时间子序列，得到频率由高到低的11组模态函数。CEEMD分解结果如图4所示，可以看出IMF1至Res子序列的波动逐渐平缓，频率越来越低。

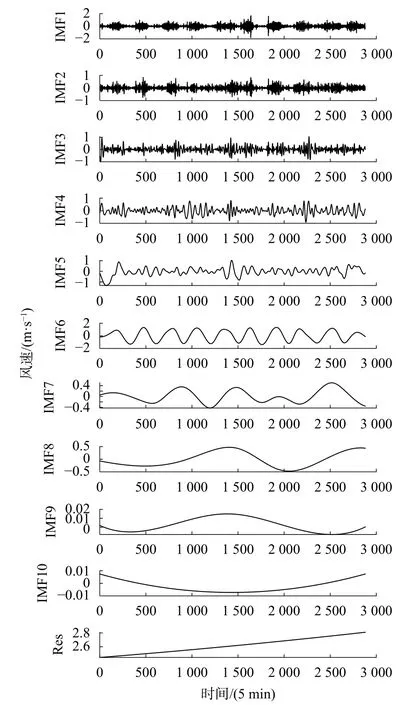
图4 CEEMD风速分解结果

为量化分解后各子序列的频率高低，采用PE算法计算各子序列的排列熵的值，具体结果如图5所示。排列熵值从IMF1开始依次递减，一直减到Res的排列熵值为0。对于ARIMA 模型来说，排列熵值越小，时间复杂度越低，模型的预测精度就越高。IMF5～IMF10及Res的子序列排列熵值均小于0.2，视为低频序列，带入ARIMA模型进行预测；IMF1～IMF4的排列熵值均大于0.2，将其视为高频序列，带入LSTM网络模型进行预测。

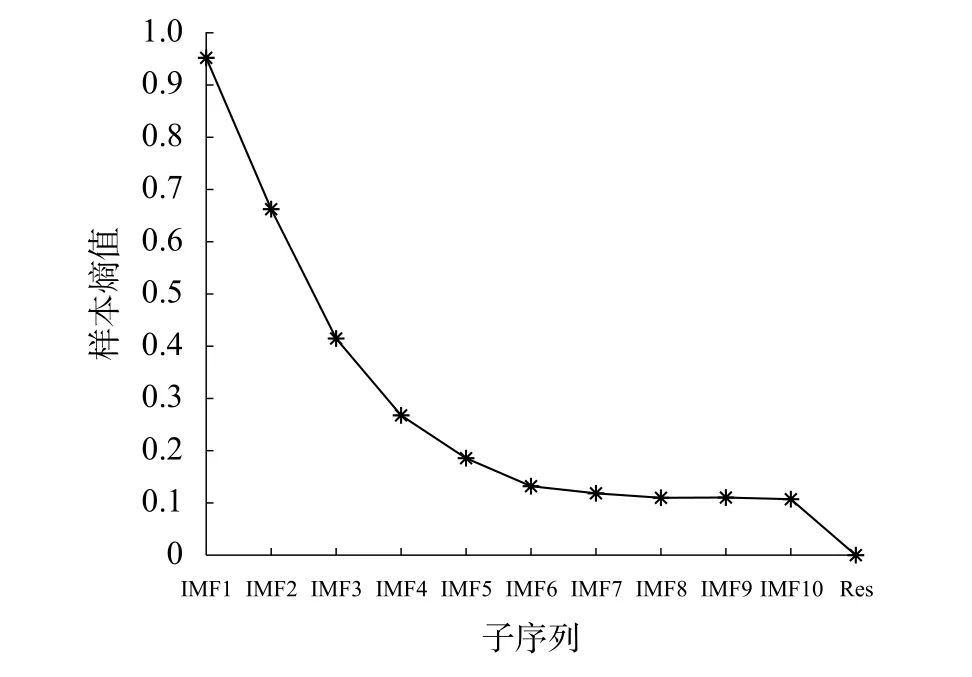
图5 子序列的排列熵结果

将CEEMD分解后的各子序列分量带入对应的算法进行预测，并将得到的预测值进行叠加，得到最终的风速预测数据。预测高频部分建立的LSTM模型参数为：单元数130，激活函数为relu，迭代次数150，余弦学习率下降。预测低频部分的ARIMA模型建立结果如表1所示。

表1 IMA模型阶数

为验证本模型对风速预测的有效性，与另外4种预测模型进行实验仿真对比。对比的预测模型分别为：LSTM神经网络预测模型、ARIMA预测模型和CEEMD-ARIMA预测模型。预测结果如图6所示，各模型预测误差比较如表2所示。

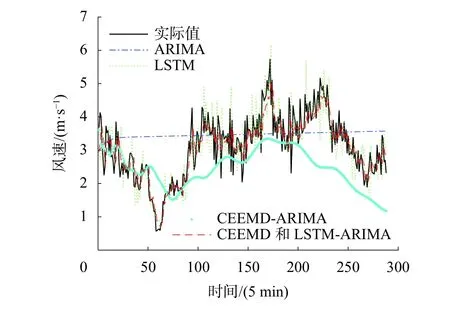
图6 CEEMD-LSTM-ARIMA预测结果以及其他模型对比

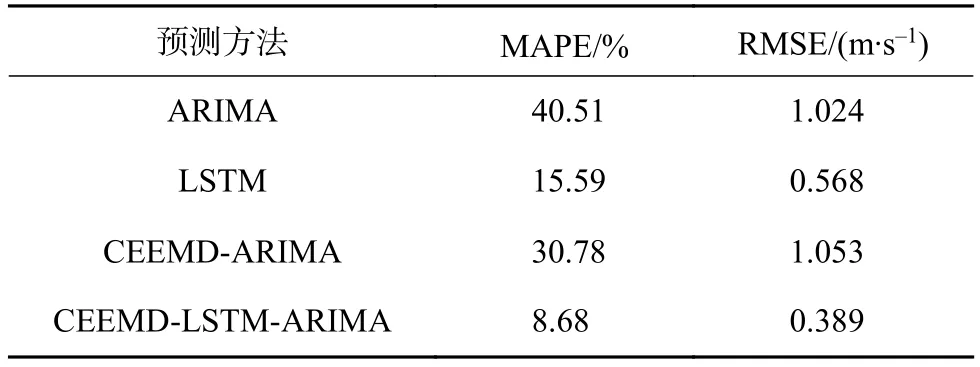
表2 各模型预测误差比较

由图6和表2可知，基于CEEMD和LSTMARIMA组合预测模型预测值与实际值最接近，MAPE为8.68%，比其他模型预测结果更精准。ARIMA模型预测近似一条直线，平均绝对误差达到40%，预测效果在所有模型中最差，说明单一的ARIMA模型无法对于风速这种波动大的非平稳数据进行有效的预测。CEEMD-ARIMA模型比ARIMA模型预测的平均绝对误差降低了10%，预测精度有所提高，说明CEEMD能有效对非平稳序列进行分解，提高了非平稳序列预测的精度。单一的LSTM模型预测精度较高，说明LSTM模型能对非平稳序列进行有效的预测，而基于CEEMD和LSTM-ARIMA组合模型比LSTM模型的预测误差更小，说明了组合预测模型的建模思路是正确的，消除各个时间尺度特征之间产生的相互影响，对各个模态分别进行有效的预测，进而提升整体的预测精度。根据结论可知，本文提出的基于CEEMD和LSTM-ARIMA组合预测模型可有效提高风速的预测准确度。

4 结束语

本文采用CEEMD算法将风速序列分解为不同频率的模态分量，达到降低了预测难度的目的。并分别采用LSTM和ARIMA模型对高频分量和低频分量进行预测，可实现对不同频率的模态分量进行有效预测，提高了整体预测精度。通过与其他模型进行对比，本文所提基于CEEMD和LSTM-ARIMA方法具有更高的预测精度，表明提出的组合预测模型是一种行之有效的方法。