蓝宝石超声高温传感参数技术研究

苗婉茹， 杨 录， 梁海坚， 陈 靖， 朱红伟， 王丙寅，迟 雪， 师钰璋， 李志玲， 王 高

(1.中北大学信息与通信工程学院，山西 太原 030051; 2.太原工业学院，山西 太原 030051;3.内蒙动力机械研究所，内蒙古 呼和浩特 010010)

0 引 言

超声温度测试技术广泛应用于航空航天、化工生产和军事等领域[1-3]。相比于传统热电偶和辐射测温传感器，超声温度传感器具有响应速度快、重复性好、精度高等优点，是一种具有广阔应用前景的新型温度传感器。在航空发动机温度测试中对传感器的温度测量范围、精度和灵敏度等特性参数有较高要求[4-5]。与传统传感器一样，超声温度传感器在使用前需要对其特性进行测试，以检验是否满足应用环境温度测量。

然而，目前国内超声温度传感器研制及测试技术研究相对较少。上海交通大学汪永为[6]等人通过蒙特卡洛法仿真测试传感器，实现精度优于1%。中国飞行试验研究院白雪等人对比PT100铂电阻温度传感器和光纤温度传感器测试结果，光纤温度传感器性能误差优于0.1%[7]。2018年中北大学[8]设计了一种铱铑合金超声导波测温系统，完成了该系统在高于1 000 ℃条件下的置信度评估。

本文在对超声温度传感器理论分析的基础上，搭建了超声温度传感器测试系统。在详细分析系统各组成部分的基础上，完成了自制蓝宝石超声温度传感器的测试，分析了灵敏度、重复性等特性参数，表明系统可有效解决超声温度传感器的测试问题。

1 测温理论

当不考虑边界条件时，固体材料作为各向同性传输介质，其内部的超声波传播速度可由材料密度、弹性模量和泊松比确定[9-11]。其中，材料密度与弹性模量是温度的函数。在固体材料中超声波传播速度可表示为：

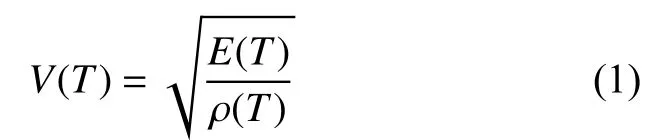
式中：E（T）—材料的弹性模量；

ρ(T)—介质密度；

T——环境温度。

基于此设计了一种超声温度传感器，传感器由波导杆和超声换能器组成[12]。声波沿着细线型波导杆传播，利用区截和端面的回波信号计算时间延迟，测量超声波的速度并获得材料的特性参数，通过测量声速即可获得被测环境的温度[13-14]。如图1所示为传感器结构图，超声在传感器中传播速度可表示为：

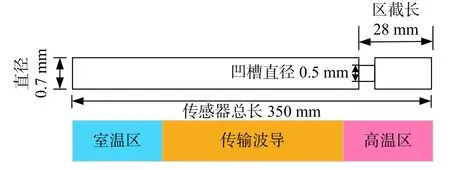
图1 传感器设计示意图

式中：L—区截长度；

Δt——回波信号时间延迟。

2 超声温度传感器测试系统

2.1 系统原理

测试系统主要由超声温度传感器、超声脉冲发射/接收系统、高温检定炉和计算机等组成。计算机控制超声脉冲发射/接收电路产生高压窄带电脉冲，通过超声换能器转化为超声波并作用于蓝宝石波导杆上，超声波传播到区截和端面处分别产生回波信号，超声换能器将回波信号转化为电信号后由计算机采集和处理。图2、图3分别为系统原理框图和测试系统示意图。

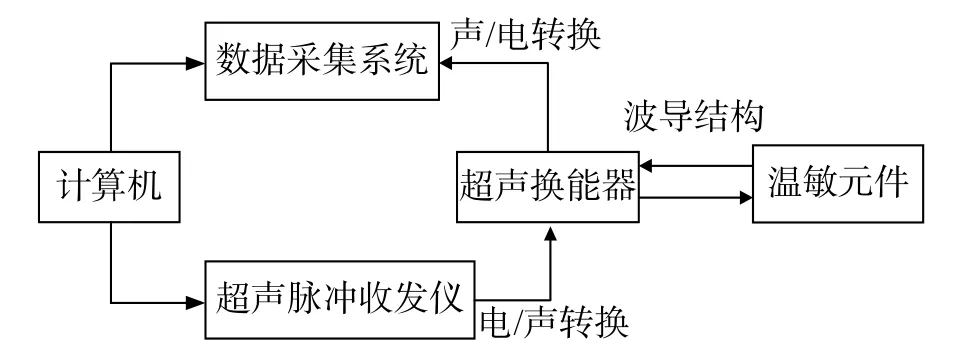
图2 测试系统原理框图

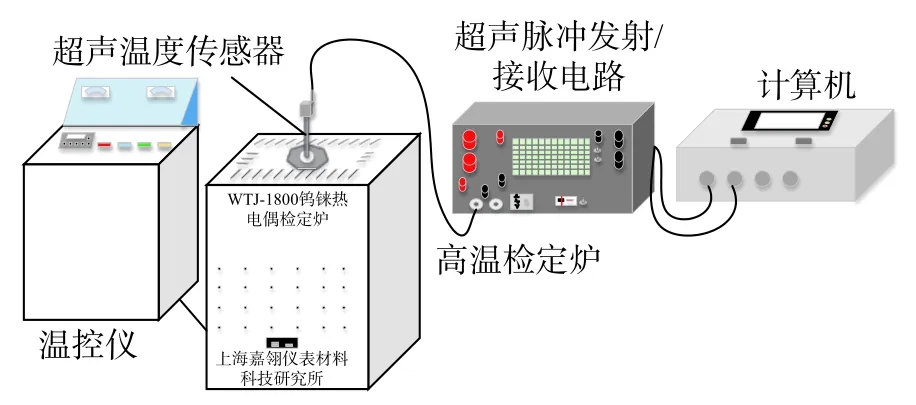
图3 测试系统示意图

2.2 高温检定炉

实验中使用高温立式检定炉对蓝宝石温度传感器进行测试。检定炉主要由硅钼棒、耐火砖、高温棉、高精度控温铂铑40-铂铑20热电偶和温控仪组成。研究在600～1 800 ℃温度范围内采用标准铂铑30-铂铑6热电偶置于与炉内高精度控温铂铑40-铂铑20热电偶相同位置处对检定炉内温度误差进行测试。其中标准铂铑30-铂铑6热电偶的测量不确定度为0.83 ℃。结果表明炉内高精度控温铂铑40-铂铑20热电偶测量不确定度为0.99 ℃，检定炉精度较高，可用于其他类型温度传感器测试。检定炉内温度测试结果如图4所示。

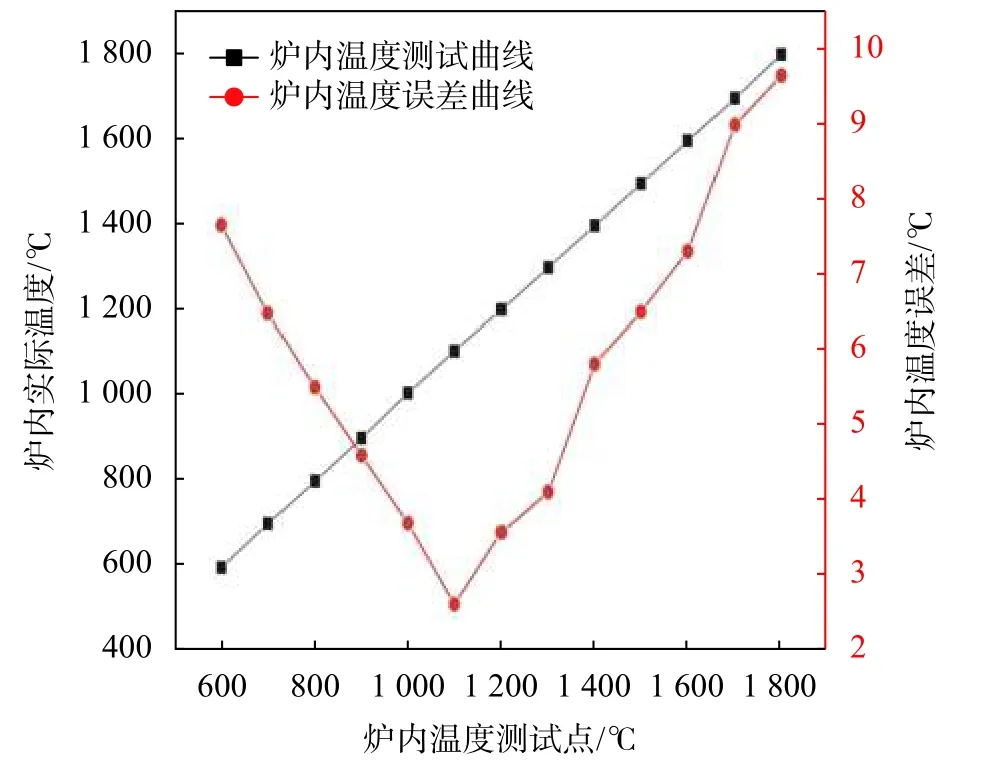
图4 检定炉测试曲线图

由图可知在1 100 ℃左右检定炉温度误差最小，此时1 min内热电动势波动最大为0.001 mV，该温度点的塞贝克系数为4.11 μV/℃，温度波动为0.24 ℃/min。选择30 cm处为恒温区中心，上下移动距离不超过2 cm，在此范围内监测温度波动。实验中同时将铂铑40-铂铑20热电偶敏感端与超声传感器的敏感区截置于炉内同一位置，热电偶显示温度即可作为超声温度传感器的参考温度。

2.3 计算机测试软件

研究采用美国国家仪器公司的超声数据采集系统LabVIEW软件，作为交互式界面与硬件系统配合。软件可实现单点测试、标定采集和接收显示超声信号等功能。设置采样频率为100 MHz。软件工作流程如图5所示。

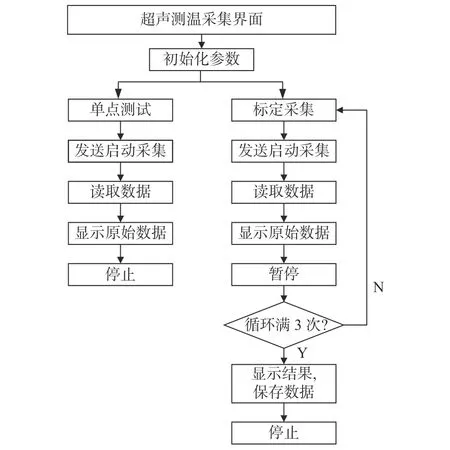
图5 软件工作流程图

3 蓝宝石温度传感器测试

传感器测试的主要目的是检测传感器的线性度、灵敏度、滞后性和重复性等特性参数是否满足应用环境温度测试要求[15-16]。

为了提高高温环境中声速测试结果的精度，测试过程中进行多次升温-降温循环[17]，实现对同一温度点处声速多次测量，取平均值作为该温度点处的超声传播速度。

3.1 时延估计算法

互相关（CC）算法是时延估计技术中最基本的信号处理方法，常用于比较两信号在时域上的相似程度[18]。通过以下两种信号分析模型来进行时延值的求解。假设输入信号为x1(t)和x2(t)，在信道中传播时分别伴有加性高斯噪声n2(t)和n2(t)满足以下模型：

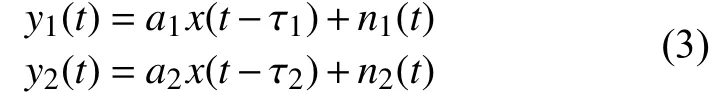
其中a1和a2分别表示输入信号经过不同信道传输后产生的幅值和相位的变化， τ1与 τ2为信号传输时延。将上式进行归一化得：

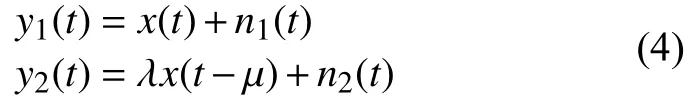
其中 λ =a1/a2表示接收信号的幅值比，μ为两信号的时延差。如图6所示为互相关算法工作原理图。

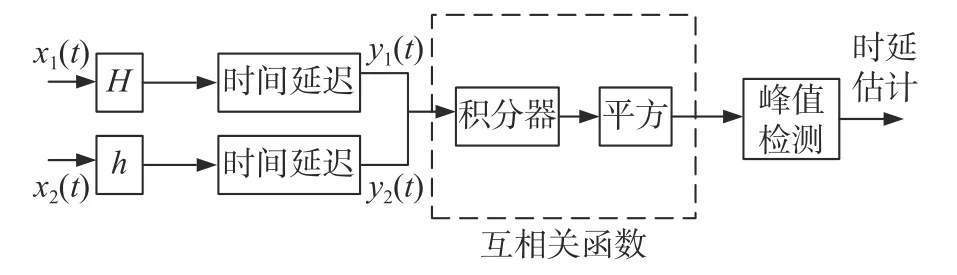
图6 互相关算法工作原理

其中，H为信道1的传递函数，h为信道2的传递函数。两输入信号的互相关函数为：

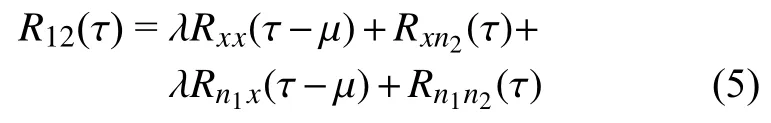
由于假设噪声独立于输入信号，则两输入信号的互相关函数简化为：

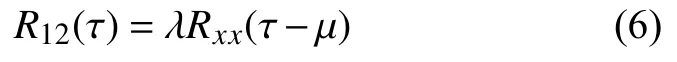
其中 τ在正负无穷之间。当τ=μ时，根据自相关函数性质 |Rxx(t)|≤Rxx(0)，自相关函数达到最大。此时τ为超声波在区截与端面处的回波时延值。

3.2 结果及分析

将传感器全量程分成若干等间隔点，输入标准量值并记录对应的输出值，对传感器进行正、反行程反复多次测试，并对测试数据进行处理。

测试过程中，检定炉每升温100 ℃，保持5～10 min达到热平衡后采集一次数据。如图7、8所示分别为在600 ℃和1 800 ℃采集到的超声回波信号。

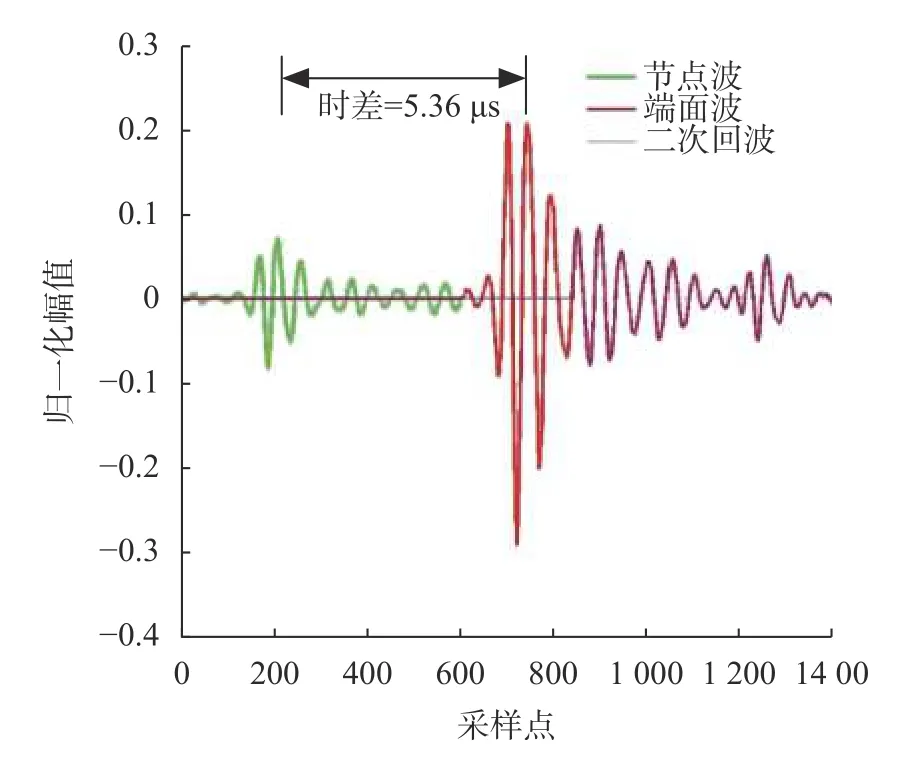
图7 600 ℃信号采集与处理

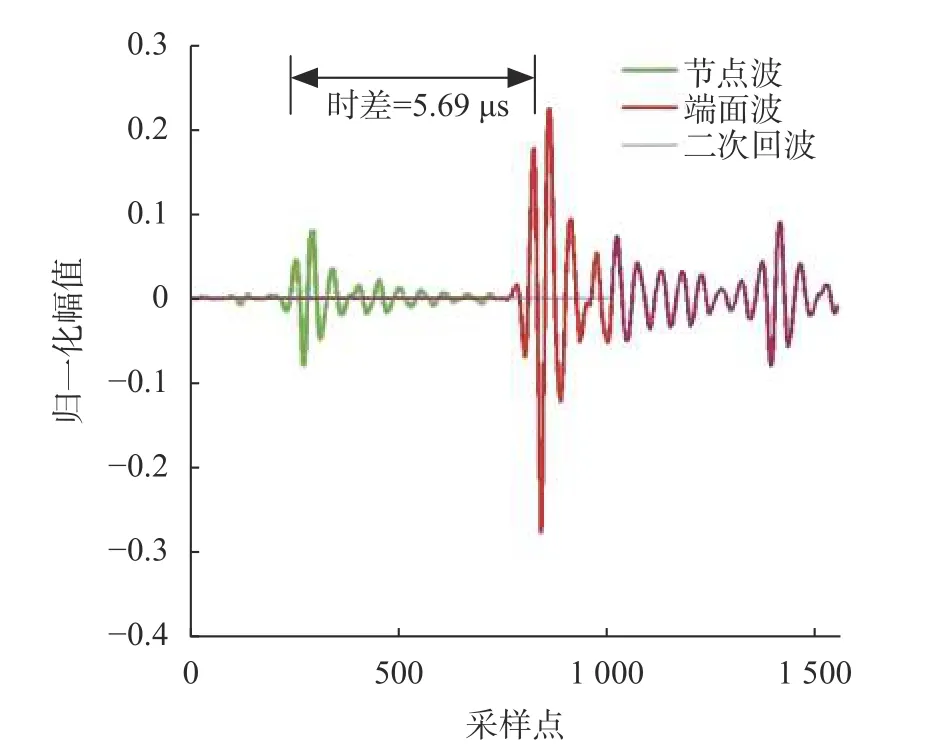
图8 1 800 ℃信号采集和处理

重复多次试验后，以600 ℃和1 800 ℃信号采集与处理过程为例，从图7和图8可以较为清晰地分辨出端面波、节点波及二次回波信号。利用互相关算法选取端面波与一次回波并计算传输时差，计算得1 800 ℃时传输时差为5.69 μs，声速为9 841.828 m/s。温度-时延拟合方程式为

计算了600～1 800 ℃范围内13个温度点的传输时延，且自由度均为12。如图9所示为不同温度点处的回波信号。

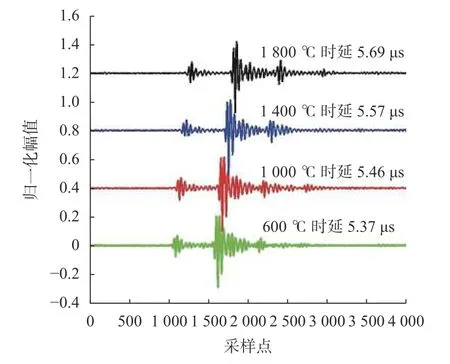
图9 不同温度点回波信号对比

由图可知，随着炉内温度的升高，超声波在波导杆中传播速度减小。如图10所示为温度与声速拟合曲线图，如表1所示为部分测试结果数据。平均拟合出温度与声速之间的函数式为

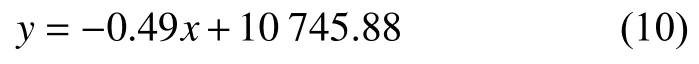
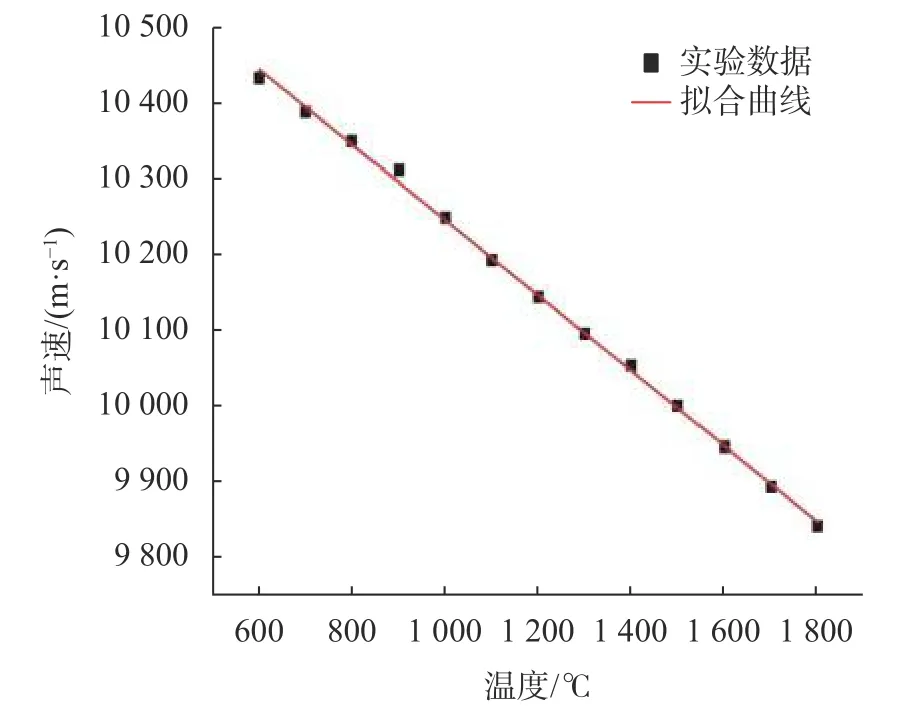
图10 温度-声速拟合曲线

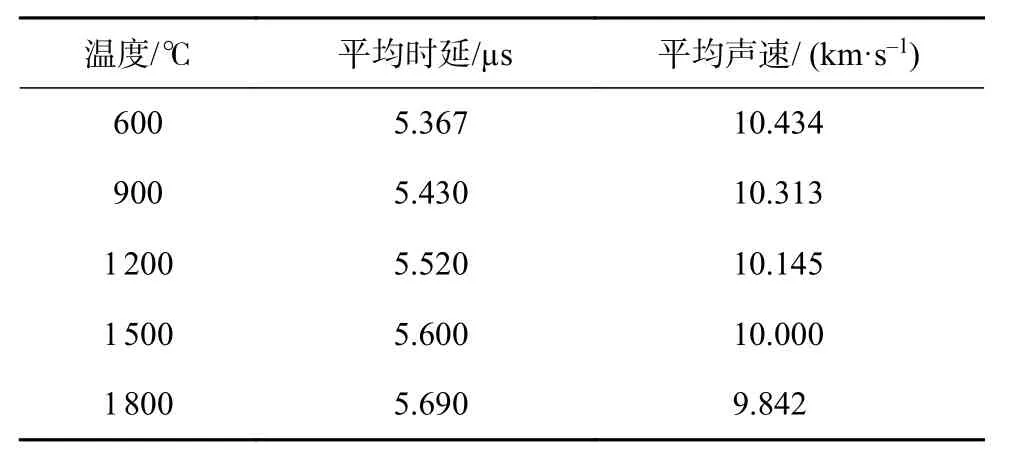
表1 温度-时延-声速数据表（部分）

根据传感器主要静态性能指标计算方法[19]和测量不确定度评定与表示标准[20]，对该超声温度传感器相关参数进行如下计算。

3.2.1 满量程输出

满量程输出(校准满量程输出)计算公式如下：

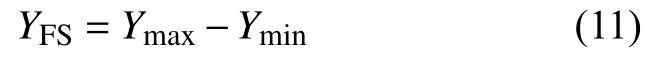
式中：Ymax——工作特性所决定的最大输出值；

Ymin——工作特性所决定的最小输出值。

回波信号的时延值在600～1 800 ℃范围内随温度升高逐渐增大。取最大输出值为1 800 ℃，最小输出值为600 ℃，则该温度传感器的满量程输出为 1 200 ℃。

3.2.2 灵敏度

传感器在第i个测量点处的灵敏度可用下式计算：

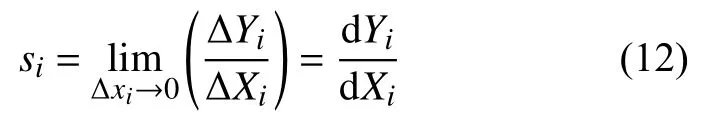
式中：ΔX——在第i个测量点上传感器的输入变化量；

ΔY——在第i个测量点上由ΔX引起的传感器的输出变化量。

线性传感器与非线性传感器的平均灵敏度计算公式如下：

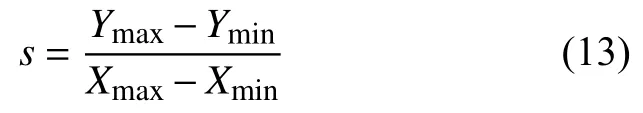
以900 ℃为分界点，低温段600～900 ℃平均灵敏度达0.110 m/s，高温段900～1 800 ℃平均灵敏度达0.072 m/s。结果表明高温段平均灵敏度更大，该超声温度传感器更适用于高温测试。

3.2.3 滞后性

滞后性用于描述传感器的正反行程实际平均特性之间的不一致程度，其计算公式如下：

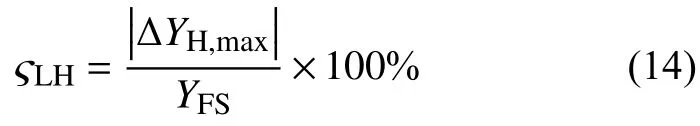
其中 ΔYH,max满足以下关系：

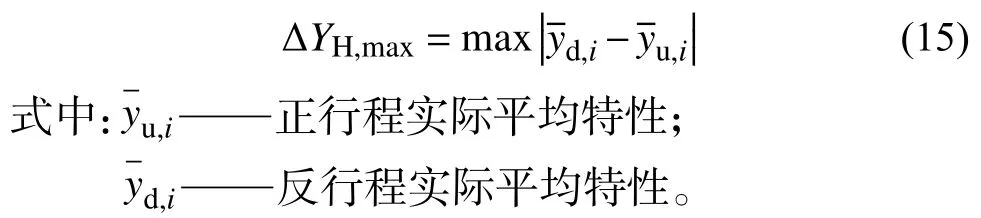
由ΔYH,max=4.08℃计算得到该温度传感器的滞后性为0.34%。表明传感器对于温场变化较敏感，能够实现静态温度点实时测量。

3.2.4 重复性

传感器的重复性是其偶然误差的极限值。传感器在某校准点处的重复性可计算为在该校准点处的一组测量值的样本标准偏差在一定置信度下的极限值，并以其满量程输出的百分比来表示。重复性误差计算公式如下：

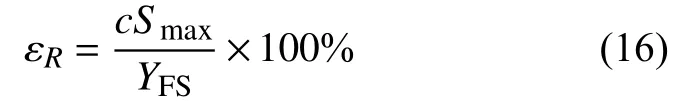
式中：c——包含因子，c=t0.95；

Sma—x最大的样本标准偏差；

YFS满量程输出。

对于小样本校准试验，一般按照t分布取包含因子，由于实验校准循环次数为3，则对应的95置信度包含因子为4.303。利用贝塞尔公式法计算得到1 300 ℃时最大的样本标准偏差为14.502 m/s。由上述数据计算得到1 300 ℃时该传感器重复性误差达到5.2%，即该温度点下重复性达到94.8%。表明传感器在1 300 ℃下测量误差最小，传感器各次试验的输出特性曲线的重合度较高。

3.2.5 不确定度

输入温度值所得时延值由标准不确定度的A类评定可知，假设n次独立重复观测值的估计输入量为xi,k，以1 300 ℃为例，A类不确定度贝塞尔公式计算如下：

计算得到A类不确定度为10.515 m/s。

根据超声收发仪的校准证书可知测量不确定度为1 % ，则高频脉冲测量值的最大偏差在 ± 1%，根据实际测量值拟合得到声速与温度的变化曲线,求导得到对应曲线斜率为0.49。按照均匀分布，可得到超声收发仪引入的B类不确定度为

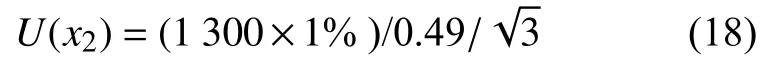
计算得到U(x2)=15.318 m/s。

在区截测量时，估计其长度以0.5概率落在27.8 ～28.4 mm之间。假设l服从均匀分布，其引入的B类标准不确定度为

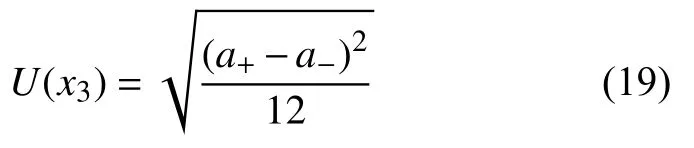
计算可得U(x3)=19.558 m/s。

根据上述计算合成标准不确定度

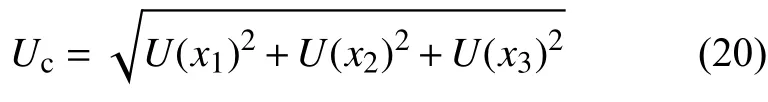
该传感器扩展不确定度为

获得合成标准不确定度为26.976 m/s，扩展不确定度为53.952 m/s。

综上所述，所搭建系统实现了对自制蓝宝石温度滞后性和重复性等特性的测试，能够解决未来超声温度传感器测试难题。

4 结束语

研究基于传统温度传感器测试方法，设计了一种超声温度传感器测试系统。选用蓝宝石材料制备超声温度传感器，研究了超声波在蓝宝石中的传播特性，利用该系统完成了蓝宝石温度传感器的测试。由传感器测试结果可知，该系统在600～1 800 ℃温度范围内工作特性良好，温度测试上限可达1 800 ℃。研究设计的超声温度传感器测试系统可以有效解决蓝宝石、尖晶石等超声温度传感器的高温测试问题。推动超声温度传感器更广泛地应用于航空、航天和军事等领域。