混沌系统在图像加密中的应用

◆宋玲玲 朱玉业

混沌系统在图像加密中的应用

◆宋玲玲 朱玉业

（滨州职业学院信息工程学院 山东 256603）

人工智能和网络技术的快速发展推动了大型任务的并行处理能力和智能化，使暴力破解所需的时间大大缩短，也使得基于特征分析的破解更加智能化，给数字图像加密技术提出了新的挑战。在分析和研究当前图像加密技术和方法的基础上，本文详细介绍了混沌系统及加密方法，详述了使用混沌系统进行图像加密过程，给出了图像加密算法的安全性分析和标准依据，同时提出了将混沌理论与其他相关技术相结合作为今后采用混沌系统进行图像加密的发展方向。

混沌系统；图像加密技术；安全性分析

“5G+云计算+人工智能”技术的融合推动了数字化经济的蓬勃发展，使数字图像作为一种常见信息载体的应用领域不断扩大，同时也推动了软件安全攻击技术的发展进步，对图像加密技术带来了新的挑战。由此，数字图像存储、传送和分发的安全性已成为各领域保证信息安全的关注焦点，图像加密技术成为图像处理技术研究的重中之重。近年来，许多专家和学者选择混沌系统为图像加密技术，取得了许多令人瞩目的成果，已经成为图像加密技术的一个重要分支。

1 图像加密技术分类

1.1 基于传统密码体制的图像加密技术

加密算法和密钥管理是加密系统的两个基本要素。传统密码体制中的加密算法是公开的，主要任务是对密钥进行管理。传统加密算法按照密钥类型可以分为单钥加密和双钥加密。单钥加密算法的加密和解密使用相同的密钥，常用算法有DES和AES。双钥加密算法的加解密使用不同的密钥，常用算法有RSA。理论上这些传统加密算法完全可以应用到图像加密技术中，但对于数据量大、冗余度高、相关性高的数字图像来说，直接应用这些算法加密效率较低。为提高加密效率，通常将传统加密算法与其他加密算法结合使用。实践证明，传统密码体制下的加密算法更适合文本信息的加密。

1.2 基于像素置换的图像加密技术

由于数字图像具有存储空间大、数据的空间域分布、相邻像素之间较强相关性等特有属性，可以通过改变像素位置、值转换等方法实现图像信息隐藏，对图像快速加密。图像置乱就是打乱明文图像像素之间的相邻关系，在空间上进行像素位置的重新排列组合，目的是在图像置乱后，使原始明文图像在视觉上变成无意义的混乱图像。常见的置换加密算法有猫脸变换、Puzzle变换、希尔伯特曲线变换等，因为这种矩阵变换不是完备的密钥系统，密码无法从算法中分离出来，因此在实际应用中受到很大限制。

1.3 基于混沌系统的图像加密技术

基于混沌系统的图像加密技术被越来越多的专家学者研究并广泛应用。混沌系统之所以能应用于图像加密技术，有以下两点原因：一是它本身具有与密码学相适应的特性，如：初值敏感性、不可预测性和内随机性等[1]；二是易于软件和硬件的实现。目前，混沌图像加密算法的研究主要分为两类，一类是基于混沌系统本身的算法研究及其改进优化，如：基于多维度混沌映射、超混沌系统和混沌压缩感知等技术的算法研究；另一类是与其他学科理论知识相结合用于提高算法安全和性能的加密算法，如：基于深度学习、DNA动态编码和机器学习神经网络等技术的算法研究。

2 混沌系统理论

2.1 混沌定义

以《Period Three Implies Chaos》的发表为标志，“混沌”正式成为表示一个确定系统具有无序或随机特性的学术术语。几十年来，从生物、工程、管理、人文到社会等领域产生了大量的混沌研究，虽然许多学者和研究者都试图给出“混沌”一个完整准确的定义，但是，仍然没有一个统一且涵盖“混沌”全部特性的定义产生，同时，这些定义都是一种定性的描述，而不是定量进行界定。以下为Li-Yorke给混沌作出的定义性描述。

（1）内无周期点；

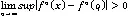
则称在上是混沌的。

2.2 典型的混沌系统

（1）Logistic映射

Logistic映射是一种非线性的离散迭代映射，最初被称为虫口模型。Logistic映射可以应用于不同的学科，比如描述有限空间内种群增长规律、生物种群的变化特征等。因其具有初值敏感性和内随机性等特性，目前被广泛应用于图像加密技术中。

Logistic映射是最基本的混沌函数，它本质是一种迭代函数，其算法公式为：

其中，x是系统状态，且0<<1；为系统参数，实验证明，取值在区间（3.5699，4）时，随着的增长，映射周期点的周期逐渐增大，图像上周期点出现分岔，出现为随机性，系统逐渐进入混沌状态，这时可以产生用于图像加密的随机序列。

（2）Henon映射

Henon映射是一种常用的二维可逆非线性混沌映射，由x和y两个变量同时控制，相对于一维混沌系统其结构更加复杂，也具有更好的混沌性能。其算法公式为：

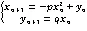
其中，、为系统控制参数，当=1.4，=0.3时，该系统出现混沌吸引子，系统处于混沌状态。

二维映射因为控制参数多了，算法较一维复杂，密钥长度增大，可以有效提高加密的安全性。

（3）Chen混沌系统

1999年，陈教授等人发现了一个新的混沌吸引子系统，该系统被其他研究者称为Chen混沌系统[2]。这个系统的描述为：

其中，、、为实参数，当=35，=3，=28时，系统处于混沌状态。

Chen系统属于三维映射，算法更加复杂，产生的动态轨迹更加杂乱、随机性强，加密安全性更高。

2.3 混沌系统的基本特征

（1）对初始值与系统参数的极度敏感性

混沌系统是一种具有“蝴蝶效应”的动力学系统，也就是说其初始值与系统参数即使有非常细微的变化也会引起相差很大的结果。加密时能够保证在知道一段混沌运动轨迹时也无法反推出其初始值，满足加密的安全性要求。

（2）有界性

虽然混沌系统的运动是无规则的，但并不是漫无边界的，它的运动轨迹都会在一个被称为混沌吸引域的区域空间内进行。不管初始值如何选择和变化，其运动轨迹都是有界的。

（3）长期不可预测性

由于混沌系统运动的不稳定性，且在混沌运动过程中会丢失之前的运动信息，所以造成根据前面的信息不能预测后面的运动状态。

（4）内随机性

系统的随机性是指该系统在不受外界干扰的情况下，某些状态的出现是不能根据之前状态做出准确预测的特性。对于大多数确定性系统来说，如果没有外界条件干扰，它的动态轨迹是确定和可预测的。然而，混沌系统作为一种确定性的动力系统，其运动轨迹在不受任何外界条件干扰的情况下会呈现出某些随机性，这种来自系统自身的完全无序或完全无规则的运动称为内在随机性[3]。

3 基于混沌系统的图像加密实现方法

混沌图像加密技术的实质是使用混沌系统生成随机序列，由随机序列和明文图像数据进行某种运算得到密文图像数据，加密后的密文图像是杂乱无章的，从而实现加密的目的。根据图像数据的特点，现行的数字图像加密技术实现方法一般有三种：一是像素位置置乱，二是像素灰度值扩散，三是这两者的结合。

3.1 像素位置置乱

像素位置置乱是将像素相对位置打乱，减少视觉上可辨识信息的过程，有许多种实现方法，基于混沌映射的置乱就是其中一个非常重要的方法。混沌置乱是一种具有加密性质的方法，可以完整将置乱数据恢复为原始图像。使用混沌置乱，首先将混沌运动轨迹转换成与图像像素位置相关的序列或矩阵。采用一维混沌系统时，可以将轨迹进行排序，利用轨迹点的序号与像素位置进行映射。采用多维混沌系统时，可任选一维数据或进行某种函数运算生成一维数据，然后进行排序，与像素位置进行映射，由此完成像素位置置乱。

原始图像像素经过位置置乱后，整幅图像会变为类似噪声的花点图像，像素之间的关联被打破，这样破解者也就无法得到原始图像的真实信息。像素位置置乱虽然能够对图像进行加密，但这种加密只是改变了像素点的位置信息，没有改变像素值的统计特性，破解者仍可以通过统计分析图像特征破解加密图像。

3.2 像素值扩散

像素值扩散是将数据图像的每一个像素值都转变为其他的像素值，这样从根本上改变了图像像素值的统计特性，较好地隐藏了明文图像的数据信息，攻击者不容易通过统计特征破解加密图像，弥补了像素位置置乱方法的不足。扩散加密通常使用异或运算对图像像素值进行改变，具体方法是使用混沌系统产生的随机序列和明文图像数据进行异或运算，改变像素值的大小，从而达到加密图像的目的。

3.3 混合加密

位置置乱加密方法仅仅改变了像素的位置，没有改变像素值的大小；扩散加密方法仅对像素值进行了变换，没有对像素位置进行变换。因此这两种加密方法的安全性都不高。为提高加密的安全等级，已将置乱和扩散相融合的加密方法作为典型的图像加密方法。实验证明，这种混合加密方法的安全性比单纯的置乱和扩散方法安全性要高。

4 图像加密的安全性分析

4.1 密钥空间分析

现代加密科学体系下，只要给定足够的时间，就能够破解密码，算法不被破解是在特定的时间周期内不被破解。算法抵御穷举攻击最根本的保证是由密码的数量决定的。密码数量是由算法密钥空间，即密钥的长度和广度决定的。密钥的广度决定了密钥可选择使用字符或编码的范围；密钥的长度决定了一个密码所包含字符或编码的总长度。密钥越长、广度越大，则可选密钥数量就越大，枚举需要的时间就越长，被暴力破解的平均用时就越长。一般情况下，一个好的加密算法的密码数量应该大于2100，才能抵御穷举攻击[4]。随着云计算和其他并行计算的出现，对于一个成熟算法暴力破解的平均用时变得越来越短，目前一些重要的加密场合下，密钥长度已经要求大于等于2048位，密钥数量已经达到22048。所以，密钥空间分析对于算法来说特别重要，可以协助算法来设计和选择恰当的密钥长度，确定密钥的广度，保证算法的强壮性。

4.2 密文直方图分析

如果图像加密仅使用像素值置乱的方法进行加密，不会改变图像中像素值的分布频率，攻击者便可以使用直方图对密文图像进行分析，找到明文和密文相近的统计特征，找出加密算法，破解一系列密文图像。为了抵御这种统计分析的密码破解方式，必须将明文的统计信息隐藏，具体做法就是通过算法改变图像像素值，对像素值进行扩散。图像进行像素扩散后，密文图像的像素直方图变化平缓，使得与明文图像像素直方图分布特征完全不相关，能够有效抵御统计分析攻击。

4.3 相邻像素相关性分析

一般情况下，明文图像的相邻像素值都有一定的相关性。通常图像加密算法都会对像素位置进行置乱，置乱后的相邻像素一般不具有相关性。加密后相邻像素值的相关性越差，说明算法越好，能够较好抵御像素相关性分析攻击[5]。

4.4 信息熵分析

信息熵是衡量和表征图像信息量大小的物理量，一幅图像经过变换后，信息是否有损失可以用信息熵的变化来表达。如果图像变换后信息熵变化不大或者没有变化，则变换后图像就可以很好地还原成原始图像，如信息熵变化很大，则就不能恢复成原始图像。图像加密实际上是一种复杂的图像变换，因此，若加密后图像信息熵损失过大，则解密后图像就很难解密成原始图像，所以图像加密算法必须保证加密前后图像信息熵相等或仅有微小差异。因此，保持信息熵稳定是衡量图像加密算法质量的一个重要指标。

5 结束语

本文针对数字图像加密技术，分析了目前主要图像加密算法，重点对基于混沌系统的加密技术进行了研究和分析。混沌系统因其自身具有的初值敏感性、不可预测性和内随机性等特性，被广泛应用于现代图像加密领域。文中对混沌系统的定义和特性、基于混沌系统的加密实现方法以及图像加密的安全性分析进行了介绍和研究。基于混沌系统的图像加密技术是目前图像加密技术的一个重要领域，要想使混沌加密理论得到长足发展，不仅要对混沌算法进行改进和优化，还需要将混沌理论与其他相关技术相结合。

[1]薄䘵裕.基于混沌和分形的两类图像处理算法[D].南京邮电大学，2012.

[2]汪小帆.Chen’s吸引子—一个新的混沌吸引子[J].控制理论与应用，1999.

[3]陈士华，陆君安.混沌动力学初步[M].武汉：武汉大学出版社，1998.

[4]何波.混沌加密算法与Hash函数构造研究[M].电子工业出版社，2011.

[5]杨璐，邵利平等.基于迷宫置换和Logistic混沌映射的图像加密算法[J].计算机应用，2014.