一种用于空间结构的新型聚酰亚胺薄膜的力学特性

刘朋博，张华振，徐 婷，唐渝思，徐 斌

(1.中国空间技术研究院西安分院，西安 710000；2.航天跃盛(杭州)信息技术有限公司上海分公司，上海 201107)

0 引言

以薄膜结构为主体的天线[1-3]、太阳帆[4-5]、太阳能电池阵列[6]等正在受到研究人员越来越多的关注。聚酰亚胺(polyimide,PI)薄膜因其具有面密度低，轻质和柔韧等特点，成为以上空间结构中首选的薄膜材料。1960年美国杜邦公司开发出PI高分子薄膜(Kapton 系列)，该材料在-200 ℃～260 ℃范围以其优异的力学性能、电气绝缘性能、化学稳定性和抗辐射性能等受到广泛的关注。对于在空间结构中使用的薄膜而言，力学性能尤为重要。以大型的张拉薄膜天线为例，模量与泊松比会对其性能产生较大的影响。随着新型需求的不断提出，具有优异力学性能的PI薄膜将成为空间结构领域新的研究热点。

当前对于PI薄膜的性能优化，主要集中在利用纳米级粒子对薄膜进行填充上，诸如纳米级的石墨烯[7]、氧化石墨烯[8-15]、SiO2[16-17]、SiC[18-19]、六方氮化硼纳米片[20](boron nitride nanosheets，BNNSs)和粘土(montmorillonite，MT)[21-23]。近年来的研究显示，纳米纤维填充得到的复合薄膜性能高于由无机粒子填充的薄膜。赵依纯等[24]的研究表明，当复合薄膜中纳米PI纤维质量百分含量为10%时，其热膨胀系数值比纯薄膜降低了40.3%。拉伸模量和拉伸强度分别提高了89.5%和132.9%。此外，微波辐射也被用于PI薄膜的性能优化中，CHOI等[25]的研究表明，微波辐射可以在提高(或保持)PI薄膜柔韧性的同时提高拉伸强度，改善PI薄膜的力学性能。通过对PAA溶液进行微波辐射并随后进行热酰亚胺化来制备PI膜，经微波处理的PI薄膜的拉伸强度比作为对照的薄膜高27%，断裂伸长率最高增加了32%。然而，当前对薄膜改性增强的研究中，少有探讨改性方案对薄膜泊松比影响的案例。

针对应用于空间结构中的PI薄膜，采用高强度高模量的PI纤维对其进行同质增强，制备得到正交各向异性的高性能PI复合膜。由于同质纤维与基体树脂结构相似，界面的相容性好，制备得到的PI复合膜具有较好的拉伸性能。主要考察不同经向纤维分布密度对复合膜经纬两个方向的拉伸强度、断裂伸长率、杨氏模量和泊松比的影响。同时，借助理论计算和有限元仿真分析复合纤维膜的杨氏模量和泊松比，并与实验测定结果进行对比分析。

1 PI复合膜的制备和性能分析

1.1 试剂、制备过程、测试和表征

质量分数为20%的聚酰胺酸(PAA)溶液，溶剂为N,N-二甲基乙酰胺(DMAc)。聚酰亚胺纤维的单丝直径为11 μm，断裂强度3.70 GPa，初始模量121 GPa，断裂伸长率3.24%，50根丝构成一束。

实验制备了6种不同经向纤维密度n的薄膜，分别为0束/cm，1束/cm，5束/cm，10束/cm，15束/cm，20束/cm。如果仅在一个方向放置PI纤维，那么制备得到的复合膜将非常容易沿着纤维间隙撕裂。为此，通过在纬向增加1束/cm的PI纤维来抑制薄膜可能发生的撕裂。PI复合膜示意图如图1所示。

图1 PI复合膜的示意图Fig.1 Diagram of fiber reinforced PI film

除了上述6种复合膜外，还制备了纯薄膜作为对照。纯薄膜与0束/cm的复合膜区别在于0束/cm的复合膜仍然有纬向纤维。研究中，纯薄膜作为力学性能的比较基准，0束/cm的复合膜作为增强的出发点，排除纬向纤维对纤维增强中力学性能带来的影响。表1列出PI复合膜的经向纤维密度及其对应的纤维体积分数。

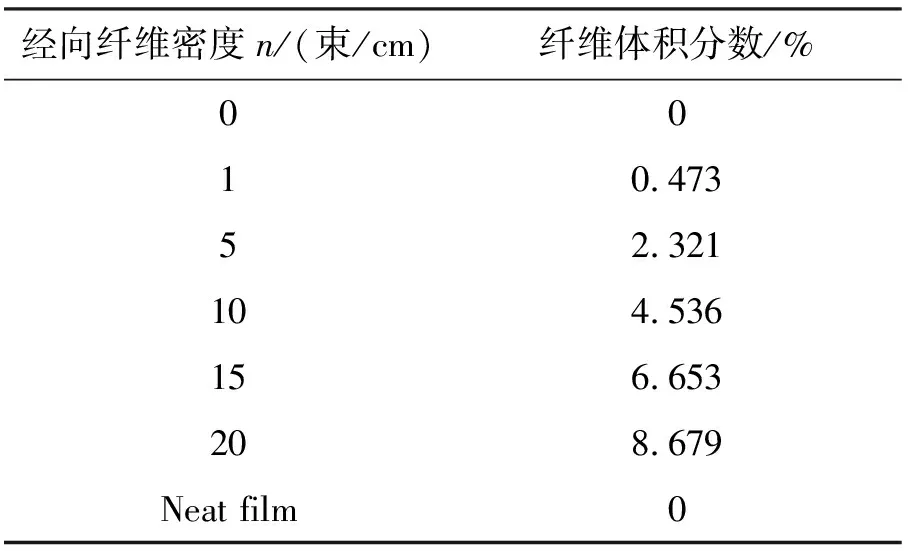
表1 PI复合膜经向纤维密度及体积分数

为观察PI复合膜截面中纤维束的分布位置，先对复合膜截面进行喷金处理，后采用金相镶嵌料对薄膜样品进行镶嵌。最后采用NOVA Nano SEM 230 场发射扫描电子显微镜对样品进行观察。

PI复合膜的拉伸强度、断裂伸长率、杨氏模量和泊松比采用INSTRON 68TM-30拉伸机配合双向测试的2663-901 AVE2非接触式双向引伸计进行测定，夹具为2712-045 5 KN气动夹具，试样大小为100 mm×20 mm，拉伸方向标距为50 mm，横向标距为10 mm，加载速率是10 mm/min，每种复合膜样品测试3个。

1.2 PI复合膜中纤维的分布

经向纤维密度为10束/cm的PI复合膜的经向截面SEM样品及其SEM图如图2所示。可以看出，PI复合膜一面平滑，另一面在纤维分布的位置有一处弧形的凸出。纤维束沿PI复合膜厚度方向分布的位置偏向于复合膜光滑面一侧。同一纤维束在薄膜中聚成一团，与薄膜基体结合紧密，从而使得PI复合膜沿经向纤维方向表现出较好的拉伸性能。

图2 PI复合膜的经向截面样品和SEM照片Fig.2 Sample and SEM image of PI composite film’s warp cross-section

1.3 PI复合膜的拉伸强度和断裂伸长率

图3(a)为PI复合膜在经向拉伸中的应力-应变曲线。从应力-应变曲线可以看出，随着复合膜的经向纤维密度n(纤维束/cm)增大，PI复合膜的拉伸强度和杨氏模量变大，而断裂伸长率则减小。除此之外，PI复合膜的材料特性逐渐由塑性演化为脆性。当n=20时，PI复合膜的应力-应变曲线几乎为一条直线。

图3(b)为PI复合膜的纬向拉伸曲线。可以看出经向纤维密度的变化对复合膜的纬向拉伸影响主要体现在断裂伸长率和拉伸强度的变化上，不同经向纤维密度的复合膜纬向杨氏模量之间的差距并不大，且均为塑性。

不同经向纤维密度n的PI复合膜的经向拉伸强度S1和纬向拉伸强度S2随经向纤维密度n的变化如图3(c) 所示。

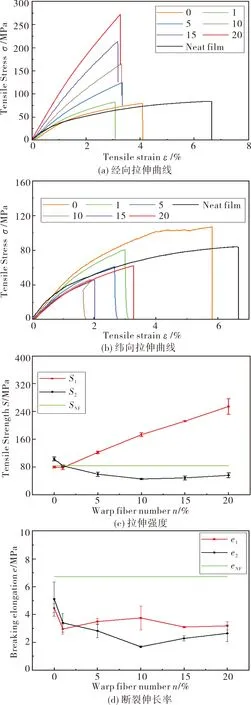
图3 PI复合膜的应力-应变曲线、拉伸强度和断裂伸长率Fig.3 Stress-strain curves, tensile strengths, and breaking elongations of the PI composite films

PI复合膜的经向拉伸强度S1随着经向纤维密度n的增大而增大。当n=0时，PI复合膜的经向拉伸强度S1(80.18 MPa)与纯薄膜的拉伸强度SNF(84.09 MPa)相差4.88%，这是由于复合膜有1束/cm纬向纤维存在所导致的。当n=10时，S1(173.25 MPa)较之纯薄膜的拉伸强度SNF提高了106%。当n=20时，S1(254.52 MPa)较之SNF提高了203%。

PI复合膜的纬向拉伸强度S2的测试值随着经向纤维密度n的增大呈现出先减小，后略有增大的趋势。当n=0时，S2(103.75 MPa)与纯薄膜的拉伸强度SNF(84.09 MPa)相差18.94%。当n=10时，S2(45.76 MPa)仅为SNF的54%。在n=15和n=20时，PI复合膜的纬向拉伸强度S2分别为48.78 MPa和56.26 MPa，分别为SNF的58.01%和67%。这说明经向纤维密度n对S2的影响在n≥10时基本趋于平稳。

PI复合膜的断裂伸长率e如图3(d)所示。经向断裂伸长率e1随n的增加呈现先减小，再逐渐增大，最后逐渐减小的趋势。纬向e2则时先减小，然后增大的趋势。当n=20时，二者都落在3%左右，与纤维的断裂伸长率3.24%基本一致。纯薄膜的断裂伸长率eNF为6.73%，远大于PI复合膜经纬双向的断裂伸长率e1和e2。这说明当引入了纤维之后，PI复合膜的断裂伸长率的大小受纤维体积分数的影响较小。

1.4 PI复合膜的杨氏模量

根据复合材料混合定律(rule of mixture,ROM)可以通过计算得到PI复合膜的性能参数，ROM模型如式(1)所示：

φc=φfVf+φm(1-Vf)

(1)

式(1)中，φc为PI复合膜平行于纤维方向的性能参数；φf为纤维的性能参数；φm为薄膜基质的聚酰亚胺树脂沿纤维方向的性能参数；Vf为PI复合膜中纤维的体积分数。

对于本研究中的PI复合膜而言，需要讨论其经纬双向的力学性能，而ROM模型只能计算复合膜沿纤维方向的力学参数。所以对于PI复合膜而言，ROM模型在讨论经向力学性能时仅考虑经向纤维，在讨论纬向力学性能时只考虑为抑制薄膜撕裂加入的纬向纤维带来的增强效果。

通过有限元分析(finite element analysis,FEA)可以得到PI复合膜的杨氏模量E和泊松比μ，为了简化模型，有限元分析只考虑经向纤维。如图4所示，约束矩形PI复合膜的两个互相垂直的边界，所有在这两个边界上的节点只能在沿其边界方向上平动。对PI复合膜的其中一个自由边界施加垂直于该边界的位移载荷，即可计算得到PI复合膜沿位移方向的等效杨氏模量Eeff。以复合膜其中一个方向为例，Eeff的计算方法如式(2)所示[26]：

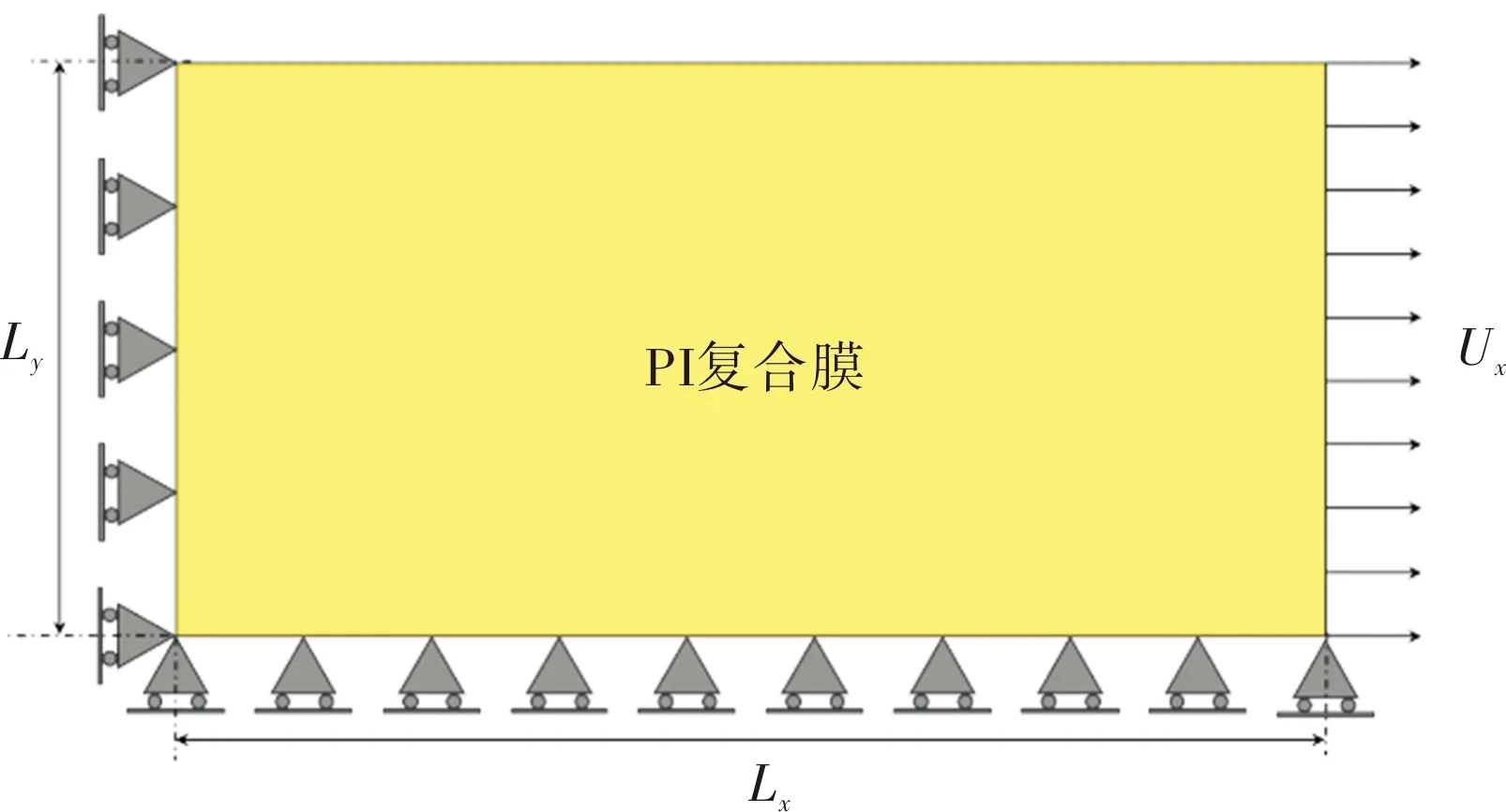
图4 FEA模型的约束和载荷Fig.4 Constraints and loads of the FEA model

(2)

式(2)中，Ex,eff为PI复合膜x方向的等效杨氏模量；W为整个PI复合膜的应变能；t为薄膜的等效厚度；Ux为沿x方向施加的位移载荷；Lx和Ly分别为沿x方向和y方向的复合膜的边长。

通过ROM(经向)计算、FEA仿真和实验测得的PI复合膜的经向杨氏模量E1如图5(a)所示，同时增加纯薄膜的杨氏模量ENF-TEST作为对照。可以看出，PI复合膜的经向模量E1-TEST随经向纤维密度n的增大而不断增大。当n=0时，E1-TEST为3.19 GPa，为纯薄膜的杨氏模量ENF-TEST(3.245 GPa)的98%，同样是由于纬向纤维的存在所导致。而当n=20时，E1-TEST为9.74 GPa，较之ENF-TEST提高了202%。与实际测得的模量E1-TEST相比，使用ROM模型和FEA模型两种方法分别计算得出的经向模量E1-ROM和E1-FEA在n=0时，均为3.245 GPa，与纯薄膜的杨氏模量ENF-TEST一致，这是因为这两种模型在此时均退化成为纯薄膜。此后随着经向纤维密度n的增大，E1-ROM和E1-FEA相较于测试值E1-TEST偏大，这是由于ROM模型(经向)和FEA模型均未考虑纬向纤维的原因。

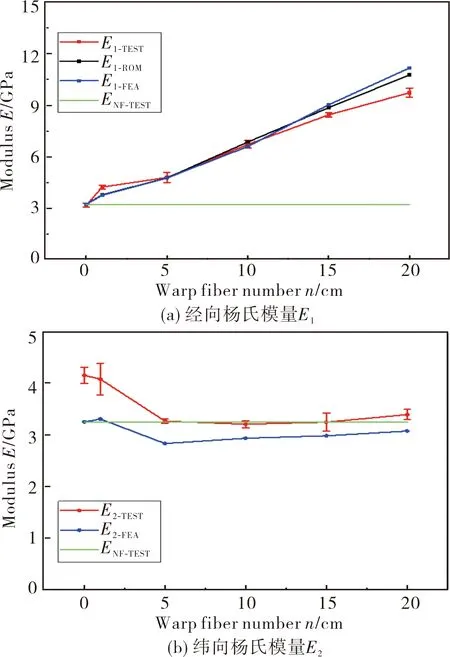
图5 PI复合膜的杨氏模量Fig.5 The Young’s modulus of PI composite films

通过ROM(纬向)计算、FEA仿真和实验得到的PI复合膜的纬向杨氏模量E2如图5(b)所示，同时增加纯薄膜的杨氏模量ENF-TEST作为对照。实验测得的纬向模量E2-TEST随着n的增加先减小，当n≥5时，逐渐趋于平稳。当n=0时，E2-TEST为4.15 GPa。当n=5时，E2-TEST减小为3.26 GPa，为n=0时的78.55%。这说明经向纤维的引入会造成纬向模量的减弱。当n分别等于10，15，20时，E2-TEST与n=5时相差1.84%、1.23%和3.99%，可认为此时E2-TEST已经趋于稳定。说明n=5以后的经向纤维密度n的增加对纬向模量几乎不再产生影响。E2-TEST随着n的变化趋势与FEA模型仿真所得的E2-FEA是一致的，且E2-FEA一直小于E2-TEST，原因在于FEA模型只考虑了经向纤维的影响，而为了防撕裂引入的纬向纤维有一定的增强作用。

1.5 PI复合膜的泊松比

PI复合膜的泊松比同样可以通过FEA模型仿真得到，对于图4所示的FEA模型，等效泊松比μeff如式(3)所示[26]：

(3)

式(3)中，μxy,eff为复合膜的泊松比；Uy为复合膜上边界y方向的位移，其余符号意义与式(2)相同。

当n分别等于10，15，20时，由于经向纤维过于密集，导致材料的纬向泊松比μ21难以测量，所以此时的纬向泊松比由正交各向异性材料经纬方向的模量和泊松比的关系如式(4)所示：

(4)

式(4)中，μ21为纬向泊松比；E2为纬向的杨氏模量；μ12为经向泊松比；E1为经向杨氏模量。

通过ROM计算、FEA仿真和实验测得的PI复合膜的经向泊松比μ12如图6(a)所示，同时加上纯薄膜的泊松比μNF-TEST作为对照。可以看到，PI复合膜经向泊松比μ12-TEST随着经向纤维密度n的增加在纯薄膜的泊松比μNF-TEST上下波动，但偏移不大。同样地，采用FEA模型仿真得到的经向泊松比也在μNF-TEST上下波动。而通过ROM计算得到的经向泊松比μ12-ROM与μNF-TEST的值几乎一致，随n的变化波动很小。

通过ROM计算、FEA仿真和实验测得的PI复合膜的纬向泊松比μ21如图6(b)所示，同时加上纯薄膜的泊松比μNF-TEST作为对照。n=0时，PI复合膜的纬向泊松比μ21-TEST略大于μNF-TEST。随着n的增加，实验测定FEA模型二者得到的纬向泊松比μ21-TEST和μ21-FEA都不断下降。FEA模型较准确地预测了μ21-TEST的值。

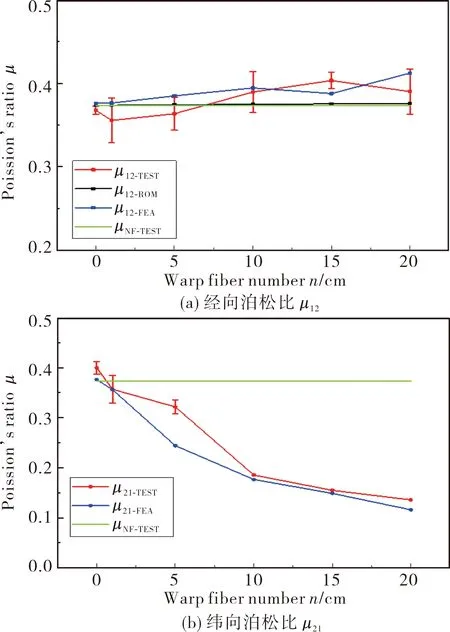
图6 PI复合膜的泊松比Fig.6 Poisson’s ratios of PI composite films

2 结论

1)通过使用同质的聚酰亚胺纤维对聚酰亚胺薄膜进行增强，可制备得到用于空间结构的高强度高模量的正交各向异性PI复合膜。

2)随着经向纤维密度的增加，在PI复合膜的经向拉伸强度得到提高的同时，纬向拉伸强度随经向纤维束的增多略有降低，后趋于一个稳定值。在引入纤维之后，薄膜的经纬双向断裂伸长率均远低于纯薄膜的断裂伸长率(6.73%)。随着经向纤维增多，断裂伸长率最终基本接近增强所用的PI纤维的断裂伸长率(3.24%)。

3)PI复合膜的经向杨氏模量随经向纤维密度的增加不断增加，与ROM模型和有限元模型的计算结果吻合。而其纬向杨氏模量先是略有下降，而后趋于稳定，有限元模型准确地预测了这一趋势。

4)PI复合膜的经向泊松比基本不随经向纤维的加入而变化，有限元模型分析结果和ROM计算结果均佐证了这一点。而随着经向纤维密度的增加，复合膜的纬向泊松比不断减小，趋势与有限元模型计算得到的预测一致，且符合正交各向异性材料的规律。