一种高稳定正弦载波产生电路的设计与研究
2022-03-20张文艳雷军刚李云鹏徐恒通
张文艳,雷军刚,李云鹏,徐恒通
(兰州空间技术物理研究所,兰州 730000)
0 引言
静电悬浮加速度计是一种电容式加速度传感器,主要应用于低频空间探测系统,通过检测质量块与电极之间构成的电容差来测量敏感加速度信号,惯性传感器的测量精度会受限于电容位移检测电路的实现水平。电容位移检测电路是实现精密测量的关键,而高稳定正弦载波技术是实现电容差精密传输的重要载体[1]。
高稳定正弦载波产生电路为质量块提供1个100 kHz的正弦载波检测电压,将缓慢的电容差信号调制成100 kHz的幅度调制信号,通过解调电路从幅度调制信号中分离出接近直流的电压信号。正弦载波的幅值稳定度会影响电容位移的传感噪声,电容位移传感器的信噪比会随注入正弦载波幅度稳定性的提高而提高;同时,正弦载波的幅度作为传感电路的增益注入质量块,该幅度的任何波动都会随着质量块的实际位移而倍增,导致噪声增大。
正弦载波的幅值稳定度会直接影响电容位移传感的精度,本文提出一种基于高幅值稳定度的正弦载波产生方案,该方案主要通过将直流信号进行分压并滤波输出正弦载波。由于直流信号的低频特性会通过振荡分频直接影响正弦载波的幅值稳定度,因此,本文对该方案在1 mHz~10 Hz低频频段内的电路噪声性能进行研究。

(1)

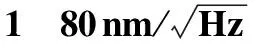
表传感偏移量时传感桥的参数
1 正弦载波产生方式
1.1 传统正弦载波产生方式的局限性
模拟产生方式LC振荡电路受品质因数Q影响,产生波形的频率稳定度只能达到10-3~10-5量级,温漂、时漂较大,石英晶体在其基础上利用元件固有特性提高了电路的品质因数Q,波形的频率稳定度可达到10-9~10-11量级,但晶体振荡器灵活性差,产生的正弦载波受器件电源电压的限制波形会有所失真,且上述两种方式在其应用中均未提及幅值稳定性,不符合本文应用要求[2];直接数字频率合成(direct digital system, DDS)基于取样和计算技术产生的正弦载波,具有频率分辨率高、相位噪声低、信号纯度高等优点[3]。
DDS是一种从参考频率源生成多种频率的数字控制方法,从相位概念出发直接合成所需波形。如图1所示,在参考时钟fc的控制下,频率控制字K由相位累加器累加得到相应的相码,波形存储器进行相码-幅码变换输出不同的幅度编码,经过DAC输出相应的阶梯波,低通滤波器对阶梯波进行平滑,最终得到由频率控制字K决定的可连续变化的输出波形[4]。
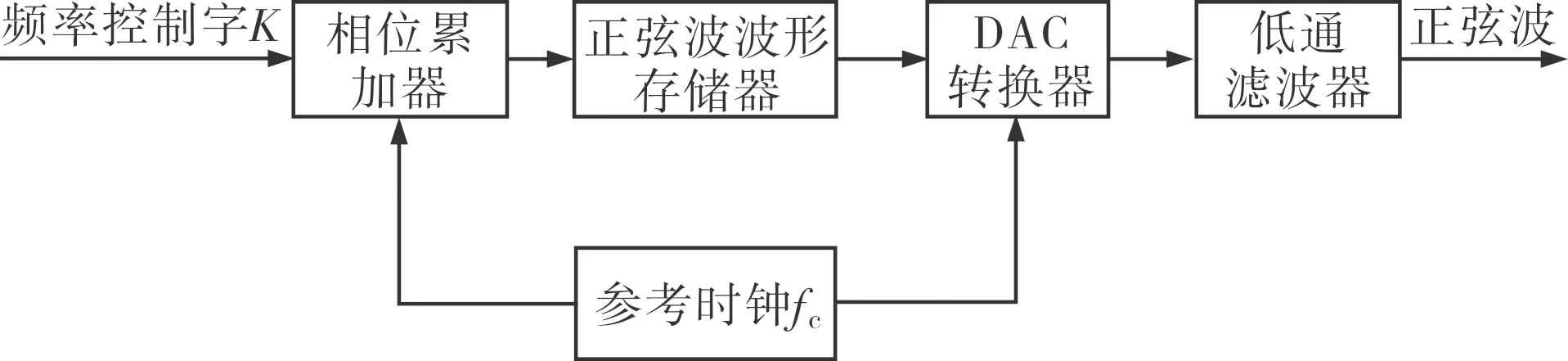
图1 DDS合成器的构成框图Fig.1 Block diagram of DDS synthesizer
对于正弦载波信号,信号频率由相位变化速率唯一确定,将2π弧度作N位量化,相位增量对应量化后的值定义为频率控制字K,输出信号频率f0为:
(2)
其中,K是频率控制字,N是量化位数,fc是参考时钟,f0是输出信号频率。
在时钟控制下,每个周期对相位控制字累加,对所得到的相位编码作正弦函数转换,得到对应的幅度输出,DDS的输出序列如式(3)所示:
(3)
其中,n是累加次数,S(n)是DDS的输出序列。
在DDS合成理论上,要想得到高幅值稳定度的100 kHz正弦载波,DDS各部分性能必须是理想的,即[4]:
1)相位累加器的位数趋于无穷大,所有输出均用于寻址波形存储器;
2)波形存储器的地址区域趋于无穷大,且每个单元波形采样数据位数趋于无穷大;
3)DAC输入数据位数D趋于无穷大,且具有理想的数模转换特性;
4)低通滤波器具有理想的低通特性;
5)参考时钟频率稳定,无相位抖动,且频率趋于无穷大。
在实际应用中,DDS产生正弦载波的工作原理是基于数字取样及数模转换技术,由于理想DDS的不可实现性,输出正弦载波的幅值稳定度受到其工作原理的限制,各器件的非理想特性均会给DDS输出的正弦载波带来杂散[4]。
1.2 高稳定正弦载波产生方案
针对惯性传感器中高精度电容位移传感所需的100 kHz高稳定正弦载波的应用需求,本方案在DDS基本原理的基础上,对影响输出波形幅值稳定度的因素进行改良,主要有以下方面:
1)DDS产生电路要求DAC输出阶梯波的每一阶梯都具有极高的幅值稳定度,在本文中采用DAC输出恒定的直流信号,这一改良措施降低对DAC器件的要求,提高DAC输出直流信号的幅值稳定度;
2)针对DDS中通过相位-幅度转换得到每一阶梯值,本方案采用精密低漂移电阻对恒定直流进行分压,这一改良措施降低DDS中因相位截断和幅值量化引入的误差;
3)对于DDS中参考时钟的引入,本方案将其只应用于多路复用器的选通,减小DDS中参考时钟引入的相位噪声。
如图2所示,本方案采用DAC将基准电压转换成直流电压信号,直流输出电压通过正反相缓冲器输出正、负直流量,经过高精度电阻进行分压;晶体振荡器和分频器组成振荡分频器,通过计数器产生所需的时钟信号,阶梯波合成电路将振荡分频电路输出的时钟信号循环移位,使得多路复用器的输出端输出不同电平组合得到的阶梯波,之后通过低通滤波器滤除合成正弦载波中的谐波成分,输出具有高幅值稳定度的正弦载波。
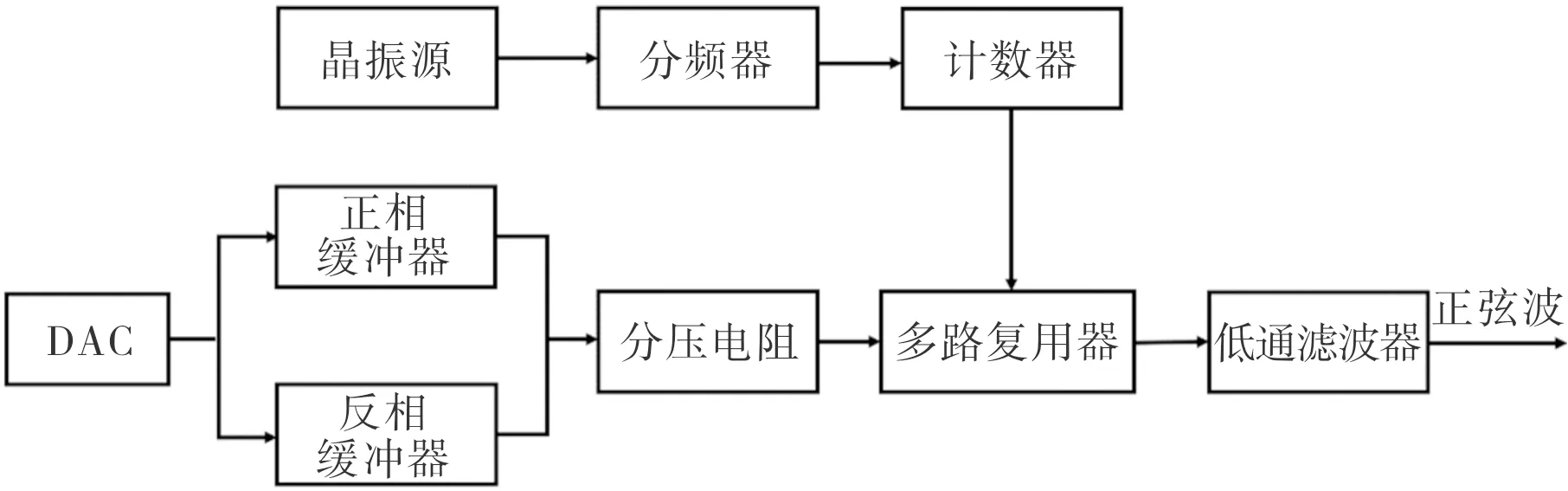
图2 基于DDS技术改良的阶梯波滤波电路Fig.2 Improved step wave filter circuit based on DDS technology
2 电路噪声分析
根据惯性传感器中高精度电容位移传感所需的100 kHz高稳定正弦载波的应用需求,本文需要对正弦载波产生电路在1 mHz~10 Hz频段范围内的电压参考噪声e(n)进行分析。
2.1 正弦载波产生电路的噪声分配
在研究频段1 mHz~10 Hz范围内,幅值为5 V的正弦载波产生电路的电压参考噪声e(n)应满足:
(4)

2.2 正弦载波产生电路的噪声分析
组成正弦载波产生电路的电子器件包括集成器件和电容、电阻为主的分立元件。
电阻的噪声主要是热噪声。热噪声起源于电阻内部电子的随机热运动,导致电阻两端电荷的瞬间堆积,形成噪声电压[5]。电阻的热噪声模型如图3所示[6]。
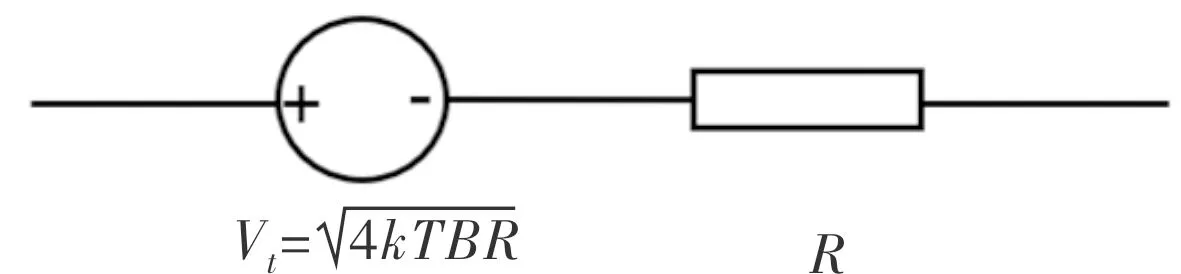
图3 电阻的噪声模型Fig.3 Noise model of resistor
其中,R是电阻,T是绝对温度,B是频率带宽,k是玻尔兹曼常数。
电容的热噪声主要由引线电阻和漏电阻产生,一般情况下电容的等效电阻很小,其产生的热噪声相较于电阻热噪声可以忽略[7]。
运算放大器在放大测量信号的同时放大了噪声,而且本身也会引入额外噪声。运算放大器内部包含大量晶体管,因此也存在大量的PN结,它们都是散弹噪声源;运算放大器的引脚及内部连接总会涉及不同金属的接触,1/f噪声必然存在。因此,运算放大器的噪声主要是由1/f噪声和白噪声混合而成的,在低频段主要是1/f噪声,在高频段主要是白噪声[5]。
运算放大器中的所有内部噪声源可折合到放大器的输入端,等效为3种输入噪声源:运算放大器的电压噪声en、运算放大器的电流噪声In和电路中电阻的热噪声eR,实际的运算放大器可以等效为二端口网络进行噪声研究,噪声模型如图4所示[8]。
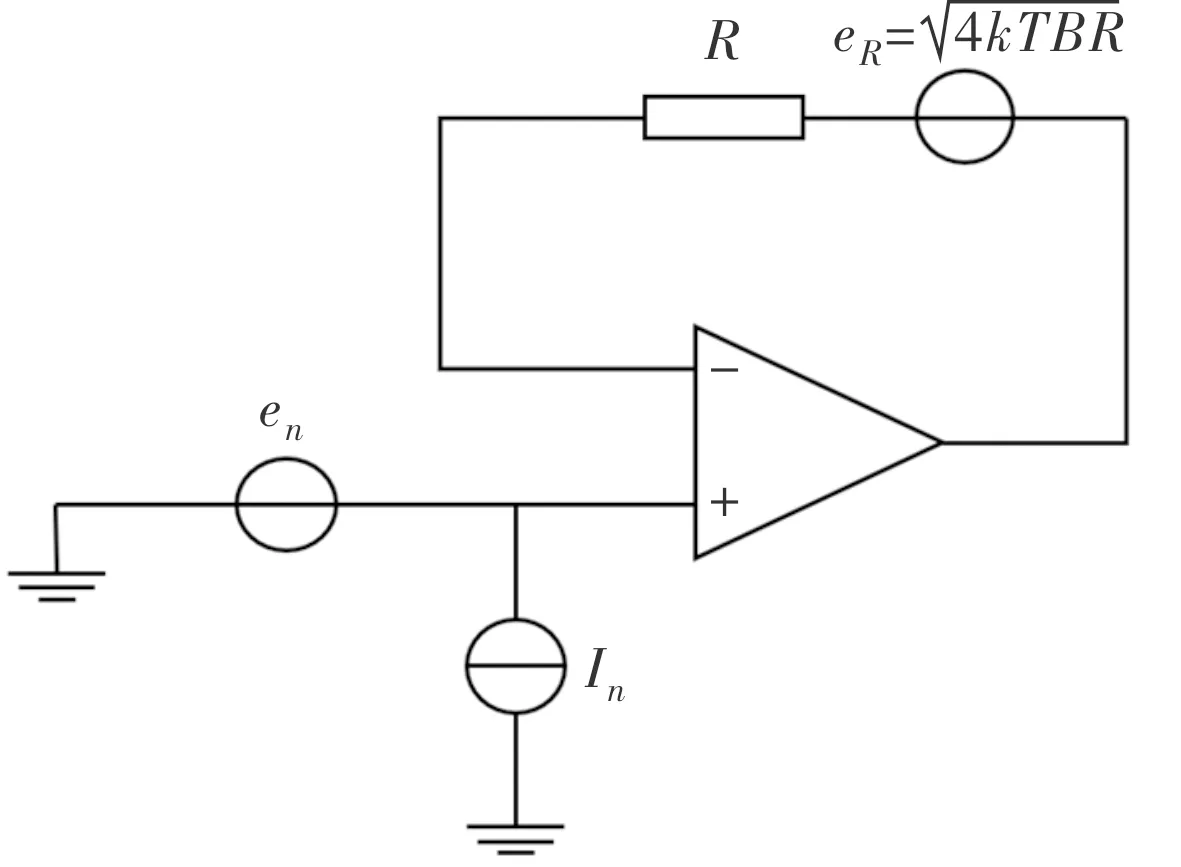
图4 运算放大器的噪声模型Fig.4 Noise model of operational amplifier
2.2.1 DAC及基准源噪声建模
本方案采用单芯片20位AD5791电压输出型数模转换器及LTC6655-5V电压基准源。AD5791采用精密电压模式R-2R架构,利用最新的薄膜电阻匹配技术,并通过片内校准例程实现1 ppm精度[9]。AD5791内部结构如图5所示[10]。

图5 AD5791内部架构Fig.5 Internal architecture of AD5791
AD5791所用精密架构要求使用高性能外置放大器来缓冲来自3.4kΩ DAC电阻的基准源,为基准输入引脚的加载感应提供方便,以确保AD5791的1 ppm的线性度。AD5791的外部基准电压源—LTC5566能实现在0.1~10 Hz范围内噪声低于1 μVp-p和小于2 ppm/℃的温度特性。
AD5791的理想传递函数为:
(5)
其中,VREFP是输入引脚上施加的正电压,VREFN是输入引脚上施加的负电压,D为写入DAC的20位代码。
对R-2R架构采用戴维宁定理[11]进行分析,得出AD5791内部等效电路如图6所示。考虑AD5791的内部噪声,得出等效噪声模型如图7所示。

图6 AD5791的内部等效电路Fig.6 Internal equivalent circuit of AD5791
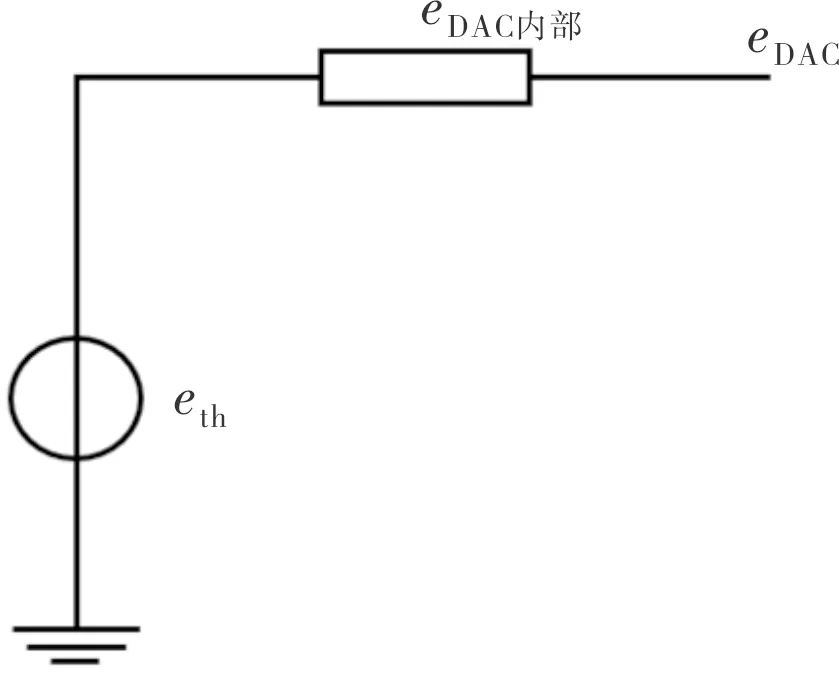
图7 AD5791的内部等效噪声模型Fig.7 Internal equivalent noise model of AD5791
由图7分析得知,AD5791的输出等效噪声为:
电压基准LTC6655通过AD5791影响正弦载波产生电路的性能,从而影响正弦载波的幅值稳定度。
已知AD5791及LTC6655手册中0.1~10 Hz频段内的频谱噪声图[12],文献[13]叙述的方法使用Origin软件进行非线性拟合得出研究频段1 mHz~10 Hz内的噪声密度图,如图8、图9所示。

图8 0.1~10 Hz频段内AD5791和LTC6655的频谱噪声图Fig.8 Spectral noise diagram of AD5791 and LTC6655 in 0.1~10 Hz frequency band

图9 1 mHz~10 Hz频段内的拟合电压噪声图Fig.9 Fitting voltage noise diagram in 1 mHz~10 Hz frequency band

2.2.2 正反相缓冲器噪声建模
本方案选用自动归零放大器LTC2057作为精密直流缓冲器,用于缓冲和反相AD5791输出结果。基于LTC2057运算放大器的缓冲电路噪声模型如图10所示。

图10 正相缓冲器的电路噪声模型Fig.10 Circuit noise model of positive phase buffer
图10中,en1是运放LTC2057的输入电压噪声源,In1是运放LTC2057的输入电流噪声源,eR1=R1·IR1、eR2=R2·IR2是电阻热噪声源。综合各个噪声源影响,得到正相缓冲器的输出电压噪声为:
(6)
已知LTC2057手册中0.1~100 Hz频段内的输入电压噪声图[14],文献[13]叙述的方法使用Origin进行非线性拟合可得出研究频段1 mHz~10 Hz内的噪声密度图,如图11所示。正反相缓冲器的输出电压噪声如图12所示。

图11 1 mHz~10 Hz频段内LTC2057的频谱噪声图Fig.11 Spectral noise diagram of LTC2057 in 1 mHz~10 Hz frequency band

图12 正反相缓冲器的输出电压噪声图Fig.12 Output voltage noise diagram of inverting buffer

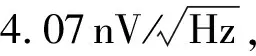

图13 电阻分压模型Fig.13 Resistance partial voltage model
2.2.3 多路复用器噪声分析
ADG506A是ADI公司中一种通用的多路16选1模拟开关,工作电压范围为10.8~16.5 V。ADG506A根据使能端EN和4位二进制地址端A0~A3的共同状态,从输入端S1~S16选通1路切送到公共输出端D,如图14所示[16]。
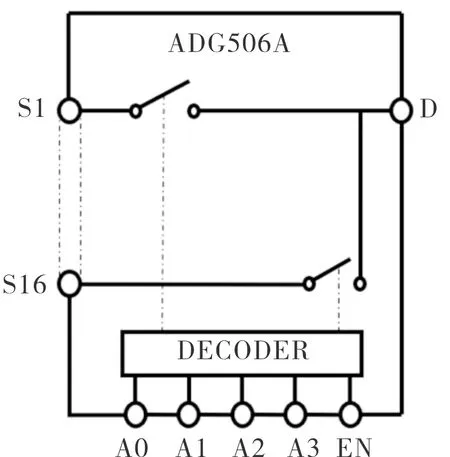
图14 ADG506的工作原理图Fig.14 Working principle diagram of ADG506
多路复用器中影响输出精度的因素主要有导通电阻RON、导通电容CON和漏电流ILEAKAGE。
导通电阻RON对数据信号的传输精度影响比较明显,且会随电源电压、传输信号幅度的变化而变化,即产生RON平面度,从而引入增益误差及线性误差。与多路复用器的导通电阻相比较,任何运放的输入阻抗都非常高,因此在模拟开关后可接入一个缓冲器,缓冲器的高输入阻抗将消除所有的增益误差以及因多路复用器RON和RON平面度产生的增益误差非线性。
一般来说,导通电阻低的模拟开关,其导通电容也低。因此,选用低导通电阻的ADG作为本方案中的多路复用器。高导通电容CON会与高导通电阻RON产生高时间常数,影响模拟开关的沉降时间,且有可能在输入通道快速切换的系统中导致失真。因此,更低的导通电阻会最大程度地减小增益相关误差;更低的导通电容有助于实现更快的沉降性能。
泄漏电流ILEAKAGE被指定为流经源引脚S和漏引脚D的电流。泄漏电流不管开关状态,都会造成直流误差,引起高输入阻抗系统出现偏移误差。泄漏电流与温度有关,在25 ℃~85 ℃范围内其值可近似不变[15],根据式(7)可知,泄漏电流在输入端造成的电压误差eADG与导通电阻RON有关,因此需选用导通电阻低的模拟开关。
eADG=(RON+Rsource)×ID(ON)
(7)
其中,eADG是泄漏电流在输入端造成的电压误差,RON是导通电阻,Rsource是源电阻,ID(ON)是开关打开时的泄漏电流。
基于25 ℃~85 ℃的温度范围,在模拟开关的分析中本文采用导通电阻的热噪声作为ADG506的输出噪声,如图15所示。
图15 ADG506导通电阻的热噪声Fig.15 Thermal noise of ADG506’s Ron
2.2.4 低通滤波器噪声建模
低通滤波器用于滤除高次谐波,本方案采用6阶低通滤波实现谐波滤除功能,单个低通滤波器基于ADA4625运算放大器构成的同相比例放大电路和二阶RC低通滤波组成,具有高输入阻抗、低输出阻抗等优点,根据载波要求截止至100 kHz,电路噪声模型如图16所示。

图16 单个低通滤波器的电路噪声模型Fig.16 Circuit noise model of a single low-pass filter
已知ADA4625手册中0.1~100 Hz频段内的输入电压噪声图[17],参考文献[13]中叙述的方法使用Origin进行非线性拟合得出研究频段1 mHz~10 Hz内的噪声密度图,如图17所示。参考2.2.2噪声模型分析,得到低通滤波器的输出电压噪声如图18所示。

图17 ADA4625的拟合电压噪声频谱图Fig.17 A fitting voltage-noise spectrum diagram for ADA4625

图18 低通滤波器的输出电压噪声图Fig.18 Output voltage noise diagram of low-pass filter

2.3 结果分析
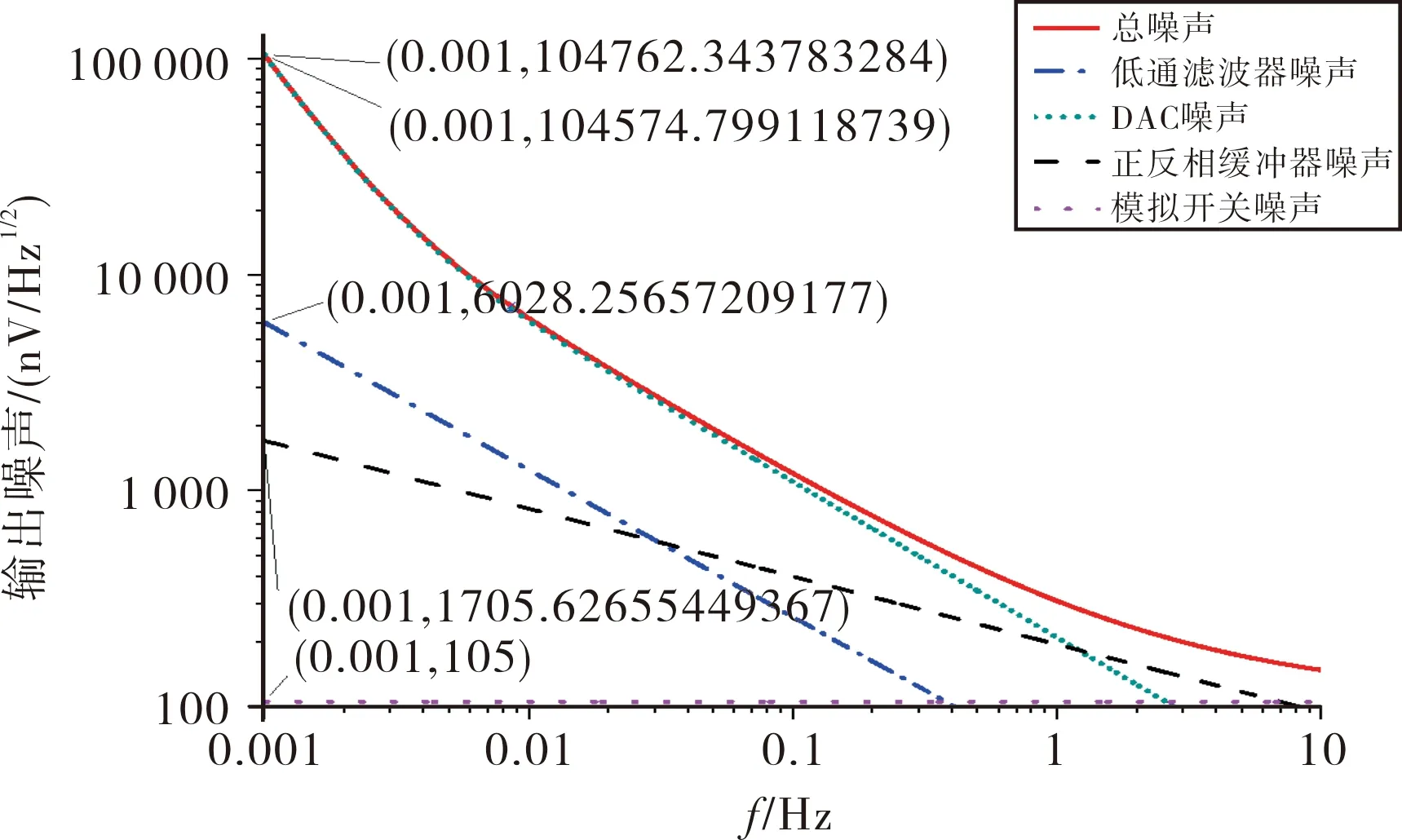
图19 电压噪声分布图Fig.19 Voltage noise distribution
3 结论
本文通过对电路设计及噪声理论分析,研究了正弦载波的产生电路及波形幅值稳定度,得出以下结论:

2)基于DDS产生正弦载波的基本原理,本方案将影响波形幅值稳定度的相关因素进行改良,输出具有高幅值稳定度的正弦载波。根据噪声总体分布图19所示,基于DDS基本原理进行改良的阶梯波滤波电路的噪声主要来源于基准电压源;
3)本文进行的噪声机理研究是在不考虑器件温漂的前提下进行,若考虑温度影响,本方案所得出的正弦载波幅值稳定度会有所变化;
4)本文主要研究正弦载波幅值稳定度的影响因素,未考虑载波频率稳定度,这可能会对后续解调器造成影响。
为使本文提出的设计方案能输出具有更高幅值稳定度的正弦载波及相关电路应用,后续研究将针对基准电压源、温度及频率稳定度等因素进行详细分析,并对该方案进行实际电路验证。
